42 câu Trắc nghiệm Hàm số bậc nhất và đồ thị của hàm số bậc nhất (Kết nối tri thức 2024) có đáp án

42 câu Trắc nghiệm Hàm số bậc nhất và đồ thị của hàm số bậc nhất (Kết nối tri thức 2024) có đáp án - Toán lớp 8

Van Anh Ngày: 03-01-2024 Lớp 8

3.9 K

Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất sách Kết nối tri thức. Bài viết gồm 43 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 8.

Trắc nghiệm Toán 8 Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Câu 1 : Cho hàm số $y = (m - 1) x + m^{2}$ . Có bao nhiêu giá trị của m để hàm số đã cho là hàm số không là hàm số bậc nhất?

A
Không có giá trị nào
B
1 giá trị
C
2 giá trị
D
Vô số giá trị

Đáp án : B

Lời giải :

Để hàm số $y = (m - 1) x + m^{2}$ là hàm số bậc nhất thì $m - 1 \neq 0$

$m \neq 1$

Do đó, hàm số $y = (m - 1) x + m^{2}$ là hàm số bậc nhất khi $m \neq 1$

Vậy có 1 giá trị của m để hàm số $y = (m - 1) x + m^{2}$ không là hàm số bậc nhất là $m = 1$

Câu 2 : Cho hàm số bậc nhất $y = \frac{- 1}{5} x + 7.$ Điểm nào dưới đây thuộc hàm số đã cho?

A
A(7; 0)
B
B(-7; 0)
C
C(0; 7)
D
$D (\frac{1}{7}; 0)$

Đáp án : C

Lời giải:

Với $x = 0$ ta có $y = \frac{- 1}{5} .0 + 7 = 7$

Do đó, điểm C(0; 7) thuộc hàm số bậc nhất $y = \frac{- 1}{5} x + 7.$

Các điểm còn lại thay tọa độ vào đều không thuộc hàm số bậc nhất $y = \frac{- 1}{5} x + 7.$

Câu 3 : Cho hàm số bậc nhất $y = 2 x + b .$ Biết rằng điểm M(2; 4) thuộc hàm số trên.

Chọn khẳng định đúng?

A
$b = 0$
B
$b = 1$
C
$b = 2$
D
$b = - 1$

Đáp án : A

Lời giải :

Vì điểm M(2; 4) thuộc hàm số trên nên $x = 2; y = 4,$ thay vào hàm số $y = 2 x + b$ ta có:

$4 = 2.2 + b$

$4 = 4 + b$

$b = 0$

Câu 4 : Với giá trị nào của m thì hàm số $y = 3 m x + 6 m - x$ là hàm số bậc nhất?

A
$m \neq - 3$
B
$m \neq 3$
C
$m \neq \frac{- 1}{3}$
D
$m \neq \frac{1}{3}$

Đáp án : D

Lời giải :

Ta có: $y = 3 m x + 6 m - x = (3 m - 1) x + 6 m$

Để hàm số $y = (3 m - 1) x + 6 m$ là hàm số bậc nhất thì:

$3 m - 1 \neq 0$

$3 m \neq 1$

$m \neq \frac{1}{3}$

Câu 5 : Cho hàm số bậc nhất $y = a x + 1 (a \neq 0) .$ Biết rằng điểm A(1; 7) thuộc hàm số trên.

Trong các điểm M(2; 13), N(13; 2), P(6;0), có bao nhiêu điểm thuộc hàm số trên.

A
0 điểm
B
1 điểm
C
2 điểm
D
3 điểm

Đáp án : B

Lời giải :

Vì điểm A(1; 7) thuộc hàm số trên nên $7 = a .1 + 1$

$a = 7 - 1 = 6$ (thỏa mãn)

Do đó, hàm số cần tìm là $y = 6 x + 1$

Thay tọa độ các điểm M, N, P vào hàm số trên thì ta thấy chỉ có điểm M(2; 13) thuộc hàm số

$y = 6 x + 1$

Vậy có 1 điểm trong 3 điểm M, N, P thuộc hàm số.

Câu 6 : Chọn khẳng định đúng.

A
Hàm số bậc nhất có dạng $y = a x + b$ , trong đó a, b là các số cho trước
B
Hàm số bậc nhất có dạng $y = a x + b$ , trong đó a, b là các số cho trước và a khác 0
C
Hàm số bậc nhất có dạng $y = a x + b$ , trong đó a, b là các số cho trước và b khác 0
D
Hàm số bậc nhất có dạng $y = a x + b$ , trong đó a, b là các số cho trước và a, b khác 0

Đáp án : B

Lời giải :

Hàm số bậc nhất có dạng

y = a x + b

, trong đó a, b là các số cho trước và a khác 0

Câu 7 : Cho hàm số bậc nhất $y = 2 x + 1,$ biết rằng a, b lần lượt là hệ số của x và hệ số tự do. Khi đó:

A
$a = 2; b = 1$
B
$a = 1; b = 2$
C
$a = 2; b = 0$
D
$a = 0; b = 2$

Đáp án : A

Lời giải :

Hàm số

y = 2 x + 1

có

a = 2; b = 1

Câu 8 : Trong các hàm số sau, hàm số nào không là hàm số bậc nhất?

A
$y = 2 x$
B
$y = 1$
C
$y = \frac{- 1}{2} x + 4$
D
$y = - 6 x + 1$

Đáp án : B

Lời giải :

Hàm số không là hàm số bậc nhất là:

y = 1

vì hệ số của x bằng 0.

Câu 9 : Cho hàm số bậc nhất $y = \frac{1}{3} x + 6$ , giá trị của y tương ứng với $x = 3$ là:

A
$y = 5$
B
$y = 7$
C
$y = 6$
D
$y = 8$

Đáp án : B

Lời giải :

Với $x = 3$ ta có: $y = 3. \frac{1}{3} + 6 = 1 + 6 = 7$

Câu 10 : Giá bán 1kg vải thiều loại I là 40 000 đồng.

Chọn đáp án đúng.

A
Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là $y = 40 000 x$ , y là hàm số bậc nhất của x.
B
Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là $y = 40 000 x$ , y không là hàm số bậc nhất của x.
C
Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là $x = 40 000 y$ , y không là hàm số bậc nhất của x.
D
Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là $x = 40 000 y$ , y là hàm số bậc nhất của x.

Đáp án : A

Lời giải :

Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là $y = 40 000 x$ , y là hàm số bậc nhất của x.

Câu 11 : Một hình chữ nhật có các kích thước là 2m và 3m. Gọi y là chu vi của hình chữ nhật này sau khi tăng chiều dài và chiều rộng thêm x(m).

Chọn đáp án đúng.

A
$y = 4 x + 10$ không là hàm số bậc nhất theo biến số x.
B
$y = 4 x + 10$ là hàm số bậc nhất theo biến số x.
C
$y = 2 x + 5$ là hàm số bậc nhất theo biến số x.
D
$y = 2 x + 5$ không là hàm số bậc nhất theo biến số x.

Đáp án : B

Lời giải :

Chiều dài sau khi tăng x(m) là: $x + 2 (m)$

Chiều rộng sau khi tăng x(m) là: $x + 3 (m)$

Chu vi của hình chữ nhật mới là: $y = 2 (x + 2 + x + 3) = 2 (2 x + 5) = 4 x + 10$

Do đó, $y = 4 x + 10$ là hàm số bậc nhất theo biến số x.

Câu 12 : Hiện tại bạn An đã để dành được 400 000 đồng. Bạn An đang có ý định mua một chiếc xe đạp giá 2 000 0000 đồng. Để thực hiện được điều trên, bạn An đã lên kế hoạch mỗi ngày đều tiết kiệm 10 000 đồng. Gọi m (đồng) là số tiền bạn An tiết kiệm được sau t ngày.

Cho khẳng định sau:

Khẳng định 1: m là hàm số bậc nhất của t.

Khẳng định 2: Sau 4 ngày kể từ ngày An bắt đầu tiết kiệm, bạn tiết kiệm được 30 000 đồng

Khẳng định 3: Sau 150 ngày kể từ ngày bắt đầu tiết kiệm, An có thể mua được chiếc xe đạp đó.

Số khẳng định đúng là?

A
0.
B
1.
C
2.
D
3.

Đáp án : B

Lời giải :

+ Số tiền An tiết kiệm được sau t ngày là: $m = 10 000 t$ , do đó m là hàm số bậc nhất của t.

+ Sau 4 ngày kể từ ngày bắt đầu tiết kiệm, An tiết kiệm được số tiền là: $m = 4.10 000 = 40 000$ (đồng)

+ An còn thiếu số tiền là: $2 000 000 - 400 000 = 1 600 000$ (đồng) nên $m = 1 600 000$

Ta có: $1 600 000 = m .10 000$ $\Rightarrow$ $m = 160$ (ngày)

Do đó, sau 160 ngày kể từ ngày tiết kiệm, An có thể mua được xe đạp đó.

Vậy trong 3 khẳng định trên, có 1 khẳng định đúng.

Câu 13 : Bạn D mang theo 100 000 đồng và đạp xe đi nhà sách để mua vở. Biết giá mỗi quyển vở là 6000 đồng, phí gửi xe là 5 000 đồng.

Chọn khẳng định đúng.

A
Công thức biểu thị tổng số tiền D cần trả cho việc gửi xe đạp và mua x quyển vở là $y = 5 000 + 6 000 x$ (đồng), y là hàm số bậc nhất của x.
B
Công thức biểu thị tổng số tiền D cần trả cho việc gửi xe đạp và mua x quyển vở là $y = 5 000 + 6 000 x$ (đồng), y không là hàm số bậc nhất x.
C
Với số tiền D mang đi, D có thể mua được 17 quyển vở sau khi trả tiền gửi xe.
D
Với số tiền D mang đi, D có thể mua được 16 quyển vở sau khi trả tiền gửi xe.

Đáp án : A

Lời giải :

Giá tiền mua x quyển vở là $6 000 x$ (đồng)

Công thức biểu thị tổng số tiền D cần trả cho việc gửi xe đạp và mua x quyển vở là $y = 5 000 + 6 000 x$ (đồng), do đó, y là hàm số bậc nhất của x

Số tiền phải trả khi trả tiền xe và mua 16 quyển vở là: $y = 5 000 + 6 000.16 = 101 000$ (đồng)

Vì $101 000 > 100 000$ nên D không thể mua được 16 quyển vở sau khi trả tiền gửi xe, do đó, D cũng không thể mua được 17 quyển vở.

Câu 14 : Cho hàm số bậc nhất $y = a x + b (a \neq 0) .$ Biết rằng điểm A(0;1) và điểm B(2; 6) thuộc hàm số trên. Khi đó, hàm số bậc nhất là:

A
$y = x + \frac{2}{5}$
B
$y = \frac{2}{5} x + 1$
C
$y = x + \frac{5}{2}$
D
$y = \frac{5}{2} x + 1$

Đáp án : D

Lời giải :

Vì A(0;1) thuộc đồ thị hàm số nên $1 = 0. a + b$ , tìm được $b = 1$

Hàm số: $y = a x + 1$

Vì điểm B(2; 6) thuộc hàm số trên nên $6 = 2. a + 1$

$2 a = 5$

$a = \frac{5}{2}$ (thỏa mãn)

Vậy hàm số cần tìm là: $y = \frac{5}{2} x + 1$

Câu 15 : Một người đang sử dụng Internet, mỗi phút tốn dung lượng 1MB. Giả sử gói cước Internet của người đó cho phép sử dụng dung lượng 5MB

Chọn đáp án đúng.

A
Hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng internet x (giây) là $y = 60 x$
B
Hàm số g(x) biểu thị dung lượng cho phép còn lại (MB) sau khi sử dụng internet được x (giây) là $g (x) = 5 - 60 x$
C
Sau khi sử dụng internet 2 phút thì dung lượng cho phép còn lại là 3MB
D
Sau khi sử dụng internet 2 phút thì dung lượng cho phép còn lại là 2MB

Đáp án : C

Lời giải :

Đổi 1 phút $= 60$ giây

Mỗi phút tốn dung lượng 1MB nên mỗi giây tốn $\frac{1}{60} M B$

Hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng internet x (giây) là $y = \frac{1}{60} x$

Hàm số g(x) biểu thị dung lượng cho phép còn lại (MB) sau khi sử dụng internet được x (giây) là $g (x) = 5 - \frac{1}{60} x$

Sau khi sử dụng internet 2 phút $= 120$ giây thì dung lượng cho phép còn lại là:

$g (120) = 5 - \frac{120}{60} = 3 (M B)$

Câu 16 : Cho hàm số bậc nhất $y = m x + m + 1 (m \neq 0)$ , biết rằng điểm A(0; 3) thuộc hàm số đã cho. Nếu điểm M có hoành độ là 6 thuộc hàm số trên thì tọa độ của điểm M là:

A
M(6; 15)
B
M(15; -6)
C
M(-6; 15)
D
M(15; 6)

Đáp án : A

Lời giải :

Vì A(0; 3) thuộc đồ hàm số đã cho nên $3 = 0. m + m + 1$

$m = 2$

Khi đó, ta có hàm số: $y = 2 x + 3$

Với $x = 6$ ta có: $y = 2.6 + 3 = 15$

Do đó M(6; 15) thuộc hàm số $y = 2 x + 3$

Câu 17 : Cho hàm số $2 y + 4 x + 6 = 0 (1)$ . Trong các khẳng định:

Khẳng định 1: Hàm số (1) là hàm số bậc nhất

Khẳng định 2: Điểm thuộc trục tung có tung độ bằng 4 thuộc hàm số (1)

Khẳng định 3: Điểm thuộc trục hoành có hoành độ bằng 4 thuộc hàm số (1)

Số khẳng định sai là:

Đáp án : C

Lời giải :

Ta có: $2 y + 4 x + 6 = 0$

$y + 2 x + 3 = 0$

$y = - 2 x - 3$

Với $x = 0$ thì $y = - 3$ nên điểm thuộc trục tung có tung độ bằng -3 thuộc hàm số (1)

Với $y = 0$ thì $x = \frac{- 3}{2}$ nên điểm thuộc trục hoành có hoành độ bằng $\frac{- 3}{2}$ thuộc hàm số (1)

Do đó, trong các khẳng định trên có 2 khẳng định sai.

Câu 18 : Cho hàm số $y = \sqrt{2} (x - 1) + 2 x + 1 (1) .$ Cho các khẳng định:

(1) Hàm số (1) là hàm số bậc nhất

(2) Điểm A(0; 1) thuộc hàm số (1)

(3) Giá trị của hàm số tại $x = 1$ là 3

Hỏi có bao nhiêu khẳng định đúng?

Đáp án : C

Lời giải :

Ta có: $y = \sqrt{2} (x - 1) + 2 x + 1 = \sqrt{2} x - \sqrt{2} + 2 x + 1 = (\sqrt{2} + 2) x + 1 - \sqrt{2}$

Do đó, hàm số đã cho là hàm số bậc nhất.

Với $x = 0$ thì $y = 1 - \sqrt{2}$ do đó, điểm A(0; 1) không thuộc hàm số (1)

Với $x = 1$ ta có: $y = \sqrt{2} (1 - 1) + 2.1 + 1 = 3$

Do đó, có 2 khẳng định đúng.

Câu 19 : Cho hàm số bậc nhất $y = (2 m - 1) x + m^{2} + 2 (1) .$ Biết điểm A thuộc trục hoành có hoành độ bằng 1 thuộc hàm số trên. Khi đó,

A
$m = 2$
B
$m = 0$
C
$m = 1$
D
$m = - 1$

Đáp án : D

Lời giải:

Để (1) là hàm số bậc nhất thì $m \neq \frac{1}{2}$

Vì điểm A thuộc trục hoành và có hoành độ bằng 1 nên $x = 1; y = 0$

Do đó, $0 = (2 m - 1) .1 + m^{2} + 2 = m^{2} + 2 m + 1 = {(m + 1)}^{2}$

$m + 1 = 0$

$m = - 1$ (thỏa mãn)

Câu 20 : : Cho hàm số $y = (a^{2} - 4) x^{2} + (b - 3 a) (b + 2 a) x - 2$ là hàm số bậc nhất khi:

A
$a = 2; b \neq {6; - 4}$
B
$a = - 2; b \neq {- 6; 4}$
C
$a = 2; b = - 2$
D
Cả A, B, C đều đúng

Đáp án : D

Lời giải :

Hàm số $y = (a^{2} - 4) x^{2} + (b - 3 a) (b + 2 a) x - 2$ là hàm số bậc nhất khi $a^{2} - 4 = 0$ và $(b - 3 a) (b + 2 a) \neq 0$

+) $a^{2} - 4 = 0$

$a^{2} = 4$

$a = \pm 2$

+) $(b - 3 a) (b + 2 a) \neq 0$

${\begin{cases} b \neq 3 a \\ b \neq - 2 a \end{cases}$

Với $a = 2$ thì ${\begin{cases} b \neq 6 \\ b \neq - 4 \end{cases}$

Với $a = - 2$ thì ${\begin{cases} b \neq - 6 \\ b \neq 4 \end{cases}$

Câu 21 : Cho hai điểm $A (x_{1}; y_{1}), B (x_{2}; y_{2})$ với $x_{1} \neq x_{2}; y_{1} \neq y_{2} .$ Nếu hai điểm A, B thuộc hàm số $y = a x + b$ thì:

A
$\frac{y - y_{1}}{y_{2} - y_{1}} = 2 \frac{x - x_{1}}{x_{2} - x_{1}}$
B
$\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2} - x_{1}}$
C
$2 \frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2} - x_{1}}$
D
$\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{- x - x_{1}}{x_{2} - x_{1}}$

Đáp án : B

Lời giải:

Vì $A (x_{1}; y_{1})$ thuộc hàm số $y = a x + b$ nên $y_{1} = a x_{1} + b$ , suy ra $y - y_{1} = a (x - x_{1})$ (1)

Vì $B (x_{2}; y_{2})$ thuộc hàm số $y = a x + b$ nên $y_{2} = a x_{2} + b$ , suy ra $y_{2} - y_{1} = a (x_{2} - x_{1})$ (2)

Từ (1) và (2) ta có: $\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2} - x_{1}}$

Câu 22 : Cho hai hàm số: $y = (2 m + m^{2} + 6) x + m^{5} + 8 (1)$ và $y = (- 2 m^{4} + 8 m^{2} - 12) x + m^{10} - 6 m^{5} (2)$

Có bao nhiêu giá trị của m để cả hai hàm số trên không là hàm số bậc nhất.

Đáp án : A

Lời giải :

Hàm số (1) là hàm số bậc nhất khi $2 m + m^{2} + 6 \neq 0$

Mà $m^{2} + 2 m + 6 = m^{2} + 2 m + 1 + 5 = {(m + 1)}^{2} + 5 > 0$ với mọi giá trị của m

Do đó, hàm số (1) luôn là hàm số bậc nhất với mọi giá trị của m.

Hàm số (2) là hàm số bậc nhất khi $- 2 m^{4} + 8 m^{2} - 20 \neq 0$

Mà $- 2 m^{4} + 8 m^{2} - 20 = - 2 (m^{4} - 4 m^{2} + 4) - 4 = - 2 {(m^{2} - 2)}^{2} - 4 < 0$ với mọi giá trị của m

Do đó, hàm số (2) là hàm số bậc nhất với mọi giá trị của m.

Vậy không có giá trị của m để cả 2 hàm số trên không là hàm số bậc nhất.

Câu 23 : Trong các hình vẽ dưới đây, hình vẽ nào là đồ thị của hàm số $y = 1 + 2 x$ ?

A
Hình 4
B
Hình 1
C
Hình 2
D
Hình 3

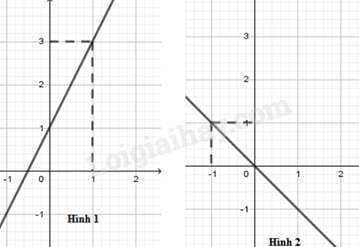
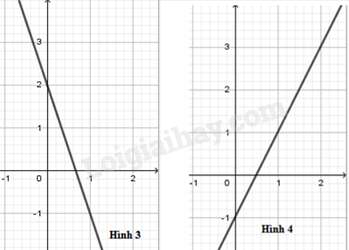
Đáp án : B

Lời giải :

Đồ thị của hàm số $y = 1 + 2 x$ đi qua các điểm có tọa độ (0; 1) và $(\frac{- 1}{2}; 0)$ nên hình 1 là đồ thị của hàm số $y = 1 + 2 x$

Câu 24 : Cho đồ thị hàm số $y = x + 1.$ Điểm nào dưới đây thuộc đồ thị hàm số trên?

A
O(0; 0)
B
A(-1; 1)
C
B(-1; -1)
D
C(-1; 0)

Đáp án : D

Lời giải :

Với x = 0, ta có y = 0 + 1 = 1 nên O(0; 0) không thuộc đồ thị hàm số y = x + 1.

Với x = -1, ta có y = -1 + 1 = 0 nên điểm C(-1; 0) thuộc đồ thị hàm số $y = x + 1$ .

Câu 25 : Một người đi bộ trên đường thẳng với vận tốc v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ). Khi đó, đồ thị của hàm số s theo biến t với $v = 5$ đường thẳng nào trong hình vẽ dưới đây?

A
Đường thẳng p
B
Đường thẳng EA
C
Trục Ox
D
Đường thẳng q

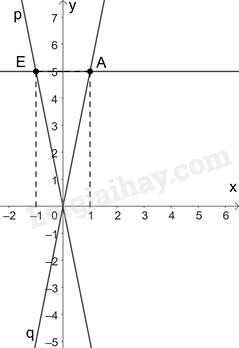
Đáp án : D

Lời giải :

Hàm số s theo biến t với $v = 5$ là: $s = 5 t$

Đồ thị hàm số $s = 5 t$ đi qua 2 điểm O(0; 0) và A(1; 5)

Do đó, đồ thị hàm số $s = 5 t$ là đường thẳng q.

Câu 26 : Cho đường thẳng d: $y = 2 x + m .$ Đường thẳng d đi qua điểm A(1; 5). Chọn đáp án đúng.

A
$m = - 2$
B
$m = 2$
C
$m = 3$
D
$m = - 1$

Đáp án : C

Lời giải:

Đường thẳng d đi qua điểm A(1; 5) nên $5 = 2.1 + m$

$m = 3$

Câu 27 : Cho hàm số bậc nhất $y = (2 - m) x + m$ . Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ 4.

A
$m = \frac{8}{3}$
B
$m = \frac{- 8}{3}$
C
$m = \frac{3}{8}$
D
$m = \frac{- 3}{8}$

Đáp án : A

Lời giải :

Hàm số $y = (2 - m) x + m$ là hàm số bậc nhất khi $m \neq 2$

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 4 nên $x = 4; y = 0$

Do đó, $0 = 4 (2 - m) + m$

$8 - 4 m + m = 0$

$3 m = 8$

$m = \frac{8}{3}$ (thỏa mãn)

Câu 28 : Đồ thị của hàm số $y = a x + b (a \neq 0)$ là:

A
Một đường thẳng
B
Một đường tròn
C
Một đường cong
D
Một đường gấp khúc

Đáp án : A

Lời giải :

Đồ thị của hàm số

y = a x + b (a \neq 0)

là một đường thẳng.

Câu 29 : Đồ thị hàm số $y = a x + b (a \neq 0)$ là một đường thẳng cắt trục tung tại điểm có tung độ bằng:

A
a
B
$\frac{a}{b}$
C
b
D
$\frac{- b}{a}$

Đáp án : C

Lời giải :

Đồ thị hàm số

y = a x + b (a \neq 0)

là một đường thẳng cắt trục tung tại điểm có tung độ bằng b.

Câu 30 : Cho hai đường thẳng $d_{1} : y = x - 1$ và $d_{2} : y = 3 - 4 x .$ Tung độ giao điểm của hai đường thẳng $d_{1}$ và $d_{2}$ là:

A
$- 5$
B
$5$
C
$\frac{1}{5}$
D
$\frac{- 1}{5}$

Đáp án : D

Lời giải :

Xét phương trình hoành độ giao điểm của $d_{1}$ và $d_{2}$ :

$x - 1 = 3 - 4 x$

$5 x = 4$

$x = \frac{4}{5}$

Với $x = \frac{4}{5}$ thì $y = \frac{4}{5} - 1 = \frac{- 1}{5}$

Vậy tung độ giao điểm của hai đường thẳng $d_{1}$ và $d_{2}$ là $\frac{- 1}{5}$

Câu 31 : Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ: $y = x; y = x + 2;$ $y = - x + 2; y = - x .$ Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì?

A
Hình thoi
B
Hình chữ nhật
C
Hình vuông
D
A, B, C đều sai.

Đáp án : A

Lời giải :

Với hàm số y = x, cho x = 1 thì y = 1. Đồ thị hàm số y = x đi qua các điểm O(0;0) và C(1;1)

Với hàm số y = x+2, cho x = 0 thì y = 2, cho x = -1 thì y = 1. Đồ thị hàm số y = x +2 đi qua các điểm B(0;2) và A(-1;1)

Với hàm số y = -x, cho x = -1 thì y = 1. Đồ thị hàm số y = -x đi qua các điểm O(0;0) và A(-1;1)

Với hàm số y = -x +2, cho x =0 thì y = 2, cho x = 1 thì y = 1. Đồ thị hàm số y = -x +2 đi qua các điểm B (0;2) và C(1;1)

Đồ thị hàm số:

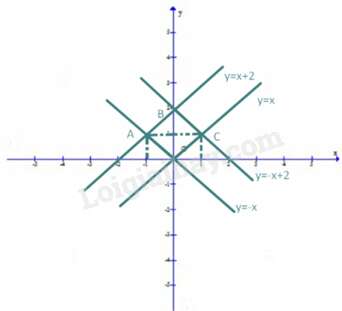
Từ đồ thị trên ta thấy:

Đường thẳng $y = x$ song song với đường thẳng $y = x + 2$ nên OC//AB

Đường thẳng $y = - x$ song song với đường thẳng $y = - x + 2$ nên OA//BC

Tứ giá OABC có: OC//AB, OA//BC và $O B ⊥ A C$ nên tứ giác OABC là hình thoi

Câu 32 : Cho hàm số $y = m x + 2$ có đồ thị là đường thẳng $d_{1}$ và hàm số $y = \frac{1}{2} x + 1$ có đồ thị là đường thẳng $d_{2} .$ Để đường thẳng $d_{1}$ và đường thẳng $d_{2}$ cắt nhau tại một điểm có hoành độ bằng 4 là:

A
$m = - \frac{1}{4}$
B
$m = \frac{1}{4}$
C
$m = 4$
D
$m = - 4$

Đáp án : B

Lời giải :

Phương trình hoành độ giao điểm của $d_{1}$ và $d_{2}$ là: $m x + 2 = \frac{1}{2} x + 1$ (1)

Để đường thẳng $d_{1}$ và đường thẳng $d_{2}$ cắt nhau tại một điểm có hoành độ bằng 4 thì $x = 4$ thỏa mãn phương trình (*). Do đó, $4 m + 2 = \frac{1}{2} .4 + 1$

$4 m = 1$

$m = \frac{1}{4}$

Câu 33 : Cho hàm số $y = (m - 1) x - 1$ có đồ thị là đường thẳng $d_{1}$ và hàm số $y = x + 1$ có đồ thị là đường thẳng $d_{2} .$ Để đường thẳng $d_{1}$ và đường thẳng $d_{2}$ cắt nhau tại một điểm có tung độ bằng 4 là:

A
$m = 8$
B
$m = \frac{8}{3}$
C
$m = \frac{3}{8}$
D
$m = 3$

Đáp án : B

Lời giải:

Để đường thẳng $d_{1}$ và đường thẳng $d_{2}$ cắt nhau tại một điểm có tung độ bằng 4 nên thay $y = 4$ vào $y = x + 1$ ta có: $4 = x + 1$ , $x = 3$

Do đó, tọa độ giao điểm của $d_{1}$ và $d_{2}$ là $(3; 4)$

Thay $x = 3, y = 4$ vào $y = (m - 1) x - 1$ ta có:

$4 = 3 (m - 1) - 1$

$3 m - 3 - 1 = 4$

$m = \frac{8}{3}$

Câu 34 : Cho đường thẳng $d_{1} : y = - x + 3$ và $d_{2} : y = 4 - 3 x .$ Gọi A và B lần lượt là giao điểm của $d_{1}$ và $d_{2}$ với trục hoành. Tổng hoành độ giao điểm của hai điểm A và B là:

A
$\frac{6}{13}$
B
$\frac{3}{13}$
C
$\frac{13}{3}$
D
$\frac{13}{6}$

Đáp án : C

Lời giải :

Đường thẳng $d_{1}$ cắt trục hoành tại điểm A nên A có tung độ $y = 0.$ Do đó, $0 = - x + 3; x = 3$ nên hoành độ của điểm A là $x = 3$

Đường thẳng $d_{2}$ cắt trục hoành tại điểm B nên B có tung độ $y = 0.$ Do đó, $0 = 4 - 3 x; x = \frac{4}{3}$ nên hoành độ của điểm B là $x = \frac{4}{3}$

Do đó, tổng hoành độ giao điểm của A và B là $\frac{13}{3}$

Câu 35 : Cho đường thẳng d: $y = - 2 x - 4.$ Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là:

A
4đvdt
B
3đvdt
C
2đvdt
D
1đvdt

Đáp án : A

Lời giải :

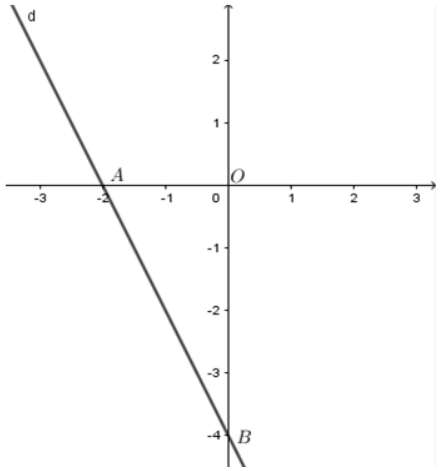
A là giao điểm của d với trục hoành nên $0 = - 2 x - 4, x = - 2$ nên $A (- 2; 0)$

B là giao điểm của d với trục tung nên $y = - 2.0 - 4 = - 4$ nên $B (0; - 4)$

Do đó, $O A = 2, O B = 4$

Vì tam giác AOB vuông tại O nên diện tích tam giác OAB là: $S = \frac{O A . O B}{2} = \frac{2.4}{2} = 4$ (đvdt)

Câu 36 : Với giá trị nào của m thì ba đường thẳng $d_{1} : y = (m - 1) x - 3; d_{2} : y = 2 x + 1; d_{3} : y = x - 3$ giao nhau tại một điểm?

A
$m = - 1$
B
$m = 1$
C
$m = 2$
D
$m = - 2$

Đáp án : C

Lời giải :

Xét phương trình hoành độ giao điểm của $d_{2}$ và $d_{3}$ :

$2 x + 1 = x - 3$

$x = - 4$

Với $x = - 4$ vào $y = x - 3$ ta có: $y = - 4 - 3 = - 7$

Do đó, giao điểm của $d_{2}$ và $d_{3}$ là M(-4; -7)

Để ba đường thẳng $d_{1} : y = (m - 1) x - 3; d_{2} : y = 2 x + 1; d_{3} : y = x - 3$ giao nhau tại một điểm thì M thuộc $d_{1} .$ Do đó,

$- 7 = - 4 (m - 1) - 3$

$- 4 m + 4 - 3 = - 7$

$- 4 m = - 8$

$m = 2$

Câu 37 : Gọi $d_{1}$ là đồ thị của hàm số $y = m x - 1$ và $d_{2}$ là đồ thị hàm số $y = \frac{1}{2} x + 2$ . Để M(2; 3) là giao điểm của $d_{1}$ và $d_{2}$ thì giá trị của m là:

A
$m = - 1$
B
$m = 1$
C
$m = 2$
D
$m = - 2$

Đáp án : C

Lời giải :

+ Nhận thấy M thuộc $d_{2}$

Thay tọa độ M vào $y = m x - 1$ ta có:

$3 = m .2 - 1$

$2 m = 4$

$m = 2$

Câu 38 : Cho đường thẳng d được xác định bởi $y = 2 x + 10.$ Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành là:

A
$y = - 2 x + 10$
B
$y = - 2 x - 10$
C
$y = 2 x - 10$
D
Đáp án khác

Đáp án : B

Lời giải :

Điểm đối xứng với điểm (x; y) qua trục hoành là điểm (x; -y)

Xét hàm số $y = 2 x + 10,$ thay y bởi $- y$ ta được: $- y = 2 x + 10$ hay $y = - 2 x - 10$

Câu 39 : Cho đường thẳng d xác định bởi $y = 2 x + 4.$ Đường thẳng d’ đối xứng với đường thẳng d qua đường thẳng $y = x$ là:

A
$y = \frac{1}{2} x + 2$
B
$y = x - 2$
C
$y = \frac{1}{2} x - 2$
D
$y = - 2 x - 4$

Đáp án : C

Lời giải :

Điểm đối xứng với điểm (x; y) qua đường thẳng $y = x$ là $(y; x)$

Xét hàm số, $y = 2 x + 4,$ thay x bởi y, thay y bởi x ta có: $x = 2 y + 4$ hay $y = \frac{1}{2} x - 2$

Câu 40 : : Cho đường thẳng $y = m x + m + 1 (1)$ (m là tham số). Đường thẳng (1) luôn đi qua một điểm cố định mới mọi giá trị của m. Điểm cố định đó là:

A
(1; -1)
B
(1; 1)
C
(-1; -1)
D
(-1; 1)

Đáp án : D

Lời giải :

Gọi điểm $N (x_{0}; y_{0})$ là điểm cố định của đường thẳng (1).

Ta có: $y_{0} = m x_{0} + m + 1$

$y_{0} - m x_{0} - m - 1 = 0$

$- (x_{0} + 1) m + y_{0} - 1 = 0$

${\begin{cases} x_{0} + 1 = 0 \\ y_{0} - 1 = 0 \end{cases}$ ${\begin{cases} x_{0} = - 1 \\ y_{0} = 1 \end{cases}$

Vậy đường thẳng (1) luôn đi qua điểm cố định (-1; 1).

Câu 41 : Tìm x sao cho ba điểm A(x; 14), B(-5; 20), C(7; -16) thẳng hàng.

A
$x = - \frac{1}{3}$
B
$x = \frac{1}{3}$
C
$x = - 3$
D
$x = 3$

Đáp án : C

Lời giải :

Đường thẳng BC có dạng: $y = a x + b$

Vì điểm B(-5; 20) thuộc đường thẳng BC nên $20 = - 5 a + b,$ $b = 20 + 5 a (1)$

Vì điểm C(7; -16) thuộc đường thẳng BC nên $- 16 = 7 a + b (2)$

Thay (1) vào (2) ta có: $- 16 = 7 a + 20 + 5 a$

$12 a = - 36$

$a = - 3$ nên $b = 20 + 5. (- 3) = 5$

Do đó đường thẳng BC có dạng: $y = - 3 x + 5$

Để 3 điểm A, B, C thẳng hàng thì điểm A(x; 14) thuộc đường thẳng BC.

Do đó, $14 = - 3 x + 5$

$- 3 x = 9$

$x = - 3$

Câu 42 : Có bao nhiêu đường thẳng đi qua A(4; 3), cắt trục tung tại điểm có tung độ là một số nguyên dương, cắt trục hoành tại điểm có hoành độ làm một số nguyên tố.

A
Không có đường thẳng nào
B
1 đường thẳng
C
2 đường thẳng
D
3 đường thẳng

Đáp án : C

Lời giải :

Chứng minh dễ dàng được: Đường thẳng phải tìm cắt trục hoành tại điểm có hoành độ bằng a, cắt trục tung tại điểm có tung độ bằng b thì đường thẳng có dạng $\frac{x}{a} + \frac{y}{b} = 1$

Điểm A(4; 3) thuộc đường thẳng nên $\frac{4}{a} + \frac{3}{b} = 1.$

Do đó, $b = \frac{3 a}{a - 4} = 3 + \frac{12}{a - 4}$

Do a là số nguyên tố nên $a \geq 2, a - 4 \geq - 2$

Lần lượt cho $a - 4$ nhận các giá trị $\pm 2; \pm 1; 3; 4; 6; 12$ với chú ý rằng a là số nguyên tố và $b > 0$ , ta tìm được ${\begin{cases} a = 5 \\ b = 15 \end{cases}$ và ${\begin{cases} a = 7 \\ b = 7 \end{cases}$