Với tóm tắt lý thuyết Toán lớp 8 Bài 35: Định lí Pythagore và ứng dụng sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.
Lý thuyết Toán lớp 8 Bài 35: Định lí Pythagore và ứng dụng
A. Lý thuyết Định lí Pythagore và ứng dụng
1. Định lí Pythagore
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
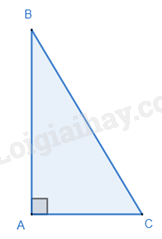
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do , suy ra .
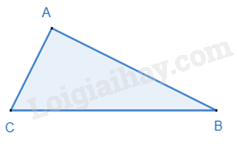
2. Định lí Pythagore đảo
Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
3. Ứng dụng của định lí Pythagore
a. Tính độ dài đoạn thẳng
Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c.
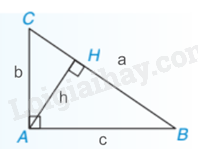
Ví dụ: Tam giác ABC vuông tại A có AB = 5cm, AC = 12cm thì BC =
b. Chứng minh tính chất hình học
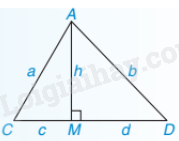
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD.
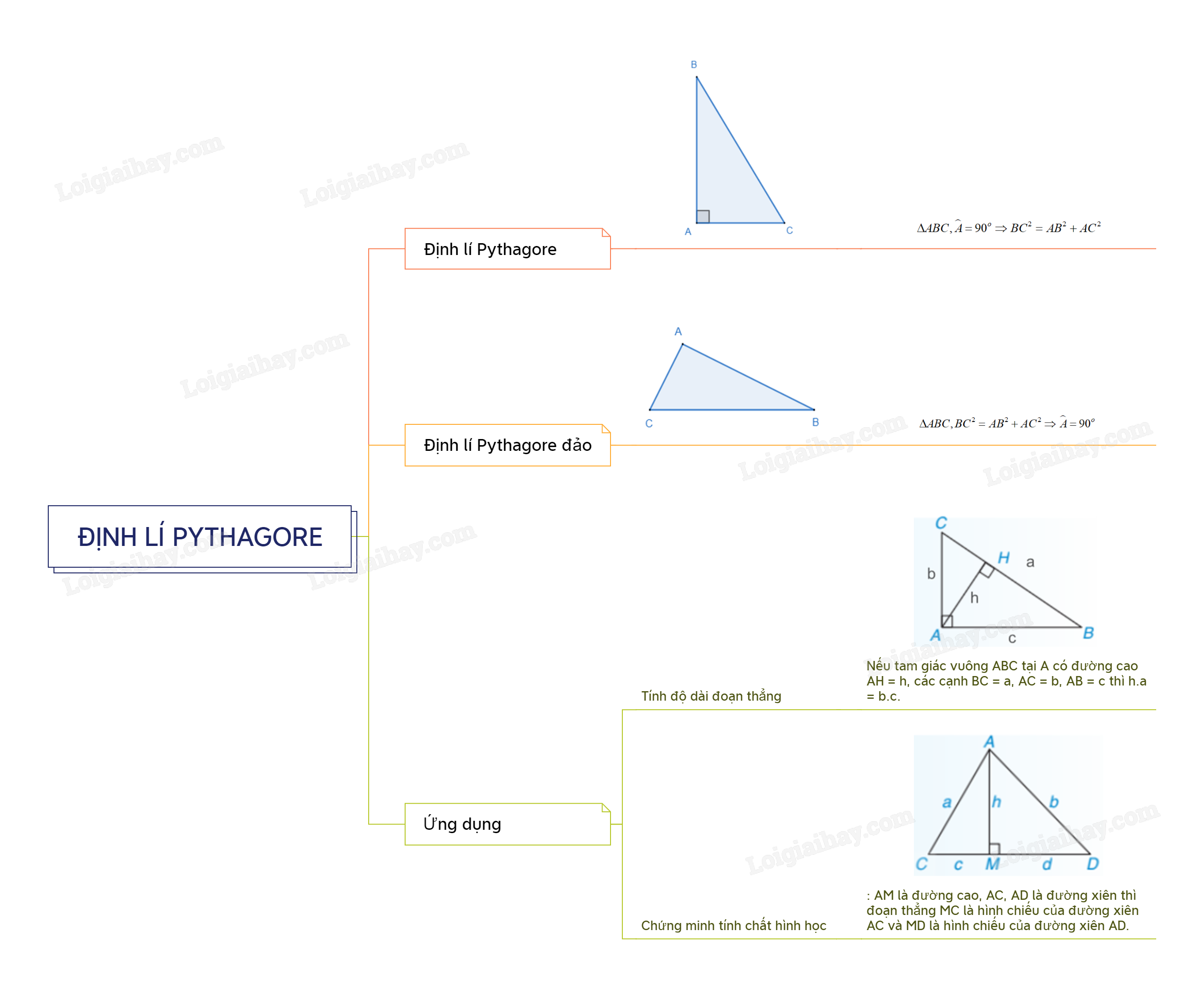
Sơ đồ tư duy Định lí Pythagore và ứng dụng
B. Bài tập Định lí Pythagore và ứng dụng
Đang cập nhật...
Xem thêm các bài tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 34: Ba trường hợp đồng dạng của hai tam giác
Lý thuyết Bài 35: Định lí Pythagore và ứng dụng
Lý thuyết Bài 36: Các trường hợp đồng dạng của hai tam giác vuông
Lý thuyết Bài 37: Hình đồng dạng
Lý thuyết Bài 38: Hình chóp tam giác đều
Lý thuyết Bài 39: Hình chóp tứ giác đều
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
