Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Định lí Pythagore và ứng dụng được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Định lí Pythagore và ứng dụng. Mời các bạn đón xem:
Bài tập Toán 8 Định lí Pythagore và ứng dụng
A. Bài tập Định lí Pythagore và ứng dụng
Bài 1: Cho hình thang cân ABCD (AB // CD). Giả sử . Tìm khẳng định đúng:
Hướng dẫn giải:
Đáp án : A
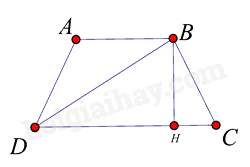
Kẻ tại H.
Xét tam giác vuông BDH, theo định lý Pytago ta có:
Xét tam giác vuông CBH, theo định lý Pytago ta có:
Suy ra:
DH + CH = CD; DH – CH = AB
Bài 2: Tứ giác ABCD có Chọn câu đúng.
Hướng dẫn giải:
Đáp án : B
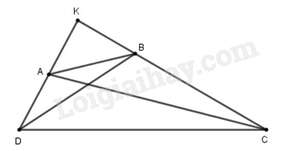
Gọi K là giao điểm AD, BC.
Vì nên
Xét ΔKAC vuông tại K ta có: AC2 = KC2 + KA2.
Xét ΔKBD vuông tại K ta có: BD2 = KB2 + KD2.
Xét ΔKBA vuông tại K ta có: BA2 = KA2 + KB2.
Xét ΔKBD vuông tại K ta có: CD2 = KC2 + KD2.
Từ đó BD2 + AC2 = KC2 + KA2 + KB2 + KD2
= (KB2 +KA2) + (KD2 + KC2) = AB2 + DC2.
Áp dụng định lí Pytago trong tam giác vuông
Bài 3: Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
Hướng dẫn giải:
Đáp án : D
Tam giác ABC vuông cân ở A nên theo định lý Pythagore ta có mà
AB = AC = 2 dm
Nên
Bài 4: Lựa chọn phương án đúng nhất:
Hướng dẫn giải:
Đáp án : B
Bài 5: Tìm câu sai trong các câu sau đây. Cho tam giác PQR vuông tại P. Khi đó:
Hướng dẫn giải:
Đáp án : D
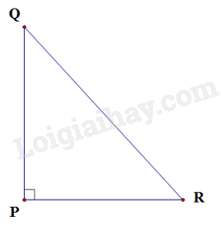
Tam giác PQR vuông tại P nên theo định lí Pythagore ta có: nên câu C đúng.
Vì độ dài đoạn thẳng là một số dương nên QR > PQ; QR > PR
Suy ra các câu A, B đúng.
Câu trả lời sai là câu D.
B. Lý thuyết Định lí Pythagore và ứng dụng
1. Định lí Pythagore
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
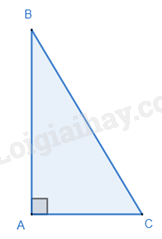
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do , suy ra .
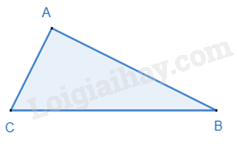
2. Định lí Pythagore đảo
Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
3. Ứng dụng của định lí Pythagore
a. Tính độ dài đoạn thẳng
Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c.
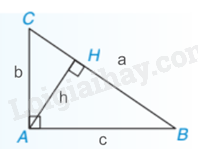
Ví dụ: Tam giác ABC vuông tại A có AB = 5cm, AC = 12cm thì BC =
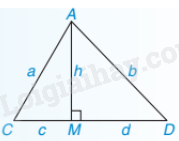
b. Chứng minh tính chất hình học
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD.
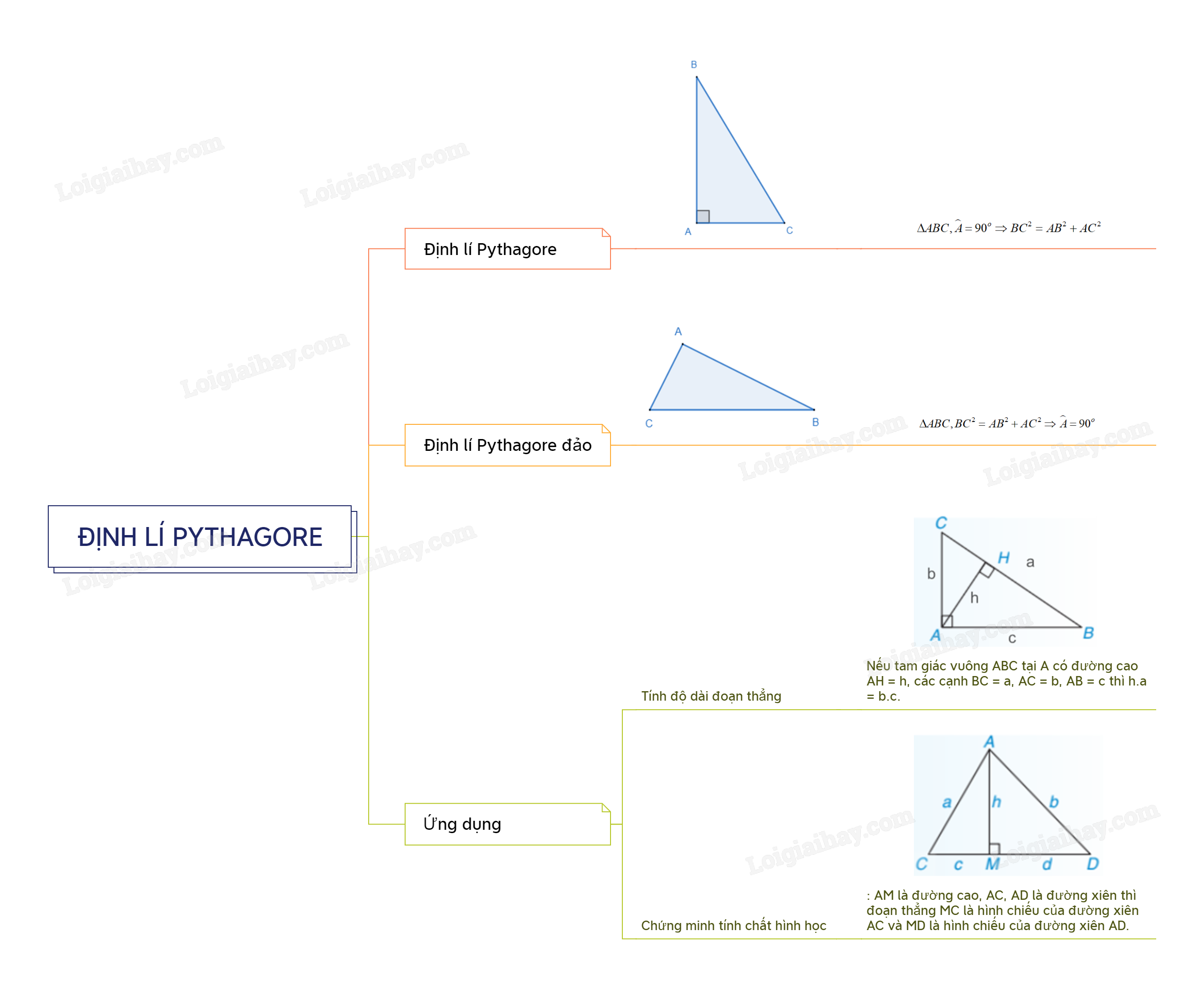
Sơ đồ tư duy Định lí Pythagore và ứng dụng