Với lời giải SBT Toán 8 trang 72 Tập 1 Bài tập cuối chương 3 trang 72 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 3 trang 72

Câu 1 trang 72 SBT Toán 8 Tập 1: Cho tam giác MNP vuông tại M. Biết MN = 40, MP = 9. Độ dài cạnh NP bằng

A. 41.

B. $\sqrt{1519}$.

C. 1681.

D. $\sqrt{41}$.

Lời giải:

Đáp án đúng là: A

Áp dụng định lý Pythagore trong tam giác MNP vuông tại M có:

NP² = MN² + MP² = 40² + 9² = 1681.

Suy ra $NP=\sqrt{1681}=41$.

Câu 2 trang 72 SBT Toán 8 Tập 1: Ba số nào sau đây không thể là độ dài ba cạnh của một tam giác vuông?

A. 3; 4; 5.

B. 5; 12; 13

C. 7; 24; 25.

D. 9; 40; 42.

Lời giải:

Đáp án đúng là: D

Ta có: 42² = 1764; 9² + 40² = 1681 nên 42² ≠ 9² + 40²

Do đó bộ ba số 9; 40; 42 không thể là độ dài ba cạnh của một tam giác vuông.

Câu 3 trang 72 SBT Toán 8 Tập 1: Một tứ giác có số đo ba góc lần lượt bằng 80°, 40°, 100°. Số đo góc còn lại bằng

A. 80°.

B. 120°.

C. 240°.

D. 140°.

Lời giải:

Đáp án đúng là: D

Gọi x là số đo góc còn lại của tứ giác

Tổng các góc của 1 tứ giác bằng 360° nên ta có:

x + 80° + 40° + 100° = 360°

Suy ra x = 360° ‒ 80° ‒ 40° ‒ 100° = 140°.

Câu 4 trang 72 SBT Toán 8 Tập 1: Cho hình thang cân có độ dài hai đáy lần lượt là 10 cm và 4 cm, độ dài cạnh bên là 5 cm. Hình thang đó có chiều cao là

A. 2 cm.

B. 3 cm.

C. 4 cm.

D. 6 cm.

Lời giải:

Đáp án đúng là: C

Giả sử ABCD hình thang cân (AB // CD) có AB = 4 cm, CD = 10 cm và AD = BC = 5 cm (hình vẽ).

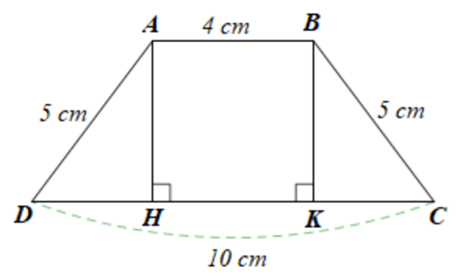
Kẻ hai đường cao AH và BK.

Xét ∆ADH vuông tại H và ∆BCK vuông tại K có:

AD = BC (hai cạnh bên bằng nhau của hình thang cân ABCD)

$\widehat{ADH}=\widehat{BCK}$ (do ABCD là hình thang cân)

Suy ra ∆ADH = ∆BCK (cạnh huyền – góc nhọn)

Do đó DH = CK (hai cạnh tương ứng)

Ta có: ABKH là hình chữ nhật nên AB = HK = 4 cm.

Mà DH + HK + CK = DC, suy ra $DH=CK=\frac{CD-HK}{2}=\frac{10-4}{2}=3$ (cm).

Áp dụng định lý Pythagore trong ∆ADH vuông tại H ta có:

AD² = AH² + DH², suy ra AH² = AD² ‒ DH² = 5² ‒ 3² = 16

Suy ra $AH=\sqrt{16}=4$ (cm).

Câu 5 trang 72 SBT Toán 8 Tập 1: Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo. Biết MN = 6, OM = 3, ON = 4. Độ dài của MP, NQ, PQ lần lượt là

A. 6; 8; 6.

B. 8; 6; 6.

C. 6; 6; 8.

D. 8; 8; 6.

Lời giải:

Đáp án đúng là: A

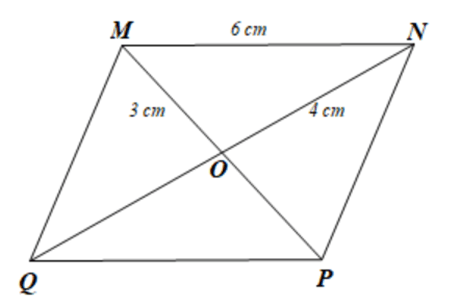
Do ABCD là hình bình hành nên MN = PQ = 6 cm.

Do O là giao điểm của hai đường chéo hình bình hành nên ON = OQ, OM = OP

Suy ra MP = 2OM = 2.3 = 6 cm và NQ = 2ON = 2.4 = 8 cm.