Với lời giải SBT Toán 11 trang 55 Tập 1 chi tiết trong Bài 10: Đường thẳng và mặt phẳng trong không gian sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian

Bài 4.1 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Gọi M là một điểm bất kì thuộc cạnh SC.

a) Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD).

b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD).

Lời giải:

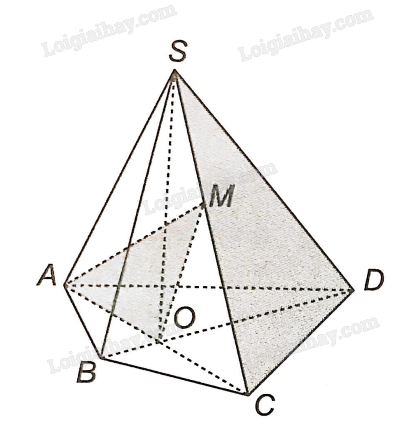
a) Ta thấy M thuộc AM, nằm trong mặt phẳng (AMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (AMO) và (SCD).

Ta thấy C thuộc đường thẳng AC (trùng với đường thẳng AO nên nó nằm trong mặt phẳng (AMO). C lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy C là điểm chung thứ hai của (AMO) và (SCD).

Vậy nên MC (hay SC) là giao tuyến của hai mặt phẳng (AMO) và (SCD).

b) Ta thấy M thuộc BM, nằm trong mặt phẳng (BMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (BMO) và (SCD).

Ta thấy D thuộc đường thẳng BD (trùng với đường thẳng BO nên nó nằm trong mặt phẳng (BMO). D lại thuộc SD, nằm trong mặt phẳng (SCD). Vậy D là điểm chung thứ hai của (BMO) và (SCD).

Vậy nên MD là giao tuyến của hai mặt phẳng (BMO) và (SCD).

Bài 4.2 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD.

a) Xác định giao tuyến của hai mặt phẳng (SAM) và (SCD).

b) Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD).

c) Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN).

Lời giải:

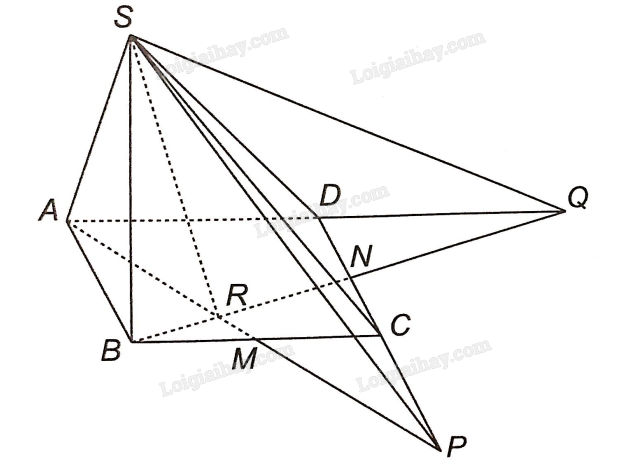
a) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SCD).

Trong mặt phẳng (ABCD): Gọi P là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SAM) và (SCD).

Vậy SP là giao tuyến của (SAM) và (SCD).

b) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SBN) và (SAD).

Trong mặt phẳng (ABCD): Gọi Q là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng  (SBN) và (SAD).

Vậy SQ là giao tuyến của  (SBN) và (SAD).

c) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SBN).

Trong mặt phẳng (ABCD): Gọi R là giao điểm của AM và BN => R là điểm chung thứ hai của mặt phẳng  (SAM) và (SBN).

Vậy SR là giao tuyến của  (SAM) và (SBN).

Bài 4.3 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Gọi P là điểm thuộc cạnh AD sao cho AP = 2 DP. Xác định giao tuyến của hai mặt phẳng (MNP) và (BCD).

Lời giải:

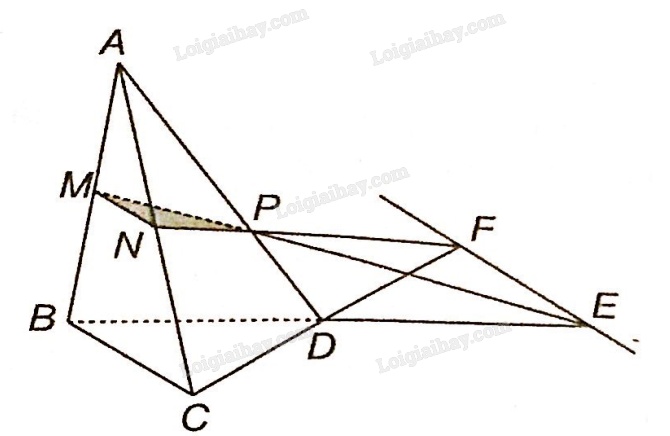
Trên mặt phẳng (ABD): gọi giao điểm của MP và BD là E. Vậy E là điểm chung thứ nhất của hai mặt phẳng (MNP) và (BCD)

Trên mặt phẳng (ACD): gọi giao điểm của NP và CD là F. Vậy F là điểm chung thứ hai của hai mặt phẳng (MNP) và (BCD).

Vậy giao tuyến của hai mặt phẳng (MNP) và (BCD) là đường thẳng EF.

Bài 4.4 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi P là một điểm thuộc cạnh BC sao cho PC = 2PB.

a) Xác định giao điểm của đường thẳng BD và mặt phẳng (MNP).

b) Xác định giao điểm của đường thẳng AC và mặt phẳng (MNP).

c) Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP).

Lời giải:

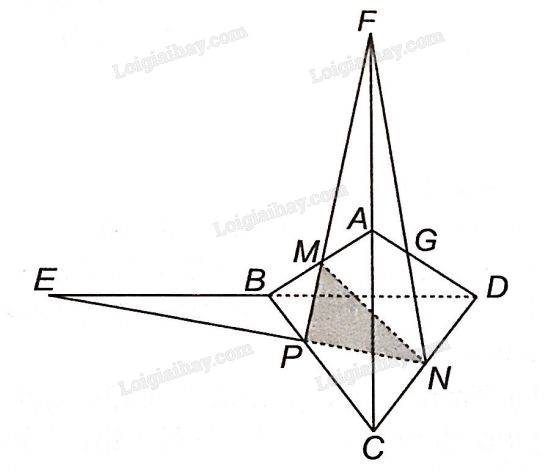
a) Trong mặt phẳng (BCD): Gọi E là giao điểm của BD và PN.

Vậy giao điểm của đường thẳng BD và mặt phẳng (MNP) là điểm E.

b) Trong mặt phẳng (ABC): gọi F là giao điểm của AC và MP.

Vậy giao điểm của đường thẳng AC và mặt phẳng (MNP) là điểm F.

c) Trong mặt phẳng (ADC): gọi G là giao điểm của AD và NF.

Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) là điểm G.

Bài 4.5 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi O là một điểm nằm trong tam giác SCD.

a) Xác định giao tuyến của hai mặt phẳng (SBO) và (SAC).

b) Xác định giao điểm của đường thẳng BO và mặt phẳng (SAC).

Lời giải:

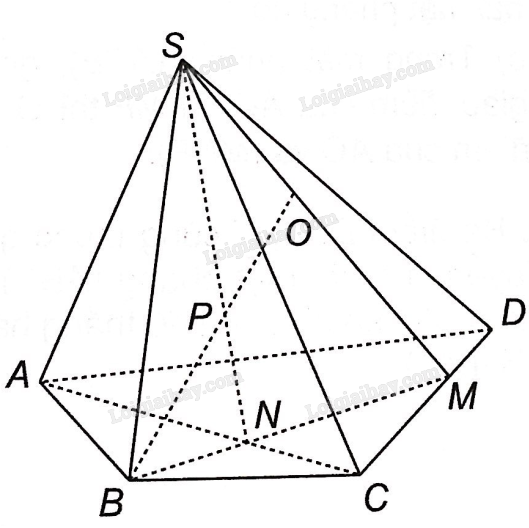
a) Ta thấy S là điểm chung đầu tiên của hai mặt phẳng (SBO) và (SAC).

Trong mặt phẳng (SCD): gọi M là điểm SO giao CD.

Trong mặt phẳng (ABCD): gọi N là giao điểm của BM và AC. Vậy N là điểm chung thứ hai của mặt phẳng (SAC) và (SBM) (trùng với mặt phẳng (SBO)).

Vậy giao tuyến của hai mặt phẳng (SBO) và (SAC) là SN.

b) Trong mặt phẳng (SAC): gọi P là giao điểm của đường thẳng SN và BO.

Vậy giao điểm của đường thẳng BO và mặt phẳng (SAC) là P.

Bài 4.6 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc cạnh AB, AC sao cho $\mathrm{A}\mathrm{E}=\frac{1}{2}\mathrm{B}\mathrm{E}$ và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.

a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).

b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).

Lời giải:

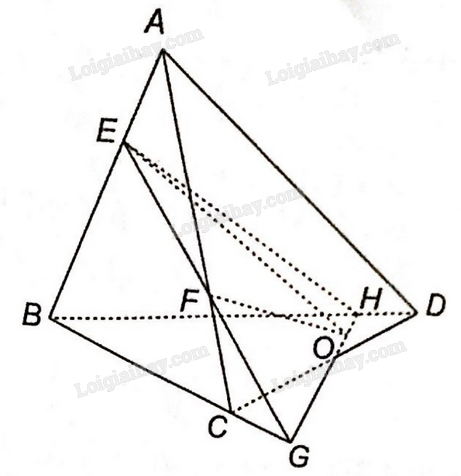
a) Ta thấy E thuộc AB, nằm trong mặt phẳng (ABD). Vậy E là điểm chung thứ nhất của hai mặt phẳng (ABD) và (OEF).

Trong mặt phẳng (ABC) gọi G là giao điểm của EF và BC.

Trong mặt phẳng (BCD), gọi H là giao điểm của BD và OG. Vậy H là một điểm chung của hai mặt phẳng (OEF) và (ABD)

Vậy EH là giao tuyến của hai mặt phẳng (OEF) và (ABD).

b) Trong mặt phẳng (ABD): Gọi I là giao điểm của EH và AD. Vậy I là giao điểm của AD và mặt phẳng (OEF).