Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 27: Khái niệm hàm số và đồ thị của hàm số chi tiết sách Toán 8 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 27: Khái niệm hàm số và đồ thị của hàm số

Giải Toán 8 trang 40 Tập 2

Mở đầu trang 40 Toán 8 Tập 2: Hình 7.1 là biểu đồ đoạn thẳng mô tả sản lượng tiêu thụ ô tô của thị trường Việt Nam trong 5 tháng đầu năm 2020. Em hãy cho biết trong tháng nào thì số lượng ô tô tiêu thụ là ít nhất.

Lời giải:

Quan sát biểu đồ ta thấy tháng 4 là tháng số lượng ô tô tiêu thụ ít nhất.

1. Khái niệm hàm số

HĐ1 trang 40 Toán 8 Tập 2: Quãng đường đi được S (km) của một ô tô chuyển động với vận tốc 60 km/h được cho bởi công thức S = 60t, trong đó t (giờ) là thời gian ô tô di chuyển.

a) Tính và lập bảng các giá trị tương ứng của S khi t nhận giá trị lần lượt là: 1; 2; 3; 4 (giờ).

b) Với mỗi giá trị của t, ta xác định được bao nhiêu giá trị tương ứng của S?

Lời giải:

a) Với t = 1 thì S = 60 . 1 = 60 (km);

Với t = 2 thì S = 60 . 2 = 120 (km);

Với t = 3 thì S = 60 . 3 = 180 (km);

Với t = 4 thì S = 60 . 4 = 240 (km).

Ta có bảng:

b) Với mỗi giá trị của t, ta xác định được một giá trị tương ứng của S.

HĐ2 trang 40 Toán 8 Tập 2: Nhiệt độ T (°C) tại các thời điểm t (giờ) của Hà Nội vào một ngày được cho trong các bảng sau:

a) Hãy cho biết nhiệt độ của Hà Nội và thời điểm 12 giờ trưa ngày hôm đó.

b) Với mỗi giá trị của t, ta xác định được bao nhiêu giá trị tương ứng của T?

Lời giải:

a) Nhiệt độ của Hà Nội vào 12 giờ trưa là 30 °C.

b) Với mỗi giá trị của t, ta xác định được một giá trị tương ứng của T.

Giải Toán 8 trang 41 Tập 2

Luyện tập 1 trang 41 Toán 8 Tập 2: Viết công thức tính thời gian di chuyển t (giờ) của một ô tô chuyển động trên quãng đường dài 150 km với vận tốc không đổi v (km/h). Thời gian di chuyển t có phải là một hàm số của vận tốc v không? Tính giá trị của t khi v = 60 km/h.

Lời giải:

+ Công thức tính thời gian di chuyển là $t=\frac{150}{v}$(giờ).

+ Thời gian di chuyển t là một hàm số của vận tốc v.

+ Có v = 60 (km/h) suy ra t = $\frac{150}{60}$ = 2,5 (giờ).

Vận dụng trang 41 Toán 8 Tập 2: Trử lại tình huống mở đầu, em hãy cho biết:

a) Tháng nào thì số lượng ô tô tiêu thụ là ít nhất và số lượng ô tô tiêu thụ trong tháng đó là bao nhiêu?

b) Nếu gọi y là số lượng ô tô tiêu thụ trong tháng x (x ∈ {1; 2; 3; 4; 5}) thì y có phải là một hàm số của x không? Tính giá trị của y khi x = 5.

Lời giải:

a) Tháng 4 số lượng ô tô tiêu thụ thấp nhất. Số lượng tiêu thụ trong tháng đó là 11 761 chiếc.

b) Với mỗi giá trị của x, ta xác định được một giá trị tương ứng của y nên y là một hàm số của x. 

Với x = 5, tức là số lượng ô tô tiêu thụ trong tháng 5 tương ứng là y = 19 081 chiếc.

Vậy y = 19 081 khi x = 5.

2. Mặt phẳng tọa độ

Giải Toán 8 trang 42 Tập 2

Câu hỏi trang 42 Toán 8 Tập 2: Hãy cho biết tọa độ của gốc tọa độ O

Lời giải:

Tọa độ của gốc O là O(0; 0).

Giải Toán 8 trang 43 Tập 2

Luyện tập 2 trang 43 Toán 8 Tập 2: a) Xác định tọa độ các điểm M, N, P, Q trong Hình 7.5.

b) Xác định các điểm R(2; –2) và S(–1; 2) trong Hình 7.5.

Lời giải:

a) Tọa độ các điểm M, N, P, Q là: M(–2; 4), N(1; –2), P(2; 0), Q(0; –3).

b) Các điểm R(2; –2) và S(–1; 2) được biểu diễn trên hình như sau:

Tranh luận trang 43 Toán 8 Tập 2: Pi: Những điểm có cả hoành độ và tung độ đều âm nằm ở góc phần tư thứ mấy?

Vuông: Em nghĩ là nằm ở góc phần tư thứ II.

Tròn: Không đúng, em nghĩ là nằm ở góc phần tư thứ III.

Ý kiến của em như thế nào?

Lời giải:

Những điểm có cả hoành độ và tung độ đều âm nằm ở góc phần tư thứ III.

Vậy ý kiến của Tròn đúng.

3. Đồ thị của hàm số

Giải Toán 8 trang 44 Tập 2

HĐ3 trang 44 Toán 8 Tập 2: Hàm số y = f(x) được cho bởi bảng sau:

a) Viết tập hợp {(x; y)} các cặp giá trị tương ứng của x và y.

b) Vẽ hệ trục tọa độ Oxy và biểu diễn các điểm có tọa độ là các cặp số trên. Tập hợp các điểm này gọi là đồ thị của hàm số y = f(x) đã cho.

Lời giải:

a) Tập hợp các cặp giá trị tương ứng của x và y là:

{(–2; –1); (–1; 0); (0; 1); (1; 2); (2; 3)}.

b) Ta biểu diễn các điểm đã cho như sau:

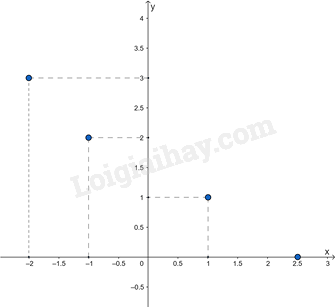
Luyện tập 3 trang 44 Toán 8 Tập 2: Vẽ đồ thị của hàm số y = f(x) cho bởi bảng sau:

Lời giải:

Ta có tập hợp các điểm của đồ thị hàm số y = f(x) là

{(– 3; 4); (– 1; 3,5); (1; 1); (2,5; 0)}.

Biểu diễn các điểm trên lên mặt phẳng tọa độ Oxy ta được đồ thị của hàm số y = f(x).

Bài tập

Bài 7.18 trang 44 Toán 8 Tập 2: Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng sau. Đại lượng y có phải là một hàm số của x không?

a)

b)

Lời giải:

a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (thuộc tập hợp {–3; –1; 0; 2; 4}) ta luôn xác định được chỉ một giá trị tương ứng của y (y luôn bằng 1).

b) Đại lượng y không là hàm số của x vì với x = 1 ta xác định được hai giá trị tương ứng của y là y = 1 và y = 2.

Giải Toán 8 trang 45 Tập 2

Bài 7.19 trang 45 Toán 8 Tập 2: Cho hàm số y = f(x) = $\frac{4}{x}$.

a) Tính f(–4); f(8).

b) Hoàn thành bảng sau vào vở:

Lời giải:

a) Ta có f(–4) = $\frac{4}{-4}=-1$; f(8) = $\frac{4}{8}=\frac{1}{2}$

b) Ta có f(– 2) = $\frac{4}{-2}=-2$; f(2) = $\frac{4}{2}=2$; f(3) = $\frac{4}{3}$.

Với y = f(x) = – 4 thì $\frac{4}{x}=-4$, suy ra x = – 1. 

Với y = f(x) = 8 thì $\frac{4}{x}=8$, suy ra x = $\frac{1}{2}$  

Vậy ta điền được bảng như sau:

Bài 7.20 trang 45 Toán 8 Tập 2: a) Xác định tọa độ của các điểm A, B, C, D trong Hình 7.8.

b) Xác định các điểm E(0; –2) và F(2; –1) trong Hình 7.8.

Lời giải:

a) Có A(–3; 4), B(–2; –2), C(1; –3), D(3; 0).

b) Ta có các điểm E(0; –2) và F(2; –1) được biểu diễn như sau:

Bài 7.21 trang 45 Toán 8 Tập 2: Hàm số y = f(x) được cho bởi bảng sau:

Vẽ đồ thị của hàm số y = f(x).

Lời giải:

Tập hợp các điểm của đồ thị hàm số y = f(x) là

{(– 2; – 5); (– 1; – 2,5); (0; 0); (1; 2,5); (2; 5)}.

Biểu diễn các điểm trên trên cùng một mặt phẳng tọa độ ta được đồ thị hàm số y = f(x) như sau:

Bài 7.22 trang 45 Toán 8 Tập 2: Cân nặng và tuổi của bốn bạn An, Bình, Hưng, Việt được biểu diễn trên mặt phẳng tọa độ như Hình 7.9.

(Do số liệu về tuổi và cân nặng rất chênh lệch nên trong Hình 7.9, ta đã lấy một đơn vị dài trên trục hoành bằng 5 lần một đơn vị dài trên trục tung).

Hãy cho biết:

a) Ai là người nặng nhất và nặng bao nhiêu?

b) Ai là người ít tuổi nhất và bao nhiêu tuổi?

c) Bình và Việt ai nặng hơn và ai nhiều tuổi hơn?

d) Thay dấu ‘?’ bằng số thích hợp để hoàn thành bảng sau vào vở:

Theo bảng đã hoàn thành, cân nặng có phải là hàm số của tuổi không? Vì sao?

Lời giải:

a) Hưng là người nặng nhất, nặng 50 cân.

b) An là người ít tuổi nhất, 11 tuổi.

c) Bình nặng hơn Việt và Bình kém tuổi Việt hay Việt nhiều tuổi hơn Bình.

d) Dựa vào Hình 7.9, ta có bảng sau:

Theo bảng đã hoàn thành, ta thấy cân nặng không phải là hàm số của tuổi vì cùng tuổi là 14 nhưng Hưng và Việt có cân nặng khác nhau.

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 37)

Bài 27: Khái niệm hàm số và đồ thị của hàm số

Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Bài 29: Hệ số góc của đường thẳng

Luyện tập chung (trang 55)

Lý thuyết Khái niệm hàm số và đồ thị của hàm số

1. Hàm số

Khái niệm:

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.

Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.

Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 34⁰C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.

Chú ý: Khi y là hàm số của x, ta viết $y=f(x);y=g(x),...$

Ví dụ: Cho hàm số y = f(x) = x + 3.

f(-2) = -2 + 3 = 1;            f(0) = 0 + 3 = 3

2. Mặt phẳng tọa độ

Khái niệm: Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ.

• Ox nằm ngang gọi là trục hoành;
• Oy thẳng đứng gọi là trục tung;
• O gọi là gốc tọa độ.

Tọa độ của một điểm:

Trong mặt phẳng tọa độ, mỗi điểm M xác định duy nhất một cặp số $(x_0;y_0)$ và mỗi cặp số $(x_0;y_0)$ xác định duy nhất một điểm M.

Cặp số $(x_0;y_0)$ gọi là tọa độ của M, kí hiệu là M(x₀,y₀), trong đó x₀ là hoành độ, y₀ là tung độ của điểm M.

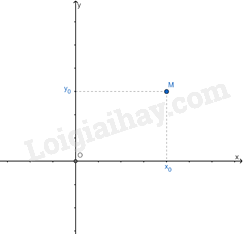
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.

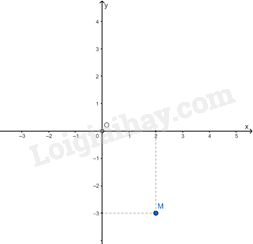
3. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng tọa độ.

Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng: