Tailieumoi.vn xin giới thiệu tài liệu Trắc nghiệm Toán lớp 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên sách Cánh diều. Tài liệu gồm 25 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:
Trắc nghiệm Toán lớp 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên
Phần 1. Trắc nghiệm Phép tính lũy thừa với số mũ tự nhiên
Câu 1: Viết tích 10 . 10 . 10 . 100 dưới dạng lũy thừa cơ số 10, ta được:
A. 104
B. 105
C. 106
D. 107
Lời giải
Ta có: 10 . 10 . 10 . 100 = 10 . 10 . 10 . 10 . 10 = 105
Chọn đáp án B.
Câu 2: Với a ≠ 0 và , ta có: am : an = ?
A. am : n
B. a
C. am – n
D. am + n
Lời giải
Theo công thức chia hai lũy thừa cùng cơ số, ta có:
am : an = am – n (với a ≠ 0 và m ≥ n )
Chọn đáp án C.
Câu 3: Tính giá trị của lũy thừa 54 ta được:
A. 20
B. 25
C. 125
D. 625
Lời giải
Ta có: 54 = 5 . 5 . 5 . 5 = 25 . 5 . 5 = 125 . 5 = 625
Chọn đáp án D.
Câu 4: Viết 73 . 77 dưới dạng một lũy thừa ta được:
A. 721
B. 710
C. 74
D. 71
Lời giải
Áp dụng công thức nhân hai lũy thừa cùng cơ số, ta có: 73 . 77 = 73 + 7 = 710.
Chọn đáp án B.
Câu 5: Viết 189 : 183 dưới dạng một lũy thừa ta được:
A. 1812
B. 183
C. 186
D. 1810
Lời giải
Áp dụng công thức chia hai lũy thừa cùng cơ số, ta có: 189 : 183 = 189 – 3 = 186.
Chọn đáp án C.
Câu 6: Viết tích sau dưới dạng lũy thừa: 6 . 6 . 6 . 6 . 6
A. 66
B. 65
C. 56
D. 64
Lời giải
Ta có: 6.6.6.6.6 = 65 (tích của 5 thừa số 6).
Chọn đáp án B.
Câu 7: Chọn câu đúng.
A. am . an = am + n
B. a . a . a . a . a = 5a
C. am . an = am.n
D. a1 = 1
Lời giải
Ta có với a, m, n ∈ N thì:
+) am . an = am + n (nhân hai lũy thừa cùng cơ số) nên A đúng và C sai.
+) a . a . a . a . a = a5 (tích của 5 thừa số a) nên B sai.
+) a1 = a nên D sai.
Chọn đáp án A.
Câu 8: Chọn câu sai. Cho lũy thừa: 25 thì
A. 2 là cơ số
B. 5 là số mũ
C. 2 là số mũ
D. 25 = 32
Lời giải
Ta có: với lũy thừa 25 thì 2 được gọi là cơ số, 5 được gọi là số mũ nên đáp án A, B đúng và đáp án C sai.
Lại có: 25 = 2 . 2 . 2 . 2 . 2 = 4 . 2 . 2 . 2 = 8 . 2 . 2 = 16 . 2 = 32 nên đáp án D đúng.
Chọn đáp án C.
Câu 9: Chọn câu sai. 38 được đọc là:
A. ba mũ tám
B. ba lũy thừa tám
C. lũy thừa bậc tám của ba
D. tám mũ ba
Lời giải
Ta có: 38 đọc là “ba mũ tám” hoặc “ba lũy thừa tám” hoặc “lũy thừa bậc tám của ba” nên đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Câu 10: Viết số 81 dưới dạng lũy thừa. Chọn câu sai.
A. 34
B. 92
C. 811
D. 29
Lời giải
Ta có: 81 = 811
81 = 9 . 9 = 92
81 = 3 . 3 . 3 . 3 = 34
Vậy viết 81 dưới dạng lũy thừa, ta được: 81 = 811 = 92 = 34.
Do đó đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Câu 11: Chọn đáp án sai.
A. 53 < 35
B. 34 > 25
C. 43 = 26
D. 43 > 82
Lời giải
Ta có:
+) 53 = 125; 35 = 243 suy ra 53 < 35 nên A đúng.
+) 34 = 81; 25 = 32 suy ra 34 > 25 nên B đúng.
+) 43 = 64; 26 = 64 suy ra 43 = 26 nên C đúng.
+) 43 = 64; 82 = 64 suy ra 43 = 82 nên D sai.
Chọn đáp án D.
Câu 12: Tìm số tự nhiên n thỏa mãn 3n = 81.
A. n = 2
B. n = 3
C. n = 4
D. n = 8
Lời giải
Ta có: 34 = 81 nên 3n = 34, do đó n = 4.
Chọn đáp án C.
Câu 13: Viết cấu tạo số 2 017 dưới dạng tổng các lũy thừa của 10 là:
A. 2 017 = 2 . 104 + 102 + 7 . 100
B. 2 017 = 2 . 103 + 10 + 7 . 100
C. 2 017 = 2 . 104 + 102 + 7 . 10
D. 2 017 = 2 . 103 + 102 + 7 . 100
Lời giải
Ta có: 2 017 = 2 . 1 000 + 0 . 100 + 1 . 10 + 7 . 1 = 2 . 103 + 10 + 7 . 100.
Chọn đáp án B.
Câu 14: Viết kết quả phép tính 63 . 2 . 64 . 3 dưới dạng một lũy thừa ta được:
A. 66
B. 67
C. 68
D. 69
Lời giải
Ta có: 63 . 2 . 64 . 3 = (63 . 64) . (2 . 3) = 63 + 4 . 6 = 67 . 61 = 67 + 1 = 68.
Chọn đáp án C.
Câu 15: Chọn kết luận đúng trong các kết luận sau:
A. 33 . 34 = 312
B. 30 = 0
C. 42 : 23 = 2
D. 55 : 5 = 14
Lời giải
Ta có:
33 . 34 = 33 + 4 = 37 nên đáp án A sai
30 = 1 (quy ước) nên đáp án B sai
42 : 23 = 4 . 4 : 23 = 2 . 2 . 2 . 2 : 23 = 24. 23 = 24 – 3 = 21 = 2 nên C đúng
55 : 5 = 55 – 1 = 54 ≠ 14 nên D sai
Chọn đáp án C.
Câu 16: Chọn đáp án đúng?
A. 52 . 53 . 54 = 510
B. 52 . 53 . 25 = 57
C. 53 . 5 = 253
D. 51 = 1
Lời giải
Ta có:
+) 52 . 53 . 54 = 52 + 3 + 4 = 59 nên đáp án A sai.
+) 52 . 53 . 25 = 52 . 53 . 5 . 5 = 52 . 53 . 52 = 52 + 3 + 2 = 57 nên đáp án B đúng.
+) 53 . 5 = 53 + 1 = 54 nên đáp án C sai.
+) 51 = 5 nên đáp án D sai.
Chọn đáp án B.
Câu 17: Tính 24 + 16 ta được kết quả dưới dạng lũy thừa là?
A. 220
B. 24
C. 25
D. 210
Lời giải
Ta có: 24 + 16 = 24 + 2 . 2 . 2 . 2 = 24 + 24 = 2 . 24 = 21 + 4 = 25
Chọn đáp án C.
Câu 18: Số tự nhiên được biểu diễn bởi 2 . 103 + 7 . 102 + 8 . 10 + 7 . 100 là:
A. 2 787
B. 2 7870
C. 278
D. 2 780
Lời giải
Ta có:
2 . 103 + 7 . 102 + 8 . 10 + 7 . 100
= 2 . 1 000 + 7 . 100 + 8 . 10 + 7 . 1
= 2 000 + 700 + 80 + 7 = 2 787
Chọn đáp án A
Câu 19: Số tự nhiên n thỏa mãn 2n = 42 là:
A. n = 3
B. n = 4
C. n = 5
D. n = 6
Lời giải
Ta có:
42 = 4 . 4 = 2 . 2 . 2 . 2 = 24
Vì 2n = 42 nên 2n = 24
Vậy n = 4.
Chọn đáp án B
Câu 20: Viết kết quả phép tính 122 . 2 . 125 . 6 dưới dạng một lũy thừa, ta được:
A. 129
B. 128
C. 127
D. 126
Lời giải
Ta có: 122 . 2 . 125 . 6 = 122 . 125 . (2 . 6) = 122 + 5 . 12 = 127 . 121 = 127 + 1 = 128.
Chọn đáp án B.
Câu 21: Tìm số tự nhiên n thỏa mãn 25n : 253 = 255?
A. n = 3
B. n = 6
C. n = 7
D. n = 8
Lời giải
Ta có: 25n : 253 = 255
Vì 25n : 253 = 25n – 3
Nên ta được: 25n – 3 = 255
Do đó: n – 3 = 5
Suy ra: n = 5 + 3 = 8
Vậy n = 8.
Chọn đáp án D.
Câu 22: Tìm số tự nhiên n thỏa mãn 4n = 43 . 45?
A. n = 32
B. n = 16
C. n = 8
D. n = 4
Lời giải
Ta có: 43 . 45 = 43 + 5 = 48 nên 4n = 48 suy ra n = 8.
Chọn đáp án C.
Câu 23: Tìm số tự nhiên m thỏa mãn 202018 < 20m < 202020 ?
A. m = 2 020
B. m = 2 019
C. m = 2 018
D. m = 20
Lời giải
Ta có: 202018 < 20m < 202020
Suy ra: 2 018 < m < 2 020
Mà m là số tự nhiên nên m = 2 019.
Vậy m = 2 019.
Chọn đáp án B.
Câu 24: Không tính các lũy thừa, hãy so sánh A và B với A = 2711 và B = 818.
A. A = B
B. A > B
C. A < B
D. A ≤ B
Lời giải
Ta có: A = 2711 = (3 . 3 . 3)11 = (33)11 = 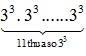 =
= 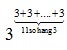 = 33 . 11 = 333
= 33 . 11 = 333
Lại có: B = 818 = (3 . 3 . 3 . 3)8 = (34)8 = 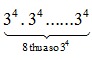 =
= 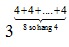 = 34 . 8 = 332
= 34 . 8 = 332
Vì 33 > 32 nên 333 > 332 hay 2711 > 818
Vậy A > B.
Chọn đáp án B.
Câu 25: Chữ số tận cùng của số 475 là:
A. 7
B. 5
C. 4
D. 1
Lời giải
Ta có: 47 . 47 = 47 . (40 + 7) = 47 . 40 + 47 . 7
= 47 . 40 + (40 + 7) . 7
= 47 . 40 + 40 . 7 + 7 . 7
Suy ra 47 . 47 có chữ số tận cùng như chữ số tận cùng của 7 . 7 = 49.
Do đó 472 có chữ số tận cùng là 9
Tương tự (472)2 có chữ số tận cùng của 92 = 81.
Mà (472)2 = 472 . 472 = 47 . 47 . 47 . 47 = 474
Do đó 474 có chữ số tận cùng là 1.
Vậy 475 = 474 . 47 có chữ số tận cùng là 1 . 7 = 7.
Chọn đáp án A.
Phần 2. Lý thuyết Phép tính lũy thừa với số mũ tự nhiên
I. Phép nâng lên lũy thừa
Lũy thừa bậc n của a, kí hiệu , là tích của n thừa số a:
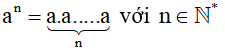
Trong đó:
a được gọi là cơ số
n được gọi là số mũ.
Quy ước: a1=a
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Chú ý:
+ an đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bậc n của a”.
+ a2 còn được gọi là “a bình phương” hay “bình phương của a”.
+ a3 còn được gọi là “a lập phương” hay “lập phương của a”.
Ví dụ:
7 . 7 . 7 . 7 = 74 (đọc là 7 mũ 4 hoặc là 7 lũy thừa 4, hoặc lũy thừa bậc bốn của 7)
16 = 2 . 2 . 2 . 2 = 24
Lưu ý: Với n là số tự nhiên khác 0, ta có: 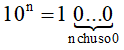
Ví dụ: 105 = 10 . 10 . 10 . 10 . 10 = 100 000
II. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
am . an = am + n
Ví dụ:
+) 23 . 24 = 23 + 4 = 27
+) a2 . a1 = a2 + 1 = a3
+) 42 . 45 = 42 + 5 = 47
III. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
am : an = am - n (a # 0, m ≥ n)
Quy ước: a0 = 1 (a # 0) .
Ví dụ:
+ 97 : 93 = 97 - 3 = 94
+ 76 : 7 = 76 : 71 = 76 - 1 = 75
+ 33 : 33 = 33 - 3 = 30 = 1
Xem thêm các bài trắc nghiệm Toán lớp 6 Cánh Diều hay, chi tiết khác:
Trắc nghiệm Bài 4: Phép nhân và phép chia các số tự nhiên
Trắc nghiệm Bài 5: Phép tính lũy thừa với số mũ tự nhiên
Trắc nghiệm Bài 6: Thứ tự thực hiện các phép tính
Trắc nghiệm Bài 7: Quan hệ chia hết. Tính chất chia hết
Trắc nghiệm Bài 8: Dấu hiệu chia hết cho 2, cho 5