Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 6 Chương 8: Những hình học cơ bản sách Kết nối tri thức. Tài liệu gồm 12 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:
Trắc nghiệm Toán lớp 6 Chương 8: Những hình học cơ bản
Phần 1. Trắc nghiệm Chương 8: Những hình học cơ bản
Câu 1. Cho đoạn thẳng AB = 14cm, điểm I nằm giữa hai điểm A và B;
AI =4 cm. Điểm O nằm giữa hai điểm I, B sao cho AI = OB. Gọi M, N lần lượt là trung điểm của đoạn thẳng AI, OB. Tính độ dài đoạn thẳng MN.
A. 10cm
B. 8cm
C. 12cm
D. 6cm
Đáp án: A
Giải thích:
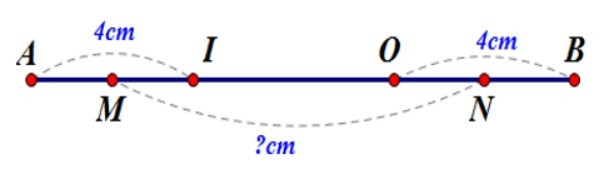
Vì điểm I nằm giữa hai điểm A và B nên:
⇒ AI + IB = AB ⇒ 4cm; IB = 14cm ⇒ IB = 14cm − 4cm = 10cm
Vì AI = OB = 4cm ; N là trung điểm của đoạn thẳng OB nên:
ON = NB = OB : 2 = 4cm : 2 = 2cm
Vì điểm M là trung điểm của đoạn thẳng AI nên:
Ta có điểm M, N nằm giữa hai điểm A, B nên:
⇒ AM + MN + NB = AB ⇒ 2cm + MN + 2cm = 14cm
⇒ MN = 14cm − 2cm − 2cm
⇒ MN = 10cm
Đáp án cần chọn là: A
Câu 2. Cho 24 điểm trong đó có 6 điểm thẳng hàng. Qua 2 điểm ta kẻ được một đường thẳng. Hỏi kẻ được tất cả bao nhiêu đường thẳng?
A. 276
B. 290
C. 262
D. 226
Đáp án: C
Giải thích:
Giả sử trong 24 điểm không có 3 điểm nào thẳng hàng tất cả vẽ được:
(đường thẳng)
Qua 6 điểm thẳng hàng vẽ được số đường thẳng là: (đường thẳng)
Nhưng qua 6 điểm thẳng hàng chỉ vẽ được một đường thẳng
Nên qua 24 điểm trong đó có 6 điểm thẳng hàng vẽ được:
276 – 15 + 1 = 262 (đường thẳng)
Đáp án cần chọn là: C
Câu 3. Cho M thuộc đoạn thẳng AB, AM = 4cm, AB = 6cm. Gọi O là trung điểm của đoạn AB.
Tính MO.
A. MO = 4cm
B. MO = 3cm
C. MO = 1cm
D. MO = 2cm
Đáp án: C
Giải thích:

) Vì nên M nằm giữa A và B
⇒AM + MB = AB ⇒ BM = AB – MB = 6 – 4 = 2cm.
+) Vì O là trung điểm của AB nên:
Vì và ) AO < AM (3cm < 4cm) nên O nằm giữa A và M suy ra:
AO + OM = AM
⇒ OM = AM – AO = 4 – 3 = 1cm
Đáp án cần chọn là: C
Câu 4. Cho M thuộc đoạn thẳng AB, AM = 4cm, AB = 6cm. Gọi O là trung điểm của đoạn AB.
Trên AB lấy điểm I sao cho AI = 3,5cm. Lấy điểm P là trung điểm của AO. Chọn câu đúng.
A. Điểm I là trung điểm của OM
B. Điểm O nằm giữa I và P
C. IP = 2cm
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:

+ ) Vì và AO < AI (3cm < 3,5cm) nên O nằm giữa A và I suy ra:
AO + OI = AI
⇒ OI = AI – AO = 3,5 – 3 = 0,5cm (1)
Vì và AI < AM (3,5cm < 4cm) nên I nằm giữa A và M suy ra:
AI + IM = AM ⇒ IM = AM – AI = 4 − 3,5 = 0,5cm(2)
Từ (1) và (2) suy ra OI = IM (3)
Vì O nằm giữa A và I nên A và O nằm cùng phía đối với I . Mà I nằm giữa A và M nên A và M nằm khác phía đối với I ⇒ O và M nằm khác phía đối với I suy ra I nằm giữa M và O (4)
Từ (3) và (4) suy ra I là trung điểm của OM.
+) Vì P là trung điểm của AO nên:
Vì
⇒ O nằm giữa A và M
Suy ra A và M nằm khác phía đối với O
Vì P là trung điểm của AO nên A, P cùng phía đối với O.
Vì I là trung điểm của OM nên I, M cùng phía đối với O.
Từ đó suy ra I nằm giữa O và P ⇒OP + IO = IP ⇒ IP = 1,5 + 0,5 = 2cm
Đáp án cần chọn là: D
Câu 5. Em hãy chọn phát biểu sai trong các phát biểu sau:
A. Góc bẹt là góc có hai cạnh là hai tia đối nhau
B. được gọi là góc tù nếu
C. Nếu tia Ot là tia phân giác của thì
D. Tam giác MNP là hình gồm các đoạn thẳng MN, MP và NP khi ba điểm M, N, P không thẳng hàng.
Đáp án: B
Giải thích:
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau (đúng loại A)
+ được gọi là góc tù nếu
(sai vìđược gọi là góc tù nếu chọn B)
+ Nếu tia Ot là tia phân giác của thì
(đúng loại C)
+ Tam giác MNP là hình gồm các đoạn thẳng MN, MP và NP khi ba điểm M, N, P không thẳng hàng. (đúng loại D)
Đáp án cần chọn là: B
Câu 6. Cho ba điểm không thẳng hàng O, A, B. Tia OxOx nằm giữa hai tia OA, OB khi và chỉ khi tia Ox cắt
A. Đoạn thẳng AB
B. Đường thẳng AB
C. Tia AB
D. Tia BA
Đáp án: A
Giải thích:
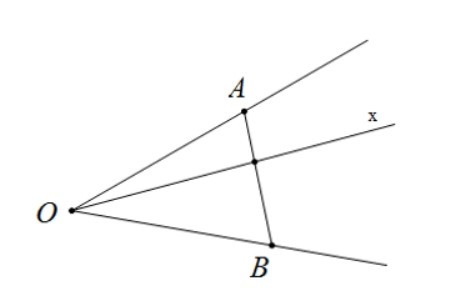
Tia Ox nằm giữa hai tia OA và OB khi tia Ox cắt đoạn thẳng AB
Đáp án cần chọn là: A
Câu 7. Cho 10 tia phân biệt chung gốc O. Xóa đi ba tia trong đó thì số góc đỉnh O giảm đi bao nhiêu?
A. 3
B. 12
C. 24
D. 48
Đáp án: C
Giải thích:
Với 10 tia chung gốc O thì số góc tạo thành là góc
Với 7 tia chung gốc O thì số góc tạo thành là góc
Vậy số góc giảm đi khi xóa đi ba tia là
45 – 21 = 24 góc
Đáp án cần chọn là: C
Câu 8. Cho 20 điểm phân biệt, trong đó có a điểm thẳng hàng. Cứ 2 điểm, ta vẽ một đường thẳng. Tìm a , biết vẽ được tất cả 170 đường thẳng.
A. a = 9
B. a = 6
C. a = 7
D. a = 8
Đáp án: C
Giải thích:
Trong 20 điểm mà không có ba điểm nào thẳng hàng thì ta vẽ được:
19.20:2 = 190 đường thẳng.
Trong a điểm mà không có ba điểm nào thẳng hàng thì ta vẽ được:
(a − 1).a : 2 đường thẳng.
Nhưng do có a điểm thẳng hàng nên chỉ có 1 đường thẳng được vẽ. Do đó,theo bài ra ta có:
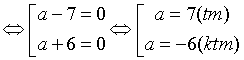
Vậy có 7 điểm thẳng hàng.
Đáp án cần chọn là: C
Câu 9. Cho 101 đường thẳng trong đó bất cứ hai đường thẳng nào cũng cắt nhau, không có ba đường thẳng nào đồng quy. Tính số giao điểm của chúng.
A. 10010 giao điểm
B. 5005 giao điểm
C. 10100 giao điểm
D. 5050 giao điểm
Đáp án: D
Giải thích:
Mỗi đường thẳng cắt 100 đường thẳng còn lại tạo nên 100 giao điểm .
Vì có 101 đường thẳng nên có 101.100 giao điểm .
Nhưng mỗi giao điểm đã được tính hai lần nên chỉ có
101.100:2=5050 ( giao điểm).
Đáp án cần chọn là: D
Câu 10. Có bao nhiêu đường thẳng đi qua hai điểm phân biệt A và B?
A. 1
B. 2
C. 3
D. Vô số
Đáp án: A
Giải thích:
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước. Vậy có duy nhất 1 đường thẳng đi qua hai điểm A và B.
Đáp án cần chọn là: A
Câu 11. Cho hình vẽ. Em hãy chọn đáp án đúng.

A. A nằm giữa hai điểm B và C
B. B nằm giữa hai điểm A và C
C. C nằm giữa hai điểm A và B
D. Không có điểm nào nằm giữa hai điểm còn lại
Đáp án: B
Giải thích:
Quan sát hình vẽ ta thấy điểm B nằm giữa hai điểm A và C.
Đáp án cần chọn là: B
Câu 12. Cho điểm M nằm giữa điểm N và P như hình vẽ. Kết luận nào sau đây là đúng ?

A. Tia NM trùng với tia MP
B. Tia MP trùng với tia NP
C. Tia PM trùng với tia PN
D. Tia MN trùng với tia MP.
Đáp án: C
Giải thích:
Nhận xét:
+ Đáp án A: Hai tia NM và MP là hai tia không chung gốc nên loại đáp án A.
+ Đáp án B: Hai tia MP và NP là hai tia không chung gốc nên loại đáp án B.
+ Đáp án C: thấy hai tia PN và PM là hai tia cùng chung gốc P và tạo thành nửa đường thẳng nên hai tia PN và PM là hai tia trùng nhau, do đó chọn đáp án C.
+ Đáp án D: Hai tia MN và MP là hai tia chung gốc nhưng tạo thành một đường thẳng nên hai tia MN và MP là hai tia đối nhau, do đó loại đáp án D.
Đáp án cần chọn là: C
Câu 13. Cho hình vẽ:

Hình vẽ trên có bao nhiêu tia chung gốc B:
A. 5
B. 3
C. 4
D. 2
Đáp án: A
Giải thích:

Hình vẽ trên có các tia chung gốc B là: BA, Bx, By, BC và BD. Vậy có tất cả 5 tia chung gốc B.
Đáp án cần chọn là: A
Câu 14. Cho hình vẽ sau. Chọn câu đúng.
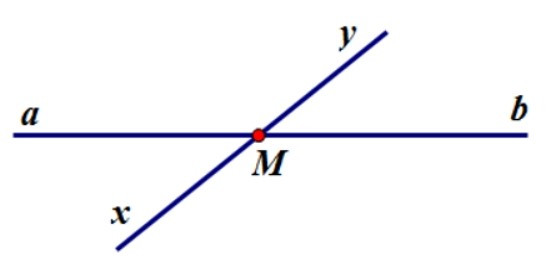
A. Điểm M thuộc đường thẳng xy nhưng không thuộc đường thẳng ab
B. Hai đường thẳng xy và ab không có điểm chung
C. Đường thẳng xy cắt đường thẳng ab tại M
D. Đường thẳng xy và ab có hai điểm chung
Đáp án: C
Giải thích:
Ta thấy hai đường thẳng xy và ab cắt nhau tại M nên đáp án C đúng.
Đáp án cần chọn là: C
Câu 15. Cho hình vẽ sau. Chọn câu đúng.
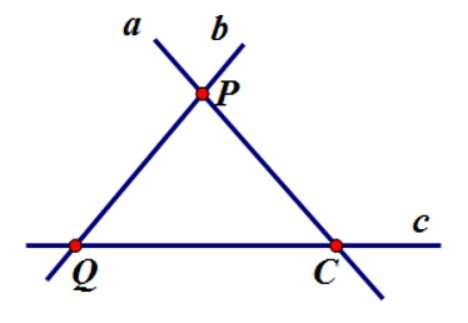
A.
B.
C. Đường thẳng a cắt đường thẳng c tại điểm P
D. Không có hai đường thẳng nào cắt nhau trên hình vẽ
Đáp án: B
Giải thích:
Từ hình vẽ ta thấy nên đáp án A sai; nên đáp án B đúng.
Hai đường thẳng a và c cắt nhau tại điểm C nên đáp án C sai.
Đáp án D sai vì ta thấy có ba cặp đường thẳng cắt nhau trên hình vẽ là a và c, a và b, b và c.
Đáp án cần chọn là: B
Câu 16. Cho hai tia Ox và Oy đối nhau. Lấy điểm G trên tia Ox, điểm H trên tia Oy. Ta có:
A. Điểm G nằm giữa hai điểm O và H
B. Điểm O nằm giữa hai điểm G và H
C. Điểm H nằm giữa hai điểm O và G
D. Không có điểm nào nằm giữa hai điểm còn
Đáp án: B
Giải thích:

Ta có Ox và Oy là hai tia đối nhau và G thuộc tia Ox, H thuộc tia Oy nên điểm O nằm giữa hai điểm G và H.
Câu 17. Vẽ ba đường thẳng phân biệt bất kì, số giao điểm của ba đường thẳng đó không thể là:
A. 0
B. 1 hoặc 2
C. 4
D. 3
Đáp án: C
Giải thích:
Với 3 đường thẳng phân biệt ta có các trường hợp sau:
+ Không có đường thẳng nào cắt nhau nên không có điểm chung.
+ Hai đường thẳng cắt nhau, đường thẳng còn lại không cắt hai đường thẳng đó, khi đó có 1 điểm chung.
+ Ba đường thẳng đó có đôi một cắt nhau thì có ba điểm chung.
Vậy không thể có trường hợp ba đường thẳng phân biệt bất kì mà có 4 điểm chung.
Đáp án cần chọn là: C
Câu 18. Cho hình vẽ. Em hãy chọn khẳng định sai:

A. NM và NI là hai tia đối nhau
B. IN và IM là hai tia trùng nhau
C. MN và MI là hai tia trùng nhau
D. MN và NI là hai tia trùng nhau
Đáp án: D
Giải thích:
Từ hình vẽ ta thấy các điểm M, N, I cùng thuộc một đường thẳng.
+) Hai tia NM và NI đối nhau vì chúng chung gốc N và tạo thành một đường thẳng, từ đó loại đáp án A.
+) Hai tia IN và IM trùng nhau vì chúng chung gốc I và có thêm điểm chung là N, từ đó loại đáp án B.
+) Hai tia MN và MI trùng nhau vì chúng chung gốc M và có thêm điểm chung là N, từ đó loại đáp án C.
+) Hai tia MN và NI không trùng nhau vì chúng không chung gốc.
Đáp án cần chọn là: D
Câu 19. Cho L là điểm nằm giữa hai điểm I và K. Biết IL = 2cm, LK = 5cm. Độ dài của đoạn thẳng IK là:
A. 3cm
B. 2cm
C. 5cm
D. 7cm
Đáp án: D
Giải thích:

Vì L nằm giữa I và K nên ta có: IL + LK = IK ⇒ IK = 2 + 5 = 7cm
Đáp án cần chọn là: D
Câu 20. Lấy bốn điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng. Cứ qua hai điểm ta vẽ một đường thẳng. Số đường thẳng có thể vẽ được là:
A. 3
B. 10
C. 12
D. 4
Đáp án: B
Giải thích:
Từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được các đường thẳng đi qua hai điểm bất kì như sau:
+ Với điểm M ta có thể nối với các điểm: N, P, Q, K để tạo thành 4 đường thẳng phân biệt.
+ Với điểm N ta có thể nối với các điểm: P, Q, K để tạo thành 3 đường thẳng phân biệt.
+ Với điểm P ta có thể nối với các điểm: Q, K để tạo thành 2 đường thẳng phân biệt.
+ Với điểm Q ta có thể nối với điểm K để tạo thành 1 đường thẳng .
Vậy từ 5 điểm M, N, P, Q, K trong đó không có ba điểm nào thẳng hàng ta có thể vẽ được tất cả:
4 + 3 + 2 + 1 = 10 đường thẳng phân biệt.
Đáp án cần chọn là: B
Câu 21. Cho trước 6 điểm trong đó có 4 điểm thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng?
A. 15
B. 16
C. 14
D. 13
Đáp án: A
Giải thích:
Vì qua 2 điểm luôn vẽ được một đoạn thẳng
Nên qua 6 điểm vẽ được số đoạn thẳng là:
(đoạn thẳng)
Đáp án cần chọn là: A
Phần 2. Lý thuyết Chương 8: Những hình học cơ bản
1. Điểm thuộc, không thuộc đường thẳng
a) Điểm, đường thẳng
- Dùng bút chấm 1 chấm nhỏ cho ta một hình ảnh về điểm
- Dùng bút chì và thước thẳng, vẽ được một vạch thẳng cho ta hình ảnh về một đường thẳng.
- Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường thẳng.
b) Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
- Điểm thuộc đường thẳng nếu điểm đó nằm trên đường thẳng đó hay đường thẳng đó đi qua điểm đó.
- Điểm không thuộc đường thẳng nếu điểm đó không nằm trên đường thẳng hay đường thẳng đó không đi qua điểm đó.
- Ta dùng kí hiệu ∈ thể hiện điểm thuộc đường thẳng và ∉ để thể hiện điểm không thuộc đườn thẳng.
c) Đường thẳng đi qua hai điểm phân biệt
- Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt
2. Ba điểm thẳng hàng
- Ba điểm thẳng hàng là ba điểm thuộc cùng một đường thẳng.
3. Hai đường thẳng song song, cắt nhau, trùng nhau.
- Hai đường thẳng song song là hai đường thẳng không có điểm chung. Kí hiệu song song là //.
- Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.
- Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.
|
|
|
|
|
a và b song song với nhau kí hiệu: a // b |
a và b cắt nhau tại điểm E |
Đường thẳng AB và đường thẳng BC trùng nhau. |
4. Điểm nằm giữa hai điểm

+ Điểm B nằm giữa hai điểm A và C.
+ Hai điểm A và B nằm cùng phía đối với điểm C.
+ Hai điểm A và C nằm khác phía đối với điểm B.
5. Tia
a) Tia
Điểm O trên đường thẳng xy chia đường thẳng xy thành hai phần.
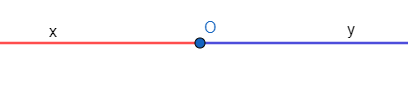
- Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O. Điểm O là gốc của tia.
b) Hai tia đối nhau
- Hai tia đối nhau là hai tia chung gốc và tạo thành một đường thẳng
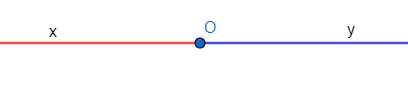
- Hai tia Ox và Oy là gọi là hai tia đối nhau (tia Ox là tia đối của tia Oy và tia Oy là tia đối của tia Ox).
c) Hai tia trùng nhau
- Hai tia trùng nhau là hai tia chung gốc và có thêm ít nhất 1 điểm chung khác điểm gốc
- Khi điểm B thuộc tia Am thì tia Am còn được gọi là tia AB, khi đó tia Am và tia AB được gọi là trùng nhau.

6. Đoạn thẳng
- Đoạn thẳng AB, hay đoạn thẳng BA, là hình gồm 2 điểm A, B cùng với tất cả các điểm nằm giữa A và B.
- A; B là hai đầu mút (mút) của đoạn thẳng AB.
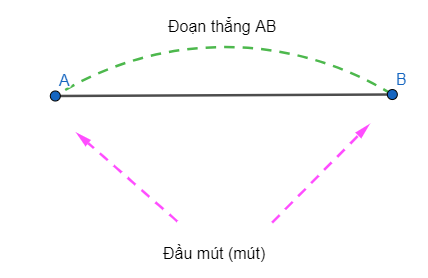
7. Độ dài đoạn thẳng
a) Độ dài đoạn thẳng
- Mỗi đoạn thẳng có một độ dài. Khi chọn một đơn vị độ dài thì độ dài mỗi đoạn thẳng được biểu diễn bởi một số dương (thường viết kèm đơn vị).
- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. Ta quy ước khoảng cách giữa hai điểm trùng nhau bằng 0 (đơn vị).
- Đơn vị đo độ dài đoạn thẳng: mm; cm; dm; m; km…
b) So sánh độ dài đoạn thẳng
- Hai đoạn thẳng AB và EG có cùng độ dài. Ta viết AB = EG và nói đoạn thẳng AB bằng đoạn thẳng EG.

- Đoạn thẳng AB có độ dài nhỏ nhơn đoạn thẳng CD. Ta viết AB < CD và nói AB ngắn hơn CD hoặc CD > AB và nói CD dài hơn AB.

c) Đo độ dài đoạn thẳng
Để đo độ dài đoạn thẳng ta làm như sau:
Bước 1: Đặt thước trùng với đường thẳng sao cho vạch 0 của thước trùng với một đầu mút của đoạn thẳng.
Bước 2: Quan sát xem đầu mút còn lại trùng với vạch mấy của thước thì số chỉ ở vạch đó chính là độ dài đoạn thẳng.
Chú ý: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB
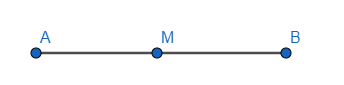
8. Trung điểm của đoạn thẳng
- Nếu điểm I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB.
Khi đó:
IA = IB = 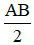 .
.

9. Góc
- Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc.
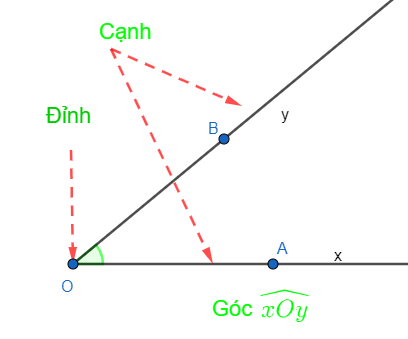
+ Góc xOy, kí hiệu 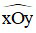 (hoặc ∠xOy ) gồm hai tia chung gốc Ox và Oy.
(hoặc ∠xOy ) gồm hai tia chung gốc Ox và Oy.
+ Điểm O là đỉnh của góc xOy. Hai tia Ox; Oy là các cạnh của góc xOy.
+ Góc xOy còn có các cách gọi khác là góc AOB; góc O; góc yOx; góc BOA.
+ Đặt biệt khi Ox và Oy là hai tia đối nhau, ta có góc bẹt xOy.
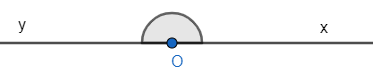
10. Điểm trong của góc
Quan sát hình vẽ:
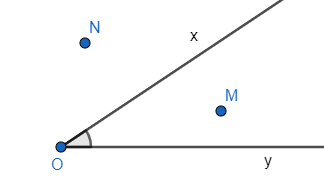
- Ta gọi M là một điểm trong của góc xOy (điểm M nằm trong góc xOy).
- Các điểm nằm trên hai cạnh của góc và các điểm như điểm N không phải là điểm trong góc xOy.
11. Đo góc
- Muốn đo 1 góc xOy, ta đặt thước đo góc sao cho tâm của thước trùng với O, tia Ox đi qua vạch 0. Khi đó tia Oy đi qua vạch chỉ số đo của góc.
12. Các góc đặc biệt
- Góc có số đo bằng 90o là góc vuông.
- Góc bẹt là góc có số đo bằng 180o.
- Góc nhỏ hơn góc vuông là góc nhọn.
- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù.
|
Góc vuông |
Góc nhọn |
Góc tù |
Góc bẹt |
|
|
|
|
|
|
∠xAy = 90o |
0o < ∠xAy < 90o |
90o < ∠xAy < 180o |
∠xAy = 180o |
Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:
Chương 4: Một số hình phẳng trong thực tiễn
Chương 5: Tính đối xứng của hình phẳng trong tự nhiên