Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 6 Chương 5: Tính đối xứng của hình phẳng trong tự nhiên sách Kết nối tri thức. Tài liệu gồm 15 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:

Trắc nghiệm Toán lớp 6 Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

Phần 1. Trắc nghiệm Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

I. Nhận biết

Câu 1. Cho hình vẽ:

Hình vẽ nào dưới đây biểu diễn tất cả trục đối xứng của hình vẽ trên:

A.

B.

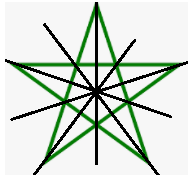
C.

D.

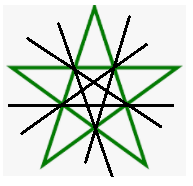
Lời giải

Hình biểu diễn tất cả các trục đối xứng của hình đã cho là:

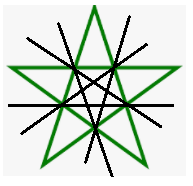
Chọn B.

Câu 2. Trong các phát biểu sau, có bao nhiêu phát biểu đúng?

a) Số trục đối xứng của tam giác đều nhỏ hơn số trục đối xứng của hình thoi.

b) Hình tròn có một trục đối xứng là đường thẳng đi qua tâm của hình tròn.

c) Hình thang cân có tâm đối xứng là giao điểm của hai đường chéo.

d) Hình chữ nhật có hai trục đối xứng là hai đường chéo.

A. 0

B. 2

C. 3

D. 4

Lời giải

Tam giác đều có 3 trục đối xứng, hình thoi có 2 trục đối xứng nên a) sai.

Hình tròn có vô số trục đối xứng là các đường thẳng đi qua tâm nên b) sai.

Hình thang cân không có tâm đối xứng nên c) sai.

Hình chữ nhật có hai trục đối xứng là hai đường thẳng nối trung điểm của hai cạnh đối diện nên d) sai.

Vậy không có phát biểu nào đúng.

Chọn A

Câu 3. Trong các hoa văn sau, hình hoa văn nào có tâm đối xứng?

A. Hình a) và hình b)

B. Hình b) và hình c)

C. Hình c) và hình a)

D. Không có hình nào

Lời giải

Hình a) và hình c) có tâm đối xứng

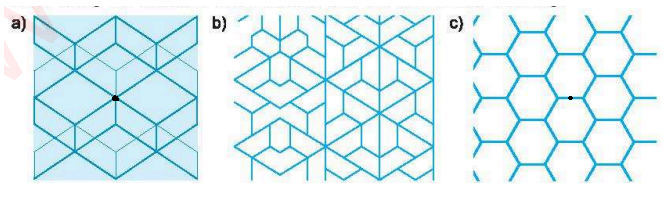
Chọn C

Câu 4. Trong các câu sau, câu nào sai?

A. Hình lục giác đều có 6 tâm đối xứng.

B. Hình tròn có một tâm đối xứng là tâm của đường tròn

C. Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo

D. Hình thang cân không có tâm đối xứng.

Lời giải

Hình lục giác đều chỉ có 1 tâm đối xứng là giao điểm của ba đường chéo. Do đó A sai.

Chọn A

Câu 5. Hình vẽ nào dưới đây biểu diễn đúng trục đối xứng của hình sau:

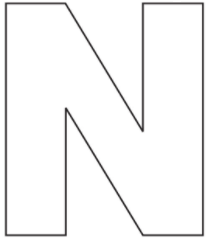
A.

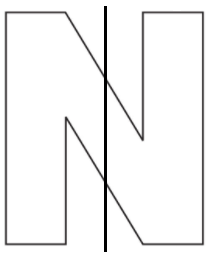
B.

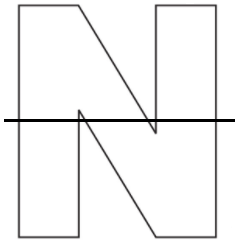
C. Hình này không có trục đối xứng

D.

Lời giải

Hình đã cho không có trục đối xứng.

Chọn C

Câu 6. Trong các câu sau, câu nào đúng?

A. Tam giác đều có 6 trục đối xứng

B. Hình chữ nhật với hai kích thước khác nhau có 4 trục đối xứng

C. Hình thang cân, góc ở đáy khác 90⁰, có đúng một trục đối xứng

D. Hình bình hành có hai trục đối xứng.

Lời giải

- Tam giác đều có 3 trục đối xứng nên A sai.

- Hình chữ nhật với hai kích thước có 2 trục đối xứng nên B sai.

- Hình thang cân, góc ở đáy khác 90⁰, có đúng 1 trục đối xứng nên C đúng.

- Hình bình hành không có trục đối xứng nên D sai.

Chọn D

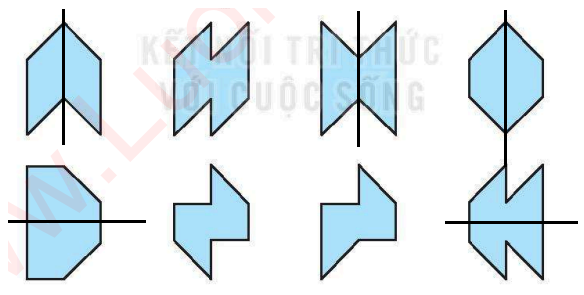
Câu 7. Quan sát các hình dưới đây:

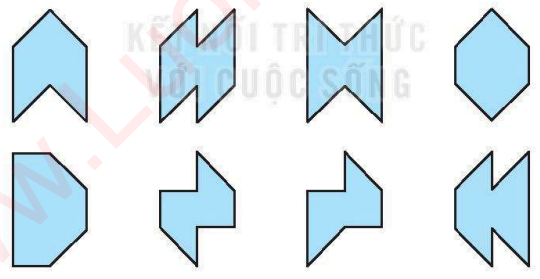
Có bao nhiêu hình có trục đối xứng

A. 3

B. 4

C. 5

D. 6

Lời giải

Có 5 hình có trục đối xứng

Câu 8. Cho các hình vẽ dưới đây

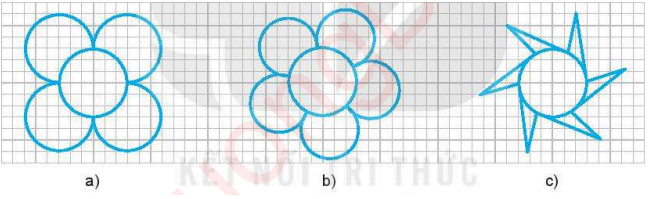
Hình nào là hình có tâm đối xứng?

A. Hình a) và Hình b)

B. Hình a) và Hình c)

C. Hình b) và Hình c)

D. Cả ba Hình a), Hình b) và Hình c).

Lời giải

Hình a) và Hình c) là hình có tâm đối xứng.

Chọn B

Câu 9. Trong các câu sau, câu nào sai?

A. Hình vuông có 4 trục đối xứng.

B. Hình thoi, các góc khác 90⁰ có đúng hai trục đối xứng.

C. Hình lục giác đều có đúng 3 trục đối xứng.

D. Hình chữ nhật có hai kích thước khác nhau có đúng hai trục đối xứng.

Lời giải

Hình lục giác đều có tất cả 6 trục đối xứng

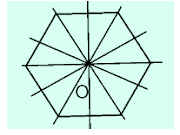
Do đó C sai.

Chọn C

Câu 10. Trong các biểu tượng sau, biểu tượng nào có trục đối xứng?

A. Biểu tượng hòa bình và biểu tượng Hội chữ thập đỏ

B. Biểu tượng Hội chữ thập đỏ và biểu tượng ngành Y dược

C. Biểu tượng ngành Y dược và biểu tượng hòa bình

D. Cả ba biểu tượng trên

Lời giải

Có hai biểu tượng có trục đối xứng là: biểu tượng hòa bình và biểu tượng Hội chữ thập đỏ.

Chọn A

II. Thông hiểu

Câu 1. Đoạn thẳng AB có độ dài 4cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn OA.

A. 8 cm

B. 1 cm

C. 2 cm

D. 4 cm

Lời giải

Do O là tâm đối xứng của AB nên O chia đoạn thẳng AB thành hai đoạn OA bằng OB và bằng một nửa AB bằng 2cm.

Chọn C

Câu 2. Cho hình bình hành ABCD có tâm O là tâm đối xứng. Biết OA = 5cm, OD = 7cm, tính độ dài hai đường chéo AC và BD

A. 5cm, 7cm

B. 5cm, 14cm

C. 10cm, 7cm

D. 10cm, 14cm

Lời giải

Do O là tâm đối xứng nên O là giao điểm của hai đường chéo và thỏa mãn OA bằng OC, OB bằng OD.

Suy ra độ dài AC gấp đôi độ dài OA bằng 5.2 = 10cm,

Độ dài BD gấp đôi độ dài OD bằng 7.2 = 14cm.

Vậy AC = 10cm, BD = 14cm.

Chọn D

Câu 3. Hình thoi ABCD có tâm đối xứng O. Biết OA = 3cm, OB = 2cm. Hãy tính diện tích hình thoi.

A. 6 cm²

B. 12 cm²

C. 24 cm²

D. 48 cm²

Lời giải

Vì O là tâm đối xứng nên độ dài AC gấp đôi độ dài OA bằng 6cm và độ dài BD gấp đôi độ dài OB bằng 4cm.

Diện tích hình thoi ABCD là: 6.4:2= 12 cm².

Chọn B

Câu 4. Một chiếc bàn có mặt bàn là hình lục giác đều như hình dưới đây. Biết rằng độ dài đường chéo chính là 1,2m, em hãy tích khoảng cách từ tâm đối xứng của mặt bàn đến mỗi đỉnh và chu vi mặt bàn.

A. 1,2 m và 7,2 m

B. 0,6 m và 7,2 m

C. 0,6 m và 3,6 m

D. 1,2 m và 3,6 m

Lời giải

Khoảng cách từ tâm đối xứng đến mỗi đỉnh bằng một nửa đường chéo chính và bằng: 1,2:2 = 0,6 (m).

Do hình lục giác đều được ghép từ 6 tam giác đều nên cạnh của hình lục giác cũng bằng 0,6 (m).

Chu vi mặt bàn là: 0,6.6 = 3.6 (m).

Chọn C

Câu 5. Một hình tròn có bán kính 6cm, khoảng cách từ tâm đối xứng đến các điểm nằm trên đường tròn bằng:

A. 3cm

B. 2cm

C. 6cm

D. 12cm

Lời giải

Tâm đối xứng của hình tròn chính là tâm của đường tròn nên khoảng cách từ tâm đối xứng đến các điểm trên đường tròn đúng bằng bán kính và bằng 6cm.

Chọn C

Phần 2. Lý thuyết Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

1. Hình có trục đối xứng trong thực tế

Các hình có một đường thẳng d chia hình đó thành hai phần mà nếu “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau. Những hình như thế được gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.

2. Trục đối xứng của một số hình phẳng

Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn. Do đó hình tròn có vô số trục đối xứng.

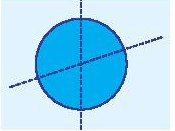
Mỗi đường chéo là một trục đối xứng của hình thoi.

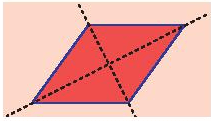
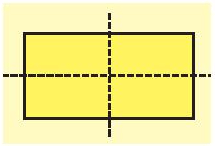
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.

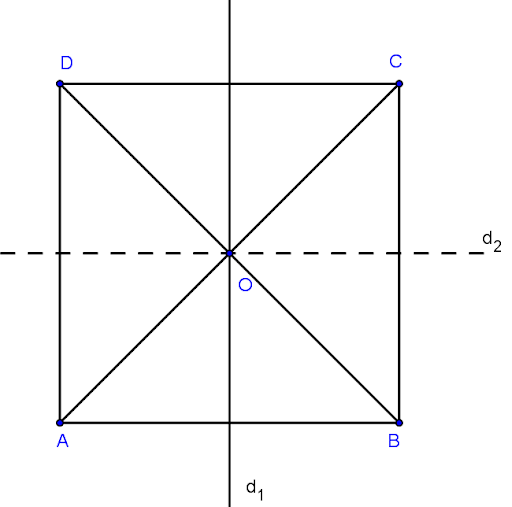
Hình vuông có 4 trục đối xứng bao gồm: Hai đường thẳng đi qua trung điểm hai cạnh đối điện và hai đường chéo.

3. Hình có tâm đối xứng trong thực tế

Mỗi hình có mổ điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được “trùng khít” với chính nó ở vị trí ban đầu (trước khi quay).

Những hình như thế được gọi là “hình có tâm đối xứng” và điểm O được gọi là “tâm đối xứng” của hình.

4. Tâm đối xứng của một số hình phẳng

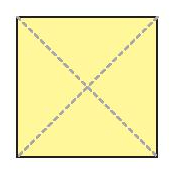
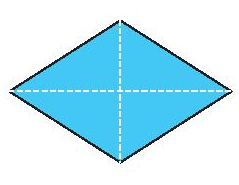
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.

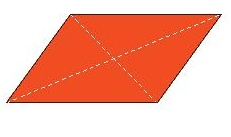
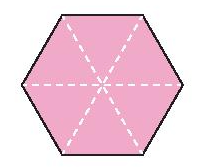
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.

Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:

Chương 4: Một số hình phẳng trong thực tiễn

Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

Chương 6: Phân số

Chương 7: Số thập phân

Chương 8: Những hình học cơ bản