Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 6 Chương 7: Số thập phân sách Kết nối tri thức. Tài liệu gồm 12 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:

Trắc nghiệm Toán lớp 6 Chương 7: Số thập phân

Phần 1. Trắc nghiệm Chương 7: Số thập phân

Câu 1. Trên đĩa có 64 quả táo. Hoa ăn hết 25% số táo. Sau đó Hùng ăn $\frac{3}{8}$ số táo còn lại. Hỏi trên đĩa còn bao nhiêu quả táo?

A. 30 quả

B. 48 quả

C. 18 quả

D. 36 quả

Trả lời:

Hoa ăn số táo là 

25%.64 = 16 quả.

Số táo còn lại là 

64 – 16 = 48 quả

Hùng ăn số táo là $\frac{3}{8}.48=18$ quả.

Số táo còn lại sau khi Hùng ăn là 

48 – 18 = 30 quả.

Đáp án cần chọn là: A

Câu 2. Lớp 6A có 48  học sinh. Số học sinh giỏi bằng 18,75%  số học sinh cả lớp. Số học sinh trung bình bằng  300% số học sinh giỏi. Còn lại là học sinh khá. Tính tỉ số phần trăm số học sinh giỏi so với số học sinh khá.

A. 50%

B. 125%

C. 75%

D. 70%

Trả lời:

Số học sinh giỏi của lớp là 

18,75%.48 = 9 học sinh

Số học sinh trung bình là 

9.300% = 27 học sinh

Số học sinh khá là 

48 – 9 – 27 = 12 học sinh

Tỉ số phần trăm số học sinh khá và số học sinh giỏi là: $\frac{9}{12}.100\%=75\%$

Đáp án cần chọn là: C

Câu 3. Một nhà máy có ba phân xưởng, số công nhân của phân xưởng 1 bằng 36% tổng số công nhân của nhà máy. Số công nhân của phân xưởng 2 bằng $\frac{3}{5}$ số công nhân của phân xưởng 3. Biết số công nhân của phân xưởng 1 là 18 người. Tính số công nhân của phân xưởng 3.

A. 12

B. 20

C. 18

D. 25

Trả lời:

Số công nhân của cả nhà máy là 

18:36% = 50 công nhân

Số công nhân của phân xưởng 2 và phân xưởng 3 là 

50 – 18 = 32 công nhân

Vì số công nhân của phân xưởng 2 bằng $\frac{3}{5}$ số công nhân của phân xưởng 3 nên số công nhân của phân xưởng 2 bằng $\frac{3}{3+5}=\frac{3}{8}$ số công nhân của cả hai phân xưởng.

Số công nhân của phân xưởng 2 là $32.\frac{3}{8}=12$ ông nhân

Số công nhân của phân xưởng ba là 

32 – 12 = 20 công nhân

Đáp án cần chọn là: B

Câu 4. Người ta mở vòi cho nước chảy vào đầy bể cần 3 giờ. Hỏi nếu mở vòi nước đó trong 45 phút thì được bao nhiêu phần của bể?

A.$\frac{1}{3}$

B.$\frac{1}{4}$

C.$\frac{2}{3}$

D.$\frac{1}{2}$

Trả lời:

Đổi: 45phút = $\frac{3}{4}$ giờ

Mỗi giờ vòi nước chảy được số phần bể là: $1:3=\frac{1}{3}$ (bể)

Nếu mở vòi trong 45 phút thì được số phần bể là: $\frac{3}{4}.\frac{1}{3}=\frac{1}{4}$ (bể)

Đáp án cần chọn là: B

Câu 5. Lúc 7 giờ 5 phút, một người đi xe máy đi từ A và đến B lúc 8 giờ 45 phút. Biết quãng đường AB dài 65km. Tính vận tốc của người đi xe máy đó?

A. 39 km/h

B. 40 km/h

C. 42 km/h

D. 44 km/h

Trả lời:

Thời gian người đó đi hết quãng đường AB là:

8 giờ 45 phút – 7 giờ 5 phút = 1 giờ 40 phút

Đổi 1 giờ 40 phút =   giờ.

Vận tốc của người đi xe máy đó là: $65:\frac{5}{3}=39$ (km/h)65:53=39(km/h)

Đáp án cần chọn là: A

Câu 6. Cho $A=\frac{\left(3\frac{2}{15}+\frac{1}{5}\right):2\frac{1}{2}}{\left(5\frac{3}{7}-2\frac{1}{4}\right):4\frac{43}{56}}$ và $B=\frac{\mathrm{1,2}:\left(1\frac{1}{5}.1\frac{1}{4}\right)}{\mathrm{0,32}+\frac{2}{25}}$ . Chọn đáp án đúng

A. A < - B

B. 2A > B

C. A > B

D. A = B

Trả lời:

Ta có:

$$\begin{gathered} A=\frac{\left(3\frac{2}{15}+\frac{1}{5}\right):2\frac{1}{2}}{\left(5\frac{3}{7}-2\frac{1}{4}\right):4\frac{43}{56}}=\frac{\left(\frac{47}{15}+\frac{3}{15}\right):\frac{5}{2}}{\left(\frac{38}{7}-\frac{9}{4}\right):\frac{267}{56}}=\frac{\frac{50}{15}.\frac{2}{5}}{\left(\frac{152}{28}-\frac{63}{28}\right).\frac{56}{267}}=\frac{\frac{4}{3}}{\frac{89}{28}.\frac{56}{267}} \\ =\frac{\frac{4}{3}}{\frac{2}{3}}=2 \end{gathered}$$

$B=\frac{\mathrm{1,2}:\left(1\frac{1}{5}.1\frac{1}{4}\right)}{\mathrm{0,32}+\frac{2}{25}}=\frac{\frac{6}{5}:\left(\frac{6}{5}.\frac{5}{4}\right)}{\frac{8}{25}+\frac{2}{25}}=\frac{\frac{6}{5}:\frac{3}{2}}{\frac{10}{25}}=\frac{\frac{4}{5}}{\frac{2}{5}}=2$

Vậy A = B

Đáp án cần chọn là: D

Câu 7. Phân số $\frac{2}{5}$ viết dưới dạng số thập phân là:

A. 2,5

B. 5,2

C. 0,4

D. 0,04

Trả lời:

$\frac{2}{5}=\frac{4}{10}=\mathrm{0,4}$

Đáp án cần chọn là: C

Câu 8. Hỗn số $1\frac{2}{5}$  được chuyển thành số thập phân là:

A. 1,2

B. 1,4

C. 1,5

D. 1,8

Trả lời:

$1\frac{2}{5}=\frac{1.5+2}{5}=\frac{7}{5}=\frac{14}{10}=\mathrm{1,4}$

Đáp án cần chọn là: B

Câu 9. Số thập phân 3,015 được chuyển thành phân số là:

A.$\frac{3015}{10}$

B.$\frac{3015}{100}$

C.$\frac{3015}{1000}$

D.$\frac{3015}{10000}$

Trả lời:

$\mathrm{3,015}=\frac{3015}{10}$

Đáp án cần chọn là: C

Câu 10. Số tự nhiên x thỏa mãn: 35,67 < x < 36,05 là:

A. 35

B. 36

C. 37

D. 34

Trả lời:

Ta có: 35,67 < x < 36,05 và xx là số tự nhiên nên x = 36.

Đáp án cần chọn là: B

Câu 11. Tìm x, biết: $\mathrm{2,4}x=\frac{-6}{5}\mathrm{.0,4}$

A. x = 4

B. x = −4

C. x = 5

D. x = −0,2

Trả lời:

$\mathrm{2,4}x=\frac{-6}{5}\mathrm{.0,4}$

2,4.x = −1,2.0,4

2,4.x = −0,48

x = −0,48:2,4

x = −0,2

Đáp án cần chọn là: D

Câu 12. Một người gửi tiết kiệm 15.000.000 đồng với lãi suất 0,6% một tháng thì sau một tháng người đó thu được tất cả bao nhiêu tiền?

A. 15.090.000 đồng

B. 15.080.000 đồng

C. 15.085.000 đồng

D. 15.100.000 đồng.

Trả lời:

Tiền lãi thu được sau 1 tháng là:  

15.000.000 : 100 × 0,6 = 90.000 đồng.

Tổng số tiền thu được sau 1 tháng là:  

15.000.000 + 90.000 = 15.090.000 đồng.

Đáp án cần chọn là: A

Phần 2. Lý thuyết Chương 7: Số Thập Phân

1. Phân số thập phân và số thập phân

a) Phân số thập phân.

– Phân số thập phân là phân số có phần mẫu số là lũy thừa của 10

b) Số thập phân

Ta viết   = –2, 8 là số thập phân âm, đọc là “âm một phẩy bốn”.

Ta viết 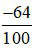  = –0, 64 là số thập phân âm, đọc là “âm không phẩy hai mươi lăm”.

c) Tính chất của số thập phân

- Mỗi số thập phân gồm: Phần số nguyên viết bên trái dấu “,”; phần thập phân viết bền phải dấu “,”.

- Nếu thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì số thập phân không đổi: 

21, 45 = 21, 450 = 21, 4500 = …

- Hai số thập phân được gọi là đối nhau nếu tổng của chúng bằng 0.

d) Đổi từ số thập phân ra phân số và ngược lại.

– Đổi từ số thập phân sang phân số ta làm như sau:

Bước 1: Đếm xem có bao nhiêu số ở phía bên phải dấu phẩy. Gọi n là số chữ số ở phía bên phải dấu phẩy.

Bước 2: Viết số không có dấu phẩy ở tử số và lũy thừa 10ⁿ ở mẫu số.

Bước 3: Rút gọn phân số phía trên để được phân số tối giãn.

– Đổi phân số ra số thập phân

Bước 1: Đưa phân số về dạng phân số thập phân có mẫu là lũy thừa của 10

Bước 2: Kiểm tra xem mẫu số là lũy thừa mấy của 10. Giả xử mẫu số là lũy thừa bậc n của 10.

Bước 3: Đếm từ phải sang tới số thứ n của tử và đặt dấu phẩy ở đó số thập phân cần tìm là số ở tửu đã được thêm dấu phẩy.

2. So sánh hai số thập phân

a) So sánh hai số thập phân dương

Muốn so sánh hai số thập phân ta có thể làm như sau:

– So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

– Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

– Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

b) So sánh hai số thập phân âm

– Nếu a, b là hai số thập phân dương và a > b thì –a < –b

Chú ý: Số thập phân âm luôn nhỏ hơn 0 và nhỏ hơn số thập phân dương.

Số thập phân dương luôn lớn hơn 0 và lớn hơn số thập phân âm.

3. Phép cộng, trừ số thập phân

– Muốn cộng hai số thập phân âm, ta cộng hai số đối của của chúng và đặt dấu trừ đằng trước.

(–a) + (–b) = – (a + b) với a, b > 0

– Muốn cộng hai số thập phân khác dấu ta làm như sau: 

+ Nếu 0 < a b thì (–a) + b = b – a

+ Nếu a > b > 0 thì (–a) + b = –(a – b)

– Tương tự với phép cộng của số nguyên và phép cộng của phân số, phép cộng hai số thập phân cũng có các tính chất giao hoán, tính chất kết hợp, tính chất cộng với số 0.

Cho a, b, c là ba số thập phân khi đó ta có: 

Tính chất giao hoán: a + b = b + a

Tính chất kết hợp: (a + b) + c = a + (b + c)

Tính chất cộng với số 0: a + 0 = 0 + a = a.

– Phép trừ hai số thập phân được đưa về phép cộng hai số đối:

a – b  = a + (–b)

4. Phép nhân số thập phân

Ta thực hiện phép nhân hai số thập phân theo quy tắc tương tự như phép nhân hai số nguyên.

– Nhân hai số cùng dấu: (–a).(–b) = a.b  với a, b > 0

– Nhân hai số khác dấu: (–a).b = a.(–b) = – (a.b) với a, b > 0

– Tương tự với phép nhân số nguyên và phép nhân phân số, phép nhân các số thập phân cũng có các tính chất giao hoán, tính chất kết hợp, tính chất nhân với 1, tính chất phân phối của phép cộng và phép nhân.

Cho ba số thập phân a, b, c ta có: 

– Tính chất giao hoán: a.b = b.a

– Tính chất kết hợp: (a.b).c = a.(b.c)

– Tính chất nhân với số 1: a.1 = 1. a = a

– Tính chất phân phối giữa phép cộng và phép nhân: (a + b).c = a.c + b.c

5. Phép chia số thập phân

Ta thực hiện phép chia hai số thập phân theo quy tắc tương tự như phép chia hai số nguyên.

– Chia hai số nguyên cùng dấu:

(–a) : (–b) = a : b với a, b > 0

– Chia hai số nguyên khác dấu:

(–a) : b = a : (–b) = –(a:b) với a, b > 0

6. Làm tròn số

Để làm tròn một số thập phân dương đến một hàng nào đấy (gọi là hàng làm tròn), ta làm như sau: 

– Đối với chữ số hàng làm tròn:

+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hay bằng 5.

– Đối với các chữ số sau hàng làm tròn:

+ Bỏ đi nếu ở phần thập phân

+ Thay bởi các chữ số 0 nếu ở phần số nguyên.

7. Ước lượng

Trong đời sống, đôi khi ta không quá quan tâm đến tính chính xác của kết quả mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát với kết quả nhất. Để làm được việc ngày ta thường sẽ ước lượng các giá trị để có được kết quả ước lượng.

Có thể ước lượng kết quả bằng một trong các cách sau:

– Cắt bỏ bớt một hay nhiều chữ số ở phần thập phân của kết quả;

– Làm tròn kết quả tới một hàng thích hợp;

– Làm tròn các số hạng, thừa số, số bị chia, số chia có trong dãy phép tính cần thực hiện.

8. Tỉ số và tỉ số phần trăm

– Tỉ số của số a và số b là thương của phép chia a cho b, được viết là a : b (với b khác 0)

Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số hai số đo cùng hai đại lượng đó.

9. Hai bài toán về tỉ số phần trăm

Bài 1: Tìm giá trị phần trăm của một số cho trước.

Muốn tìm m % của một số a đã cho ta tính a .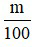 

Bài 2: Tìm một số biết giá trị phần trăm của số đó: 

Muốn tìm một số khi biết m % của số đó bằng b ta tính b :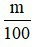

Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:

Chương 4: Một số hình phẳng trong thực tiễn

Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

Chương 6: Phân số

Chương 7: Số thập phân

Chương 8: Những hình học cơ bản