Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Đường trung bình của tam giác, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Đường trung bình của tam giác. Mời các bạn đón xem:

Bài tập Toán 8 Đường trung bình của tam giác

A. Bài tập Đường trung bình của tam giác

Bài 1: Tính độ dài đoạn AE, biết DE // BC và AC = 8 cm.

Hướng dẫn giải

Xét tam giác ABC, ta có: D là trung điểm AB và DE // BC

⇒ E là trung điểm của AC.

Suy ra: AE = $\frac{1}{2}AC=\frac{1}{2}\cdot 8=4cm$ .

Bài 2: Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = $\frac{1}{2}$  DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh: AI = IM.

Hướng dẫn giải

Gọi E là trung điểm của DC.

Trong ΔBDC, ta có:

M là trung điểm của BC (giả thiết).

E là trung điểm của CD (ta gọi).

Nên ME là đường trung bình của ∆BCD.

⇒ ME // BD (tính chất đường trung bình tam giác).

Suy ra: DI // ME.

Lại có: AD = $\frac{1}{2}$  DC (giả thiết).

DE = $\frac{1}{2}$ DC (vì E là trung điểm của DC).

Suy ra AD = DE nên D là trung điểm của AE.

Xét tam giác AME có D là trung điểm của AE và DI // ME (cmt).

Suy ra I là trung điểm của AM (tính chất đường trung bình của tam giác)

Vậy AI = IM.

Bài 3: Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC, F là trung điểm của EC. Tính tỉ số $\frac{AE}{EC}$ .

Hướng dẫn giải

Xét ∆BEC có:

M là trung điểm của BC;

F là trung điểm của EC.

Do đó, MF là đường trung bình của ∆BEC.

Suy ra MF // BE.

Xét ∆AMF có:

D là trung điểm của AM;

DE // MF (do MF // BE).

Do đó, DE là đường trung bình của ∆AMF.

Suy ra E là trung điểm của AF nên AE = EF.

Mà EF = FC = $\frac{1}{2}$ EC (do F là trung điểm của EC)

Do vậy, AE = EF = FC = $\frac{1}{2}$ EC.

Suy ra $\frac{AE}{EC}=\frac{1}{2}$ .

Bài 4: Cho tam giác ABC, có AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao cho AD = DE = EB. Đoạn CD cắt AM tại I. Chứng minh:

a) EM song song với DC;

b) I là trung điểm AM;

c) DC = 4DI.

Lời giải:

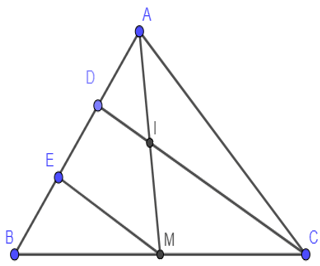
a) Vì ED = EB nên E là trung điểm của BD

Lại có M là trung điểm của BC 

Suy ra EM là đường trung bình của tam giác BCD

=> EM // CD

b) Xét tam giác AEM có:

 Ta có: AD = DE nên D là trung điểm AE.

Lại có I ∈ DC => DI // EM (do DC // EM)

Do đó: DI đi qua trung điểm AM

=> I là trung điểm của AM

c) Từ câu a ta có: EM là đường trung bình của tam giác BCD

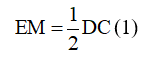
Lại có I là trung điểm của AM, D là trung điểm của AE 

=> DI là đường trung bình của tam giác AEM

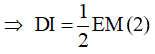
Từ (1) và (2) =>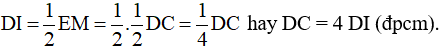 

*Bài tập tự luyện

Bài 1: Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:

a) EF là đường trung bình của tam giác ABC;

b) AM là đường trung trực của EF.

Bài 2: Cho tam giác ABC có AM là trung tuyến ứng với cạnh BC. Trên cạnh AC lấy điểm D sao cho 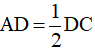 . Kẻ Mx song song song với BD và cắt AC tại E. Đoạn BD cắt AM tại I. Chứng minh:

a) AD = DE = EC;

b) S_AIB = S_IBM ;

c) S_ABC = S_IBC .

Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Từ H kẻ Hx vuông góc với AB tại P, Hy vuông góc với AC tại Q. Trên các tia Hx, Hy lần lượt lấy các điểm D và E sao cho PH = PD; QH = QE. Chứng minh:

a) A là trung điểm của DE;

b)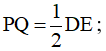 

c) PQ = AH.

Bài 4: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE // IK; DE = IK.

Bài 5: Cho tam giác ABC vuông cân tại A. Trên các cạnh góc vuông AB, AC lấy D và E sao cho AD = AE. Qua D kẻ đường thẳng vuông góc với BE cắt BC ở K. Qua A kẻ đường thẳng vuông góc với BE cắt BC ở H. Gọi M là giao điểm của DK và AC. Chứng minh:

a) Tam giác BAE bằng tam giác CAD;

b) Tam giác MDC cân;

c) HK = HC. 

Bài 6: Cho tam giác ABC. Trên tia đối của tia BC lấy điểm M sao cho BM = AB . Trên tia đối của tia CM lấy điểm N sao cho CN = AC. Gọi P là chân đường vuông góc kẻ từ M đến AM, Q là chân đường vuông góc kẻ từ C đến AN. Chứng minh rằng PQ song song với MN.

Bài 7: Cho tam giác ABC vuông tại A, đường cao AH. Gọi E là trung điểm của HC, F là trung điểm của AH. Chứng minh BF ⊥ AE.

Bài 8: Cho tam giác ABC, điểm A không cố định. Dựng các tam giác BAD, ACE vuông cân tại B và C ở ngoài tam giác ABC. Chứng minh rằng khi A di chuyển thì DE luôn đi qua một điểm cố định.

B. Lý thuyết Đường trung bình của tam giác

1. Định nghĩa đường trung bình của tam giác

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Ví dụ: Chỉ ra các đường trung bình trong tam giác sau với D, E, F lần lượt là trung điểm của BC, AC, AB.

Hướng dẫn giải

Các đường trung bình của ∆ABC là DE, DF, EF.

2. Tính chất đường trung bình của tam giác

2.1. Tính chất đường trung bình của tam giác

Định lí: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.

2.2. Chứng minh định lí

Gọi M là trung điểm của BC.

Tam giác ABC có $\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{2}$ , suy ra DE // BC (định lí Thalès đảo).

Tương tự ta chứng minh được EM // AB.

Tứ giác DEMB có DE //BM và EM // DB nên tứ giác DEMB là hình bình hành (dấu hiệu nhận biết hình bình hành), suy ra DE = BM = $\frac{1}{2}BC$ .

Vậy DE // BC; DE = $\frac{1}{2}BC$ .

Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.

Ví dụ: Cho tam giác ABC với D, E lần lượt là trung điểm của AB, AC. Biết BC = 8 cm. Tính DE.

Hướng dẫn giải

Ta có tam giác ABC có D, E lần lượt là trung điểm của AB, AC.

Do đó, DE là đường trung bình của tam giác ABC.

Suy ra: DE = $\frac{1}{2}BC$  = $\frac{1}{2}.8$  = 4 (cm).

Vậy DE = 4 cm.