Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Hàm số bậc nhất y = ax + b (a ≠ 0), được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hàm số bậc nhất y = ax + b (a ≠ 0). Mời các bạn đón xem:

Bài tập Toán 8 Hàm số bậc nhất y = ax + b (a ≠ 0)

A. Bài tập Hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 1: Xác định các hệ số của x, hệ số tự do trong mỗi hàm số bậc nhất sau:

a) y = 3x – 4;

b) y = −x + 2;

c) $y=\frac{x}{2}$

Hướng dẫn giải

a) Hệ số của x là 3; hệ số tự do là −4.

b) Hệ số của x là −1; hệ số tự do là 2.

c) Hệ số của x là $\frac{1}{2}$ ; hệ số tự do là 0.

Bài 2: Cho hàm số bậc nhất f(x) = x −1. Tính f (1); f(0); f(−2).

Hướng dẫn giải

f(1) = 1 −1 = 0; f(0) = 0 −1 = −1; f(−2) = −2 −1 = −3.

Vậy f(1) = 0; f(0) = −1; f(−2) = −3.

Bài 3: Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22000 đồng/tháng và cước gọi là 800 đồng/phút.

a) Lập công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút?

b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút?

c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút?

Hướng dẫn giải

a) Công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút là: y = 800x + 22 000.

b) Số tiền cước điện thoại phải trả khi gọi 75 phút là:

y = 800 . 75 + 22 000 = 82 000 (đồng).

Vậy số tiền cước điện thoại phải trả khi gọi 75 phút là 82 000 đồng.

c) Số tiền cước điện thoại phải trả là 94000 đồng thì trong tháng đó thuê bao đã gọi số phút là:

94 000 = 800.x + 22 000

800x = 94 000 − 22 000  

800x = 72 000 

Do đó x = 90.

Vậy nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi 90 phút.

Câu 4: Lập phương trình đường thẳng đi qua hai điểm A(-1;2) và B(3;1).

Hướng dẫn giải

Giả sử phương trình đường thẳng cần tìm có dạng: y = ax + b (a#0).

Đường thẳng đi qua hai điểm A(-1;2), B(3;1) nên ta có:  .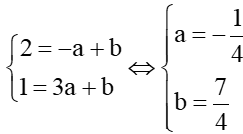

Vậy phương trình đường thẳng cần tìm là: y =.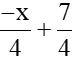

Câu 5: Tìm m để hàm số y = (3-m)x + 2 nghịch biến trên R.

Hướng dẫn giải

Hàm số y = (3-m)x + 2 có dạng hàm số bậc nhất.

Để hàm số nghịch biến trên R thì 3-m<0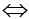m>3.

Câu 6: Tìm m để hàm số y = (m-1)x -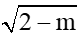 đồng biến trên R

Hướng dẫn giải

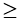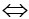Điều kiện xác định của hàm số là 2 - m0m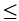2  (*).

Hàm số y = (m-1)x -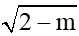có dạng hàm số bậc nhất nên hàm số đồng biến trên R khi m -1 > 0  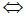m>1. Kết hợp với điều kiện (*), ta được 1<m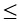2

Vậy với 1<m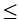2  thì hàm số đã cho đồng biến trên R

B. Lý thuyết Hàm số bậc nhất y = ax + b (a ≠ 0)

1. Định nghĩa

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax +b, trong đó a, b là các số cho trước và a khác 0.

Chú ý: Khi b = 0, ta có hàm số y = ax.

Ví dụ:

- Hàm số y = 2x + 3 là hàm số bậc nhất với hệ số a = 2; b = 3.

- Hàm số y = 4x là hàm số bậc nhất với hệ số a = 4; b = 0.

- Hàm số y = 0x – 1 không là hàm số bậc nhất vì a = 0.

2. Ứng dụng của hàm số bậc nhất

Ví dụ: Giá bán 1 kg vải thiều loại I là 35 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I. Hỏi y có phải là hàm số bậc nhất của x hay không?

b) Tính số tiền thu được khi bán 15 kg vải thiều loại I?

c) Cần bán bao nhiêu kg vải thiều loại I để thu được số tiền 1 400 000 đồng?

Hướng dẫn giải

a) Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là:

y = 35 000x.

Do đó y là hàm số bậc nhất của x.

b) Số tiền thu được khi bán 15 kg vải thiều loại I là:

35 000. 15 = 525 000 (đồng).

Vậy số tiền thu được khi bán 15 kg vải thiều loại I là 525 000 đồng.

c) Số kg vải thiều loại I để thu được số tiền 1 400 000 đồng là:

1 400 000 : 35 000 = 40 (kg).

Vậy cần bán 40 kg vải thiều loại I để thu được số tiền 1 400 000 đồng.