Với giải sách bài tập Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Giải SBT Toán 10 trang 23 Tập 1
Lời giải:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Xét miền nghiệm của bất phương trình x ≥ -1.
Vẽ đường thẳng d1: x = -1 bằng cách vẽ một đường thẳng song song với trục Oy tại một điểm có hoành độ bằng -1.
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x, ta có 1 > -1.
Suy ra miền nghiệm của bất phương trình x ≥ -1 là nửa mặt phẳng bờ d1 có chứa điểm I(1; 1).
• Xét miền nghiệm của bất phương trình y ≥ 0.
Đường thẳng d2: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d2 và thay vào biểu thức y, ta có 1 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d2 có chứa điểm I(1; 1).
• Xét miền nghiệm của bất phương trình x + y ≤ 4.
Vẽ đường thẳng d3: x + y = 4 bằng cách vẽ một đường thẳng qua hai điểm (0; 4) và (4; 0).
Chọn điểm I(1; 1) Ï d3 và thay vào biểu thức x + y = 4, ta có 1 + 1 = 2 < 4.
Suy ra miền nghiệm của bất phương trình x + y ≤ 4 là nửa mặt phẳng bờ d3 có chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây.
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x > 0 là nửa mặt phẳng bờ d1 có chứa điểm I(1;1) và bỏ đi đường thẳng d1.
• Đường thẳng y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d2 và thay vào biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y > 0 là nửa mặt phẳng bờ d2 có chứa điểm I(1;1) và bỏ đi đường thẳng d2.
• Vẽ đường thẳng d3: x - y - 4 = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; -4) và (4; 0).
Chọn điểm I(1; 1)∉ d3 và thay vào biểu thức x - y - 4 ta được 1 - 1 - 4 = -4 < 0.
Suy ra miền nghiệm của bất phương trình x - y - 4 < 0 là nửa mặt phẳng bờ d3 có chứa điểm I(1; 1) và bỏ đi đường thẳng d3.
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 3.
Chọn điểm O(0; 0) ∉ d1 và thay vào biểu thức y ta được 0 < 3.
Suy ra miền nghiệm của bất phương trình y ≤ 3 là nửa mặt phẳng bờ d1 có chứa điểm O(0; 0).
• Đường thẳng d2: x = 3 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 3.
Chọn điểm O(0; 0) ∉ d2 và thay vào biểu thức x ta được 0 < 3.
Suy ra miền nghiệm của bất phương trình x ≤ 3 là nửa mặt phẳng bờ d2 có chứa điểm O(0; 0).
• Đường thẳng d3: x = -1 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng -1.
Chọn điểm O(0; 0) ∉d3 và thay vào biểu thức x ta được 0 > -1.
Suy ra miền nghiệm của bất phương trình x ≥ -1 là nửa mặt phẳng bờ d3 có chứa điểm O(0; 0).
Đường thẳng d4: y = -2 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng -2.
Chọn điểm O(0; 0) ∉ d4 và thay vào biểu thức x ta được 0 > -2.
Suy ra miền nghiệm của bất phương trình y ≥ -2 là nửa mặt phẳng bờ d4 có chứa điểm O(0; 0).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Lời giải:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = 6 bằng cách vẽ đường thẳng đi qua hai điểm (6; 0) và (0; 6).
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x + y ta được 1 + 1 = 2 < 6.
Suy ra miền nghiệm của bất phương trình x + y ≤ 6 là nửa mặt phẳng bờ d1 có chứa điểm I(1; 1).
• Đường thẳng d2: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1) ∉d2 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d2 có chứa điểm I(1; 1).
• Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1)∉ d3 và thay vào biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d3 có chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Ta thấy miền nghiệm của hệ bất phương trình đã cho là miền tam giác AOB với A(6; 0), O(0; 0) và B(0; 6).
F(6; 0) = 2 . 6 + 3. 0 = 12;
F(0; 0) = 2 . 0 + 3 . 0 = 0;
F(0; 6) = 2 . 0 + 3 . 6 = 18.
Do đó giá trị lớn nhất của F(x; y) = 18 khi x = 0 và y = 6; giá trị nhỏ nhất của F(x; y) = 0 khi x = 0 và y = 0.
Lời giải:
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; -4) và (-4; 0).
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x + y ta được 1 + 1 = 2 > -4.
Suy ra miền nghiệm của bất phương trình x + y ≥ -4 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Vẽ đường thẳng d2: x + y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; 5) và (5; 0).
Chọn điểm I(1; 1) ∉ d2 và thay vào biểu thức x + y ta được 1 + 1 = 2 < 5.
Suy ra miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1).
• Vẽ đường thẳng d3: x - y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; -5) và (5; 0).
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức x + y ta được 1 - 1 = 0 < 5.
Suy ra miền nghiệm của bất phương trình x - y ≤ 5 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1).
• Vẽ đường thẳng d4: x - y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (-4; 0).
Chọn điểm I(1; 1) ∉ d4 và thay vào biểu thức x - y ta được 1 - 1 = 0 > -4.
Suy ra miền nghiệm của bất phương trình x - y ≥ -4 là nửa mặt phẳng bờ d4 chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Miền nghiệm của hệ bất phương trình trên là hình vuông ABCD với A(5; 0), B(0,5; -4,5), C(-4; 0) và D(0,5; 4,5).
F(5; 0) = 4 . 5 - 3 . 0 = 20;
F(0,5; -4,5) = 4 . 0,5 - 3. (-4,5) = 15,5;
F(-4; 0) = 4 . (-4) - 3 . 0 = -16;
F(0,5; 4,5) = 4 . 0,5 - 3 . 4,5 = -11,5.
Vậy giá trị lớn nhất của F(x; y) = 20 khi x = 5 và y = 0 và giá trị nhỏ nhất của biểu thức F(x; y) = -16 khi x = -4 và y = 0.
Lời giải:
Gọi số lít nước A và B cần pha chế lần lượt là x lít và y lít (x ≥ 0; y ≥ 0).
Do 1 lít nước A cần 45 g đường, 1 lít nước và 0,5 g hương liệu nên x lít nước A cần 45x g đường, x lít nước và 0,5x g hương liệu.
Do 1 lít nước B cần 15 g đường, 1 lít nước và 2 g hương liệu nên y lít nước A cần 15y g đường, y lít nước và 2y g hương liệu.
Do có tối đa 12g hương liệu, 9 lít nước và 315 g đường nên 45x + 15y ≤ 315; x + y ≤ 9 và 0,5x + 2y ≤ 12.
Khi đó ta có hệ bất phương trình
Với số điểm thưởng đội chơi nhận được là F(x; y) = 60x + 80y (điểm).
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1)∉ d1 và thay bảo biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Đường thẳng d2: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d2 và thay bảo biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1).
• Vẽ đường thẳng d3: 0,5x + 2y = 12 bằng cách vẽ đường thẳng đi qua hai điểm (0; 6) và (4; 5).
Chọn điểm I(1; 1)∉ d3 và thay bảo biểu thức 0,5x + 2y ta được 0,5 . 1 + 2 . 1 = 2,5 < 12.
Suy ra miền nghiệm của bất phương trình 0,5x + 2y ≤ 12 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1).
• Vẽ đường thẳng d4: x + y = 9 bằng cách vẽ đường thẳng đi qua hai điểm (3; 6) và (4; 5).
Chọn điểm I(1; 1) ∉ d4 và thay bảo biểu thức x + y ta được 1 + 1 = 2 < 9.
Suy ra miền nghiệm của bất phương trình x + y ≤ 9 là nửa mặt phẳng bờ d4 chứa điểm I(1; 1).
• Vẽ đường thẳng d5: 45x + 15y = 315 bằng cách vẽ đường thẳng đi qua hai điểm (5; 6) và (7; 0).
Chọn điểm I(1; 1) ∉ d4 và thay bảo biểu thức 45x + 15y ta được 45 . 1 + 15. 1 = 60 < 315.
Suy ra miền nghiệm của bất phương trình 45x + 15y ≤ 315 là nửa mặt phẳng bờ d5 chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ bất phương trình là miền không bị gạch như hình vẽ dưới đây
Miền nghiệm của hệ là miền ngũ giác ABCDO với A(0; 6), B(4; 5), C(6; 3), D(7; 0) và O(0; 0).
Ta có F(0; 6) = 60 . 0 + 80 . 6 = 480;
F(4; 5) = 60 . 4 + 80 . 5 = 640;
F(6; 3) = 60 . 6 + 80 . 3 = 600;
F(7; 0) = 60 . 7 + 80 . 0 = 420;
F(0; 0) = 0.
Giá trị lớn nhất là F(4; 5) = 640.
Vậy cần pha 4 lít nước loại A và 5 lít nước loại B để số điểm thưởng nhận được là lớn nhất.
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 3: Bất phương trình bậc nhất hai ẩn
Bài 5: Giá trị lượng giác của một góc từ 0° đến 180°
Bài 6: Hệ thức lượng trong tam giác
Lý thuyết Hệ bất phương trình bậc nhất hai ẩn
1. Hệ bất phương trình bậc nhất hai ẩn
- Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
- Cặp số là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.
Ví dụ:
là một hệ bất phương trình hai ẩn gồm 2 bất phương trình và .
không phải là hệ bất phương trình bậc nhất hai ẩn bởi là bất phương trình bậc hai 2 ẩn.
- Cho hệ bất phương trình hai ẩn .
Cặp (x; y) = (10; 2) là nghiệm của bất phương trình x + y > 9 và cũng là nghiệm của bất phương trình x – y < 9. Nên cặp (x; y) = (10; 2) là nghiệm của hệ bất phương trình trên.
2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.
- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:
+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.
+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
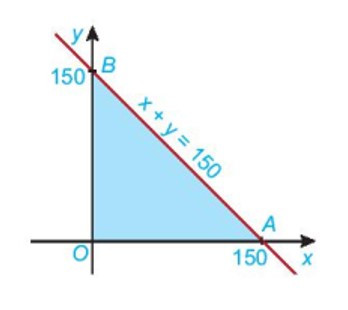
Ví dụ: Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn::
Bước 1: Xác định miền nghiệm D1 của bất phương trình x ≥ 0 và gạch bỏ phần miền còn lại.
- Đường thẳng x = 0 là trục tọa độ Oy.
- Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.
Bước 2: Tương tự, miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.
Bước 3: Miền nghiệm D3 của bất phương trình x + y ≤ 150:
- Vẽ đường thẳng d: x + y = 150.
- Vì 0 + 0 ≤ 150 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 150.
Do đó, miền nghiệm D3 của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Từ đó ta có miền nghiệm tô màu xanh chính là giao miền nghiệm của các bất phương trình trong hệ.
3. Ứng dụng của hệ bất phương trình bậc nhất hai ẩn
Nhận xét: Tổng quát, người ta chứng minh được rằng giá trị lớn nhất (hay nhỏ nhất) của biểu thức , với là tọa độ các điểm thuộc miền đa giác , tức là các điểm nằm bên trong hay nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.
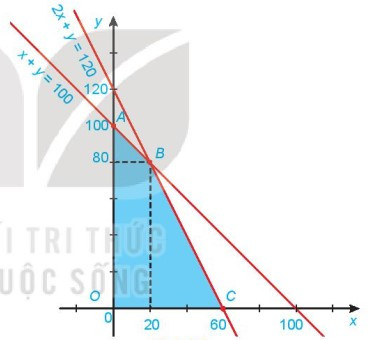
Ví dụ: Cho hệ bất phương trình bậc nhất hai ẩn: và . Tìm giá trị lớn nhất của .
Hướng dẫn giải:
Bước 1: Xác định miền nghiệm của hệ bất phương trình trên.
- Xác định miền nghiệm D1 của bất phương trình x ≥ 0.
- Đường thẳng x = 0 là trục tọa độ Oy.
- Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.
- Tương tự, miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.
- Miền nghiệm D3 của bất phương trình x + y ≤ 100:
+ Vẽ đường thẳng d1: x + y = 100.
+ Vì 0 + 0 ≤ 100 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 100.
Do đó, miền nghiệm D3 của bất phương trình x + y ≤ 100 là nửa mặt phẳng bờ d1 chứa gốc tọa độ O.
- Miền nghiệm D4 của bất phương trình 2x + y ≤ 120:
+ Vẽ đường thẳng d2: 2x + y = 120.
+ Vì 2. 0 + 0 ≤ 120 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình 2x + y ≤ 120.
Do đó, miền nghiệm D4 của bất phương trình 2x + y ≤ 120 là nửa mặt phẳng bờ d2 chứa gốc tọa độ O.
Từ đó ta có miền nghiệm tô màu xanh chính là giao miền nghiệm của các bất phương trình trong hệ.
Miền nghiệm là miền tứ giác OABC với O(0;0), A(0;100), B(20;80) và C(60;0).
Bước 2: Tính giá trị của biểu thức F tại các đỉnh của tứ giác
F(O) = 0; F(A) = 200; F(B) = 230; F(C) = 210.
Bước 3: So sánh các giá trị thu được ở Bước 2, kết luận giá trị lớn nhất của là 230.