Với giải sách bài tập Toán 6 Bài 22: Hình có tâm đối xứng sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 22: Hình có tâm đối xứng
Lời giải:
Những hình có tâm đối xứng: hình bình hành, hình chữ nhật, hình vuông, hình lục giác đều, hình tròn.
+) Tâm đối xứng của hình bình hành ABCD là giao điểm hai đường chéo (tâm O)
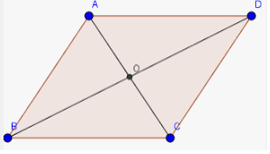
+) Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo
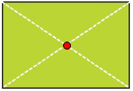
+) Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
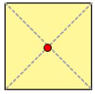
+) Tâm đối xứng của hình lục giác đều là giao điểm của ba đường chéo chính.
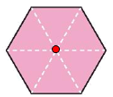
+) Tâm đối xứng của hình tròn là tâm của đường tròn đó.
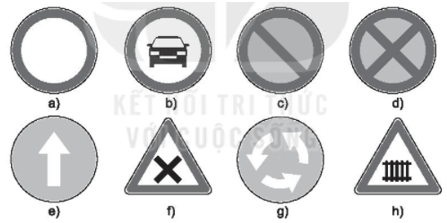
Lời giải:
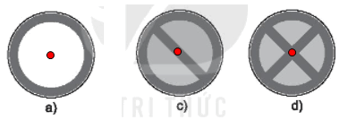
Biển báo có tâm đối xứng là: a), c), d)
+) Tâm đối xứng của các hình đó là:
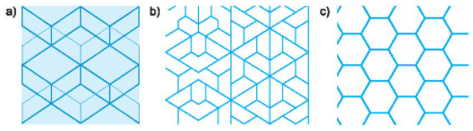
Lời giải:
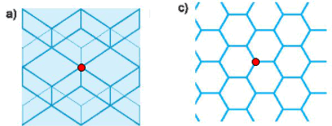
Hình hoa văn có tâm đối xứng là: hình a) và c)
+) Tâm đối xứng của các hình đó là:
Lời giải:
Vì mặt bàn là một hình lục giác đều nên tâm đối xứng là giao điểm của ba đường chéo chính được minh họa như sau:
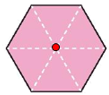
Và hình trên tạo bởi 6 tam giác đều.
Do đó độ dài đường chéo chính gấp 2 lần khoảng cách từ tâm đối xứng đến mỗi đỉnh
Khoảng cách từ tâm đối xứng đến mỗi đỉnh là:
1,2: 2 = 0,6 (m)
Do đó độ dài mỗi cạnh của mặt bàn hình lục giác đều là 0,6 m
Chu vi mặt bàn là:
0,6. 6 = 3,6 (m)
Vậy chu vi mặt bàn là 3,6 m.
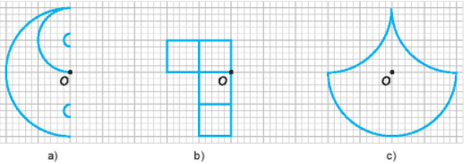
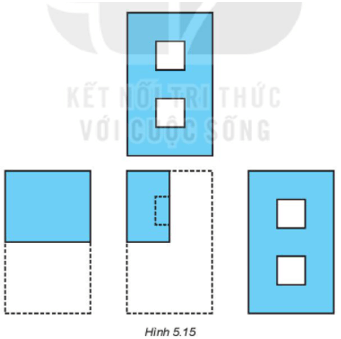
Bài 5.15 trang 87 sách bài tập Toán lớp 6 Tập 1: Trong các hình dưới đây, hình nào có tâm đối xứng?
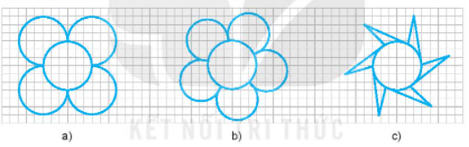
Lời giải:
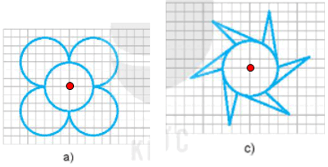
+) Hình có tâm đối xứng là: hình a) và c)
+) Tâm đối xứng của các hình là:
Lời giải:
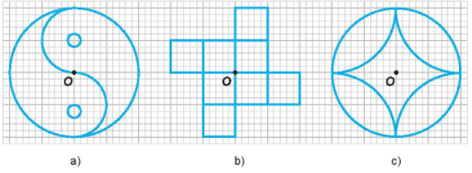
Vẽ thêm hình để các hình có điểm O là tâm đối xứng là:
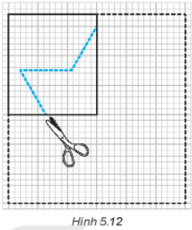
Lời giải:
Khi mở ra, bạn Vuông sẽ nhận được hình như sau:
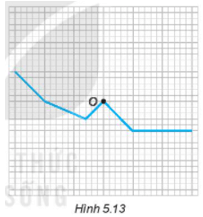
Lời giải:
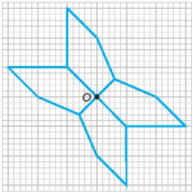
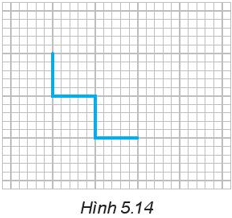
Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng 6 đơn vị để được một hình có tâm đối xứng nhưng không có trục đối xứng;
b) Một đường gấp khúc có độ dài bằng 8 đơn vị để được một hình có tâm đối xứng và có bốn trục đối xứng;
c) Một đường gấp khúc có độ dài ngắn nhất để được một hình có tâm đối xứng;
d) Một đường gấp khúc có độ dài ngắn nhất để được một hình có tâm đối xứng và có trục đối xứng.
Lời giải:
Em vẽ được thành các hình theo yêu câu với tâm đối xứng (chấm đỏ) và trục đối xứng (đường thẳng màu xanh) như sau:
a)
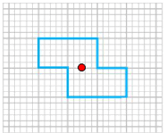
b)
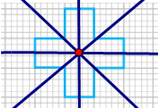
c)
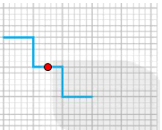
d)
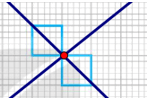
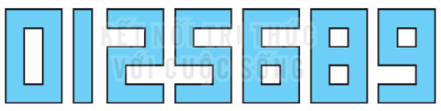
Em có thể ghép được tất cả bao nhiêu “số” như vậy?
Lời giải:
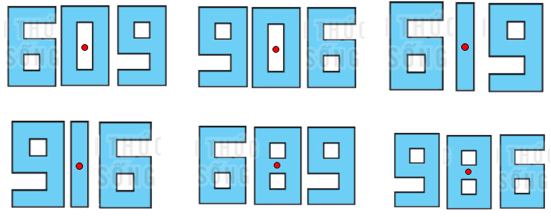
Ta có 6 số có tâm đối xứng là: 609, 906, 619, 916, 689, 986.
+) Tâm đối xứng của các số đó là:
Lời giải:
Cách gấp giấy:
Bước 1: Gấp đôi mảnh giấy theo chiều ngang
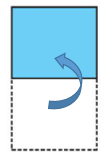
Bước 2: Rồi gấp đôi tiếp theo chiều dọc.
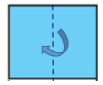
Bước 3: Vẽ rồi cắt theo nét đứt như hình vẽ
Bước 4: Mở miếng giấy ra ta được số 8 như hình vẽ
Lý thuyết Hình có tâm đối xứng
1. Hình có tâm đối xứng trong thực tế
Mỗi hình có mổ điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được “trùng khít” với chính nó ở vị trí ban đầu (trước khi quay).
Những hình như thế được gọi là “hình có tâm đối xứng” và điểm O được gọi là “tâm đối xứng” của hình.
Ví dụ 1. Đoạn thẳng là một hình có tâm đối xứng. Tâm đối xứng của nó là điểm nào?
Lời giải
Cho đoạn thẳng AB có trung điểm là điểm O
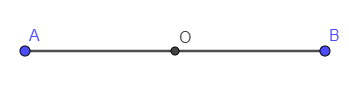
Khi quay đoạn thẳng AB xung quanh điểm O đúng nửa vòng ta thư được hình sau:
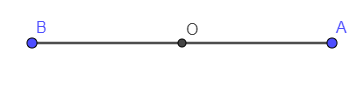
Hình thu được là một hình trùng khít với hình ban đầu.
Do đó đoạn thẳng là một hình có tâm đối xứng và tâm đối xứng của nó là điểm O.
Ví dụ 2. Trong những hình nào dưới đây hình nào có tâm đối xứng? Hãy dự đoán tâm đối xứng và kiểm tra bằng cách quay nửa vòng.
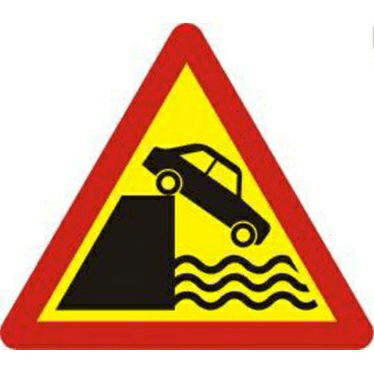
Hình a Hình b Hình c
Lời giải
Hình có tâm đối xứng là hình a
Tâm đối xứng của hình là tâm O của đường tròn.
Khi quay biển báo một nửa vòng quanh tâm O ta được:
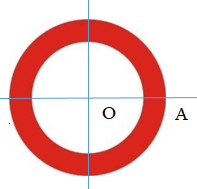
Hình này trùng khít với hình ban đầu.
Do đó hình này có tâm đối xứng và tâm đối xứng là tâm O của đường tròn.
2. Tâm đối xứng của một số hình phẳng
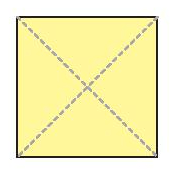
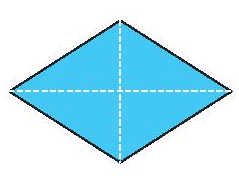
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
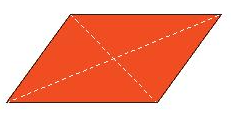
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
