Với tóm tắt lý thuyết Toán lớp 6 Bài 5: Phép nhân và phép chia số tự nhiên sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.

Lý thuyết Toán lớp 6 Bài 5: Phép nhân và phép chia số tự nhiên

Video giải Toán 6 Bài 5: Phép nhân và phép chia số tự nhiên - Kết nối tri thức

A. Lý thuyết Phép nhân và phép chia số tự nhiên

+ Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích. 

Kí hiệu: a.b = c (hoặc a x b = c)

Trong đó: a và b là hai thừa số, c là tích.

+ Chú ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …

Ví dụ 1. Tính:

a) 254.35;                                                   b) 86.72.

Lời giải

a) 

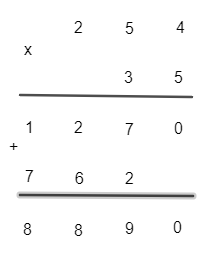
Vậy 254.35 = 8 890.

b) 

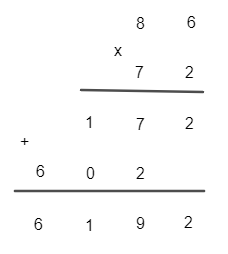
Vậy 86.72 = 6 192.

+ Tính chất của phép nhân:

- Giao hoán: ab = ba.

- Kết hợp: (ab)c = a(bc).

- Phân phối của phép nhân với phép cộng: a(b + c) = ab + ac.

Ví dụ 2. Thực hiện phép tính: 

a) 125.3 542.8;

b) 69.73 + 69.27.

Lời giải

a) 125.3 542.8 

= (125.8).3 542

= 1 000. 3 542 

= 3 542 000.

b) 69.73 + 69.27

= 69.(73 + 27) 

= 69.100

= 6 900.

+ Với hai số tự nhiên a và b đã cho (b khác 0), ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b.q + r, trong đó 0 ≤ r ≤ b.

• Nếu r = 0 thì ta có phép chia hết a:b = q; a là số bị chia, b là số chia, q là thương.
• Nếu r ≠ 0 thì ta có phép chia có dư a:b = q (dư r); a là số bị chia, b là số chia, q là thương, r là số dư.

Ví dụ 3. Thực hiện các phép chia sau:

a) 1 356 : 23;

b) 264 : 12.

Lời giải

a) 

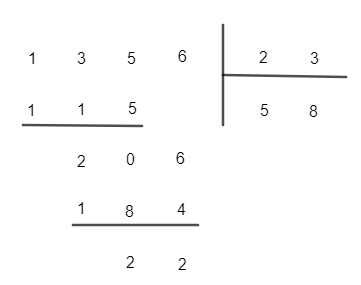
Vậy 1 356 : 23 = 58 (dư 22).

b) 

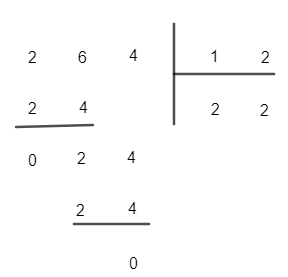
Vậy 264 : 12 = 24 (dư 0)

B. Bài tập

Bài 1. Thực hiện phép tính:

a) 159.32;

b) 4.119.25;

c) 5 902:17;

d) 1938:102.

Lời giải

a) 159.32 = 5 088;

b) 4.119.25 = (4.25).119 = 100.119 = 11 900.

c) 5 092:17 = 299 (dư 9)

d) 1 938:102 = 19.

Bài 2. Một trường Trung học cơ sở có 65 phòng học, mỗi phòng có 12 bộ bàn ghế, mỗi bộ bàn ghế đều có thể xếp cho 4 người ngồi. Trường có thể nhận nhiều nhất bao nhiêu học sinh?

Lời giải

Tổng số bộ bàn ghế của trường Trung học cơ sở là: 65.12 = 780 (bộ)

Vì mỗi bộ bàn ghế đều có thể xếp cho 4 người nên trường có thể nhận nhiều nhất số học sinh là: 780.4 = 3 120 (học sinh).

Vậy trường có thể nhận nhiều nhất 3 120 học sinh.

Bài 3. Một trường học có 1 213 học sinh tham dự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều đủ chỗ người.

Lời giải

Ta có 1 213:5 = 242 (dư 3).

Do đó ban tổ chức cần phải chuẩn bị ít nhất 243 băng ghế như vậy để tất cả học sinh đều đủ chỗ ngồi.

Bài giảng Toán 6 Bài 5: Phép nhân và phép chia số tự nhiên - Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 4:  Phép cộng và phép trừ số tự nhiên

Lý thuyết Bài 5:  Phép nhân và phép chia số tự nhiên

Lý thuyết Bài 6: Lũy thừa với số mũ tự nhiên

Lý thuyết Bài 7: Thứ tự thực hiện các phép tính

Lý thuyết Bài 8: Quan hệ chia hết và tính chất