Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Phép nhân và phép chia số tự nhiên, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Phép nhân và phép chia số tự nhiên. Mời các bạn đón xem:
Bài tập Toán 6 Phép nhân và phép chia số tự nhiên
A. Bài tập Phép nhân và phép chia số tự nhiên
Bài 1. Thực hiện phép tính:
a) 159.32;
b) 4.119.25;
c) 5 902:17;
d) 1938:102.
Lời giải
a) 159.32 = 5 088;
b) 4.119.25 = (4.25).119 = 100.119 = 11 900.
c) 5 092:17 = 299 (dư 9)
d) 1 938:102 = 19.
Bài 2. Một trường Trung học cơ sở có 65 phòng học, mỗi phòng có 12 bộ bàn ghế, mỗi bộ bàn ghế đều có thể xếp cho 4 người ngồi. Trường có thể nhận nhiều nhất bao nhiêu học sinh?
Lời giải
Tổng số bộ bàn ghế của trường Trung học cơ sở là: 65.12 = 780 (bộ)
Vì mỗi bộ bàn ghế đều có thể xếp cho 4 người nên trường có thể nhận nhiều nhất số học sinh là: 780.4 = 3 120 (học sinh).
Vậy trường có thể nhận nhiều nhất 3 120 học sinh.
Bài 3. Một trường học có 1 213 học sinh tham dự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều đủ chỗ người.
Lời giải
Ta có 1 213:5 = 242 (dư 3).
Do đó ban tổ chức cần phải chuẩn bị ít nhất 243 băng ghế như vậy để tất cả học sinh đều đủ chỗ ngồi.
Bài 4. Tính một cách hợp lí:
a) 50 . 347 . 2;
b) 36 . 97 + 97 . 64;
c) 157 . 289 – 289 . 57.
Lời giải:
a) 50 . 347 . 2
= 50 . 2 . 347 (tính chất giao hoán)
= (50 . 2) . 347 (tính chất kết hợp)
= 100 . 347
= 34 700.
b) 36 . 97 + 97 . 64
= 97 . 36 + 97 . 64 (tính chất giao hoán đối với phép nhân)
= 97 . (36 + 64) (tính chất phân phối của phép nhân đối với phép cộng)
= 97 . 100
= 9 700.
c) 157 . 289 – 289 . 57
= 289 . 157 – 289 . 57 (tính chất giao hoán đối với phép nhân)
= 289 . (157 – 57) (tính chất phân phối của phép nhân đối với phép trừ)
= 289 . 100
= 28 900.
Bài 5. Đặt tính rồi tính:
a) 409 . 215;
b) 54 322 : 346;
c) 123 257 : 404.
Lời giải:
a) 409 . 215
Ta có:
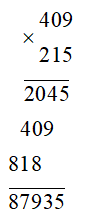
Vậy 409 . 215 = 87 935.
b) 54 322 : 346
Ta có:
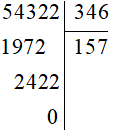
Vậy 54 322 : 346 = 157.
c) 123 257 : 404
Ta có:
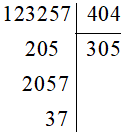
Vậy 123 257 : 404 = 305 (dư 37).
Bài 6. Một trang trại nuôi 70 con bò. Biết trung bình một con bò ăn 30 kg cỏ trong một ngày. Trang trại đó cần bao nhiêu ki-lô-gam cỏ cho đàn bò trong 5 ngày.
Lời giải:
Trong một ngày, 70 con bò ăn hết số ki-lô-gam cỏ là:
30 . 70 = 2 100 (kg)
Trong 5 ngày, 70 con bò ăn hết số ki-lô-gam cỏ là:
2 100 x 5 = 10 500 (kg)
Đáp số: 10 500 kg cỏ.
Câu 7. Với hai số tự nhiên a và b ( b khác 0) Tồn tại số tự nhiên q sao cho a = b.q. Khi đó phát biểu nào sau đây là đúng:
A. a chia hết cho b.
B. b chia hết cho a.
C. a chia cho b dư r.
D. b chia cho a dư r.
Lời giải Nếu tồn tại số tự nhiên q thỏa mãn a = b.q thì a chia hết cho b.
Đáp án: A
Câu 8. Một trường học có 35 lớp học mỗi lớp có 20 bộ bàn ghế. Hỏi trường học đó có bao nhiêu bàn ghế.
A. 70 bộ.
B. 600 bộ.
C. 700 bộ.
D. 500 bộ.
Lời giải Trường học đó có số bộ bàn ghế là: 35. 20 = 700 (bộ).
Đáp án: C
Câu 9. Tính nhẩm: 125. 8 723.8
A. 872 300
B. 8 723 000
C. 87 230 000
D. 8 723.
Lời giải
125. 8 723.8
= (125.8).8 723
= 1000.8 723
= 8 723 000.
Đáp án: B
Câu 10. Giá tiền in một trang giấy A4 là 250 đồng. Hỏi bác Thiệp phải trả bao nhiêu tiền nếu in một tập tài liệu khổ A4 dày 86 trang.
A. 2 150 (đồng).
B. 215 000 (đồng).
C. 21 500 (đồng).
D. 11 500 (đồng).
Lời giải Bác thiệp phải trả số tiền là: 250.86 = 21 500 (đồng).
Đáp án: C
Câu 11. Mẹ Lan mua một túi gạo 15kg gạo loại ngon hết 480 000 đồng. Hỏi một ki – lô – gam gạo giá bao nhiêu tiền?
A. 22 000 đồng.
B. 30 000 đồng.
C. 32 000 đồng.
D. 20 000 đồng.
Lời giải Giá một ki – lô – gam gạo là: 480 000:15 = 32 000 (đồng).
Đáp án: C
Câu 12. Kết quả của phép tính 120.87 + 120.12 + 120
A. 120.
B. 1 200.
C. 12 000.
D. 1 080.
Lời giải
120.87 + 120.12 + 120
= 120.(87 + 12 + 1)
= 120.100
=12 000.
Đáp án: C
Câu 13. Kết quả của phép tính: 47.273 là:
A. 10 011;
B. 12 831;
C. 12 731;
D. 12 031.
Lời giải
Ta có:
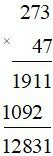
Vậy 47.273 = 12 831.
Đáp án: B
Câu 14: Kết quả của phép tính 159 . 57 – 59 . 57 là:
A. 57
B. 157
C. 570
D. 5 700
Lời giải
Ta có: 159 . 57 – 59 . 57
= (159 – 59) . 57 (tính chất phân phối của phép nhân với phép trừ)
= 100 . 57
= 5 700
Chọn đáp án D.
Câu 15: Số tự nhiên x nào dưới đây thỏa mãn: 2 021 . (x – 2 021) = 2 021.
A. 2 020
B. 2 021
C. 2 022
D. 2 023
Lời giải
Ta có: 2 021 . (x – 2 021) = 2 021
x – 2 021 = 2 021 : 2 021
x – 2 021 = 1
x = 1 + 2 021
x = 2 022
Vậy x = 2 022.
Chọn đáp án C.
Câu 16: Kết quả của phép tính 12 . 100 + 100 . 36 – 100 . 19 là:
A. 29 000
B. 3 800
C. 290
D. 2 900
Lời giải
Ta có:
12 . 100 + 100 . 36 – 100 . 19
= 100 . 12 + 100 . 36 – 100 . 19
= 100 . (12 + 36 – 19)
= 100 . 29 = 2 900
Chọn đáp án D.
Câu 17: Thực hiện phép tính (56 . 35 + 56 . 18) : 53 ta được kết quả là:
A. 12
B. 28
C. 53
D. 56
Lời giải
Ta có: (56 . 35 + 56 . 18) : 53
= [56 . (35 + 18)] : 53
= 56 . 53 : 53
= 56 . (53 : 53)
= 56 . 1
= 56
Chọn đáp án D.
Câu 18: Kết quả của phép tính 0 : a (với a ≠ 0) là:
A. 0
B. 1
C. 2
D. a
Lời giải
Ta có: 0 : a = 0 (với a ≠ 0)
Số 0 chia cho bất kì số tự nhiên nào khác 0 cũng bằng 0.
Chọn đáp án A.
Câu 19: Cho r là số dư trong phép chia a cho b (với b ≠ 0). Khi đó:
A. r = b
B. r > b
C. r > 0
D. 0 ≤ r < b
Lời giải
Trong phép chia, số dư luôn lớn hơn hoặc bằng 0 và nhỏ hơn số chia.
Do đó: r là số dư của phép chia a cho b (với b ≠ 0) thì 0 ≤ r < b.
Chọn đáp án D.
Câu 20: Thực hiện phép chia 1 245 cho 67 được số dư là:
A. 67
B. 39
C. 93
D. 29
Lời giải
Ta đặt tính chia như sau:
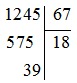
Vậy 1 245 : 67 = 18 (dư 39).
Chọn đáp án B.
Câu 21: Cho phép tính 12 × 5 = 60. Chọn câu sai.
A. 12 là thừa số
B. 5 là thừa số
C. 60 là tích
D. 60 là thương
Lời giải
Trong phép tính 12 × 5 = 60, có 12 và 5 là các thừa số và 60 là tích.
Vậy đáp án A, B, C đúng và D sai.
Chọn đáp án D.
B. Lý thuyết Phép nhân và phép chia số tự nhiên
I. Phép nhân
1. Phép nhân hai số tự nhiên
a x b = c
(thừa số) x (thừa số) = (tích)
Ví dụ: 5 x 2 = 10; 20 x 3 = 60
Quy ước:
+ Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.”
Ví dụ: 5 x 2 = 5 . 2
+ Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số
Ví dụ: a x b = a . b = ab hoặc 4. a . b = 4ab
+ Khi nhân hai số có nhiều chữ số, thông thường đặt tính rồi tính, chú ý khi viết các tích riêng (tích riêng thứ hai lùi sang bên trái một cột so với tích riêng thứ nhất, tích riêng thứ ba lùi sang bên trái hai cột so với tích riêng thứ nhất,…)
Ví dụ: Đặt tính rồi tính: 341 x 157
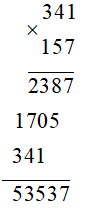
Vậy 341 x 157 = 53 537.
2. Tính chất của phép nhân
Phép nhân các số tự nhiên có các tính chất sau:
+ Giao hoán: a . b = b . a
+ Kết hợp: (a . b) . c = a . (b . c)
+ Nhân với số 1: a . a = 1 . a = a
+ Phân phối đối với phép cộng và phép trừ:
a . (b + c) = a. b + a . c
a . (b – c) = a . b – a . c
Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a. b. c có thể được tính theo một trong hai cách sau:
a . b. c = (a . b) . c hoặc a . b . c = a . (b . c)
Ví dụ: Tính một cách hợp lý:
a) 20 . 36 . 5
b) 34 . 28 + 34 . 72
Lời giải:
a) 20 . 36 . 5
= 20 . 5 . 36 (tính chất giao hoán)
= (20 . 5) . 36 (tính chất kết hợp)
= 100 . 36
= 3 600
b) 34 . 28 + 34 . 72
= 34 . (28 + 72)
= 34 . 100
= 3 400
II. Phép chia
1. Phép chia hết
a : b = q (b#0)
(số bị chia) : (số chia) = (thương)
Ví dụ: 10 : 2 = 5; 30 : 5 = 6
Chú ý:
+ Nếu a : b = q thì q = bq
+ Nếu a : b = q và q 0 thì a : q = b
+ Thông thường, ta đặt tính chia để thực hiện phép chia.
Ví dụ: Đặt tính để tính thương: 139 004 : 236.
Lời giải:
Ta có:
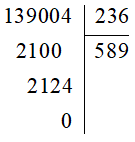
Vậy 139 004 : 236 = 589.
2. Phép chia có dư
Cho hai số tự nhiên a và b với . Khi đó luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó .
Chú ý:
+ Khi r = 0 ta có phép chia hết.
+ Khi r # 0 ta có phép chia có dư. Ta nói: a chia cho b được thương là q và số dư là r.
Kí hiệu: a : b = q (dư r)
Ví dụ: Đặt tính để tính thương và số dư của phép chia:
5 125 : 320.
Lời giải:
Ta có:
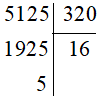
Vậy 5 125 : 320 = 16 (dư 5).