Với giải sách bài tập Toán 6 Bài 5: Phép nhân và phép chia số tự nhiên sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 5: Phép nhân và phép chia số tự nhiên

Bài 1.39 trang 19 sách bài tập Toán lớp 6 Tập 1: Tính nhẩm bằng cách áp dụng tính chất kết hợp của phép nhân:

a) 21. 4

b) 44. 25

c) 125. 56

d) 19. 8

Lời giải:

a) 21. 4 = 21. (2. 2) = (21.2). 2 = 42. 2 = 84

b) 44. 25 = (11. 4). 25 = 11. (4. 25) = 11. 100 = 1 100

c) 125. 56 = 125. (8.7) = (125. 8). 7 = 1 000. 7 = 7 000

d) 19. 8 = 19. (2. 2. 2) = (19. 2). 2. 2 = 38. 2. 2 = 76. 2 = 152

Bài 1.40 trang 19 sách bài tập Toán lớp 6 Tập 1: Tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng:

a) 91. 11       b) 45. 12

Lời giải:

a) 91. 11 = 91. (10 + 1) = 91. 10 + 91. 1 = 910 + 91 = 910 + (90 + 1) = (910 + 90) + 1 

= 1000 + 1 = 1 001

b) 45. 12 = 45. (10 + 2) = 45. 10 + 45. 2 = 450 + 90 = (440 + 10) + 90 = 440 + (90 + 10) = 440 + 100 = 540.

Bài 1.41 trang 19 sách bài tập Toán lớp 6 Tập 1: Tính hợp lí theo mẫu:

25. 19 = 25. (20 – 1) = 25. 20 – 25. 1 = 500 – 25 = 475.

a) 45. 29

b) 47. 98

c) 15. 998.

Lời giải:

a) 45. 29 = 45. (30 – 1) = 45. 30 – 45. 1 = 45. (3. 10) – 45 = (45. 3). 10 – 45

= 135. 10 – 45 = 1 350 – 45 = 1 305.

b) 47. 98 = 47. (100 – 2) = 47. 100 – 47. 2 = 4 700 – 94 = 4 606

c) 15. 998 = 15. (1 000 – 2) = 15. 1 000 – 15. 2 = 15 000 – 30 = 14 970.

Bài 1.42 trang 19 sách bài tập Toán lớp 6 Tập 1: Tính hợp lí:

a) 5. 11. 18 + 9. 31. 10 + 4. 29. 45;

b) 37. 39 + 78. 14 + 13. 85 + 52. 55.

Lời giải:

a) 5. 11. 18 + 9. 31. 10 + 4. 29. 45

= (5. 18). 11 + (9. 10). 31 + (2. 2). 29. 45

= 90. 11 + 90. 31 + (2. 45). (2. 29)

= 90. 11 + 90. 31 + 90. 58

= 90. (11 + 31 + 58)

= 90. 100

= 9 000

b) 37. 39 + 78. 14 + 13. 85 + 52. 55

= 37. 39 + (39. 2). 14 + 13. (5. 17) + (13. 4). (5. 11)

= 37. 39 + 39. (2. 14) + (13. 5). 17 + (13. 5). (4. 11)

= 39. 37 + 39. 28 + 65. 17 + 65. 44

= (39. 37 + 39. 28) + (65. 17 + 65. 44)

= 39. (37 + 28) + 65. (17 + 44)

= 39. 65 + 65. 61

= 65. 39 + 65. 61

= 65. (39 + 61)

= 65. 100

= 6 500

Bài 1.43 trang 19 sách bài tập Toán lớp 6 Tập 1: Dưới đây là ảnh chụp bài kiểm tra của bạn Lê, cô giáo phê Sai. Hãy giải thích những lỗi sai của bạn Lê.

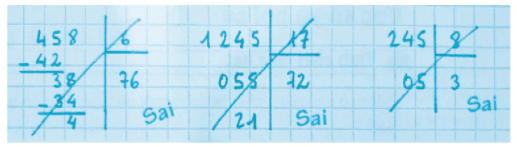
Lời giải:

+) Phép tính thứ nhất: 

Ở tích riêng thứ hai phải là 6. 6 = 36 chứ không phải 6. 6 = 34 như bài Lê làm

+) Phép tính thứ hai:

Trong phép tính thứ hai số dư 21 lớn hơn số chia 17 nên không đúng vì 55: 17 = 3 (dư 4)

+) Phép tính thứ ba: 

Còn phải chia 5 cho 8 (được 0 dư 5). Như thế thương là 30, không phải là 3 như bài làm.

Bài 1.44 trang 20 sách bài tập Toán lớp 6 Tập 1: Một hình chữ nhật có chiều dài bằng 16cm; diện tích bằng a cm². Tính chiều rộng của hình chữ nhật này (là một số tự nhiên) nếu biết a là một số tự nhiên từ 220 đến 228.

Lời giải:

Giả sử chiều rộng của hình chữ nhật là b (cm, b > 0, b ∈ N).

Diện tích của hình chữ nhật là: a = 16. b (cm²)

Mà theo bài toán a là một số tự nhiên từ 220 đến 228 nên 220 ≤ a ≤ 228  hay 

220 ≤ 16b ≤ 228. Do đó: 220 : 16 ≤ b ≤ 228

Phép chia 220: 16 = 13 (dư 12)

Phép chia 228: 16 = 14 (dư 4)

Vì b ∈ Nnên suy ra b = 14 cm.

Vậy chiều rộng của hình chữ nhật là 14cm.

Bài 1.45 trang 20 sách bài tập Toán lớp 6 Tập 1: Giả sử máy tính cầm tay của bạn bị hỏng các phím . Với các phím còn lại, bạn cần bấm thế nào để màn hình hiện phép nhân có kết quả 3 232?

Lời giải:

Ta có: 3 232 = 3 200 + 32 = 32. 100 + 32 = 32. 100 + 32. 1 = 32. (100 + 1) = 32. 101 = (4. 8). 101 = 4. (8. 101) = 4. 808.

Vì vậy muốn màn hình hiện kết quả là 3 232 ta bấm lần lượt các phím:

Bài 1.46 trang 20 sách bài tập Toán lớp 6 Tập 1:a) Khẩu phần ăn nhẹ bữa chiều của các bé mẫu giáo là một cái bánh. Nếu trường có 537 cháu thì phải mở bao nhiêu hộp bánh, biết rằng mỗi hộp có 16 chiếc bánh;

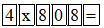
b) Một quyển vở ô li 200 trang có giá 17 nghìn đồng. Với 300 nghìn đồng bạn có thể mua được nhiều nhất là bao nhiêu quyển vở loại này?

Lời giải:

a) Ta có: 537: 16 = 33 (dư 9). Do vậy phải mở thêm 1 hộp bánh cho 9 bé ăn

Vậy nếu trường có 537 cháu thì phải mở: 33 + 1 = 34 hộp bánh.

b) Ta có: 300: 17 = 17 (dư 11).

Vậy với 300 nghìn đồng bạn chỉ có thể mua được nhiều nhất 17 quyển vở (vì dư 11 trong phép chia trên, tức là còn thừa 11 nghìn < 17 nghìn nên không thể mua được thêm quyển vở 200 trang nữa).

Bài 1.47 trang 20 sách bài tập Toán lớp 6 Tập 1: Không đặt tính, hãy so sánh:

a) m = 19. 90 và n = 31. 60

b) p = 2 011. 2 019 và q = 2 015. 2 015.

Lời giải:

a)

+) m = 19. 90 = 19. (3. 30) = (19. 3). 30

+) n = 31. 60 = 31. (3. 20) = (20. 3). 31

Vì 19 < 20; 30 < 31 nên (19. 3). 30 < (20. 3). 31 hay m < n.

Vậy m < n.

b) p = 2 011. 2 019 = 2 011. (2 015 + 4) = 2 011. 2 015 + 2 011. 4 

    q = 2 015. 2 015 = (2 011 + 4). 2 015 = 2 011. 2 015 + 4. 2015

       = 2 011. 2 015 + 2 015. 4

Vì 2 011 < 2 015 nên 2 011. 4 < 2 015. 4 

hay 2 011. 2 015 + 2 011. 4 < 2 011. 2 015 + 2 015. 4

Do đó p < q

Vậy p < q.

Bài 1.48 trang 20 sách bài tập Toán lớp 6 Tập 1: Áp dụng các tính chất của phép cộng và phép nhân, tính nhanh:

a) (1 989. 1 990 + 3 978): (1 992. 1 991 – 3 984);

b) (637. 527 – 189): (526. 637 + 448)

Lời giải:

a) (1 989. 1 990 + 3 978): (1 992. 1 991 – 3 984)

+) 1 989. 1 990 + 3 978 = 1 989. 1 990 + 1 989. 2 = 1 989. (1 990 + 2) = 1 989. 1 992

+) 1 992. 1 991 – 3 984 = 1 992. 1 991 – 1 992. 2 = 1 992. (1 991 – 2) = 1 992. 1 989

Do đó: 

(1 989. 1 990 + 3 978): (1 992. 1 991 – 3 984)

= (1 989. 1 992): (1 992. 1 989)

= (1 989: 1 989). (1 992: 1 992)

= 1. 1  

= 1

b) (637. 527 – 189): (526. 637 + 448)

+) 637. 527 – 189 = 637. (526 + 1) – 189 = 637. 526 + 637. 1 – 189 

= 637. 526 + (637 – 189) = 637. 526 + 448

Do đó: (637. 527 – 189): (526. 637 + 448) = (637. 526 + 448): (637. 526 + 448) = 1.

Bài 1.49 trang 20 sách bài tập Toán lớp 6 Tập 1: Kết quả của mỗi phép nhân sau là một trong bốn phương án (A), (B), (C), (D) cho trong bảng. Hãy tìm phương án đúng mà không đặt tính.

Lời giải:

a) Có 9 < 10 nên 753. 9 < 753. 10 = 7 530 nên (B) và (D) sai vì 7 777 > 7 530 và 

16 777 > 7 530

Mặt khác ta có 753 > 700 nên 753. 9 > 700. 9 = 6 300 nên (C) sai vì 6 256 < 6 300.

Vậy phương án (A) là đúng.

b) Có 456 < 500, 398 < 400 nên 456. 398 < 500. 400 = 200 000 nên (A) và (C) sai vì 

381 488 > 200 000 và 358 948 > 200 000.

Lại có: 456 > 400, 398 > 300 nên 456. 398 > 400. 300 = 120 000 nên (B) sai vì 

39 888 < 120 000.

Vậy phương án (D) là đúng.

Bài 1.50 trang 20 sách bài tập Toán lớp 6 Tập 1: Không đặt tính, hãy so sánh:

a) a = 53. 571 và b = 57. 531

b) a = 25. 26 261 và b = 26. 25 251

Lời giải:

a) 

a = 53. 571 = 53. (531 + 40) = 53. 531 + 53. 40 = 53. 531 + 53. (10.4)

= 53. 531 + (53. 10). 4 = 53. 531 + 530. 4

b = 57. 531 = (53 + 4). 531 = 531. (53 + 4) = 531. 53 + 531. 4 

Vì 530 < 531 nên 530. 4 < 531. 4 do đó 53. 531 + 530. 4 < 531. 53 + 531. 4 hay a < b.

Vậy a < b.

b)

a = 25. 26 261 = 25. (26 260 + 1) = 25. 26 260 + 25. 1 = 25. (10. 2 626) + 25

= (25. 10). 2 626 + 25 

= 25. 10. (26. 101) + 25 = 10. 25. 26. 101 + 25;

b = 26. 25 251 = 26. (25 250 + 1) = 26. 25 250 + 26. 1 = 26. (10. 2 525) + 26

= 26. 10. 2 525 + 26 = 26. 10. 25. 101 + 26 = 10. 25. 26. 101 + 26;

Vì 25 < 26 nên 10. 25. 26. 101 + 25 < 10. 25. 26. 101 + 26 hay a < b.

Vậy a < b.

Lý thuyết Phép nhân và phép chia số tự nhiên

+ Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích. 

Kí hiệu: a.b = c (hoặc a x b = c)

Trong đó: a và b là hai thừa số, c là tích.

+ Chú ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …

Ví dụ 1. Tính:

a) 254.35;                                                   b) 86.72.

Lời giải

a) 

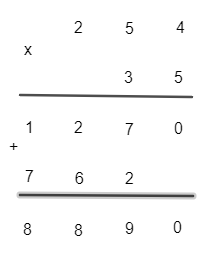
Vậy 254.35 = 8 890.

b) 

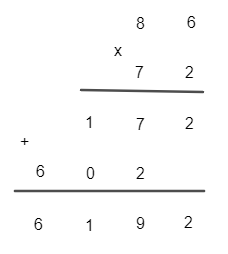
Vậy 86.72 = 6 192.

+ Tính chất của phép nhân:

- Giao hoán: ab = ba.

- Kết hợp: (ab)c = a(bc).

- Phân phối của phép nhân với phép cộng: a(b + c) = ab + ac.

Ví dụ 2. Thực hiện phép tính: 

a) 125.3 542.8;

b) 69.73 + 69.27.

Lời giải

a) 125.3 542.8 

= (125.8).3 542

= 1 000. 3 542 

= 3 542 000.

b) 69.73 + 69.27

= 69.(73 + 27) 

= 69.100

= 6 900.

+ Với hai số tự nhiên a và b đã cho (b khác 0), ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b.q + r, trong đó 0 ≤ r ≤ b.

• Nếu r = 0 thì ta có phép chia hết a:b = q; a là số bị chia, b là số chia, q là thương.
• Nếu r ≠ 0 thì ta có phép chia có dư a:b = q (dư r); a là số bị chia, b là số chia, q là thương, r là số dư.

Ví dụ 3. Thực hiện các phép chia sau:

a) 1 356 : 23;

b) 264 : 12.

Lời giải

a) 

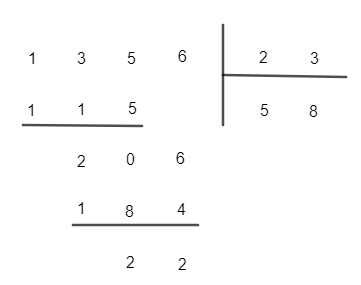
Vậy 1 356 : 23 = 58 (dư 22).

b) 

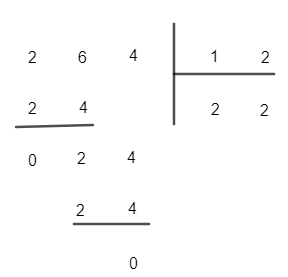
Vậy 264 : 12 = 24 (dư 0)