Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024

vietjack13 Ngày: 16-04-2024 Lớp 8

Mua tài liệu 4.7 K

Tailieumoi.vn xin giới thiệu bộ đề thi học kì 2 môn Toán lớp 8 sách Cánh diều năm 2023 – 2024. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 2 Toán 8. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 8 Cánh diều bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024

Đề thi học kì 2 Toán 8 Cánh diều có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Cánh diều

Năm học 2023 - 2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Mỗi câu lạc bộ tại trường Trung học Kim Đồng có 15 học sinh. Số lượng học sinh nam và học sinh nữ của mỗi câu lạc bộ được biểu diễn trong bảng số liệu sau đây:

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Biết trong biểu đồ, dữ liệu thống kê của một câu lạc bộ chưa chính xác, đó là

A. Cầu lông.

B. Bóng bàn.

C. Cờ vua.

D. Không có dữ liệu chưa chính xác trong biểu đồ.

Câu 2. Lớp 8C có 38 bạn, trong đó có 17 nữ. Cô giáo chọn ngẫu nhiên một bạn làm sao đỏ. Xác suất cô chọn trúng một bạn nam là

A. $\frac{17}{38}$ .

B. $\frac{13}{38}$ .

C. $\frac{11}{38}$ .

D. $\frac{21}{38}$ .

Câu 3. Phương trình nào sau đây là phương trình bậc nhất một ẩn?

A. 0x + 3 = 0.

B. x² - 2 = 0.

C. $\frac{1}{2} x - 3 = 0$ .

D. $\frac{5}{x} + 1 = 0$ .

Câu 4. Cho hình vẽ bên, biết DE // AC.

Tỉ số nào sau đây là đúng?

A. $\frac{B D}{A D} = \frac{B E}{B C}$ .

B. $\frac{B D}{A D} = \frac{B E}{E C}$ .

C. $\frac{D E}{A C} = \frac{B C}{B E}$ .

D. $\frac{A D}{A B} = \frac{B C}{E C}$ .

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Câu 5. Cho các mệnh đề sau:

(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.

(II) Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.

Hãy chọn đáp án đúng:

A. Cả (I) và (II) đều đúng.

B. Chỉ có (II) đúng.

C. Chỉ có (I) đúng.

D. Cả (I) và (II) đều sai.

Câu 6. Cho ∆RSK và ∆RSK có $\frac{R S}{P Q} = \frac{R K}{P M} = \frac{S K}{Q M}$ , khi đó ta có

A. ∆RSK ᔕ ∆MPQ.

B. ∆RSK ᔕ ∆PQM.

C. ∆RSK ᔕ ∆QPM.

D. ∆RSK ᔕ ∆QMP.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm) Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 theo mẫu sau:

Năm	Tháng 10	Tháng 11	Tháng 12
Số gạo bán được (kg)

b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Bài 2. (1,5 điểm) Hiệu hai số là 12. Nếu chia số bé cho 7 và lớn cho 5 thì thương thứ nhất lớn hơn thương thứ hai là 4 đơn vị. Tìm hai số đó.

Bài 3. (1,0 điểm) Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Nhà giáo Việt Nam 20/11, cô giáo đã chọn ra 10 học sinh gồm 4 học sinh nữ nữ là Hoa; Mai; Linh; My; 6 học sinh nam là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm 10 học sinh tập múa trên.

a) Tìm số phần tử của tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra.

Bài 4. (3,0 điểm)

1. Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm A đến trường (tại điểm B phải leo lên và xuống một con dốc với đỉnh dốc tại điểm C (như hình vẽ).

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Điểm H là một điểm thuộc đoạn thẳng AB sao cho CH đường là phân giác $\hat{A C B}$ , AH = 0,32 km và BH = 0,4 km. Biết bạn Hải đi xe đạp đến C lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h?

2. Cho tam giác ABC có ba góc nhọn (AB < AC) có ba đường cao AE, BD, CF cắt nhau tại H.

a) Chứng minh: ∆ABD đồng dạng với ∆ACF.

b) Chứng minh: ∆ADF đồng dạng với ∆ABC.

c) Chứng minh: BH.BD + CH.CF = BC²và $\frac{H E}{A E} + \frac{H D}{B D} + \frac{H F}{C F}$ = 1.

Bài 5. (0,5 điểm) Tìm nghiệm nguyên của phương trình 2xy - x + y = 3.

−−−−−HẾT−−−−−

ĐÁP ÁN & HƯỚNG DẪN

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5	6
Đáp án	B	D	C	B	C	A

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm)

a) Ta có bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 như sau:

Năm	Tháng 10	Tháng 11	Tháng 12
Số gạo bán được (kg)	200	250	225

b) Biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh là:

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Bài 2. (1,5 điểm)

Gọi số bé là x ( $x \in ℕ *$ ).

Số lớn là x + 12.

Chia số bé cho 7 ta được thương là $\frac{x}{7}$ .

Chia số lớn cho 5 ta được thương là $\frac{x + 12}{5}$ .

Vì thương thứ nhất lớn hơn thương thứ hai 4 đơn vị nên ta có phương trình:

$\frac{x + 12}{5} - \frac{x}{7} = 4$

7(x + 12) - 5x = 140

7x + 84 - 5x = 140

2x = 56

x = 28

Vậy số bé là 28; số lớn là: 28 + 12 = 40.

Bài 3. (1,0 điểm)

a) Tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra là :

M = {Hoa; Mai; Linh; My; Cường; Hường; Mỹ; Kiên; Phúc; Hoàng}.

Số phần tử của tập hợp M là 10.

b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nam” đó là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng.

Vì thế xác suất của biến cố đó là $\frac{6}{10} = \frac{3}{5}$ .

Bài 4. (3,0 điểm)

1. 10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Thời gian để bạn Hải đi từ A đến C là: 6 giờ 30 phút - 6 giờ = 30 phút = 0,5 giờ.

Quãng đường mà bạn Hải đi từ A đến C trong 0,5 giờ với tốc độ trung bình lên dốc 4 km/h là: AC = $S_{A \to C}$ = 4.0,5 = 2 (km).

Xét ∆ACB có CH là đường phân giác của $\hat{A C B}$ , nên ta có:

$\frac{H A}{H B} = \frac{C A}{C B}$ hay $\frac{0,32}{0,4} = \frac{2}{C B}$ . Suy ra $C B = \frac{0,4 \cdot 2}{0,32} = 2,5$ (km).

Thời gian để bạn Hải đi hết quãng đường2,5 km với tốc độ trung bình xuống dốc 10 km/h là: $\frac{2,5}{10} = 0,25$ (giờ).

Như vậy, tổng thời gian bạn Hải đi từ A đến trường B là:

0,5 + 0,25 = 0,75 (giờ) = 45 (phút).

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Vì H là giao của ba đường cao AE, BD, CF nên H là trực tâm của tam giác ABC.

a) Xét ∆ABD và ∆ACF có:

$\hat{B A D} = \hat{C A F}$ ; $\hat{A D B} = \hat{A F C} (= 90 °)$

Do đó $Δ A B D ∽ Δ A C F (g.g)$ .

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

• Mặt khác, ta có:

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Bài 5. (0,5 điểm)

Ta có 2xy - x + y = 3

4xy - 2x + 2y = 6

4xy - 2x + 2y - 1 = 6 - 1

2x(2y - 1) + (2y - 1) = 6 - 1

(2y - 1)(2y - 1) = 5

Ta có x và y là các số nguyên nên 2x + 1 và 2y - 1 là các số nguyên và là ước của 5.

Từ đó, ta có bảng sau:

10 Đề thi Học kì 2 Toán 8 Cánh diều (có đáp án + ma trận)

Vậy phương trình có nghiệm là: $(x, y) \in \{(3, 0); (- 1, - 2); (2, 1); (- 3, 0)\}$ .

Đề thi học kì 2 Toán 8 Cánh diều có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Cánh diều

Năm học 2023 - 2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề số 2)

I. Trắc nghiệm

Câu 1 : Trong các phương trình sau, phương trình bậc nhất một ẩn là

A.
$2 x + 1 = 0$ .
B.
$\frac{1}{x} + 2 = 0$ .
C.
$x^{2} + 2 x + 1 = 0$ .
D.
$x^{2} - 1 = 0$ .

Câu 2 : Phương trình nào sau đây nhận $m = 2$ là nghiệm?

A.
$m - 2 = 0$ .
B.
$2 m = 0$ .
C.
$m + 2 = 0$ .
D.
$- m + 3 = 0$ .

Câu 3 : Phương trình $x + 5 = x + 5$ có

A.
vô số nghiệm.
B.
vô nghiệm.
C.
1 nghiệm.
D.
2 nghiệm.

Câu 4 : Năm nay tuổi cha 39 tuổi và gấp 3 lần tuổi con năm ngoái. Vậy năm nay tuổi con là

A.
12 tuổi.
B.
13 tuổi.
C.
14 tuổi.
D.
15 tuổi.

Câu 5 : Tiền lương cơ bản của An mỗi tháng là x (triệu đồng). Tiền phụ cấp mỗi tháng là 2 000 000 (đồng). Biểu thức biểu thị tiền lương mỗi tháng của An (bằng tổng tiền lương cơ bản và tiền phụ cấp; đơn vị là triệu đồng) là:

A.
$x + 2000000$ .
B.
$x + 200$ .
C.
$x - 2$ .
D.
$x + 2$ .

Câu 6 : Cho $Δ A B C ∽ Δ D E F$ biết AB = 4 cm; AC = 6 cm; BC = 10 cm và DE = 2 cm khi đó tỉ số đồng dạng bằng

A.
3.
B.
2.
C.
5.
D.
4.

Câu 7 : Hãy chỉ ra cặp tam giác đồng dạng trong các tam giác sau

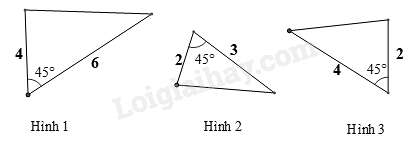
Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024 (ảnh 1)

A.
Hình 1 và Hình 2.
B.
Hình 2 và Hình 3.
C.
Hình 1 và Hình 3.
D.
Đáp án A và C đều đúng.

Câu 8 : Cho $Δ G H I ∽ Δ F E I$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:

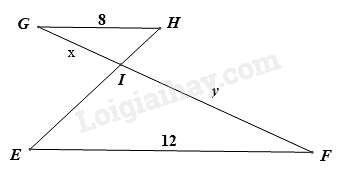
Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024 (ảnh 2)

A.
$4$ .
B.
$\frac{2}{3}$ .
C.
$\frac{3}{2}$ .
D.
$6$ .

Câu 9 : Cho hình vẽ

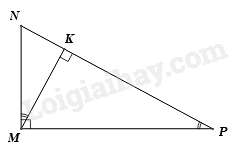
Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024 (ảnh 3)

Khi đó các khẳng định sau

(1) $Δ M K N ∽ Δ P K M (g .g)$ .

(2) $Δ M K P ∽ Δ M N P (g .g)$ .

Hãy chọn đáp án đúng:

A.
Chỉ có (1) đúng.
B.
Chỉ có (2) đúng.
C.
(1) và (2) đều đúng.
D.
(1) và (2) đều sai.

Câu 10 : Cho hình vẽ sau, biết $\hat{B} = \hat{D}, B C = 50 c m, A B = 40 c m, D E = 30 c m$ . Độ dài đoạn thẳng CD là:

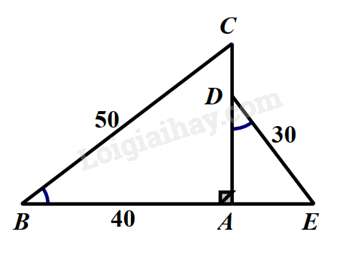
Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024 (ảnh 4)

A.
30cm.
B.
24cm.
C.
50cm.
D.
18cm.

Câu 11 : Trong các hình đã học cặp hình nào sau đây luôn đồng dạng?

A.
Hình bình hành.
B.
Hình chữ nhật.
C.
Hình thoi.
D.
Hình vuông.

Câu 12 : Trong hình dưới đây, hình b là hình a sau khi phóng to với kích thước k = 2. Nếu kích thước của hình a là 3 x 4 thì kích thước của hình b là:

Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024 (ảnh 5)

A.
1,5 x 2.
B.
6 x 8.
C.
6 x 9.
D.
9 x 16.

II. Tự luận

Câu 1 : Giải các phương trình sau:

a) $2 x - 4 = 3 x + 1$

b) $7 (5 - x) = 11 - 5 x$

c) $\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}$

d) $\frac{2 (x + 1)}{3} = \frac{1 + 3 x}{4} + \frac{1}{2}$

Câu 2 : Giải bài toán bằng cách lập phương trình

Có hai loại dung dịch muối I và II. Người ta hòa 200 gam dung dịch muối I với 300 gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.

Câu 3 : Cho $Δ A B C$ vuông tại A có $A B = 6 c m$ và $A C = 8 c m$ . Đường phân giác của góc ABC cắt AC tại D. Từ C kẻ $C E ⊥ B D$ kẻ E.

a) Tính độ dài BC và tỉ số $\frac{A D}{D C}$ .

b) Chứng minh $Δ A B D ∽ Δ E B C$ . Từ đó suy ra $B D . E C = A D . B C$ .

c) Chứng minh $\frac{C D}{B C} = \frac{C E}{B E}$ .

d) Gọi EH là đường cao của $Δ E B C$ . Chứng minh $C H . H B = E D . E B$ .

Câu 4 : Chu vi của một mảnh vườn hình chữ nhật là 42 m. Biết chiều rộng ngắn hơn chiều dài 3 m. Tìm chiều dài của mảnh vườn.

Câu 5 : Cho $a_{1}; a_{2}; . . .; a_{2024}$ là 2024 số thực thỏa mãn $a_{k} = \frac{2 k + 1}{{(k^{2} + k)}^{2}}$ với $k \in {1; 2; . . .; 2024}$ .

Tính tổng $S_{2024} = a_{1} + a_{2} + a_{3} + . . . + a_{2024}$ .

ĐÁP ÁN

I. Trắc nghiệm

Câu 1 :

Phương trình bậc nhất một ẩn là phương trình $2 x + 1 = 0$ .

Đáp án A.

Câu 2 :

Ta có: 2 – 2 = 0 nên phương trình m – 2 nhận m = 2 là nghiệm.

Đáp án A.

Câu 3 :

$\begin{array}{l} x + 5 = x + 5 \\ x - x = 5 - 5 \end{array}$

$0 = 0$ (luôn đúng)

Vậy phương trình $x + 5 = x + 5$ có vô số nghiệm.

Đáp án A.

Câu 4 :

Gọi tuổi của con hiện tại là x $(x > 1, x \in N *)$

Vì năm nay cha 39 tuổi và gấp 3 lần tuổi con năm ngoái nên ta có phương trình:

$\begin{array}{l} 3 (x - 1) = 39 \\ x - 1 = 13 \\ x = 14 (T M) \end{array}$

Vậy năm nay con 14 tuổi.

Đáp án C.

Câu 5 :

Vì tiền lương mỗi tháng của An bằng tổng tiền lương cơ bản và tiền phụ cấp nên ta có biểu thức:

$x + 2$ (triệu đồng)

Đáp án D.

Câu 6 :

Vì $Δ A B C ∽ Δ D E F$ nên tỉ số đồng dạng là: $k = \frac{A B}{D E} = \frac{A C}{D F} = \frac{B C}{E F}$ hay $k = \frac{A B}{D E} = \frac{4}{2} = 2$ .

Đáp án B.

Câu 7 :

Xét hình 1 và hình 2 có một góc $45^{0}$ , tỉ số hai cạnh kề góc dó là $\frac{4}{6} = \frac{2}{3}$ nên hình 1 và hình 2 là hai tam giác đồng dạng.

Xét hình 1 và hình 2 có một góc $45^{0}$ , tỉ số hai cạnh kề góc dó là $\frac{4}{6} = \frac{2}{3} \neq \frac{2}{4}$ nên hình 1 và hình 3 không là hai tam giác đồng dạng.

Từ đó suy ra hình 2 và hình 3 cũng không đồng dạng.

Vậy A đúng.

Đáp án A.

Câu 8 :

Vì $Δ G H I ∽ Δ F E I$ nên $\frac{x}{y} = \frac{I F}{G I} = \frac{E F}{G H} = \frac{12}{8} = \frac{3}{2}$ .

Đáp án C.

Câu 9 :

$Δ M K N$ và $Δ P K M$ có $\hat{N}$ chung, $\hat{M} = \hat{K} = 90^{0}$ nên $Δ M K N ∽ Δ P K M$ (g.g) suy ra khẳng định (1) đúng.

Tương tự $Δ M K P ∽ Δ N M P$ (g.g). Khẳng định (2) không đúng vì các đỉnh của hai tam giác đồng dạng chưa được viết chính xác.

Vậy chỉ có khẳng định (1) đúng.

Đáp án A.

Câu 10 :

Xét $Δ A B C$ và $Δ A D E$ có:

$\hat{B} = \hat{D}$

$\hat{C A B} = \hat{E A D} (= 90^{0})$

Suy ra $Δ A B C ∽ Δ A D E$ (g.g) suy ra $\frac{A B}{B C} = \frac{A D}{D E}$ hay $\frac{40}{50} = \frac{A D}{30}$ suy ra $A D = 30. \frac{40}{50} = 24$ (cm).

Đáp án B.

Câu 11 :

Trong các hình trên chỉ có hình vuông là hình có các cạnh bằng nhau, các góc bằng nhau nên luôn đồng dạng.

Đáp án D.

Câu 12 :

Vì hình b là hình a sau khi phóng to với kích thước k = 2 nên cạnh của hình b gấp 2 lần cạnh của hình a.

Ta có: 3.2 = 6; 4.2 = 8

$\Rightarrow$ Kích thước hình b là 6 x 8.

Đáp án B.

II. Tự luận

Câu 1 :

a) $2 x - 4 = 3 x + 1$

$\begin{array}{l} 2 x - 3 x = 1 + 4 \\ - x = 5 \\ x = - 5 \end{array}$

Vậy $x = - 5$ .

b) $7 (5 - x) = 11 - 5 x$

$\begin{array}{l} 35 - 7 x = 11 - 5 x \\ - 7 x + 5 x = 11 - 35 \\ - 2 x = - 24 \\ x = 12 \end{array}$

Vậy $x = 12$ .

c) $\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}$

$\begin{array}{l} \frac{10}{12} + \frac{3 x}{12} = \frac{24}{12} - \frac{4 x}{12} \\ 10 + 3 x = 24 - 4 x \\ 3 x + 4 x = 24 - 10 \\ 7 x = 14 \\ x = 2 \end{array}$

Vậy $x = 2$ .

d) $\frac{2 (x + 1)}{3} = \frac{1 + 3 x}{5} + \frac{1}{2}$

$\begin{array}{l} \frac{10.2 (x + 1)}{30} = \frac{6 (1 + 3 x)}{30} + \frac{15}{30} \\ 20 (x + 1) = 6 (1 + 3 x) + 15 \\ 20 x + 20 = 6 + 18 x + 15 \\ 20 x - 18 x = 6 + 15 - 20 \\ 2 x = 1 \\ x = \frac{1}{2} \end{array}$

Vậy $x = \frac{1}{2}$ .

Câu 2 :

Gọi nồng độ muối trong dung dịch I là $x (%) (x > 0)$ .

Khi đó khối lượng muối có trong dung dịch I là:

$200. x % = 200 \frac{x}{100} = 2 x$ (g).

Do nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20% nên nồng độ muối trong dung dịch II là $x - 20 (%)$

Khi đó khối lượng muối có trong dung dịch II là:

$300. (x - 20) % = 300. \frac{x - 20}{100} = 3 (x - 20)$ (g).

Khối lượng muối trong dung dịch sau khi trộn hai dung dịch là:

$2 x + 3 (x - 20)$ (g).

Khối lượng dung dịch muối sau khi trộn hai dung dịch là: $200 + 300 = 500$ (g).

Do sau khi trộn hai dung dịch I và II thì được một dung dịch có nồng độ muối là 33% nên ta có phương trình: $\frac{2 x + 3 (x - 20)}{500} .100 % = 33 %$ hay $2 x + 3 (x - 20) = 165$

Giải phương trình ta được $x = 45$ (thỏa mãn).

Suy ra nồng độ muối trong dung dịch II là: $40 - 20 = 25 (%)$

Vậy nồng độ muối của dung dịch I và II lần lượt là 45% và 25%.

Câu 3 :

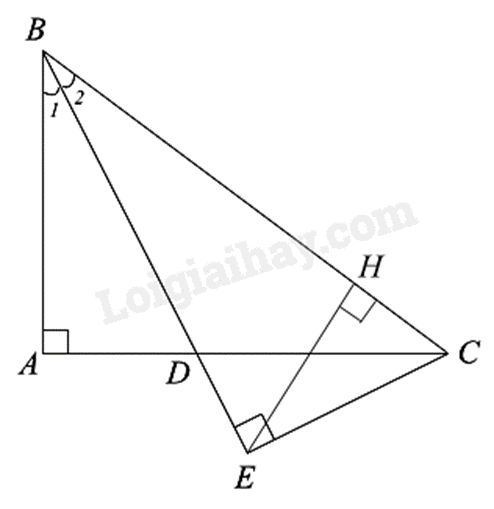
Bộ 10 đề thi học kì 2 Toán 8 Cánh diều có đáp án năm 2024 (ảnh 6)

a) Áp dụng định lí Pythagore vào $Δ A B C$ vuông tại A, ta có:

$B C^{2} = A B^{2} + A C^{2} = 6^{2} + 8^{2} = 100$

Suy ra $B C = \sqrt{100} = 10$ (cm).

Vì BD là tia phân giác của góc ABC nên ta có:

$\frac{D A}{D C} = \frac{B A}{B C} = \frac{6}{10} = \frac{3}{5}$

b) Theo đề bài, $C E ⊥ B D$ tại E nên $\hat{B E C} = 90^{0}$

Xét $Δ A B D$ và $Δ E B C$ có:

$\hat{B A D} = \hat{B E C} = 90^{0}$

$\hat{B_{1}} = \hat{B_{2}}$ (BD là tia phân giác của góc ABC)

Suy ra $Δ A B D ∽ Δ E B C$ (g.g) (đpcm)

Suy ra $\frac{B D}{A D} = \frac{B C}{E C}$ (tỉ số các cạnh tương ứng)

Do đó $B D . E C = A D . B C$ (đpcm)

c) Vì $\frac{D A}{D C} = \frac{B A}{B C}$ nên $\frac{C D}{B C} = \frac{A D}{A B}$ (1)

Vì $Δ A B D ∽ Δ E B C$ (cmt) nên $\frac{A D}{E C} = \frac{A B}{E B}$ suy ra $\frac{A D}{A B} = \frac{E C}{E B}$ (2)

Từ (1) và (2) suy ra $\frac{C D}{B C} = \frac{C E}{B E}$ (đpcm)

d) Xét $Δ C H E$ và $Δ C E B$ có:

$\hat{C H E} = \hat{C E B} = 90^{0}$

$\hat{C}$ chung

Suy ra $Δ C H E ∽ Δ C E B$ (g.g) nên $\frac{C H}{C E} = \frac{C E}{C B}$ suy ra $C H . C B = C E^{2}$ (3)

Tương tự, $Δ C D E ∽ Δ B C E$ (g.g) nên $\frac{E D}{E C} = \frac{C E}{B E}$ suy ra $E D . E B = C E^{2}$ (4)

Từ (3) và (4) suy ra $C H . H B = E D . E B$ (đpcm)

Câu 4 :

Gọi chiều dài của mảnh vườn là x (m), x > 3.

Chiều rộng của mảnh vườn là: x – 3 (m)

Vì chu vi của mảnh vườn hình chữ nhật là 42m nên ta có phương trình:

$\begin{array}{l} 2 [x + (x - 3)] = 42 \\ 2 x - 3 = 21 \\ 2 x = 24 \\ x = 12 (T M) \end{array}$

Vậy chiều dài của mảnh vườn là 12 m.

Câu 5 :

Ta có:

$a_{k} = \frac{2 k + 1}{{(k^{2} + k)}^{2}} = \frac{2 k + 1}{{[k (k + 1)]}^{2}} = \frac{{(k + 1)}^{2} - k^{2}}{k^{2} {(k + 1)}^{2}} = \frac{1}{k^{2}} - \frac{1}{{(k + 1)}^{2}}$

Do đó:

$\begin{array}{l} S_{2024} = a_{1} + a_{2} + a_{3} + . . . + a_{2024} \\ = (\frac{1}{1^{2}} - \frac{1}{2^{2}}) + (\frac{1}{2^{2}} - \frac{1}{3^{2}}) + (\frac{1}{3^{2}} - \frac{1}{4^{2}}) + . . . + (\frac{1}{2023^{2}} - \frac{1}{2024^{2}}) \\ = 1 - \frac{1}{2024^{2}} \\ = \frac{2024^{2} - 1}{2024^{2}} \end{array}$