Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 8 sách Cánh diều năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 1 Toán 8. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 8 Kết nối tri thức bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi học kì 1 Toán 8 Cánh diều có đáp án năm 2025
Đề thi học kì 1 Toán 8 Cánh diều có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 8
Thời gian làm bài: phút
(Đề số 1)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Trong các đơn thức \(M = 2xy{z^2};\,\,N = - 4{y^2}z;\,\,P = - x{z^2};\,\,Q = 5y{z^2},\) đơn thức đồng dạng với đơn thức \( - y{z^2}\) là
A. \(M.\)
B. \(N.\)
C. \(P.\)
D. \(Q.\)
Câu 2. Biết \({x^3} - 12{x^2} + 48x - 64 = 0.\) Giá trị của \(x\) là
A. \(x = - 8.\)
B. \(x = - 4.\)
C. \(x = 4.\)
D. \(x = 8.\)
Câu 3. Biểu thức nào sau đây không phải là phân thức đại số?
A. \(\frac{2}{x}.\)
B. \(\frac{x}{{x + 1}}.\)
C. \({x^2} - 4.\)
D. \[\frac{{x + 1}}{0}.\]
Câu 4. Phân thức nào sau đây là phân thức đối của phân thức \(\frac{{2 - x}}{{3x}}?\)
A. \(\frac{{2 + x}}{{3x}}.\)
B. \(\frac{{x - 2}}{{3x}}.\)
C. \(\frac{{3x}}{{2 - x}}.\)
D. \(\frac{{3x}}{{x - 2}}.\)
Câu 5. Hàm số nào sau đây là hàm số bậc nhất?
A. \(y = 0x + 3.\)
B. \(y = 2{x^2} + 1.\)
C. \(y = - x.\)
D. \(y = 0.\)
|
Câu 6. Điểm \(M\) trên mặt phẳng tọa độ \[Oxy\] (hình bên) có tọa độ là A. \(\left( { - 1;1} \right).\) B. \(\left( { - 2;1} \right).\) C. \(\left( {1; - 1} \right).\) D. \(\left( {1; - 2} \right).\) |
|
Câu 7. Đồ thị của hai hàm số \(y = x + 2\) và \(y = x + 1\)
A. cắt nhau.
B. song song với nhau.
C. trùng nhau.
D. Cả A, B, C đều sai.
Câu 8. Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = - x + 2\) và cắt trục tung tại điểm có tung độ bằng 1 là
A. \(y = x + 1.\)
B. \(y = - x + 1.\)
C. \(y = 1.\)
D. Không có hàm số nào.
Câu 9. Tổng số cạnh bên và cạnh đáy của một hình chóp tứ giác đều là
A. 4.
B. 6.
C. 8.
D. 10.
Câu 10. Một hình chóp tứ giác đều có cạnh đáy là \(a\) và độ dài trung đoạn là \(b\) thì có diện tích xung quanh là
A. \({S_{xq}} = \frac{1}{2}ab.\)
B. \({S_{xq}} = ab.\)
C. \({S_{xq}} = 2ab.\)
D. \({S_{xq}} = 4ab.\)
Câu 11. Tứ giác \(ABCD\) có \(\widehat {A\,\,} = 65^\circ ,\) \(\widehat {B\,} = \widehat C + 23^\circ ,\) \(\widehat {D\,} = 58^\circ .\) Số đo góc \(C\) là
A. \(70^\circ .\)
B. \(107^\circ .\)
C. \(180^\circ .\)
D. \(90^\circ .\)
Câu 12. Trong các hình sau, các hình nào có hai đường chéo vuông góc với nhau?
A. Hình chữ nhật, hình bình hành, hình thoi.
B. Hình bình hành, hình vuông, hình chữ nhật.
C. Hình thoi, hình vuông.
D. Hình thang cân, hình chữ nhật.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Phân tích các đa thức sau thành nhân tử:
a) \({x^3}y + 2{x^2}y + xy;\)
b) \({x^2} - 9 - 4xy + 4{y^2}.\)
Bài 2. (1,5 điểm) Cho biểu thức \(A = \left( {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} + \frac{{{x^2} - 1}}{{9 - {x^2}}}} \right):\left( {2 - \frac{{x + 5}}{{3 + x}}} \right).\)
a) Tìm điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A.\)
c) Tính giá trị của biểu thức \(A\) biết \({x^2} - x - 2 = 0.\)
Bài 3. (1,0 điểm) Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất \(y = ax + b,\) trong đó \(b\) biểu thị chi phí cố định của hoạt động kinh doanh và hệ số \(a\) biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là \(1,8\) triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí \(y\) (triệu đồng) để sản xuất \(x\) (xe đạp) trong một ngày.
b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?
Bài 4. (3,0 điểm)
1) Hình vẽ dưới đây mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng 1 m; phần trên có dạng hình chóp tứ giác đều với chiều cao bằng \[0,6\] m.
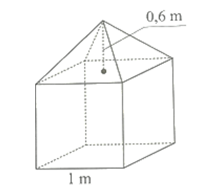
Cần phải chuẩn bị bao nhiêu tấn xi măng và bao nhiêu mét khối nước để làm khối bê tông đó? Biết rằng 1 m3 bê tông mác 200 cần khoảng \[350,55\] kg xi măng và 185 l nước.
2) Cho tam giác \[ABC\] vuông tại \[A\] có \[AB < AC,\] đường cao \[AH.\] Kẻ \[HD\] vuông góc với \[AB\] tại \(D,\) \[HE\] vuông góc với \[AC\] tại \(E.\)
a) Tứ giác \[ADHE\] là hình gì? Vì sao?
b) Tính diện tích của tứ giác \[ADHE\] nếu \[AD = 4\,\,{\rm{cm}};\,\,AH = 5\,\,{\rm{cm}}{\rm{.}}\]
c) Lấy hai điểm \(I\) và \(K\) sao cho \(D\) là trung điểm của \(BI\) và \(D\) cũng là trung điểm của \(HK.\) Chứng minh tứ giác \[BKIH\] là hình bình hành; \[AK\] vuông góc với \[IH.\]
Bài 5. (0,5 điểm) Cho \({a^3} + {b^3} + {c^3} = 3abc\) và \(a + b + c \ne 0.\) Tính giá trị của biểu thức:
\(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}}.\)
-----HẾT-----
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
D |
C |
D |
B |
C |
B |
A |
B |
C |
C |
B |
C |
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm)
|
a) \({x^3}y + 2{x^2}y + xy\) \( = xy \cdot \left( {{x^2} + 2x + 1} \right)\) \( = xy \cdot {\left( {x + 1} \right)^2}.\) |
b) \({x^2} - 9 - 4xy + 4{y^2}\) \( = \left( {{x^2} - 4xy + 4{y^2}} \right) - 9\) \( = {\left( {x - 2y} \right)^2} - {3^2}\) \( = \left( {x - 2y - 3} \right)\left( {x - 2y + 3} \right).\) |
Bài 2. (1,5 điểm)
a) Ta có \(9 - {x^2} = \left( {3 - x} \right)\left( {3 + x} \right).\)
\[2 - \frac{{x + 5}}{{3 + x}} = \frac{{2\left( {3 + x} \right) - \left( {x + 5} \right)}}{{3 + x}} = \frac{{6 + 2x - x - 5}}{{3 + x}} = \frac{{x + 1}}{{x + 3}}.\]
Điều kiện xác định của biểu thức \(A\) là \(\left\{ \begin{array}{l}x + 3 \ne 0\\x - 3 \ne 0\\9 - {x^2} \ne 0\\2 - \frac{{x + 5}}{{3 + x}} \ne 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + 3 \ne 0\\x - 3 \ne 0\\x + 1 \ne 0\end{array} \right.\) tức là \(\left\{ \begin{array}{l}x \ne - 3\\x \ne 3\\x \ne - 1\end{array} \right.\)
Vậy điều kiện xác định của biểu thức \(A\) là \(x \ne - 3,x \ne 3\) và \(x \ne - 1.\)
b) Với \(x \ne - 3,x \ne 3\) và \(x \ne - 1\) ta có:
\(A = \left( {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} + \frac{{{x^2} - 1}}{{9 - {x^2}}}} \right):\left( {2 - \frac{{x + 5}}{{3 + x}}} \right)\)
\( = \left[ {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} - \frac{{{x^2} - 1}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}} \right]:\frac{{x + 1}}{{x + 3}}\)
\( = \frac{{x\left( {x - 3} \right) - 2\left( {x + 3} \right) - \left( {{x^2} - 1} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}:\frac{{x + 1}}{{x + 3}}\)
\( = \frac{{{x^2} - 3x - 2x - 6 - {x^2} + 1}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\frac{{x + 3}}{{x + 1}}\)
\[ = \frac{{ - 5x - 5}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\frac{{x + 3}}{{x + 1}}\]
\[ = \frac{{ - 5\left( {x + 1} \right)}}{{\left( {x - 3} \right)\left( {x + 1} \right)}} = \frac{{ - 5}}{{x - 3}}.\]
Vậy với \(x \ne - 3,x \ne 3\) và \(x \ne - 1\) thì \(A = \frac{{ - 5}}{{x - 3}}.\)
c) Với \({x^2} - x - 2 = 0\) ta có \({x^2} - 2x + x - 2 = 0\)
\(x\left( {x - 2} \right) + \left( {x - 2} \right) = 0\)
\(\left( {x - 2} \right)\left( {x + 1} \right) = 0\)
Suy ra \(x - 2 = 0\) hoặc \(x + 1 = 0\)
\(x = 2\) (thỏa mãn điều kiện) hoặc \(x = - 1\) (không thỏa mãn điều kiện)
Thay \(x = 2\) vào biểu thức \(A = \frac{{ - 5}}{{x - 3}}\) ta được:
\(A = \frac{{ - 5}}{{2 - 3}} = \frac{{ - 5}}{{ - 1}} = 5.\)
Vậy nếu \({x^2} - x - 2 = 0\) thì \(A = 5.\)
Bài 3. (1,0 điểm)
a) Công thức của hàm số bậc nhất biểu thị chi phí \(y\) (triệu đồng) để sản xuất \(x\) (xe đạp) trong một ngày là:
\(y = 1,8x + 36\) (triệu đồng).
b) Do chi phí trong ngày đó là 72 triệu đồng nên \(y = 72\) (triệu đồng).
Thay \(y = 72\) vào công thức \(y = 1,8x + 36\) ta có:
\(1,8x + 36 = 72\)
\(1,8x = 36\)
\(x = 20\)
Vậy với chi phí là 72 triệu đồng thì trong ngày đó có thể sản xuất được 20 chiếc xe đạp.
Bài 4. (3,0 điểm)
1) Thể tích phần dưới (có dạng hình lập phương) của khối bê tông là: \[{1^3} = 1\] (m3).
Thể tích phần trên (có dạng hình chóp tứ giác đều) của khối bê tông là:
\(\frac{1}{3} \cdot {1^2} \cdot 0,6 = 0,2\) (m3).
Thể tích của khối bê tông là: \[1 + 0,2 = 1,2\] (m3).
Đổi \[350,55\] kg \[ = 0,35055\] tấn; 185 lít \[ = 0,185\] m3.
Khối lượng xi măng cần dùng để làm khối bê tông đó là:
\[1,2 \cdot 0,35055 = 0,42066\] (tấn).
Lượng nước cần dùng để làm khối bê tông đó là:
\[1,2 \cdot 0,185 = 0,222\] (m3).
2)
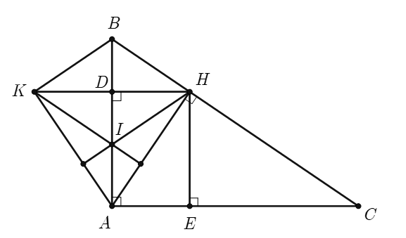
a) Vì \(\Delta ABC\) vuông tại \(A\) nên \(\widehat {BAC} = 90^\circ \) hay \(\widehat {DAE} = 90^\circ \).
Ta có \(HD \bot AB\); \(HE \bot AC\) nên \(\widehat {HDA} = 90^\circ \); \(\widehat {HEA} = 90^\circ \).
Tứ giác \(ADHE\) có \[\widehat {DAE} = \widehat {HDA} = \widehat {HEA} = 90^\circ \].
Do đó, tứ giác \(ADHE\) là hình chữ nhật.
b) Xét \(\Delta AHD\) vuông tại \(D\), áp dụng định lý Pythagore, ta có:
\(A{H^2} = A{D^2} + D{H^2}\) hay \(25 = 16 + D{H^2}\)
Suy ra \(D{H^2} = 9\) nên \(DH = 3\,\,\left( {{\rm{cm}}} \right){\rm{.}}\)
Tứ giác \(ADHE\) là hình chữ nhật nên ta có
\({S_{ADHE}} = AD\,.\,DH = 4\,.\,3 = 12\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy diện tích tứ giác \(ADHE\) bằng \(12\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
c) Xét tứ giác \(BKIH\) có \(D\) là trung điểm của hai đường chéo \(BI\) và \(HK\) nên \(BKIH\) là hình bình hành (dấu hiệu nhận biết).
Do đó \(KI\,{\rm{//}}\,BH.\)
Mà \(AH \bot BH\) suy ra \(KI \bot AH.\)
Xét \(\Delta AHK\) có \(AD \bot KH;\,\,KI \bot AH\) và \(AD\) cắt \(KI\) tại \(I.\)
Do đó, \(I\) là trực tâm của tam giác \(AKH\) suy ra \(HI \bot AK.\)
Bài 5. (0,5 điểm)
Ta có:
\({a^3} + {b^3} + {c^3} = 3abc\)
\({a^3} + {b^3} + {c^3} - 3abc = 0\)
\({\left( {a + b} \right)^3} - 3ab\left( {a + b} \right) + {c^3} - 3abc = 0\)
\({\left( {a + b} \right)^3} + {c^3} - 3ab\left( {a + b + c} \right) = 0\)
\({\left( {a + b + c} \right)^3} - 3\left( {a + b} \right)c\left( {a + b + c} \right) - 3ab\left( {a + b + c} \right) = 0\)
\(\left( {a + b + c} \right)\left[ {{{\left( {a + b + c} \right)}^2} - 3ac - 3bc - 3ab} \right] = 0\)
\(\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ac - bc - ab} \right) = 0\)
Suy ra \({a^2} + {b^2} + {c^2} - ac - bc - ab = 0\) (do \(a + b + c \ne 0).\)
Nên \[{a^2} + {b^2} + {c^2} = ab + bc + ca.\]
Khi đó ta có \(N = \frac{{{a^2} + {b^2} + {c^2}}}{{{{\left( {a + b + c} \right)}^2}}} = \frac{{{a^2} + {b^2} + {c^2}}}{{{a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)}}\)
\( = \frac{{{a^2} + {b^2} + {c^2}}}{{{a^2} + {b^2} + {c^2} + 2\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{{{a^2} + {b^2} + {c^2}}}{{3\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{1}{3}.\)
Vậy \(N = \frac{1}{3}.\)
-----HẾT-----
Đề thi học kì 1 Toán 8 Cánh diều có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 8
Thời gian làm bài: phút
(Đề số 2)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Cho các đơn thức và . Hai đơn thức thu gọn trong các đơn thức đã cho là:
A. A và B.
B. A và C.
C. A và D.
D. B và C.
Câu 2. Biểu thức cần điền vào chỗ trống để có hằng đẳng thức đúng là
A. x.
B. -x.
C. 2x.
D. -2x.
Câu 3. Cho phân thức với B ≠ 0. Nhận định nào sau đây là đúng?
A. .
B. .
C. , N ≠ 0.
D. , M ≠ 0.
Câu 4. Phân thức đối của phân thức là
A. .
B. .
C. .
D. .
Câu 5. Cho hàm số y = f(x) = 2x2 - 1. Khẳng định nào sau đây là đúng?
A. f(-1) = -3.
B. f(1) = 1.
C. f(-1) = -1.
D. f(1) = 3.
|
Câu 6. Cho điểm A và B trong mặt phẳng tọa độ Oxy như hình bên. Khẳng định nào sau đây là đúng? A. N (-3; 2). B. N(2; -3). C. M (1; -2). D. M (-1; 2). |
|
Câu 7. Cho hai đường thẳng d: y = ax + b (a c 0) và d': y = a'x + b' (a' ≠ 0). Với điều kiện nào sau đây thì hai đường thẳng d và d' song song?
A. a = a'.
B. a = a' và b = b'.
C. a ≠ a'.
D. a = a' và b ≠ b'.
Câu 8. Góc tạo bởi đường thẳng y = -2x + 1 với trục Ox là
A. góc nhọn.
B. góc vuông.
C. góc tù.
D. góc bẹt.
Câu 9. Tổng số cạnh bên và cạnh đáy của một hình chóp tứ giác đều là
A. 4.
B. 6.
C. 8.
D. 10.
Câu 10. Một hình chóp tam giác đều có cạnh đáy là a và độ dài trung đoạn là b thì có diện tích xung quanh là
A. .
B. Sxq = ab.
C. .
D. Sxq = 3ab.
Câu 11. Một hình thang vuông có một góc bằng 75° góc còn lại không vuông của hình thang đó có số đo là
A. 25°.
B. 75°.
C. 105°.
D. 125°.
Câu 12. Hình thoi cần thêm yếu tố nào để trở thành hình vuông?
A. Hai đường chéo vuông góc.
B. Hai đường chéo bằng nhau.
C. Hai cạnh kề bằng nhau.
D. Một đường chéo là tia phân giác của một góc.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm) Phân tích các đa thức sau thành nhân tử:
a) .
b) .
Bài 2. (1,5 điểm) Cho biểu thức .
a) Viết điều kiện xác định của biểu thức N.
b) Rút gọn biểu thức N.
c) Tính giá trị của biểu thức N khi |x| = 2.
Bài 3. (1,0 điểm) Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là <![if !vml]>![]() <![endif]> triệu đồng.
<![endif]> triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày.
b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?
Bài 4. (3,0 điểm)
|
1) Bạn Hà làm một cái lồng đèn hình quả trám (xem hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy 20 cm, cạnh bên 26 cm, khoảng cách giữa hai đỉnh của hai hình chóp là 30 cm. a) Tính thể tích của lòng đèn. b) Bạn Hà muốn dán giấy mờ lên cái lòng đèn hình quả trám này thì cần phải chuẩn bị bao nhiêu mét vuông giấy (bỏ qua các mép dán)? |
|
2) Cho tam giác ABC nhọn có AB < AC. Gọi N là trung điểm của AC. Lấy điểm D trên tia BN sao cho BN = ND. Kẻ .
a) Chứng minh N là trung điểm của PQ.
b) Tam giác ABC cần thêm điều kiện gì để tứ giác ABCD là hình vuông.
Bài 5. (0,5 điểm) Cho hai số x, y khác 0 thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức A = xy + 2024.
-----HẾT-----
ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
C |
A |
C |
C |
B |
B |
D |
C |
C |
C |
C |
B |
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm):
Bài 2. (1,5 điểm):
a) Ta có x2 - 1 = (x - 1)(x + 1).
Điều kiện xác định của biểu thức N là x + 1 ≠ 0, x - 1 ≠ 0, 2 + x ≠ 0 và x2 - 1 ≠ 0
Hay x ≠ -1, x ≠ 1 và x ≠ 2.
Vậy biểu thức N xác định khi x ≠ -1, x ≠ 1 và x ≠ 2.
b) Với x ≠ -1, x ≠ 1 và x ≠ -2 ta có:
Vậy với x ≠ -1, x ≠ 1 và x ≠ -2 thì .
c) Ta có |x| = 2 suy ra x = 2 (thỏa mãn điều kiện) hoặc x = -2 (không thỏa mãn điều kiện).
Thay x = 2 vào biểu thức , ta được:
.
Vậy khi .
Bài 3. (1,0 điểm):
a) Công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày là:
y = 1,8x + 36 (triệu đồng).
b) Do chi phí trong ngày đó là 72 triệu đồng nên y = 72 (triệu đồng).
Thay y = 72 vào công thức y = 1,8x + 36 ta có:
1,8x + 36 = 72
1,8x = 36
x = 20
Vậy với chi phí là 72 triệu đồng thì trong ngày đó có thể sản xuất được 20 chiếc xe đạp.
Bài 4. (3,0 điểm):
1)
a) Chiều cao của mỗi hình chóp tứ giác đều là 30:2 = 15 (cm).
Thể tích của lồng đèn quả trám là: (cm3).
b) Một nửa lồng đèn được mô tả bởi hình chóp S.ABCD với các kích thước như hình vẽ.
2)
Bài 5. (0,5 điểm):
Theo đề bài: suy ra
Do đó hay .
Khi đó .
Vậy giá trị nhỏ nhất của biểu thức A là 2 016 khi (x; y) ∈ {(2;-4);(-2;4)}.
-----HẾT-----
Đề thi học kì 1 Toán 8 Cánh diều có đáp án - Đề 3
Phòng Giáo dục và Đào tạo ...
Đề thi học kì 1 - Cánh diều
Năm học 2024 - 2025
Môn: Toán lớp 8
Thời gian làm bài: phút
(Đề số 3)
Câu 1 : Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Câu 2 : Tính giá trị của biểu thức: 302 + 452 - 252 + 60.45 được kết quả là
Câu 3 : Giá trị của biểu thức khi x = -2 là:
Câu 4 : Hiệu của biểu thức bằng:
Câu 5 : Cho . Đa thức P là:
Câu 6 : Cho ABCD là hình bình hành với các điều kiện như trên hình vẽ.
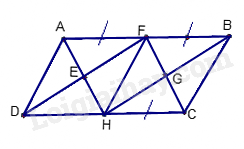
Trên hình này có:
Câu 7 : Tứ giác là hình chữ nhật nếu:
Câu 8 : Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích xung quanh của hình chóp.
Câu 9 : Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm3; chiều cao của hình chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là (Làm tròn đến hàng đơn vị)
Câu 10 : Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Câu 11 : Hình bình hành ABCD là hình chữ nhật khi:
Câu 12 : Hiện tại bạn Nam đã để dành được một số tiền là 800 000 đồng. Bạn Nam đang có ý định mua một chiếc xe đạp trị giá 2 640 000 đồng, nên hàng ngày, bạn Nam đều để dành ra 20000 đồng. Gọi m (đồng) là số tiền bạn Nam tiết kiệm được sau t ngày.
Thiết lập hàm số của m theo t.
Hỏi sau bao nhiêu lâu kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó.
Câu 13 : Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
Câu 14 : Cho đường thẳng d : y = -3x + 2. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là :
Câu 1 : Cho phân thức:
a) Với điều kiện nào của x thì giá trị của phân thức A được xác định?
b) Rút gọn phân thức A.
c) Tính giá trị nguyên của x để phân thức A có giá trị nguyên.
Câu 2 : a) Tìm x, biết: x2 + 3x = 0
b) Tìm giá trị nhỏ nhất của biểu thức: x2 4x + 7
Câu 3 : Một xí nghiệp dự tính chuyển hàng bằng 2 chiếc xe tải và đang phân vân giữa việc mua hẳn 2 chiếc xe tải hoặc thuê 2 chiếc xe tải. Nếu mua hẳn 2 xe và mỗi xe có giá trị là 200 000 000 đồng thì mỗi xí nghiệp phải tốn 5 000 000 đồng để trả lương cho tất cả tài xế. Nếu thuê xe thì giá để thuê 1 chiếc xe chở hàng là 10 000 000 đồng/ngày (đã bao gồm tiền công cho tài xế).
a) Gọi C là tổng số tiền xí nghiệp bỏ ra để vận chuyển hàng sau n ngày. Lập hàm số biểu diễn C theo n đối với mỗi phương án.
b) Nếu xe muốn vận chuyển 1600 thùng hàng và mỗi ngày chỉ chở được 80 thùng hàng thì phương án nào sẽ tiết kiệm hơn ?
Câu 4 : 1. Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (Không tính phần viền xung quanh)
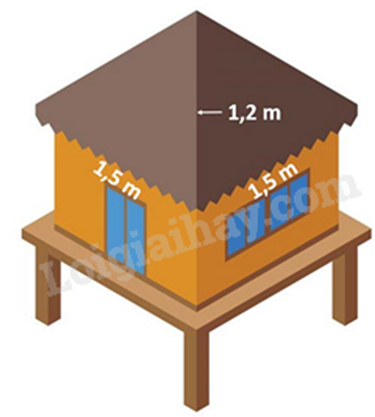
2. Cho tam giác vuông tại có . Gọi là trung điểm của , kẻ vuông góc với tại , vuông góc với tại .
a) Chứng minh .
b) Chứng minh tứ giác là hình bình hành.
c) Gọi là đường cao của tam giác (). Chứng minh tứ giác là hình thang cân.
Câu 5 : Tìm để biểu thức có giá trị là một số nguyên tố.
ĐÁP ÁN
| Câu 1-D | Câu 2-D | Câu 3-D | Câu 4-A | Câu 5-C | Câu 6-D | Câu 7-D |
| Câu 8-B | Câu 9-C | Câu 10-C | Câu 11-B | Câu 12-a) A; b) A | Câu 13-D | Câu 14-D |
Câu 1 :
a) Phân thức A xác định khi và chỉ khi
b) Ta có:
c) Phân thức A có giá trị nguyên khi và chỉ khi nguyên, hay .
Ta có bảng giá trị sau:
|
1 + 2x |
-1 |
1 |
|
x |
-1 (TM) |
0 (TM) |
|
|
-1 |
1 |
Vậy thì phân thức A có giá trị nguyên.
Câu 2 :
a)
Vậy x = 0 hoặc x = -3.
b) Ta có:
Vì với mọi nên với mọi .
Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức x2 4x + 7.
Vậy giá trị nhỏ nhất của x2 4x + 7 bằng 3 khi x – 2 = 0 hay x = 2.
Câu 3 :
a)
Phương án 1: Tổng số tiền C sau n ngày là:
C = 200 000 000 + 5 000 000.n (đồng)
C = 200 + 5.n (triệu đồng)
Phương án 2: Tổng số tiền C sau n ngày là:
C = 10 000 000.n (đồng)
C = 10.n (triệu đồng)
b) Mỗi ngày chở được 80 thùng trong 1600 thùng thì phải chở trong:
1600 : 80 = 20 (ngày)
Khi đó tổng tiền phải trả theo:
+ PA 1 là: C = 200 + 5.20 = 300 (triệu đồng)
+ PA 2 là: C = 10.20 = 200 (triệu đồng)
=> Phương án 2 tiết kiệm hơn.
Câu 4 :
1.
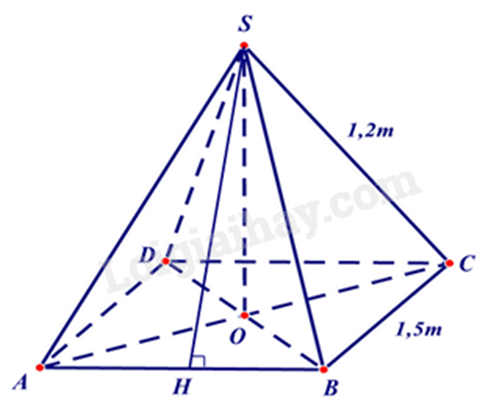
Ta có hình vẽ minh họa cho mái nhà của chòi như hình trên.
Gọi SH là đường cao của tam giác SAB nên SH là trung đoạn của hình chóp S.ABCD.
Vì S.ABCD là hình chóp tứ giác đều nên SAB là tam giác cân. Do đó SA = SB = 1,2m. Khi đó SH là đường cao đồng thời là đường trung tuyến nên AH = BH = AB = .1,5 = 0,75(m).
Áp dụng định lí Pythagore vào tam giác vuông SHB, ta có:
Diện tích vải bạc cần dùng để phủ mái chòi chính là diện tích xung quanh của hình chóp tứ giác đó.
Diện tích xung quanh của hình chóp là:
.
Vậy diện tích vải bạc cần dùng để phủ mái chòi là 3m2.
2.
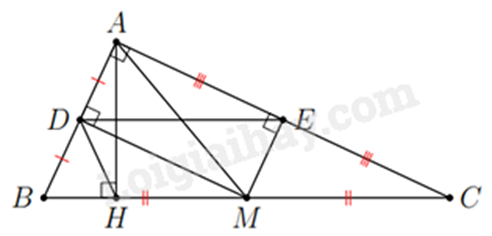
a) Xét tứ giác ADME có:
(tam giác ABC vuông tại A)
( vuông góc với tại , vuông góc với tại )
=> ADME là hình chữ nhật (tứ giác có 3 góc vuông).
b) Xét tam giác ABC vuông tại A có M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC nên AM = MC =
Khi đó tam giác AMC cân tại M. Mà ME vuông góc với AC nên ME là đường cao đồng thời là đường trung tuyến của tam giác AMC suy ra E là trung điểm của AC AE = EC. (1)
ADME là hình chữ nhật nên DM // AE và DM = AE (2)
Từ (1) và (2) suy ra DM // EC và DM = EC, do đó tứ giác DMCE là hình bình hành.
c) DMCE là hình bình hành nên DE // MC => DE // HM (H thuộc đường thẳng CM)
=> DHME là hình thang.
Xét tam giác AMB có AM = BM nên tam giác AMB cân tại M. Mà MD vuông góc với AB nên MD đường cao đồng thời là đường trung tuyến của tam giác ABM suy ra D là trung điểm của AB.
Xét tam giác ABH vuông tại H, D là trung điểm của AB nên HD là đường trung tuyến ứng với cạnh huyền của tam giác AHB => .
Mà ADME là hình chữ nhật nên AD = ME suy ra HD = ME.
Hình thang DHME có HD = ME nên DHME là hình thang cân.
Câu 5 :
Ta có:
Để A là số nguyên tố thì A chỉ có 2 ước là 1 và chính nó.
có ước là 1 và chính nó khi và chỉ khi hoặc .
Trường hợp 1. Với , ta có:
Khi đó
Trường hợp 2. Với , ta có:
(không thỏa mãn vì ).
Vậy n = 3 thì biểu thức có giá trị là một số nguyên tố.