Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 8 sách Chân trời sáng tạo năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 1 Toán 8. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 8 Chân trời sáng tạo bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi học kì 1 Toán 8 Chân trời sáng tạo có đáp án năm 2024
Đề thi học kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 1
Phòng Giáo dục và Đào tạo ...
Đề thi học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 8
Thời gian làm bài: phút
(Đề số 1)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức thu gọn?
A. \( - {x^4}{y^3}x.\)
B. \(\frac{1}{3}{x^4}{y^3}.\)
C. \(\frac{1}{3}{x^2}{y^2}yz.\)
D. \(\frac{{ - 1}}{3}x{y^4}zxy.\)
Câu 2. Trong các đẳng thức dưới đây, đẳng thức nào là đẳng thức đúng?
A. \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}.\)
B. \({\left( {A + B} \right)^2} = {A^2} + AB + {B^2}.\)
C. \({\left( {A + B} \right)^2} = {A^2} + {B^2}.\)
D. \({\left( {A + B} \right)^2} = {A^2} - 2AB + {B^2}.\)
Câu 3. Với điều kiện nào của \[x\] thì phân thức \(\frac{{{{\left( {x - 1} \right)}^3}}}{{\left( {x - 2} \right)\left( {x + 3} \right)}}\) có nghĩa?
A. \[x \le 2\].
B. \(x \ne 2\,;\,\,x \ne - 3\).
C. \[x = 2\].
D. \[x \ne 2\].
Câu 4. Đường cao của hình chóp tam giác đều là
A. Đoạn thẳng kẻ từ đỉnh của hình chóp đến trọng tâm của tam giác đáy.
B. Đoạn thẳng kẻ từ đỉnh của hình chóp đến trung điểm của một cạnh đáy.
C. Đoạn thẳng kẻ từ đỉnh của hình chóp đến một điểm tùy ý nằm trong mặt đáy.
D. Đoạn thẳng kẻ từ đỉnh của hình chóp đến một điểm bất kì trên cạnh bên của hình chóp.
Câu 5. Các mặt bên của hình chóp tứ giác đều \[S.BCDM\] là
|
A. \(SCD\,;\,\,SCB\,;\,\,SBM\). B. \(SCD\,;\,\,SC\,;\,\,SMD\). C. \(SCD\,;\,\,SCB\,;\,\,SBM\,;\,\,SMD\). D. \(SCD\,;\,\,SCB\,;\,\,SBM\,;\,\,SBD\). |
|
Câu 6. Cho hình chóp tam giác đều, biết chiều cao của hình chóp là \({\rm{4}}\;{\rm{cm}}\), tam giác đáy có cạnh \({\rm{5}}\;{\rm{cm}}\) và chiều cao \(\frac{{5\sqrt 3 }}{2}\;{\rm{cm}}\). Thể tích của khối chóp tam giác đều đó là
A. \[{\rm{25}}\sqrt {\rm{3}} \;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
B. \[\frac{{{\rm{125}}\sqrt {\rm{3}} }}{{\rm{4}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
C. \[\frac{{{\rm{25}}\sqrt {\rm{3}} }}{{\rm{3}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
D. \[\frac{{{\rm{25}}\sqrt {\rm{3}} }}{{{\rm{14}}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
Câu 7. Cho hình chóp tứ giác đều có thể tích bằng \({\rm{50}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\) chiều cao là \({\rm{6}}\;{\rm{cm}}\). Độ dài cạnh đáy của hình chóp đó là
A. \({\rm{50}}\;{\rm{cm}}\).
B. \({\rm{5}}\;{\rm{cm}}\).
C. \[{\rm{25}}\;{\rm{cm}}\].
D. \({\rm{5}}\;{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Câu 8. Nhận xét nào sau đây là đúng?
A. Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.
B. Trong tam giác vuông, cạnh huyền là cạnh bé nhất.
C. Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền.
D. Trong tam giác vuông, cạnh góc vuông lớn hơn cạnh huyền.
Câu 9. Cho tứ giác \[ABCD\] có \(\widehat A + \widehat B = 140^\circ \). Khi đó \(\widehat C + \widehat D = ?\)
A. \(200^\circ \).
B. \(220^\circ \).
C. \(160^\circ \).
D. \(130^\circ \).
|
Câu 10. Tứ giác \[ABCD\] trong hình vẽ bên là A. hình vuông. B. hình chữ nhật. C. hình thoi. D. hình bình hành. |
|
Câu 11. Trong các trường hợp sau, trường hợp nào là thu thập dữ liệu gián tiếp?
A. Phỏng vấn các bạn học sinh về tình hình bạo lực học đường.
B. Lập phiếu hỏi về các món ăn mà các bạn học sinh trong lớp yêu thích.
C. Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam.
D. Làm thí nghiệm để xác định tính chất hóa học của oxygen.
|
Câu 12. Hình vẽ bên là biểu đồ về diện tích các châu lục trên thế giới. Hỏi Châu Mỹ chiếm bao nhiêu phần trăm tổng diện tích của cả sáu châu lục đó? A. \(20\% \). B. \(28\% \). C. \(30\% \). D. \(7\% \). |
|
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Thực hiện phép tính:
a) \[\left( {4{x^3}{y^2} - 8{x^2}y + 10xy} \right):\left( {2xy} \right)\];
b) \[\left( {3 - x} \right)\left( {3 + x} \right) + {\left( {x--5} \right)^2}\];
c) \[\frac{x}{{x + 1}} + \frac{{2x + 5}}{{x - 1}} - \frac{{3{x^2} - 1}}{{{x^2} - 1}}\].
Bài 2. (1,0 điểm) Phân tích các đa thức sau thành nhân tử:
a) \(25{x^2}\left( {x - 3y} \right) - 15\left( {3y - x} \right);\)
b) \({x^4} - 5{x^2} + 4.\)
Bài 3. (1,5 điểm) Tỉ lệ phần trăm kết quả phỏng vấn \[1\,\,000\] khách hàng về sự lựa chọn món ăn của một cửa hàng được thể hiện trong biểu đồ sau:
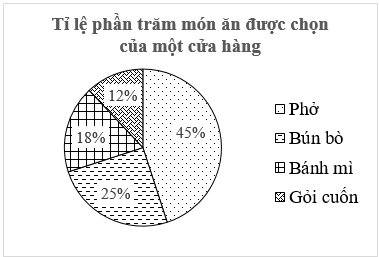
a) Cửa hàng đã thu thập dữ liệu được biểu diễn trong biểu đồ trên bằng phương pháp nào? Đây là phương pháp thu thập trực tiếp hay gián tiếp?
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:
|
Món ăn |
Tỉ lệ phần trăm |
|
Phở |
? |
|
Bún bò |
? |
|
Bánh mì |
? |
|
Gỏi cuốn |
? |
c) Nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì cửa hàng nên ưu tiên chọn món nào? Tại sao?
Bài 4. (2,5 điểm)
|
1. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\), điện thoại có chiều rộng là \[7\,\,{\rm{cm;}}\] chiều dài là \[15,5{\rm{ cm}}.\] Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị). |
|
2. Cho tam giác \(ABC\) nhọn có \(AB < AC\,.\) Gọi \(N\) là trung điểm của \(AC\,.\) Lấy điểm \(D\) trên tia \(BN\) sao cho \(BN = ND\,.\) Kẻ \(AP \bot BC\,,\,\,CQ \bot AD\,.\)
a) Chứng minh \(N\) là trung điểm của \(PQ\).
b) Tam giác \(ABC\) cần thêm điều kiện gì để tứ giác \(ABCD\) là hình vuông.
Bài 5. (0,5 điểm) Cho ba số \[a,\,\,b,\,\,c\] đôi một khác nhau và thỏa mãn:
\[{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}.\]
Tính giá trị biểu thức \[T = \frac{{{a^3}{b^3} + {b^3}{c^3} + {c^3}{a^3}}}{{3{a^2}{b^2}{c^2}}} + \left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{c}{b}} \right).\]
−−−−−HẾT−−−−−
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1 – TOÁN 8
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
D |
A |
B |
A |
C |
C |
B |
D |
B |
D |
C |
B |
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
|
a) \[\left( {4{x^3}{y^2} - 8{x^2}y + 10xy} \right):\left( {2xy} \right)\] \[ = 4{x^3}{y^2}:\left( {2xy} \right) - 8{x^2}y:\left( {2xy} \right) + 10xy:\left( {2xy} \right)\] \[ = {\rm{ }}2{x^2}y - 4x + 5.\]
|
b) \[\left( {3 - x} \right)\left( {3 + x} \right) + {\left( {x--5} \right)^2}\] \[ = \left( {9 - {x^2}} \right) + \left( {{x^2} - 10x + 25} \right)\] \[ = 9 - {x^2} + {x^2} - 10x + 25\] \[ = \left( {{x^2} - {x^2}} \right) - 10x + \left( {25 + 9} \right)\] \[ = - 10x + 34\]. |
c) \[\frac{x}{{x + 1}} + \frac{{2x + 5}}{{x - 1}} - \frac{{3{x^2} - 1}}{{{x^2} - 1}}\]
\[ = \frac{x}{{x + 1}} + \frac{{2x + 5}}{{x - 1}} - \frac{{3{x^2} - 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\]
\[ = \frac{{x\left( {x - 1} \right) + \left( {2x + 5} \right)\left( {x + 1} \right) - \left( {3{x^2} - 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\]
\[ = \frac{{{x^2} - x + 2{x^2} + 2x + 5x + 5 - 3{x^2} + 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\]
\[ = \frac{{6x + 6}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{6\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{6}{{x - 1}}\].
Bài 2. (1,0 điểm)
|
a) \(25{x^2}\left( {x - 3y} \right) - 15\left( {3y - x} \right)\) \( = 25{x^2}\left( {x - 3y} \right) + 15\left( {x - 3y} \right)\) \( = \left( {x - 3y} \right)\left( {25{x^2} + 15} \right)\) \( = 5\left( {x - 3y} \right)\left( {5{x^2} + 3} \right).\) |
b) \({x^4} - 5{x^2} + 4\) \( = {x^4} - {x^2} - 4{x^2} + 4\) \( = {x^2}\left( {{x^2} - 1} \right) - 4\left( {{x^2} - 1} \right)\) \( = \left( {{x^2} - 4} \right)\left( {{x^2} - 1} \right)\) \( = \left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right)\left( {x + 1} \right).\) |
Bài 3. (1,5 điểm)
a) Cửa hàng đã thu thập dữ liệu được biểu diễn trong biểu đồ trên bằng phương pháp phỏng vấn 1 000 khách hàng. Đây là phương pháp thu thập trực tiếp.
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:
|
Món ăn |
Tỉ lệ phần trăm |
|
Phở |
\[45\% \] |
|
Bún bò |
\[25\% \] |
|
Bánh mì |
\[18\% \] |
|
Gỏi cuốn |
\[12\% \] |
c) Nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì cửa hàng nên ưu tiên chọn món Phở. Vì đây là món ăn được khách hàng lựa chọn nhiều nhất (chiếm \[45\% ).\]
Bài 4. (2,5 điểm)
1. Áp dụng định lí Pythagore vào tam giác \[ABC\] vuông tại \[A\], ta có:
\(B{C^2} = A{C^2} + A{B^2} = {\left( {15,5} \right)^2} + {7^2} = 289,25\)
Suy ra \[BC = \sqrt {289,25} \approx 17\,\,{\rm{(cm)}}\].
Vì \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\) nên chiếc điện thoại theo hình vẽ có: \(\frac{{17}}{{2,54}} \approx 7\,\,({\rm{inch)}}\)
Vậy chiếc điện thoại theo hình vẽ khoảng 7 inch.
2.
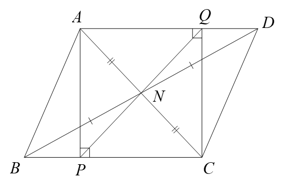
a) Ta có \(AP \bot BC;\,\,AQ\parallel BC\) suy ra \(AP \bot AQ\) hay \(\widehat {PAQ} = 90^\circ \).
Vì \(AP \bot BC\,,\,\,CQ \bot AD\,\) nên \(\widehat {APQ} = 90^\circ ;\,\,\widehat {AQC} = 90^\circ \).
Tứ giác \(APCQ\) có \(\widehat {PAQ} = 90^\circ \); \(\widehat {APQ} = 90^\circ ;\,\,\widehat {AQC} = 90^\circ \) nên là hình chữ nhật.
Khi đó hai đường chéo \(AC,\,\,PQ\) cắt nhau tại trung điểm của mỗi đường.
Mà \(N\) là trung điểm của \(AC\) nên \(N\) là trung điểm của \(PQ\).
b) Tứ giác \(ABCD\) có hai đường chéo \(AC,\,\,BD\) cắt nhau tại trung điểm \(N\) của mỗi đường nên là hình bình hành.
Để tứ giác \(ABCD\) là hình vuông thì ta cần \(AB \bot BC,\,\,AB = BC\) hay \(\Delta ABC\) vuông cân tại \(B\,.\)
Vậy để tứ giác \(ABCD\) là hình vuông thì tam giác \(ABC\) vuông cân tại \(B\,.\)
Bài 5. (0,5 điểm
Ta có \[{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca\]
Theo bài, \[{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}\] nên suy ra \[ab + bc + ca = 0.\]
Đặt \[x = ab;y = bc;z = ca.\]
Khi đó \[x + y + z = 0.\] Suy ra \(x + y = - z;\,\,y + z = - x;\,\,z + x = - y.\)
Xét \[\left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{c}{b}} \right)\]
\[ = \left( {1 + \frac{{ab}}{{bc}}} \right)\left( {1 + \frac{{bc}}{{ca}}} \right)\left( {1 + \frac{{ca}}{{ab}}} \right)\]
\[ = \left( {1 + \frac{x}{y}} \right)\left( {1 + \frac{y}{z}} \right)\left( {1 + \frac{z}{x}} \right)\]
\[ = \left( {\frac{{y + x}}{y}} \right)\left( {\frac{{z + y}}{z}} \right)\left( {\frac{{x + z}}{x}} \right)\]
\[ = \frac{{ - z}}{y}.\frac{{ - x}}{z}.\frac{{ - y}}{x} = - 1.\]
Xét \[\frac{{{a^3}{b^3} + {b^3}{c^3} + {c^3}{a^3}}}{{3{a^2}{b^2}{c^2}}} = \frac{{{x^3} + {y^3} + {z^3}}}{{3xyz}}\]
\[ = \frac{{{{\left( {x + y} \right)}^3} - 3xy\left( {x + y} \right) + {z^3}}}{{3xyz}}\]
\[ = \frac{{{{\left( { - z} \right)}^3} - 3xy\left( { - z} \right) + {z^3}}}{{3xyz}}\]
\[ = \frac{{ - {z^3} + 3xyz + {z^3}}}{{3xyz}} = \frac{{3xyz}}{{3xyz}} = 1.\]
Từ đó, \[T = \frac{{{a^3}{b^3} + {b^3}{c^3} + {c^3}{a^3}}}{{3{a^2}{b^2}{c^2}}} + \left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{c}{b}} \right) = 1 + \left( { - 1} \right) = 0.\]
Vậy \(T = 0.\)
−−−−−HẾT−−−−−
Đề thi học kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 2
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 8
Thời gian làm bài: phút
(Đề số 2)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Cho các biểu thức: x2 + y2; 2 025; có bao nhiêu đa thức?
A. 1.
B. 2.
C. 3.
D. 4.
Câu 2. Đẳng thức nào sau đây là hằng đẳng thức?
A. 3a + 1 = a + 3.
B. a + 3 = 3a - 1.
C. 2(a - 2) = 4a.
D. a(a + 1) = a2 + a.
Câu 3. Giá trị của x để phân thức có giá trị bằng 0 là
A. 1.
B. 2.
C. 3.
D. -1.
Câu 4. Hình chóp tam giác đều có mặt bên là hình gì?
A. Hình chữ nhật.
B. Hình vuông.
C. Hình tam giác.
D. Tam giác cân.
Câu 5. Hình dưới đây là một bóng đèn có 4 mặt bên là các tam giác cân, 1 mặt đáy là hình vuông.
Bóng đèn như vậy có dạng là hình gì?
A. Hình chóp tứ giác đều.
B. Hình chóp tam giác đều.
C. Hình chóp ngũ giác đều.
D. Không có tên gọi đặc biệt.
Câu 6. Cho hình chóp tứ giác đều có cạnh đáy dài 8 cm độ dài chiều cao 9 cm. Thể tích của hình chóp tứ giác đều đó là
A. 63 cm3.
B. 147 cm3.
C. 71 cm3.
D. 441 cm3.
Câu 7. Một chậu cây chóp tam giác đều có cạnh đáy 4 cm và trung đoạn hình chóp là 6 cm. Hỏi diện tích miếng bìa cần để bọc xung quanh một chậu cây là bao nhiêu? (không tính đến phần đường viền, nếp gấp).
A. 24 cm2.
B. 72 cm2.
C. 48 cm2.
D. 36 cm2.
Câu 8. Trong các phát biểu sau, phát biểu nào là định lý Pythagore?
A. Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
B. Nếu một tam giác có một cạnh bằng tổng của hai cạnh còn lại thì tam giác đó là tam giác vuông.
C. Nếu một tam giác có bình phương cạnh huyền bằng hiệu bình phương của hai cạnh góc vuông thì tam giác đó là tam giác vuông.
D. Trong một tam giác vuông, bình phương một cạnh bằng tổng bình phương của hai cạnh còn lại.
|
Câu 9. Số đo x trong hình vẽ bên là A. 83°. B. 93°. C. 103°. D. 113°. |
 |
Câu 10. Trong các hình sau, các hình nào có hai đường chéo vuông góc với nhau?
A. Hình chữ nhật, hình bình hành, hình thoi.
B. Hình bình hành, hình vuông, hình chữ nhật.
C. Hình thoi, hình vuông.
D. Hình thang cân, hình chữ nhật.
Câu 11. Cho bảng thống kê về tỉ số phần trăm các loại sách trong tủ sách của lớp 8A như sau:
|
Loại sách |
Tỉ số phần trăm |
|
Lịch sử Việt Nam |
25% |
|
Truyện tranh |
20% |
|
Thế giới động vật |
30% |
|
Các loại sách khác |
25% |
Cho các khẳng định sau:
(I) Dữ liệu định lượng là các loại sách: Lịch sử Việt Nam, Truyện tranh, thế giới động vật, các loại sách khác;
(II) Dữ liệu định tính là tỉ số phần trăm: 25%; 20%; 30%; 25%;
(III) Dữ liệu chưa hợp lí là tỉ số phần trăm.
Số khẳng định sai là
A. 0.
B. 1.
C. 2.
D. 3.
Câu 12. Để biểu diễn tỉ lệ của các phần trong tổng thể ta dùng biểu đồ nào sau đây?
A. Biểu đồ hình quạt tròn.
B. Biểu đồ đoạn thẳng.
C. Biểu đồ tranh.
D. Biểu đồ cột.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Thực hiện phép tính:
a) (6x - 7)(7x - 1);
b) ;
c) .
Bài 2. (1,0 điểm) Phân tích các đa thức sau thành nhân tử:
a) 3x3 + 6x2y + 3xy2;
b) x2 - 7x + 6.
Bài 3. (1,5 điểm) Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của Việt Nam qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng)
(Nguồn: Niên giám thống kê 2021)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
c) Tính tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại (làm tròn kết quả đến hàng phần mười).
Bài 4. (2,5 điểm)
|
1. Nhà bạn An (vị trí A trên hình vẽ) cách nhà bạn Châu (vị trí C trên hình vẽ) 600 m và cách nhà bạn Bình (vị trí B trên hình vẽ) 450 m. Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là ba đỉnh của một tam giác vuông (như hình vẽ). Tính khoảng cách từ nhà Bình đến nhà Châu. |
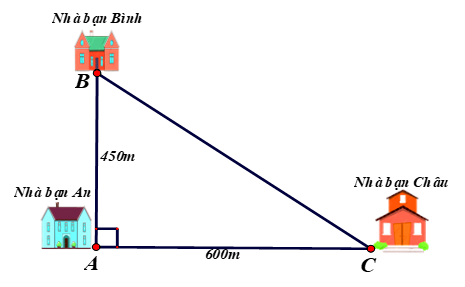 |
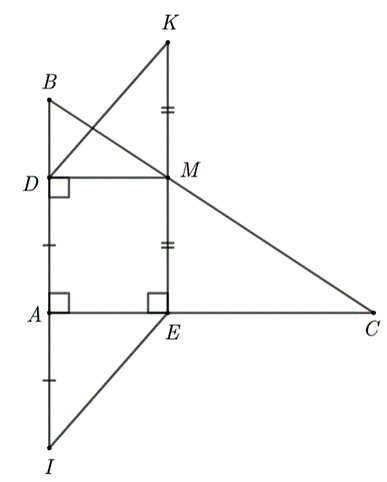
2. Cho tam giác ABC vuông tại A. Gọi M là một điểm bất kì trên cạnh huyền BC. Gọi D và E lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC.
a) Tứ giác ADME là hình gì? Vì sao?
b) Lấy điểm I sao cho A là trung điểm của ID; điểm K sao cho M là trung điểm của EK. Chứng minh EI = DK và EI // DK.
Bài 5. (0,5 điểm) Cho và a + b + c = 2022. Tính a, b, c.
−−−−−HẾT−−−−−
ĐÁP ÁN & HƯỚNG DẪN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
C |
D |
B |
D |
A |
B |
D |
A |
C |
C |
D |
A |
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm):
|
a) (6x - 7)(7x - 1) = = . |
b) = = . |
c)
=
= .
Bài 2. (1,0 điểm):
|
a)
|
b)
|
Bài 3. (1,5 điểm):
a) Biểu đồ đã cho là biểu đồ đoạn thẳng.
Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập gián tiếp bằng cách truy cập website của Niên giám thống kê 2021.
b) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2020 so với năm 2015 là: .
Vậy năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng khoảng 148,1% - 100% = 48,1% so năm 2015.
c) Tổng tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm 2015; 1017; 2018; 2019 là:
(nghìn tỉ đồng).
Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại (các năm 2015; 1017; 2018; 2019) là:
.
Vậy tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại khoảng 0,3%.
Bài 4. (2,5 điểm):
1. Trong hình vẽ trên, ta thấy tam giác ABC vuông tại A nên ta có:
BC2 = AB2 + AC2 (theo định lí Pythagore)
Suy ra .
Vậy khoảng cách từ nhà Bình đến nhà Châu là 750 m.
|
2. a) Xét tứ giác ADME có: (vì vuông tại A)
Do đó tứ giác ADME là hình chữ nhật. b) Vì ADME là hình chữ nhật nên AD = ME; AD // ME (tính chất hình chữ nhật). Mà A là trung điểm của DI; M là trung điểm của KE nên DI = KE; DI // KE. Suy ra DIKE là hình bình hành. Do đó DK // EI và DK = EI (đpcm). |
 |
Bài 5. (0,5 điểm):
Ta có
Ta thấy .
Khi đó, thì .
Khi đó a = b = c và a + b + c = 2022.
Do đó .
−−−−−HẾT−−−−−
Đề thi học kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 3
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán lớp 8
Thời gian làm bài: phút
(Đề số 3)
Câu 1 : Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Câu 2 : Tính giá trị của biểu thức: 302 + 452 - 252 + 60.45 được kết quả là
Câu 3 : Giá trị của biểu thức khi x = -2 là:
Câu 4 : Hiệu của biểu thức bằng:
Câu 5 : Cho . Đa thức P là:
Câu 6 : Cho ABCD là hình bình hành với các điều kiện như trên hình vẽ.
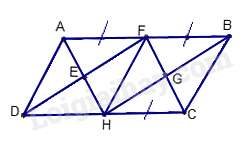
Trên hình này có:
Câu 7 : Tứ giác là hình chữ nhật nếu:
Câu 8 : Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích xung quanh của hình chóp.
Câu 9 : Cho hình chóp tam giác đều S.ABC có thể tích là 100 cm3; chiều cao của hình chóp là 3cm. Độ dài cạnh đáy của hình chóp đó là (Làm tròn đến hàng đơn vị)
Câu 10 : Độ dài một cạnh góc vuông và cạnh huyền của một tam giác vuông lần lượt là 3cm và 5cm. Diện tích của tam giác vuông đó là:
Câu 11 : Hình bình hành ABCD là hình chữ nhật khi:
Câu 12 : Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
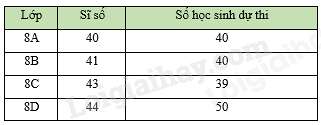
Câu 13 : Biểu đồ đoạn thẳng biểu diễn sô lượt người nước ngoài đến Việt Nam qua các năm 2018; 2019; 2020; 2021. (đơn vị: nghìn lượt người)
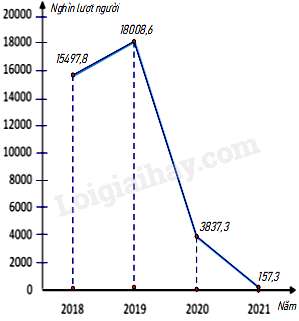
(Nguồn: Niên giám thống kê 2021)
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ đoạn thẳng ở hình bên ?
Số lượt người nước ngoài đến Việt Nam năm 2019 là bao nhiêu nghìn lượt người ?
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười) ?
Câu 1 : Cho phân thức:
a) Với điều kiện nào của x thì giá trị của phân thức A được xác định?
b) Rút gọn phân thức A.
c) Tính giá trị nguyên của x để phân thức A có giá trị nguyên.
Câu 2 : a) Tìm x, biết: x2 + 3x = 0
b) Tìm giá trị nhỏ nhất của biểu thức: x2 4x + 7
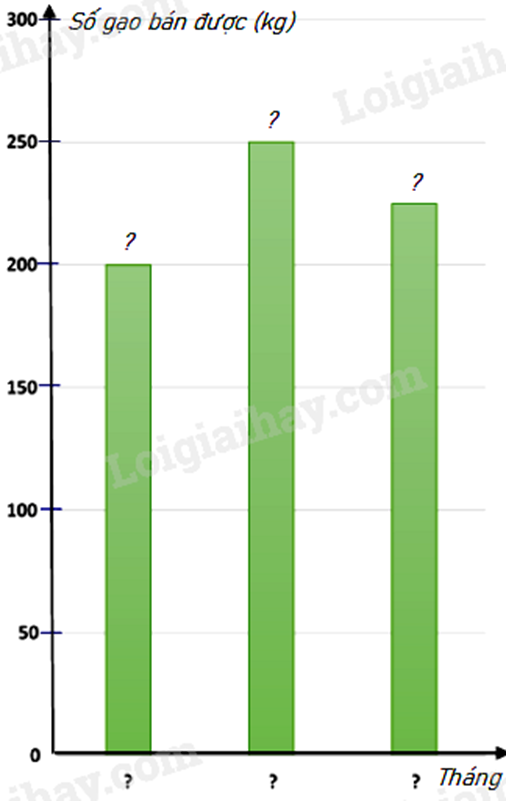
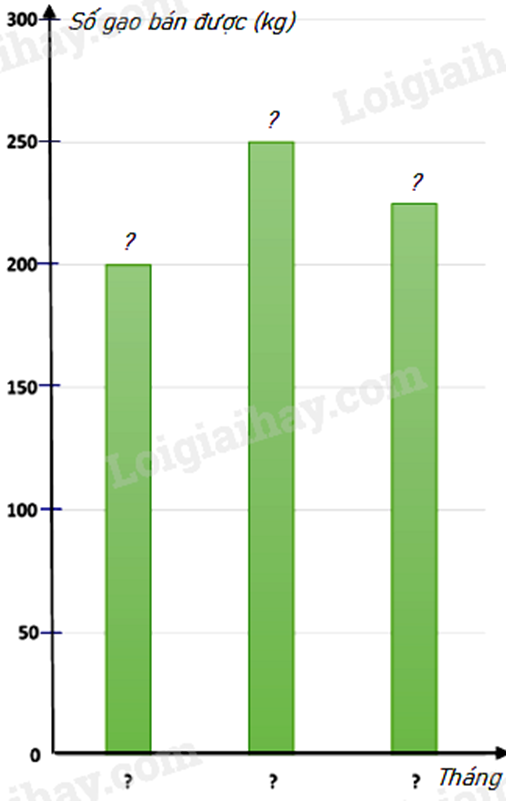
Câu 3 : Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2022.

a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2022 theo mẫu sau :

b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.
Câu 4 : 1. Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (Không tính phần viền xung quanh)
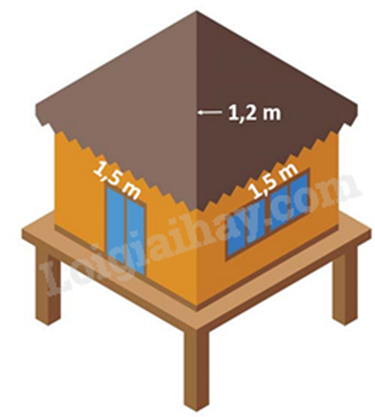
2. Cho tam giác vuông tại có . Gọi là trung điểm của , kẻ vuông góc với tại , vuông góc với tại .
a) Chứng minh .
b) Chứng minh tứ giác là hình bình hành.
c) Gọi là đường cao của tam giác (). Chứng minh tứ giác là hình thang cân.
Câu 5 : Tìm để biểu thức có giá trị là một số nguyên tố.
ĐÁP ÁN
| Câu 1-D | Câu 2-D | Câu 3-D | Câu 4-A | Câu 5-C | Câu 6-D | Câu 7-D |
| Câu 8-B | Câu 9-C | Câu 10-C | Câu 11-B | Câu 12-D | Câu 13- a) C; b) B; c) A |
Câu 1 :
a) Phân thức A xác định khi và chỉ khi
b) Ta có:
c) Phân thức A có giá trị nguyên khi và chỉ khi nguyên, hay .
Ta có bảng giá trị sau:
|
1 + 2x |
-1 |
1 |
|
x |
-1 (TM) |
0 (TM) |
|
|
-1 |
1 |
Vậy thì phân thức A có giá trị nguyên.
Câu 2 :
a)
Vậy x = 0 hoặc x = -3.
b) Ta có:
Vì với mọi nên với mọi .
Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức x2 4x + 7.
Vậy giá trị nhỏ nhất của x2 4x + 7 bằng 3 khi x – 2 = 0 hay x = 2.
Câu 3 :
a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2022 theo mẫu sau :

b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.
Câu 4 :
1.
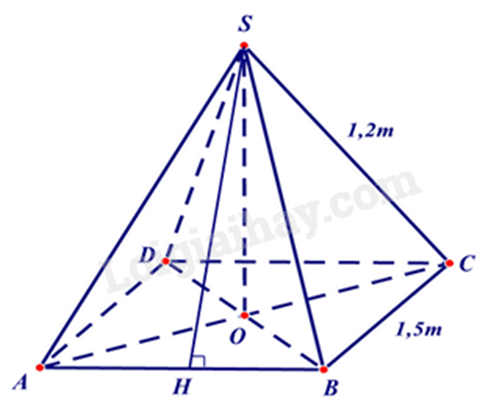
Ta có hình vẽ minh họa cho mái nhà của chòi như hình trên.
Gọi SH là đường cao của tam giác SAB nên SH là trung đoạn của hình chóp S.ABCD.
Vì S.ABCD là hình chóp tứ giác đều nên SAB là tam giác cân. Do đó SA = SB = 1,2m. Khi đó SH là đường cao đồng thời là đường trung tuyến nên AH = BH = AB = .1,5 = 0,75(m).
Áp dụng định lí Pythagore vào tam giác vuông SHB, ta có:
Diện tích vải bạc cần dùng để phủ mái chòi chính là diện tích xung quanh của hình chóp tứ giác đó.
Diện tích xung quanh của hình chóp là:
.
Vậy diện tích vải bạc cần dùng để phủ mái chòi là 3m2.
2.
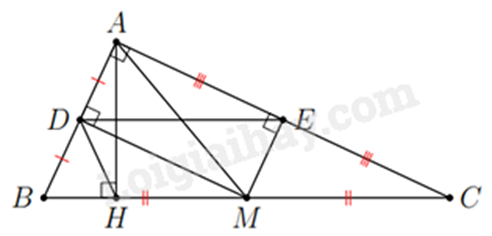
a) Xét tứ giác ADME có:
(tam giác ABC vuông tại A)
( vuông góc với tại , vuông góc với tại )
=> ADME là hình chữ nhật (tứ giác có 3 góc vuông).
b) Xét tam giác ABC vuông tại A có M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC nên AM = MC =
Khi đó tam giác AMC cân tại M. Mà ME vuông góc với AC nên ME là đường cao đồng thời là đường trung tuyến của tam giác AMC suy ra E là trung điểm của AC AE = EC. (1)
ADME là hình chữ nhật nên DM // AE và DM = AE (2)
Từ (1) và (2) suy ra DM // EC và DM = EC, do đó tứ giác DMCE là hình bình hành.
c) DMCE là hình bình hành nên DE // MC => DE // HM (H thuộc đường thẳng CM)
=> DHME là hình thang.
Xét tam giác AMB có AM = BM nên tam giác AMB cân tại M. Mà MD vuông góc với AB nên MD đường cao đồng thời là đường trung tuyến của tam giác ABM suy ra D là trung điểm của AB.
Xét tam giác ABH vuông tại H, D là trung điểm của AB nên HD là đường trung tuyến ứng với cạnh huyền của tam giác AHB => .
Mà ADME là hình chữ nhật nên AD = ME suy ra HD = ME.
Hình thang DHME có HD = ME nên DHME là hình thang cân.
Câu 5 :
Ta có:
Để A là số nguyên tố thì A chỉ có 2 ước là 1 và chính nó.
có ước là 1 và chính nó khi và chỉ khi hoặc .
Trường hợp 1. Với , ta có:
Khi đó
Trường hợp 2. Với , ta có:
(không thỏa mãn vì ).
Vậy n = 3 thì biểu thức có giá trị là một số nguyên tố.