Bộ 10 đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024

vietjack13 Ngày: 16-04-2024 Lớp 8

Mua tài liệu 3 K

Tailieumoi.vn xin giới thiệu bộ đề thi học kì 2 môn Toán lớp 8 sách Chân trời sáng tạo năm 2023 – 2024. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 2 Toán 8. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 8 Chân trời sáng tạo bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024

Đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Chân trời sáng tạo

Năm học 2023 - 2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Đường thẳng x = 2 luôn cắt trục hoành tại điểm

A. có hoành độ bằng 2, tung độ bằng 0.

B. có hoành độ bằng 0, tung độ bằng 2.

C. có hoành độ bằng 2, tung độ bằng 2.

D. có hoành độ bằng 2, tung độ tùy ý.

Câu 2. Cho hàm số y = $\frac{m - 1}{m + 1} x + 5$ . Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất?

A. m ≠ 1.

B. m ≠ -1.

C. m = 1.

D. m ≠ 1 và m ≠ -1.

Câu 3. Cho hàm số được xác định bởi công thức y = ax - 1. Biết đồ thị hàm số này đi qua điểm (1;2). Hoành độ của điểm thuộc đồ thị hàm số có tung độ bằng -4 là

A. -13.

B. -1.

C. -5.

D. -3.

Câu 4. Phương trình nào sau đây không là phương trình bậc nhất một ẩn?

A. 2x - 5 = 0.

B. $\frac{1}{x^{2}} + 1 = 0$ .

C. 4x - 3 = 0.

D. $\frac{1}{3} x + 2 = 0$ .

Câu 5. Phương trình x(x - 5) + 5x = 4 có bao nhiêu nghiệm?

A. 0.

B. 1.

C. 2.

D. Vô số nghiệm.

Câu 6. Cho hình vẽ dưới đây BC // ED. Độ dài EC là

A. EC = 2,78.

B. EC = 2,77.

C. EC = 2,75.

D. EC = 2,74.

10 Đề thi Học kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Câu 7. Đường trung bình của tam giác là đoạn thẳng đi qua

A. trung điểm của hai cạnh của một tam giác.

B. trung điểm của một cạnh của một tam giác.

C. hai đỉnh của một tam giác.

D. một đỉnh và một trung điểm của một cạnh của một tam giác.

Câu 8. Nếu $Δ A^{'} B^{'} C^{'} ∽ Δ A B C$ theo tỉ số đồng dạng k = $\frac{1}{2}$ thì

A. $\frac{A^{'} B^{'}}{A B} = \frac{1}{2}$ .

B. $\frac{A B}{A^{'} C^{'}} = 2$ .

C. $\frac{A^{'} B^{'}}{A C} = \frac{1}{2}$ .

D. $\frac{B C}{A^{'} B^{'}} = \frac{2}{1}$ .

Câu 9. Cho ∆ABC; ∆MNP nếu có $\hat{A} = \hat{M}$ , $\hat{B} = \hat{N}$ , $\hat{C} = \hat{P}$ để ∆ABC ᔕ ∆MNP theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?

A. $\frac{A B}{N P} = \frac{A C}{M P} = \frac{B C}{N M}$ .

B. $\frac{A B}{M P} = \frac{A C}{N P} = \frac{B C}{N M}$ .

C. $\frac{A B}{M N} = \frac{A C}{N P} = \frac{B C}{M P}$ .

D. $\frac{A B}{M N} = \frac{A C}{M P} = \frac{B C}{N P}$ .

Câu 10. Cho hình vẽ, biết ∆ABC ᔕ ∆MNP. Tỉ số $\frac{M N}{N P}$ bằng

10 Đề thi Học kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

A. $\frac{13}{5}$ .

B. $\frac{5}{13}$ .

C. $\frac{12}{5}$ .

D. .

Câu 11. Số kết quả có thể của hành động chọn ngẫu nhiên một chữ cái trong từ “MATHEMATIC” là

A. 10.

B. 7.

C. 9.

D. 8.

Câu 12. Bạn Nam tung một đồng xu cân đối và đồng chất 20 lần, có 13 lần mặt ngửa. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là

A. $\frac{13}{20}$ .

B. $\frac{7}{20}$ .

C. $\frac{13}{7}$ .

D. $\frac{7}{13}$ .

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm) Cho hàm số y = f(x) = $\frac{4}{x}$ .

a) Tính f(-4); f(8).

b) Hoàn thành bảng sau:

x	-2	?	2	3	?
y = f(x)	?	-4	?	?	8

Bài 2. (1,5 điểm) Đường sông từ A đến B ngắn hơn đường bộ là 10 km. Ca nô đi từ A đến B mất 2 giờ 20 phút, ô tô đi hết 2 giờ. Vận tốc ca nô nhỏ hơn vận tốc ô tô là 17km/h.

Bài 3. (1,0 điểm) Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.

a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?

b) Tính xác suất của mỗi biến cố “Số tự nhiên được viết ra là số tròn trăm”.

Bài 4. (1,0 điểm) Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?

10 Đề thi Học kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Bài 5. (2,5 điểm) Cho tam giác ABC có ba góc nhọn (AB < AC). Kẻ đường cao BE, AK và CF cắt nhau tại H.

a) Chứng minh: ∆ABK ᔕ ∆CBF.

b) Chứng minh: AE.AC = AF = AB.

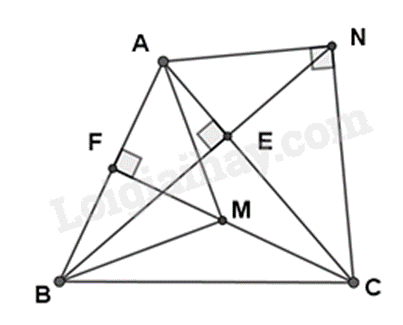
c) Gọi N là giao điểm của AK vàÈ, D là giao điểm của đường thẳng BC và đường thẳng EF và O, I lần lượt là trung điểm của BC vàAH. Chứng minh ON vuông góc DI.

−−−−−HẾT−−−−−

ĐÁP ÁN & HƯỚNG DẪN

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	A	D	B	B	C	C	A	A	D	D	B	B

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm)

a) Thay lần lượt các giá trị x = 4; x = 8 vào f(x), ta có:

y = f(-4) = $\frac{4}{- 4}$ = -1; f(8) = $\frac{4}{8} = \frac{1}{2}$ .

b) Ta điền các số còn thiếu vào bảng như sau:

x	-2	-1	2	3	$\frac{1}{2}$
y = f(x)	-2	-4	2	$\frac{4}{3}$	8

Bài 2. (1,5 điểm)

Gọi x (km/h) là vận tốc của ca nô (x > 0).

Vận tốc của ô tô là: x + 17 (km/h).

Quãng đường ca nô đi là: $\frac{10}{3} x (km)$ .

Quãng đường ô tô đi là 2(x + 17) (km).

Vì đường sông ngắn hơn đường bộ 10 km nên ta có phương trình:

$2 (x + 17) - \frac{10}{3} x = 10$

$2 x + 34 - \frac{10}{3} x = 10$

$\frac{10}{3} x - 2 x = 34 - 10$

$\frac{4}{3} x = 24$

x = 18 (thỏa mãn điều kiện).

Vậy vận tốc ca nô là 18 km/h. Vận tốc ô tô là 18 + 17 = 35 (km/h).

Bài 3. (1,0 điểm)

a) Các số tự nhiên có hai chữ số nhỏ hơn 200 là: {10;11;...;199}.

Vậy có 190 cách viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.

b) Có 9 kết quả thuận lợi cho biến cố“Số tự nhiên được viết ra là số tròn trăm” là 100;200;300;400;500;600;700;800;900.

Do đó, xác suất của biến cố “Số tự nhiên được viết ra là số tròn trăm” là: $\frac{9}{190}$ .

Bài 4. (1,0 điểm)

Vì Q là trung điểm EC, P là trung điểm của DC nên PQ là đường trung bình của tam giác CDE.

Khi đó $Q P = \frac{1}{2} D E$ .

Do đó DE = 2QP = 2.1,5 = 3 (m).

Vậy chiều dài mái DE bằng 3 m.

Bài 5. (2,5 điểm)

10 Đề thi Học kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Từ (3) và (4) nên suy ra FI = EI (6)

Từ (5) và (6) ta suy ra được OI là đường trung trực của cạnh EF.

Khi đó OI ⊥ EF hay OI ⊥ DN.

Do đó DN là đường cao của ∆DOI.

Xét ∆DOI có DN và IK là đường cao và N là giao của DN và IK.

Do đó N là trực tâm của tam giác DOI.

Vậy OI ⊥ DI (đpcm).

Đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Chân trời sáng tạo

Năm học 2023 - 2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề số 2)

I. Trắc nghiệm

Câu 1 : Trong các phương trình sau, phương trình bậc nhất một ẩn là

A.
$x^{2} - 1 = 0$ .
B.
$3 x + 2 = 0$ .
C.
$\frac{1}{x} - 3 x = 0$ .
D.
$\frac{2}{x - 3} = 0$ .

Câu 2 : Nghiệm của phương trình $4 (x - 1) - (x - 2) = - x$ là?

A.
$x = 2$ .
B.
$x = \frac{1}{2}$ .
C.
$x = 1$ .
D.
$x = - 1$ .

Câu 3 : Phương trình bậc nhất một ẩn $a x + b = 0 (a \neq 0)$ . Hạng tử tự do là

A.
a.
B.
b.
C.
0.
D.
x.

Câu 4 : Phương trình nào dưới đây chỉ có một nghiệm

A.
$4 x - 1 = 4 x + 3$ .
B.
$5 + 2 x = 2 x - 5$ .
C.
$3 x - 2 x = 3 x + 1$ .
D.
$x - 7 x = 1 - 6 x$ .

Câu 5 : Bạn An tung một đồng xu cân đối và đồng chất 20 lần, có 9 lần mặt ngửa, 11 lần mặt sấp. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là:

A.
$\frac{9}{11}$ .
B.
$\frac{11}{9}$ .
C.
$\frac{9}{20}$ .
D.
$\frac{11}{20}$ .

Câu 6 : Một hộp có 10 tấm thẻ cùng loại được đánh số từ 5 đến 14. Bạn An lấy ra ngẫu nhiên 1 thẻ từ hộp. Xác suất của biến cố “Chọn ra thẻ ghi số chia hết cho 5” là bao nhiêu phần trăm?

A.
20%.
B.
30%.
C.
40%.
D.
50%.

Câu 7 : Cho $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ . Khẳng định nào sau đây là sai?

A.
$\frac{A B}{A^{'} B^{'}} = \frac{A^{'} C^{'}}{A C} = \frac{B C}{B^{'} C^{'}}$ .
B.
$\frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C} = \frac{B^{'} C^{'}}{B C}$ .
C.
$\frac{B^{'} C^{'}}{B C} = \frac{A^{'} C^{'}}{A C} = \frac{A^{'} B^{'}}{A B}$ .
D.
$\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}}$ .

Câu 8 : Điều kiện để $Δ A B C ∽ Δ D E F$ theo trường hợp cạnh – góc – cạnh nếu $\hat{B} = \hat{E}$ là:

A.
$\frac{A B}{A C} = \frac{D E}{E F}$ .
B.
$\frac{A B}{D E} = \frac{B C}{E F}$ .
C.
$\frac{A B}{E F} = \frac{B C}{D E}$ .
D.
$\frac{A B}{D E} = \frac{A C}{D F}$ .

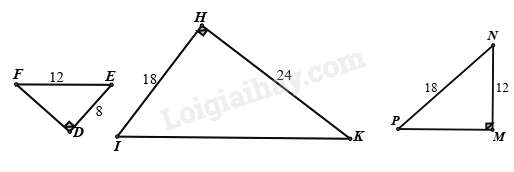
Câu 9 : Trong hình dưới đây, các tam giác nào đồng dạng với nhau là

Bộ 10 đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 1)

A.
$Δ D E F ∽ Δ H I K$ .
B.
$Δ D E F ∽ Δ M N P$ .
C.
$Δ H I K ∽ Δ M N P$ .
D.
Cả 3 tam giác đồng dạng.

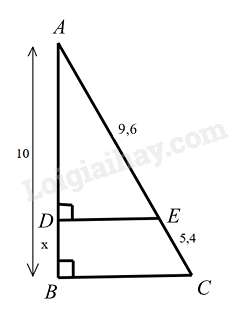
Câu 10 : Cho hình vẽ sau, giá trị của x là:

Bộ 10 đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 2)

A.
6,4.
B.
3,6.
C.
17,7.
D.
5,6.

Câu 11 : Trong các hình sau, cặp hình nào không phải luôn đồng dạng?

A.
Tam giác cân.
B.
Hình tròn.
C.
Tam giác đều.
D.
Hình vuông.

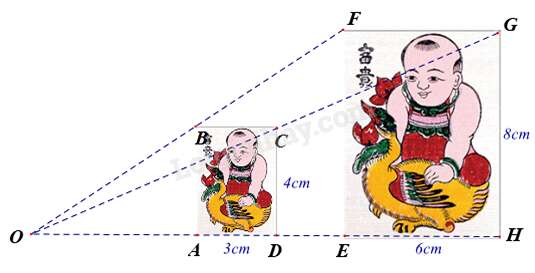
Câu 12 : Hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là

Bộ 10 đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 3)

A.
$k = \frac{1}{2}$ .
B.
$k = 1$ .
C.
$k = 2$ .
D.
$k = 4$ .

II. Tự luận

Câu 1 : Giải các phương trình sau:

a) $8 + 2 (x - 1) = 20$

b) $4 (3 x - 2) + 3 (x - 4) = 7 x + 20$

c) $\frac{2 x}{3} + x = \frac{2 x + 5}{6} + \frac{1}{2}$

Câu 2 : Giải bài toán bằng cách lập phương trình

Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 17 ngày. Do cải tiến kĩ thuật, năng suất mỗi ngày tăng thêm 7 tấm nên không những xí nghiệp đã hoàn thành kế hoạch sớm hơn 2 ngày mà còn dệt được thêm 7 tấm. Tính số thảm len mà xí nghiệp phải dệt theo hợp đồng.

Câu 3 : Cho $Δ A B C$ nhọn (AB < AC). Hai đường cao BE và CF.

a) Chứng minh $Δ A B E ∽ Δ A C F$ và $A E . A C = A F . A B$

b) Trên tia BE lấy điểm N sao cho $\hat{A N C} = 90^{0}$ (E nằm giữa B và N). Chứng minh $Δ A N E ∽ Δ A C N$ và $A N^{2} = A E . A C$ .

c) Trên cạnh CF lấy điểm M sao cho AM = AN. Tính số đo $\hat{A M B}$ .

Câu 4 : Số học sinh tham gia Câu lạc bộ Cờ tướng của một trường được biểu diễn ở biểu đồ sau:

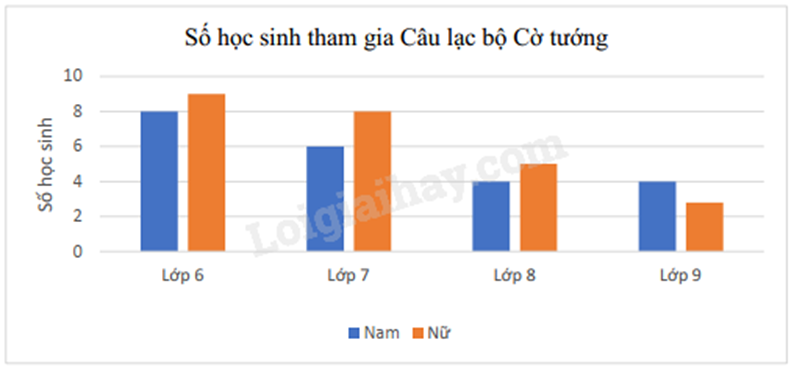
Bộ 10 đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 4)

Chọn ngẫu nhiên 1 học sinh Câu lạc bộ Cờ tướng của trường đó. Tính xác suất của biến cố “Học sinh được chọn là nam và không học lớp 7”.

Câu 5 : Giải phương trình $(3 x - 2) {(x + 1)}^{2} (3 x + 8) = - 16$ .

ĐÁP ÁN

I. Trắc nghiệm

Câu 1 :

Phương trình bậc nhất một ẩn là phương trình $3 x + 2 = 0$ .

Đáp án B.

Câu 2 :

$\begin{array}{l} 4 (x - 1) - (x - 2) = - x \\ 4 x - 4 - x + 2 = - x \\ 3 x - 2 = - x \\ 3 x + x = 2 \\ 4 x = 2 \\ x = \frac{1}{2} \end{array}$

Vậy $x = \frac{1}{2}$

Đáp án B.

Câu 3 :

Phương trình bậc nhất một ẩn $a x + b = 0 (a \neq 0)$ có hạng tử tự do là b.

Đáp án B.

Câu 4 :

Ta có:

$\begin{array}{l} 4 x - 1 = 4 x + 3 \\ 4 x - 4 x = 3 + 1 \end{array}$

$0 x = 4$ (vô lí)

Phương trình $4 x - 1 = 4 x + 3$ vô nghiệm

Giải tương tự, ta được:

Phương trình $5 + 2 x = 2 x - 5$ vô nghiệm;

Phương trình $3 x - 2 x = 3 x + 1$ có nghiệm duy nhất là $x = - \frac{1}{2}$ ;

Phương trình $x - 7 x = 1 - 6 x$ vô nghiệm.

Đáp án C.

Câu 5 :

Mặt sấp xuất hiện 11 lần nên xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là $\frac{11}{20}$ .

Đáp án D.

Câu 6 :

Các thẻ ghi số chia hết cho 5 là: 5; 10.

Có 2 kết quả thuận lợi cho biến cố “Chọn ra thẻ ghi số chia hết cho 5”.

Xác suất của biến cố “Chọn ra thẻ ghi số chia hết cho 5” là:

$\frac{2}{10} = 0, 2 = 20 %$

Đáp án A.

Câu 7 :

Vì $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ nên $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}}$ hay $\frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C} = \frac{B^{'} C^{'}}{B C}$ suy ra B, C, D đúng.

Đáp án A.

Câu 8 :

Để $Δ A B C ∽ Δ D E F$ theo trường hợp cạnh – góc – cạnh thì $\hat{B} = \hat{E}$ và $\frac{A B}{D E} = \frac{B C}{E F}$ .

Đáp án B.

Câu 9 :

Xét $Δ D E F$ và $Δ M N P$ có:

$\begin{array}{l} \hat{D} = \hat{M} = 90^{0} \\ \frac{D E}{M N} = \frac{E F}{N P} (\frac{8}{12} = \frac{12}{18} (= \frac{2}{3})) \end{array}$

nên $Δ D E F ∽ Δ M N P$ (cạnh huyền – cạnh góc vuông)

Áp dụng định lí Pythagore vào tam giác HIK có:

$K I = \sqrt{18^{2} + 24^{2}} = 30$

Vì $\frac{8}{12} = \frac{2}{3} \neq \frac{18}{30} = \frac{3}{5}$ nên $Δ D E F$ không đồng dạng với $Δ H I K$ .

Điều này dẫn đến $Δ M N P$ không đồng dạng với $Δ H I K$ (vì $Δ D E F ∽ Δ M N P$ )

Đáp án B.

Câu 10 :

Xét $Δ A B C$ và $Δ A D E$ có:

$\hat{B} = \hat{D} = 90^{0}$

$\hat{A}$ chung

Suy ra $Δ A B C ∽ Δ A D E$ (g.g)

Do đó $\frac{A B}{B C} = \frac{A D}{D E}$ hay $\frac{10}{9, 6 + 5, 4} = \frac{A D}{9, 6}$

Suy ra $A D = 9, 6. \frac{10}{9, 6 + 5, 4} = 6, 4$

Vậy $x = A B - A D = 10 - 6, 4 = 3, 6$ .

Đáp án B..

Câu 11 :

Tam giác cân không phải luôn đồng dạng.

Đáp án A.

Câu 12 :

Ta có: $\frac{3}{6} = \frac{4}{8} = \frac{1}{2}$ nên hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là $k = \frac{1}{2}$ .

Đáp án A.

II. Tự luận

Câu 1 :

a) $8 + 2 (x - 1) = 20$

$\begin{array}{l} 8 + 2 x - 2 = 20 \\ 2 x + 6 = 20 \\ 2 x = 20 - 6 \\ 2 x = 14 \\ x = 7 \end{array}$

Vậy $x = 7$

b) $4 (3 x - 2) + 3 (x - 4) = 7 x + 20$

$\begin{array}{l} 12 x - 8 + 3 x - 12 = 7 x + 20 \\ 12 x + 3 x - 7 x = 20 + 8 + 12 \\ 8 x = 40 \\ x = 5 \end{array}$

Vậy $x = 5$

c) $\frac{2 x}{3} + x = \frac{2 x + 5}{6} + \frac{1}{2}$

$\begin{array}{l} \frac{2.2 x}{6} + \frac{6 x}{6} = \frac{2 x + 5}{6} + \frac{3}{6} \\ 4 x + 6 x = 2 x + 5 + 3 \\ 10 x - 2 x = 8 \\ 8 x = 8 \\ x = 1 \end{array}$

Vậy $x = 1$

Câu 2 :

Gọi số thảm xí nghiệp phải dệt trong 1 ngày theo hợp đồng là x (tấm) (x > 0)

Thực tế một ngày xí nghiệp dệt được: x + 7 (tấm)

Số thảm len mà xí nghiệp phải dệt theo hợp đồng là: 17x (tấm)

Thực tế số thảm xí nghiệp dệt được là:

(17 – 2).(x + 7) = 15(x + 7) (tấm)

Theo bài ra ta có phương trình:

$15 (x + 7) = 17 x + 7$

Giải phương trình ta được: $x = 49$ (thỏa mãn)

Vậy số thảm len xí nghiệp phải dệt theo hợp đồng là: 17.49 = 833 (tấm)

Câu 3 :

Bộ 10 đề thi học kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 5)

a) Xét $Δ A B E$ và $Δ A C F$ có:

$\hat{A E B} = \hat{A F C} = 90^{0}$

$\hat{B A C}$ chung

Suy ra $Δ A B E ∽ Δ A C F$ (g.g). (đpcm)

Suy ra $\frac{A B}{A C} = \frac{A E}{A F}$ hay $A B . A F = A E . A C$ (đpcm) (1)

b) Xét $Δ A N E$ và $Δ A C N$ có:

$\hat{A E N} = \hat{A N C} = 90^{0}$

$\hat{N A C}$ chung

Suy ra $Δ A N E ∽ Δ A C N$ (g.g).

Suy ra $\frac{A N}{A C} = \frac{A E}{A N}$ hay $A N^{2} = A C . A E$ (đpcm). (2)

c) Từ (1) và (2) suy ra $A B . A F = A N^{2}$ .

Mà AM = AN (gt) suy ra $A M = A B . A F$ hay $\frac{A M}{A F} = \frac{A B}{A M}$ .

Xét $Δ A M F$ và $Δ A B M$ có:

$\hat{B A M}$ chung

$\frac{A M}{A F} = \frac{A B}{A M}$ (cmt)

Suy ra $Δ A M F ∽ Δ A B M (c . g . c)$

Suy ra $\hat{A M B} = \hat{A F M} = 90^{0}$ .

Câu 4 :

Số học sinh là nam và không học lớp 7 là:

8 + 4 + 4 = 16 (học sinh)

Có 16 kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và không học lớp 7”.

Tổng số kết quả có thể là:

8 + 9 + 6 + 8 + 4 + 5 + 4 + 3 = 47

Vậy xác suất của biến cố “Học sinh được chọn là nam và không học lớp 7” là: $\frac{16}{47}$ .

Câu 5 :

Nhân cả hai vế của phương trình $(3 x - 2) {(x + 1)}^{2} (3 x + 8) = - 16$ với 9, ta được:

$\begin{array}{l} 9. (3 x - 2) {(x + 1)}^{2} (3 x + 8) = - 16.9 \\ (3 x - 2) {[3 (x + 1)]}^{2} (3 x + 8) = - 144 \\ (3 x - 2) {(3 x + 3)}^{2} (3 x + 8) = - 144 \end{array}$

Đặt $3 x + 3 = t$ suy ra $3 x - 2 = t - 5$ ; $3 x + 8 = t + 5$

Ta được phương trình biến t như sau:

$(t - 5) t^{2} (t + 5) = - 144$

$\begin{array}{l} t^{4} - 25 t^{2} + 144 = 0 \\ (t^{2} - 9) (t^{2} - 16) = 0 \\ [\begin{array}{l} t^{2} = 9 \\ t^{2} = 16 \end{array} \\ [\begin{array}{l} t = \pm 3 \\ t = \pm 4 \end{array} \end{array}$