Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024

vietjack13 Ngày: 01-04-2024 Lớp 8

Mua tài liệu 4.6 K

Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 2 môn Toán lớp 8 sách Chân trời sáng tạo năm 2023 – 2024. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 2 Toán 8. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 2 Toán 8 Chân trời sáng tạo bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024

Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 2 - Chân trời sáng tạo

Năm học 2023 - 2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Cho hàm số $y = f (x) = 2 x^{2} - 1$ . Khẳng định nào sau đây là đúng?

A. f(-1) = -3.

B. f(1) = 1.

C. f(-1) = -1.

D. f(1) = 3.

Câu 2. Hàm số y = ax + b là hàm số bậc nhất khi

A. a = 0

B. a < 0

C. a > 0

D. a ≠ 0

Câu 3. Đồ thị của hai hàm số y = x + 2 và y = y + 1

A. cắt nhau.

B. trùng nhau.

C. song song với nhau.

D. Cả A, B, C đều sai.

Câu 4. Cho hình vẽ bên. Khẳng định nào sau đây là đúng về MN?

A. là đường trung tuyến của ∆ABC.

B. là đường trung bình của ∆ABC.

C. là đường trung trực của ∆ABC.

D. là đường phân giác của ∆ABC.

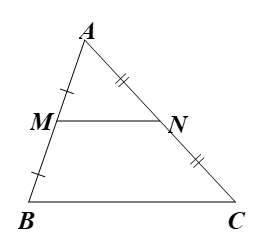10 Đề thi Giữa kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Câu 5. Cho hình vẽ bên, biết DE // AC. Tỉ số nào sau đây là đúng?

A. $\frac{B D}{A D} = \frac{B E}{E C}$ .

B. $\frac{B D}{A D} = \frac{B E}{B C}$ .

C. $\frac{D E}{A C} = \frac{B C}{B E}$

D. $\frac{A D}{A B} = \frac{B C}{E C}$ .

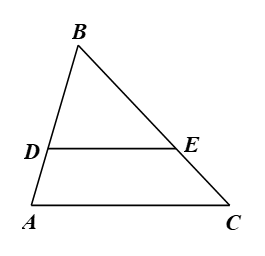Câu 6. Cho tam giác ABC có AB = 9 cm, AC = 6 cm. Vẽ AD là đường phân giác của góc A. Biết CD = 2 cm độ dài đoạn thẳng DB là

A. 1,5 cm

B. 3 cm

C. 4,5 cm

D. 6 cm

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Trong giờ thực hành thí nghiệm, một học sinh thả một miếng chì có khối lượng 0,31 kg đang ở nhiệt độ 100°C vào 0,25kg nước đang ở nhiệt độ 58,5°C. Biết nhiệt dung riêng của nước là 4 200 J/kg.K, nhiệt dung riêng của chì là 130 J/kg.K. gọi t°C là nhiệt độ khi đạt trạng thái cân bằng nhiệt, Q_nuoc (J) là nhiệt lượng nước thu vào để tăng nhiệt độ từ 58,5°C lên t°C, Q_nuoc (J) là nhiệt lượng chì tỏa ra để giảm nhiệt độ từ 100°C xuống t°C.

a) Biết công thức tính nhiệt lượng thu vào/ tỏa ra là: Q = m.c.∆t (J), trong đó m là khối lượng của vật (kg), c là nhiệt dung riêng của chất làm nên vật (J/kg.K) và ∆t = t₂ - t₁ là độ tăng/giảm nhiệt độ của vật (°C) với t₁ là nhiệt độ ban đầu, t₂ là nhiệt độ cuối cùng. Viết công thức tính Q_chi và Q_nuoc theo t.

b) Khi có sự cân bằng nhiệt thì nhiệt độ của nước và chì là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Bài 2. (2,5 điểm) Cho hàm số y = (m - 1)x + m (m là tham số m ≠ 1) có đồ thị là đường thẳng (d).

a) Tìm m để (d): y = (m - 1)x + m song song với (d'): y = 2x - 3.

b) Vẽ (d) với m tìm được và vẽ (d') trên cùng mặt phẳng tọa độ Oxy.

c) Tìm m để đường thẳng (d): y = (m - 1)x + m và hai đường thẳng $y = x + 2; y = \frac{1}{2} x + 3$ đồng quy.

Bài 3. (3,0 điểm)

1) Cho tam giác ABC có BC = 15 cm, CA = 18 cm và AB = 12 cm. Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm ∆ABC.

a) Tính độ dài các đoạn thẳng CD và BD.

b) Chứng minh IG // BC.

c) Tính độ dài đoạn thẳng IG.

2) Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố bên ngoài tác động vào (Hình a).

10 Đề thi Giữa kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Hình a

10 Đề thi Giữa kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Hình b

Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài x của cây chống đứng bên và độ dài y của cánh kèo.

-----HẾT-----

ĐÁP ÁN & HƯỚNG DẪN

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5	6
Đáp án	B	D	C	B	A	B

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Nhiệt lượng chì tỏa ra để giảm nhiệt độ từ 100°C xuống t°C là:

Q_chi = 0,31.130.(100 - t) = -40,3t + 4 030 (J).

Nhiệt lượng nước thu vào để tăng nhiệt độ từ 58,5°C lên t°C là:

Q_nuoc = 0,25.4 200.(t - 58,5) = 1 050t - 61 425 (J).

b) Khi cân bằng nhiệt, nhiệt lượng tỏa ra bằng với nhiệt lượng thu vào nên ta có"

Q_nuoc = Q_chi

Do đó 1 050t - 61 425 = -40,3t + 4 030

1 090,3t = 65 455

t ≈ 60

Vậy nhiệt độ của nước và chì khi đạt trạng thái cân bằng nhiệt là khoảng 60°C.

Bài 2. (2,5 điểm)

a) Với m ≠ 1 để đường thẳng (d): y = (m - 1)x + m song song với đường thẳng (d'): y = 2x - 3 thì m- 1 = 2 và m ≠ -3 tức là m = 3 (thỏa mãn m ≠ 1, m ≠ -3).

Vậy m = 3.

b) ⦁ Với m = 3 ta có hàm số y = 2x + 3.

Cho x = 0 ta có y = 3.

Cho x = -1 ta có y = 1.

Đồ thị hàm số y = 2x + 3 là đường thẳng (d) đi qua hai điểm (0; 3) và (-1; 1).

⦁ Xét hàm số y = 2x - 3

Cho x = 0 ta có y = -3.

Cho x = 1 ta có y = -1.

Đồ thị hàm số y = 2x - 3 là đường thẳng (d') đi qua hai điểm (0; -3) và (1; -1).

10 Đề thi Giữa kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

c) Gọi $A (x_{A}; y_{A})$ là giao điểm của hai đường thẳng $y = x + 2; y = \frac{1}{2} x + 3$ .

Vì A thuộc đường thẳng y = x + 2 nên ta có $y_{A} = x_{A} + 2$ . Khi đó $A (x_{A}; x_{A} + 2)$ .

Vì A thuộc đường thẳng $y = \frac{1}{2} x + 3$ nên ta có $x_{A} + 2 = \frac{1}{2} x_{A} + 3$ , suy ra $\frac{1}{2} x_{A} = 1$ , do đó x_A = 2.

Từ đó ta có $y_{A} = x_{A} + 2 = 2 + 2 = 4$ .

Vì vậy ta được A(2;4).

Để ba đường thẳng $y = x + 2; y = \frac{1}{2} x + 3$ và $(d) : y = (m - 1) x + m$ đồng quy thì đường thẳng (d) phải đi qua giao điểm A(2;4) của hai đường thẳng $y = x + 2; y = \frac{1}{2} x + 3$ .

Khi đó x = 2, y = 4 thỏa mãn hàm số y = (m - 1)x + m, ta được:

$4 = (m - 1) \cdot 2 + m$ , suy ra $2 m - 2 + m = 4$ , do đó 3m = 6 nên m = 2 (thỏa mãn m ≠ 1).

Vậy m = 2.

Bài 3. (3,0 điểm)

10 Đề thi Giữa kì 2 Toán 8 Chân trời sáng tạo (có đáp án + ma trận)

Đặt các điểm $A, B, C, D, E, M, N, P$ như hình vẽ trên.

⦁ Xét ∆AMC có E, P lần lượt là trung điểm của AC, MC (do EA = EC, PM = PC) nên EP là đường trung bình của ∆AMC.

Do đó $E P = \frac{1}{2} A M = \frac{1}{2} \cdot 2,7 = 1,35 (m)$ (tính chất đường trung bình của tam giác).

Hay x = 1,35 (m).

⦁ Ta có MB = MN + NB và MC = MP + PC

Mà MN = NB = MP = PC nên MB = MC

Xét ∆ABC có D, M lần lượt là trung điểm của AB, BC (do DB = DA, MB = MC nên DM là đường trung bình của ∆ABC.

Do đó $D M = \frac{1}{2} A C$ (tính chất đường trung bình của tam giác).

Suy ra AC= 2DM = 2.2,8 = 5,6 (m). Hay y = 5,6 (m).

Vậy độ dài của cây chống đứng bên và độ dài của của cánh kèo lần lượt là x = 1,35 (m); y = 5,6 (m).

Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 2 - Chân trời sáng tạo

Năm học 2023 - 2024

Môn: Toán lớp 8

Thời gian làm bài: phút

(Đề số 2)

I. Trắc nghiệm

Câu 1 : Cho hàm số $y = f (x) = x^{2} .$ Tính $f (- 5) + f (5)$ .

A
0.
B
25.
C
50.
D
10.

Câu 2 : Thanh long là một loại cây chịu hạn , không kén đất, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (kg) thanh long ruột đỏ loại I là :

A
y = 32 000.
B
y = 32 000 – x.
C
y = 32 000x.
D
y = 32 000 + x.

Câu 3 : Màn hình ra đa của một đài gợi lên hình ảnh một mặt phẳng tọa độ. Ba chấm sáng trên màn hình ra đa của đài nằm ở góc phần tư thứ mấy trong mặt phẳng tọa độ Oxy ?

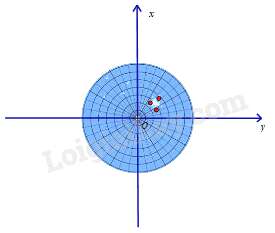
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 1)

A
Góc phần tư thứ I.
B
Góc phần tư thứ II.
C
Góc phần tư thứ III.
D
Góc phần tư thứ IV.

Câu 4 : Trong mặt phẳng tọa độ Oxy như hình vẽ. Câu trả lời nào sau đây không đúng ?

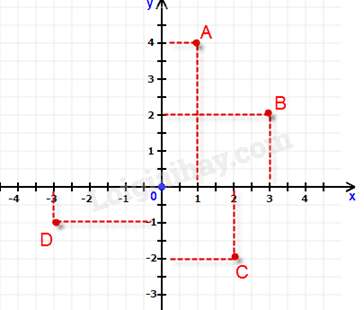
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 2)

A
A(1; 4).
B
B(3; 2).
C
C(2;-2).
D
D(-3;-1).

Câu 5 : Hàm số nào sau đây là hàm số bậc nhất?

A
$y = 2 x - 1$ .
B
$y = - x^{2} + 3$ .
C
$y = \frac{1}{x}$ .
D
$y = 2024$ .

Câu 6 : Hệ số góc của hàm số $y = - x - 3$ là:

A
1.
B
-1.
C
3.
D
-3.

Câu 7 : Viết tỉ số cặp đoạn thằng có độ dài như sau: AB = 4dm; CD = 20dm.

A
$\frac{A B}{C D} = \frac{1}{4}$ .
B
$\frac{A B}{C D} = \frac{1}{5}$ .
C
$\frac{A B}{C D} = \frac{1}{6}$ .
D
$\frac{A B}{C D} = \frac{1}{7}$ .

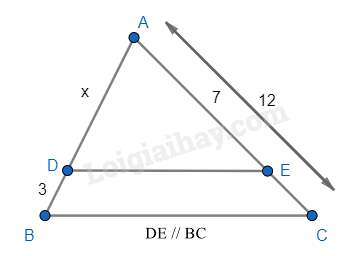
Câu 8 : Tìm giá trị của x trong hình vẽ?

Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 3)

A
$x = \frac{21}{5}$ .
B
$x = 2, 5$ .
C
$x = 7$ .
D
$x = \frac{21}{4}$ .

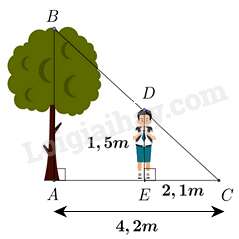
Câu 9 : Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.

Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 4)

A
$A B = 3 m$ .
B
$A B = 0, 75 m$ .
C
$A B = 2, 4 m$ .
D
$A B = 2, 25 m$ .

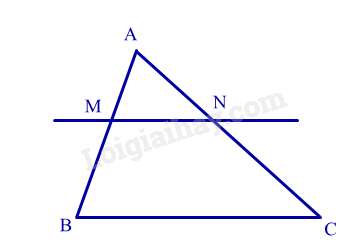
Câu 10 : Cho hình vẽ sau. Biết MN // BC, AM = 2cm, BM = 3cm, AN = 3cm. Độ dài đoạn thẳng NC bằng:

Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 5)

A
3cm.
B
4,5cm.
C
2,5cm.
D
4cm.

Câu 11 : Cho tam giác ABC có P, Q lần lượt là trung điểm của AB và AC. Biết BC = 10cm. Ta có:

A
PQ = 4cm.
B
PQ = 5cm.
C
PQ = 3,5cm.
D
PQ = 10cm.

Câu 12 : Cho $Δ A B C$ , AD là tia phân giác trong của góc A. Hãy chọn câu đúng.

A
$\frac{D C}{D B} = \frac{A B}{A C}$ .
B
$\frac{A B}{D B} = \frac{A C}{D C}$ .
C
$\frac{A B}{D B} = \frac{D C}{A C}$ .
D
$\frac{A D}{D B} = \frac{A C}{A D}$ .

II. Tự luận

Câu 1 : Cho hàm số $y = - 2 x + 1$ (1).

a) Chứng minh các điểm $A (0; 1)$ và $B (\frac{3}{2}; - 2)$ thuộc đồ thị của hàm số (1) trong mặt phẳng tọa độ Oxy.

b) Biểu diễn A và B trong mặt phẳng tọa độ Oxy.

c) Tìm tọa độ điểm C nằm trên trục hoành và thuộc đồ thị của hàm số (1) trong mặt phẳng tọa độ Oxy.

Câu 2 : Học sinh khối 8 ở một trường góp tiền để làm một album ca nhạc Tết Nguyên Đán 2024. Một phòng thu âm cho biết giá sản xuất đĩa gốc là 10 triệu đồng và mỗi đĩa in sao là 60 000 đồng.

a) Gọi x là số đĩa cần in sao và y là số tiền học sinh khối 8 phải trả (bao gồm tiền đĩa in sao và một đĩa gốc). Hãy biểu diễn y theo x. Hỏi y có phải là hàm số bậc nhất không? Vì sao?

b) Các bạn khối 8 cần góp bao nhiêu tiền để in được 150 đĩa sao và một đĩa gốc?

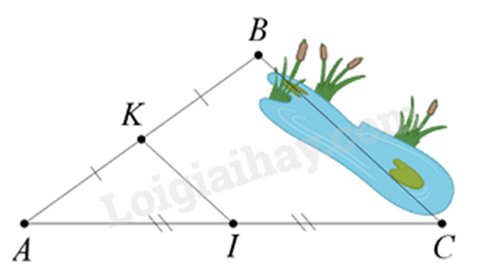
Câu 3 : Giữa hai điểm $B$ và $C$ bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài $B C$ mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng $K I$ dài $30 m$ và $K$ là trung điểm của $A B$ , $I$ là trung điểm của $A C$ .

Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 6)

Câu 4 : Cho tam giác ABC vuông tại A. Gọi O là trung điểm của AC. Trên tia BO lấy điểm D sao cho O là trung điểm của BD.

a) Chứng minh tứ giác ABCD là hình bình hành.

b) Trên tia BA lấy điểm E sao cho A là trung điểm của BE. Chứng minh rằng AC = ED.

c) Qua O kẻ OM, ON lần lượt là phân giác của các góc BOA và BOC ( $M \in A B, N \in B C$ ).

Chứng minh rằng MN // AC và BO đi qua trung điểm của MN.

Câu 5 : Cho đường thẳng d: y = mx + m – 1. Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho tam giác AOB vuông cân.

ĐÁP ÁN

I. Trắc nghiệm

Câu 1 : Đáp án : C

Câu 2 : Đáp án : C

Câu 3 : Đáp án : A

Câu 4 : Đáp án : D

Câu 5 : Đáp án : A

Câu 6 : Đáp án : B

Câu 7 : Đáp án : B

Câu 8 : Đáp án : A

Câu 9 : Đáp án : A

Câu 10 : Đáp án : B

Câu 11 : Đáp án : B

Câu 12 : Đáp án : B

II. Tự luận

Câu 1 :

a) Ta có: $- 2.0 + 1 = 1 \Rightarrow A (0; 1)$ thuộc đồ thị của hàm số (1) (đpcm)

$- 2. \frac{3}{2} + 1 = - 3 + 1 = - 2 \Rightarrow B (\frac{3}{2}; - 2)$ thuộc đồ thị của hàm số (1) (đpcm).

b) Biểu diễn A trong mặt phẳng tọa độ Oxy:

- Điểm A có hoành độ bằng 0 nên nằm trên trục tung.

- Trên trục tung lấy điểm 1 ta được điểm $A (0; 1)$ .

Biểu diễn B trong mặt phẳng tọa độ Oxy.

- Trên trục hoành lấy điểm $\frac{3}{2}$ , vẽ đường thẳng vuông góc với trục hoành tại điểm $\frac{3}{2}$ .

- Trên trục tung lấy điểm $- 2$ , vẽ đường thẳng vuông góc với trục tung tại điểm $- 2$ .

- Giao điểm của hai đường thẳng vừa vẽ là điểm B cần tìm.

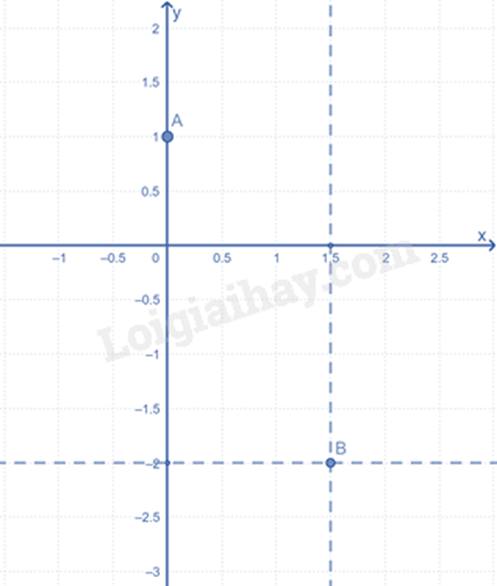
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 7)

c) Điểm C nằm trên trục hoành nên có tung độ bằng 0.

Điểm C thuộc đồ thị của hàm số (1) nên ta có:

$\begin{array}{l} - 2 x_{C} + 1 = 0 \\ x_{C} = \frac{1}{2} \end{array}$

Vậy tọa độ điểm C là $C (\frac{1}{2}; 0)$ .

Câu 2 :

a) Số tiền in đĩa gốc là 10 triệu đồng và số tiền in mỗi đĩa in sao là 60 000 nên nếu in x đĩa in sao và một đĩa gốc thì số tiền là: y = 60 000.x + 10 000 000

Vì hàm số y có dạng y = ax + b với a = 60 000 $\neq$ 0 nên y là hàm số bậc nhất.

b) Để in được 150 đĩa sao và một đĩa gốc thì các bạn khối 8 cần góp số tiền là:

y = 60 000.150 + 10 000 000 = 19 000 000 (đồng)

Vậy các bạn khối 8 cần góp 19 000 000 đồng để in được 150 đĩa sao và một đĩa gốc.

Câu 3 :

Vì K là trung điểm của AB, I là trung điểm của AC nên KI là đường trung bình của tam giác ABC

=> KI // BC và KI = $\frac{1}{2}$ BC.

Vì KI = 30 m nên BC = 2.KI = 2.30 = 60 m.

Vậy BC = 60 m.

Câu 4 :

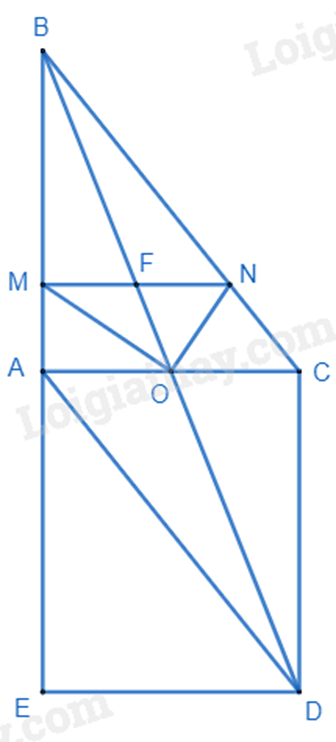
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án năm 2024 (ảnh 8)

a) Xét tứ giác ABCD có:

O là trung điểm của AC

O là trung điểm của BD.

$A C \cap B D = O$

$\Rightarrow$ ABCD là hình bình hành. (đpcm)

b) Xét tam giác BED có:

A là trung điểm của BE

O là trung điểm của BD

$\Rightarrow$ AO là đường trung bình của tam giác BED.

$\Rightarrow A O = \frac{1}{2} E D$

Mà $A O = \frac{1}{2} A C$ (O là trung điểm của AC)

$\Rightarrow A C = E D$ (đpcm)

c) Áp dụng tính chất của đường phân giác, ta có:

OM là tia phân giác của $\hat{A O B}$ $\Rightarrow \frac{A O}{A M} = \frac{O B}{B M} \Rightarrow \frac{A O}{O B} = \frac{A M}{B M}$

ON là tia phân giác của $\hat{B O C}$ $\Rightarrow \frac{O C}{C N} = \frac{O B}{B N} \Rightarrow \frac{O C}{O B} = \frac{C N}{B N}$

Mà $A O = O C$ (gt)

$\Rightarrow \frac{A M}{B M} = \frac{C N}{B N}$ $\Rightarrow M N / / A C$ (định lí Thales đảo) (đpcm)

Gọi F là giao điểm của MN và BO.

Vì MN // AC nên áp dụng hệ quả của định lí Thales vào:

$Δ A O B$ có: $\frac{B F}{B O} = \frac{M F}{A O}$

$Δ B O C$ có: $\frac{B F}{B O} = \frac{N F}{O C}$

$\Rightarrow \frac{M F}{A O} = \frac{N F}{O C} \Rightarrow \frac{M F}{N F} = \frac{A O}{O C} = 1 \Rightarrow M F = N F$ hay F là trung điểm của MN $\Rightarrow$ BO đi qua trung điểm của MN. (đpcm)

Câu 5 :

Ta có: $d \cap O y = {B}$

$x_{B} = 0 \Rightarrow y_{B} = m - 1$ $\Rightarrow B (0; m - 1)$ $\Rightarrow O B = | m - 1 |$ .

$y_{A} = 0 \Leftrightarrow m x_{A} + m - 1 = 0 \Leftrightarrow x_{A} = \frac{1 - m}{m} (m \neq 0)$ $\Rightarrow A (\frac{1 - m}{m}; 0)$ $\Rightarrow O A = | \frac{1 - m}{m} |$ .

Vì tam giác AOB vuông cân tại O nên:

$\begin{array}{l} O A = O B \\ | m - 1 | = | \frac{1 - m}{m} | \\ [\begin{array}{l} m - 1 = \frac{1 - m}{m} \\ m - 1 = - \frac{1 - m}{m} \end{array} \\ [\begin{array}{l} m^{2} = 1 \\ (m - 1) (1 - \frac{1}{m}) = 0 \end{array} \\ [\begin{array}{l} m = \pm 1 \\ m = 1 \end{array} \\ m = \pm 1 (T M) \end{array}$