Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bồi dưỡng và phát triển tư duy đột phá Toán 8 (Tập 2 - Hình học), tài liệu bao gồm 199 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu gồm có

I. Lý thuyết.

II. Luyện kỹ năng giải bài tập.

Chương I. Tứ giác

Bài 1. Tứ giác

A. Lý thuyết

1) Định nghĩa:

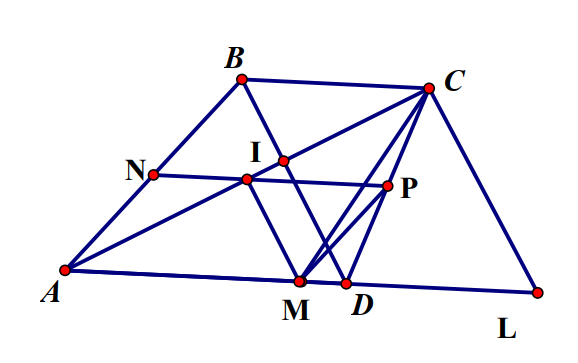
Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA, trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bát kỳ cạnh nào của tứ giác.

Hai đỉnh kề nhau: A và B; B và C; C và D; D và A

Hai đỉnh đối nhau: A và C; B và D

Đường chéo AC; BD

Hai cạnh kề nhau: AB và BC; BC và CD; CD và DA

Hai cạnh đối nhau: AB và CD; AD và BC

Hai góc kề nhau: \(\widehat A\) và \(\widehat B\); \(\widehat B\) và \(\widehat C\);\(\widehat C\) và \(\widehat D\); \(\widehat D\) và \(\widehat A\)

Hai góc đối nhau: \(\widehat A\) và \(\widehat C\); \(\widehat B\) và \(\widehat D\)

Điểm nằm trong tứ giác: M

Điểm nằm trên tứ giác: N

Điểm nằm ngoài tứ giác: P

2) Định lý: Tổng các góc của một tứ giác bằng 180^o

B. Luyện kĩ năng giải bài tập

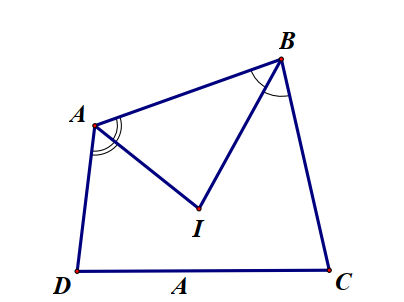
Bài 1. Cho tứ giác ABCD biết \(\widehat B\) + \(\widehat C\) = 200^o, \(\widehat B\) + \(\widehat D\) = 180^o, \(\widehat C\) + \(\widehat D\) = 120^o.

a) Tính số đo các góc của tứ giác.

b) Gọi I là giao điểm của các tia phân giác của \(\widehat A\) và \(\widehat B\) của tứ giác. Chứng minh: \(\widehat {AIB} = \frac{{\widehat C + \widehat D}}{2}\)

Bài giải

a) Từ giả thiết ta có:

 \(\begin{array}{l}2\widehat B + 2\widehat C + 2\widehat D = {200^O} + {180^O} + {120^O}\\ \Rightarrow \widehat B + \widehat C + \widehat D = {250^O}.\end{array}\)

Vì \(\)\(\widehat A + \widehat B + \widehat C + \widehat D = {360^O} \Rightarrow \widehat A = {110^O}\)

\(\widehat B = {250^O} - \left( {\widehat C + \widehat D} \right) = {250^O} - {120^O} = {130^O}\)

\(\widehat C = {200^O} - \widehat B = {200^O} - {130^O} = {70^O}\)

\(\widehat D = {120^O} - \widehat C = {120^O} - {70^O} = {50^O}\)

b) Trong tam giác ABI:

\(\widehat {AIB} = {180^O} - \frac{{\widehat A + \widehat B}}{2} = \frac{{{{360}^O} - \left( {\widehat A + \widehat B} \right)}}{2} = \frac{{\widehat C + \widehat D}}{2}.\)

Bài 2. Cho tứ giác lồi ABCD có \(\widehat B + \widehat D = {180^O},\,\,CB = CD\). Chứng minh AC là tia phân giác của \(\widehat {BAD}\).

Bài giải

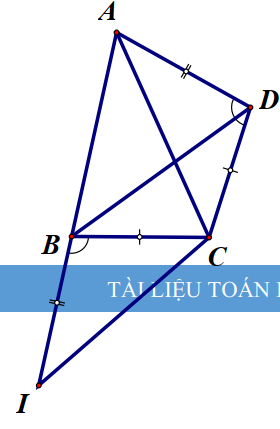
Trên tia đối ta BA lấy điểm I sao cho BI = AD.

Ta có \(\widehat {ADC} = \widehat {IBC}\) (cùng bù với góc \(\widehat {ABC}\))

AD = IB, DC = BC. Từ đó ta có

Suy ra: \(\widehat {DAC} = \widehat {BIC}\) và AC = IC.

Tam giác ACI cân tại C nên \(\widehat {BAC} = \widehat {BIC} = \widehat {DAC}.\)

Vậy AC là phân giác trong góc \(\widehat {BAD}.\)

Bài 3. Cho tứ giác lồi ABCD, hai cạnh của AD và BC cắt nhau tại E, hai cạnh DC và AB cắt nhau tại F. Kẻ tia phân giác của hai góc CED và BFC cắt nhau tại I. Tính góc EIF theo các góc trong tứ giác ABCD.

Bài giải:

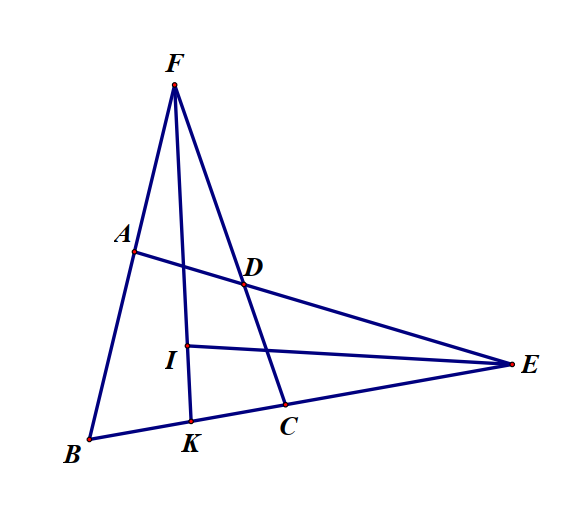
FI cắt BC tại K, suy ra K thuộc đoạn BC

\( \Rightarrow \widehat {EIF} = \widehat {EIK} + \widehat {IEK}\,\,(\widehat {EIF}\)là góc ngoài của

\( = \widehat B + \widehat {BFK} + \widehat {IEK}\,\,(\widehat {CKF}\) là góc ngoài của

\(\begin{array}{l}\widehat {BFC} = {180^O} - \left( {\widehat B + \widehat C} \right)\\ \Rightarrow \widehat {BFK} = {90^O} - \frac{{\widehat B + \widehat C}}{2}\end{array}\)

\(\begin{array}{l}\widehat {AEB} = {180^O} - \left( {\widehat A + \widehat B} \right)\\ \Rightarrow \widehat {IEK} = {90^O} - \frac{{\widehat A + \widehat B}}{2}.\end{array}\)

Vậy \(\widehat {EIF} = \widehat B + {90^O} - \frac{{\widehat B + \widehat C}}{2} + {90^O} - \frac{{\widehat A + \widehat B}}{2}\)

\( = {180^O} - \frac{{\widehat A + \widehat C}}{2} = \frac{{\widehat B + \widehat D}}{2}\)

Bài 4. Cho tứ giác ABCD. Chứng minh: \(\frac{1}{2}\)p < AC + BD < p (p: chu vi của tứ giác)

Bài giải:

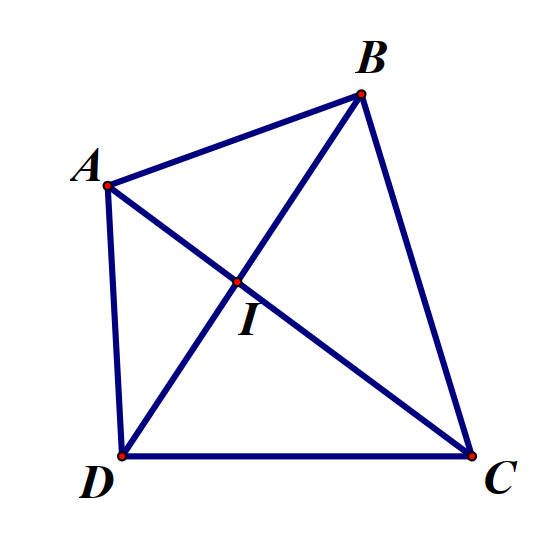
Gọi I là giao điểm của AC và BD. Theo bất đẳng thức tam giác, ta có:

IA + IB > AB, IA + ID > AD, IB + IC > BC, IC + ID > CD

Cộng theo vế, ta được: 2(IA + IB + IC + ID) > p, từ đó:

AC + BD > \(\frac{1}{2}\)p.

Lại có: AC < AB + BC, AC < AD + DC,

BD < BA + AD, BD < BC + CD.

Suy ra 2(AC + BD) < 2(AB + BC + CD + DA) = 2p

=> AC + BD < p.

Bài 5. Cho tứ giác ABCD, M là một điểm trong tứ giác đó. Xác định vị trí của M để MA + MB + MC + MD nhỏ nhất.

Bài giải:

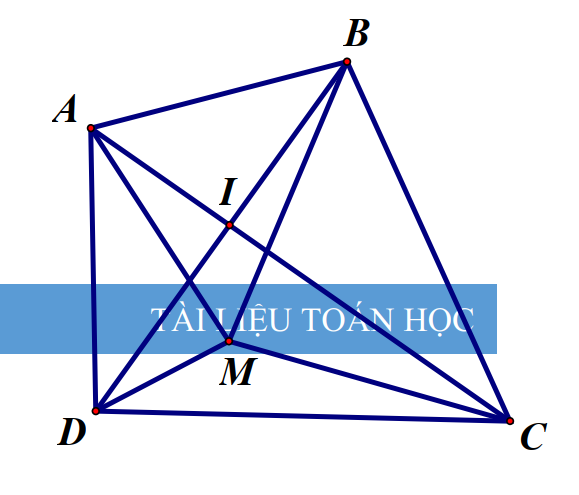
Gọi I là giao điểm của AC và BD. Ta có các bất đẳng thức:

MA + MC \( \ge \) AC, MB + MD \( \ge \)BD.

MA + MB + MC + MD = AC + BD khi M trùng với I.

Vậy khi M là giao điểm của hai đường chéo thì MA + MB + MC + MD nhỏ nhất.

Bài 6: Một đường thẳng đi qua trung điểm của hai cạnh đối điện của một tứ giác lòi tạo với các đường chéo của hai góc bằng nhau. Chứng minh rằng tứ giác ấy có hai đường chéo bằng nhau.

Bài giải:

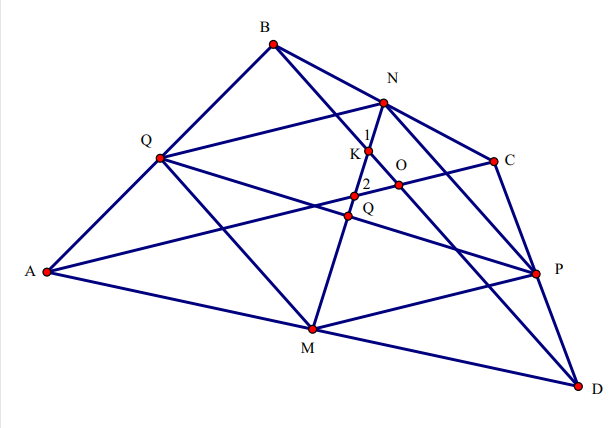
Gọi Q, P lần lượt là trung điểm của AB, CD tương ứng

Khi đó ta có:

QN // MP; NP // QM => Tứ giác QNPM là hình bình hành.

Vì MN tạo với AC và BD hai góc bằng nhau nên suy ra MN cũng tạo với QN và QM hai góc bằng nhau

Tức là: \(\widehat {QNM} = \widehat {QMN}\)

Suy ra tam giác QMN cân tại Q

Suy ra QN = QM

Ta có QN = \(\frac{1}{2}\)AC và QM = \(\frac{1}{2}\)BD (đường trung bình của tam giác)

Mà QN = QM (chứng minh trên)

Suy ra AC = BD

Vậy tứ giác trên có hai đường tréo bằng nhau.

Bài 2. Hình thang

A. Lý thuyết

1. Định nghĩa: Tứ giác ABCD là hình thang \( \Leftrightarrow \left[ \begin{array}{l}AB//CD\\BC//AD\end{array} \right.\)

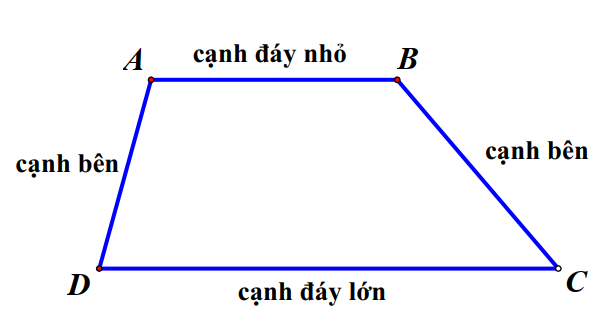
2. Tính chất:

Nếu một hình thang có hai cạnh bên song song thì nó là hình chữ nhật.

Nếu một hình thang có hai bạnh đáy bằng nhau thì nó là hình bình hành.

3. Hình thang vuông:

Hình thang vuông là hình thang có hai góc vuông.

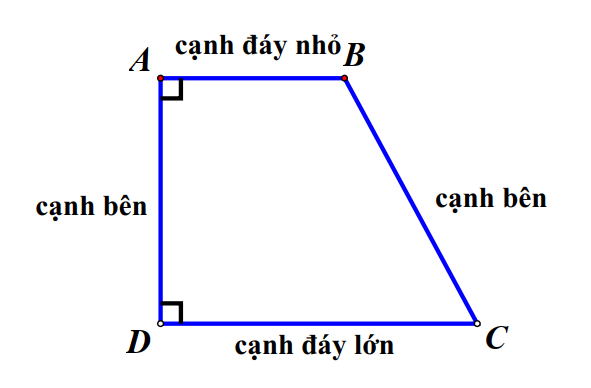
B. Luyện kĩ năng giải bài tập

Bài 7. Cho tứ giác ABCD có AC = DC, đường chéo AC là phân giác góc \(\widehat A\). Chứng minh rằng ABCD là hình thang.

Bài giải:

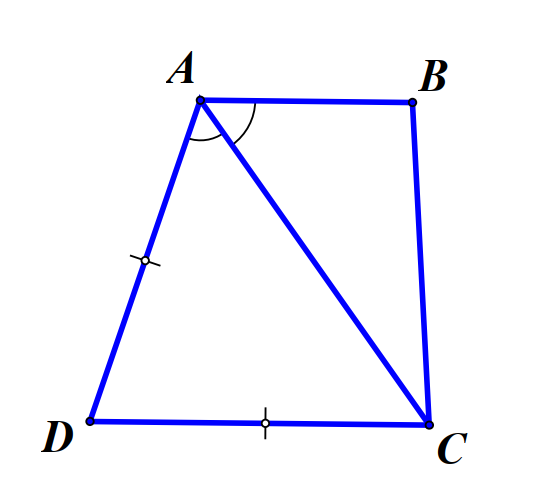
Ta có AD = DC nên tam giác ADC cân tại D.

Suy ra \(\widehat {DCA} = \widehat {DAC} = \widehat {BAC}\)

Suy ra AB // CD (hai góc so le trong bằng nhau)

Vậy ABCD là hình thang.

Bài 8. Cho hình thang ABCD, đáy AB = 40cm, CD = 50cm, AD = 30cm. Chứng minh rằng ABCD là hình thang vuông.

Bài giải:

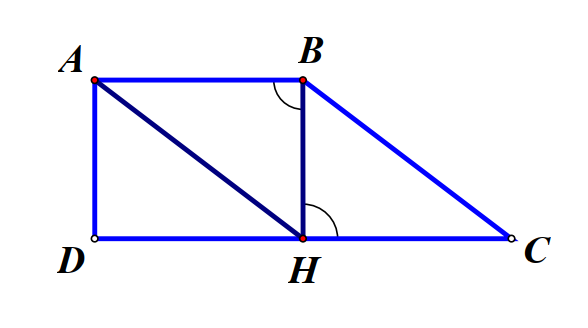
Gọi H là trung điểm của CD. Ta có DH = CH = 40cm

Xét hai tam giác ABH và CHB có:

AB = CH = 40cm, \(\widehat {ABH} = \widehat {CHB}\) (so le trong), BH = HB

Suy ra AH = CB = 50cm.

Tam giác ADH có: \(A{D^2} + D{H^2} = {40^2} + {30^2} = {50^2} = A{H^2}\)

Suy ra tam giác ADH vuông tại D. Vậy hình thang ABCD là hình thang vuông.

Bài 9. Cho hình thanh ABCD (AD//BC; AD > BC) có đường chéo AC và BD vuông góc với nhau tại I. Trên đáy AD lấy M sao cho AM bằng độ dài đường trung bình của hình thang

Chứng minh: tam giác ACM cân tại M

Bài giải: