Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập vận dụng cao vectơ, tích vô hướng của hai vectơ và ứng dụng, tài liệu bao gồm 170 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

Vận dụng cao vecto – tích vô hướng

Vấn đề 1. Biểu diễn véc tơ

Vấn đề 2. Ba điểm thẳng hàng

Vấn đề 3. Quỹ tích

Vấn đề 4. Tỉ lệ

Vấn đề 5. Min,max

Vấn đề 6 tích vô hướng

Bài tập vận dụng cao vectơ, tích vô hướng của hai vectơ và ứng dụng

Vấn đề 1. Biểu diễn véc tơ

Câu 1: Cho tam giác ABC biết \(AB = 3,BC = 4,AC = 6,I\) là tâm đường tròn nội tiếp tam giác ABC Gọi x, y, z là các số thực dương thỏa mãn \(x \cdot \overrightarrow {IA}  + y \cdot \overrightarrow {IB}  + z \cdot \overrightarrow {IC}  = \vec 0\). Tính \(P = \frac{x}{y} + \frac{y}{z} + \frac{z}{x}\)

A. \(P = \frac{3}{4}\).

B. \(P = \frac{{41}}{{12}}\).

C. \(P = \frac{{23}}{{12}}\).

D. \(P = \frac{2}{3}\).

Câu 2: Cho hình bình hành ABCD. Gọi I là trung điểm của D, G là trọng tâm tam giác BCI. Đặt \(\vec a = \overrightarrow {AB} ,\vec b = \overrightarrow {AD} \). Hãy tìm đẳng thức đúng trong các đẳng thức sau?

A. \(\overrightarrow {AG}  = \frac{5}{6}\vec a + \frac{2}{3}\vec b\).

B. \(\overrightarrow {AG}  = \frac{5}{6}\vec a + \vec b\).

C. \(\overrightarrow {AG}  = \vec a + \frac{5}{6}\vec b\).

Câu 3: Cho tam giác ABC với các cạnh \(AB = c,BC = a,CA = b\). Gọi I là tâm đường tròn nội tiếp tam giác ABC. Đẳng thức nào sau đây đúng.

A. \(a\overrightarrow {IA}  + b\overrightarrow {IB}  + c\overrightarrow {IC}  = \vec 0\)

B. \(b\overrightarrow {IA}  + c\overrightarrow {IB}  + a\overrightarrow {IC}  = \vec 0\)

C. \(c\overrightarrow {IA}  + b\overrightarrow {IB}  + a\overrightarrow {IC}  = \vec 0\)

D. \(c\overrightarrow {IA}  + a\overrightarrow {IB}  + b\overrightarrow {IC}  = \vec 0\)

Câu 4: Cho hình thang cân ABCD có CD là đáy lớn, $\widehat{ADC}={30}^{°}$. Biết \({\rm{DA}} = {\rm{a}},{\rm{DC}} = {\rm{b}}\), hãy biểu diễn \(\overrightarrow {DB} \) theo hai vecto \(\overrightarrow {DA} \) và \(\overrightarrow {DC} \).

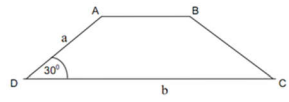
A. \(\overrightarrow {DB}  = \overrightarrow {DA}  + \overrightarrow {DC} \)

B. \(\overrightarrow {DB}  = \overrightarrow {DA}  + \frac{{b - a\sqrt 3 }}{b}\overrightarrow {DC} \).

C. \(\overrightarrow {DB}  = \overrightarrow {DA}  + \frac{{b - a}}{b}\overrightarrow {DC} \).

D. \(\overrightarrow {DB}  = b\overrightarrow {DA}  + a\overrightarrow {DC} \).

Câu 5: Cho hình bình hành ABCD, M là điểm thỏa mãn \(5\overrightarrow {AM}  + 2\overrightarrow {CA}  = \vec 0\). Trên các cạnh AB,BC lần lượt lấy các điểm P, Q sao cho \(MP//BC,MQ//AB\). Gọi N là giao điểm của AQ và CP. Giá trị của tổng \(\frac{{AN}}{{AQ}} + \frac{{CN}}{{CP}}\) bằng:

A. \(\frac{{21}}{{19}}\)

B. \(\frac{{24}}{{19}}\)

C. \(\frac{{23}}{{19}}\)

D. \(\frac{{25}}{{19}}\)

Câu 6: Cho tứ giác ABCD, M là điểm tùy ý. K là điểm cố định thỏa mãn đẳng thức \(\overrightarrow {{\rm{MA}}}  + \overrightarrow {{\rm{MB}}}  + \overrightarrow {{\rm{MC}}}  + 3\overrightarrow {{\rm{MD}}}  = x\overrightarrow {{\rm{MK}}} \). Tìm x :

A. 2 .

B. 6 .

C. 5 .

D. 4 .

Câu 7: Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm N sao cho \(AM = 3MC,NC = 2NB\). Gọi O là giao điểm của AN và BM. Tính diện tích tam giác ABC biết diện tích tam giác OBN bằng 1 .

A. 24 .

B. 20 .

C. 30 .

D. 45

Câu 8: Cho tam giác ABC, gọi I là điểm trên BC kéo dài sao cho \(IB = 3IC\). Gọi J, K lần lượt là những điểm trên cạnh AC, AB sao cho \(JA = 2JC;KB = 3KA\). Khi đó \(\overrightarrow {BC}  = m \cdot \overrightarrow {AI}  + n \cdot \overrightarrow {JK} \). Tính tổng P=m + n ?

A. \(P = 34\).

B. \(P =  - 34\).

C. \(P =  - 14\).

D. \(P = 14\).

Câu 9: Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho \(\overrightarrow {AM}  = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {DN}  = \frac{1}{2}\overrightarrow {DC} \). Gọi I và J là các điểm thỏa mãn \(\overrightarrow {BI}  = m\overrightarrow {BC} ,\overrightarrow {AJ}  = n\overrightarrow {AI} .\)

Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu?

A. \(\frac{1}{3}\)

B. 3

C. \(\frac{2}{3}\)

D. 1

Câu 10: Cho tam giác ABC, trên cạnh AB lấy điểm M, trên cạnh BC lấy N sao cho \({\rm{AM}} = 3{\rm{MB}}\), \({\rm{NC}} = 2{\rm{BN}}\). Gọi I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam giác ICN bằng 2 .

A. \(\frac{3}{2}\)

B. \(\frac{{33}}{2}\)

C. 11

D. \(\frac{9}{{11}}\)

Câu 11: Cho  có trọng tâm G và hai điểm M,N thỏa mãn: \(3\overrightarrow {MA}  - 2\overrightarrow {CM}  = \vec 0,\overrightarrow {NA}  - 2\overrightarrow {NB}  = \vec 0\). Chọn mệnh đề đúng.

A. \(\overrightarrow {NG}  = 4\overrightarrow {GM} \).

B. \(\overrightarrow {NG}  = 5\overrightarrow {GM} \).

C. \(\overrightarrow {NG}  = 6\overrightarrow {GM} \).

D. \(\overrightarrow {NG}  = 7\overrightarrow {GM} \).

Câu 12: (Đẳng thức vec tơ) Cho tam giác ABC. Gọi \({{\rm{A}}^\prime },{{\rm{B}}^\prime },{{\rm{C}}^\prime }\) là các điểm xác định bởi \(2018\overrightarrow {{A^\prime }B}  + 2019\overrightarrow {{A^\prime }C}  = \vec 0,2018\overrightarrow {{B^\prime }C}  + 2019\overrightarrow {{B^\prime }A}  = \vec 0,2018\overrightarrow {{C^\prime }A}  + 2019\overrightarrow {{C^\prime }B}  = \vec 0\). Khi đó, mệnh đề nào sau đây đúng?

A.  và  có cùng trọng tâm.

B. .

C. .

D.  và  có cùng trực tâm.

Câu 13: ( tính độ dài vec tơ) Cho tam giác đều ABC cạnh a. Gọi điểm M là trung điểm BC. Tính độ dài của vec to \(\frac{1}{2}\overrightarrow {AB}  + 2\overrightarrow {AC} \)

A. \(\frac{{a\sqrt {21} }}{3}\).

B. \(\frac{{a\sqrt {21} }}{2}\).

C. \(\frac{{a\sqrt {21} }}{4}\).

D. \(\frac{{a\sqrt {21} }}{7}\).

Câu 14: Cho  có M là trung điểm của BC,H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm x để \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = x\overrightarrow {HO} \).

A. \(x = 2\).

B. \(x =  - 2\).

C. \(x = 1\).

D. \(x = 3\).

Câu 15: Cho tam giác ABC có đường trung tuyến CM vuông góc với phân giác trong AL. Giả sử ngoài ra còn có \(CM = kAL\). Biết \(\cos A = \frac{{a + b{k^2}}}{{c + d{k^2}}}\). Tính \(a + b + c + d\)

A. 18 .

B. 5 .

C. 26 .

D. 17 .

Câu 16: Cho tam giác ABC. Gọi M, N, P là các điểm lần lượt thỏa mãn \(\overrightarrow {MA}  + 3\overrightarrow {MB}  = \vec 0,\overrightarrow {AN}  = \frac{1}{3}\overrightarrow {AC} \), \(2\overrightarrow {PB}  + 3\overrightarrow {PC}  = \vec 0\) Gọi K là giao điểm của AP và M N. Trong các mệnh đề sau, mệnh đề nào đúng?

\[{\rm{\;A}}{\rm{.\;}}4\overrightarrow {KA}  + 5\overrightarrow {KP}  = \vec 0{\rm{.\;}}\]

B. \(3\overrightarrow {KA}  + 2\overrightarrow {KP}  = \vec 0\)

C.\(\begin{array}{*{20}{l}}{{\rm{ }}\overrightarrow {KA}  + \overrightarrow {KP}  = \vec 0}&{\rm{ }}\end{array}\)

D. \(\overrightarrow {KA}  = \overrightarrow {KP} {\rm{.}}\)

Câu 17: Cho hình thang \({\mathop{\rm ABCD}\nolimits} (AB//CD)\) có hai đường chéo vuông góc với nhau. Biết \(AB + CD = 20\;{\rm{cm}}\). Tìm \(|\overrightarrow {AC}  + \overrightarrow {BD} |\).

A. \(40\;{\rm{cm}}\).

B. \(20\;{\rm{cm}}\).

C. \(30\;{\rm{cm}}\).

D. \(10\;{\rm{cm}}\).

Câu 18: Cho tam giác ABC có \(AB = 3;AC = 4\). Gọi AD là đường phân giác trong của góc A.Biết \(\overrightarrow {AD}  = m\overrightarrow {AB}  + n\overrightarrow {AC} \). Khi đó tổng m + n có giá trị là:

A. 1

B. \( - 1\)

C. \(\frac{1}{7}\)

D. \( - \frac{1}{7}\)

Câu 19: Cho tam giác ABC bất kỳ, gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA. \({H^\prime }{H^\prime }\) lần lượt là trực tâm các tam giác ABC, MNP. Khẳng định nào đúng trong các khẳng định sau?

A. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 3\overrightarrow {H{H^\prime }} \).

B. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 2\overrightarrow {H{H^\prime }} \).

C. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = \vec 0\).

D. \(\overrightarrow {HM}  + \overrightarrow {HN}  + \overrightarrow {HP}  = 3\overrightarrow {H{H^\prime }} \).

Câu 20: Cho tam giác đều ABC tâm O. M là một điểm bất kì bên trong tam giác. Gọi D,E,F lần lượt là hình chiếu của M lên BC, CA, AB . Với giá trị nào của k ta có hệ thức:

$\(\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF}  = k\overrightarrow {MO} \)$

A. \(k = \frac{1}{2}\).

B. \(k = 1\).

C. \(k = \frac{3}{2}\).

D. \(k = 2\)

Câu 21: Một giá đỡ hình tam được gắn vào tường (như hình vẽ). Tam giác ABC vuông cân tại B. Người ta treo vào điểm A một vật nặng 10N. Tính độ lớn của các lực tác động vào tường tại B và C ? (Bỏ qua khối lượng của giá đỡ)

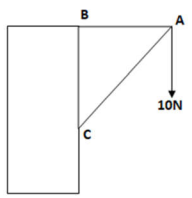
A. \({F_B} = 10\sqrt 2 N,{F_C} = 10N\)

B. \({F_B} = 10N,{F_C} = 10\sqrt 2 \)

C. \({F_B} = {F_C} = 10\;{\rm{N}}\)

D. \({F_B} = 10N,{F_C} =  - 10\sqrt 2 \)

Câu 22: Cho ba điểm A,B,C thuộc đường tròn tâm O, thỏa mãn \(\overrightarrow {OA}  + \overrightarrow {OC}  + \overrightarrow {OB}  = \vec 0\). Tính góc \(\widehat {AOB}\) ?

A. $\widehat{AOB}={120}^{°}$.

B. $\widehat{AOB}={90}^{°}$.

C. $\widehat{AOB}={150}^{°}$.

D. $\widehat{AOB}={30}^{°}$.

Câu 23: Cho tam giác AC$. Điểm M trên cạnh BC thỏa mãn \(\overrightarrow {AM}  = \frac{1}{3} \cdot \overrightarrow {AB}  + \frac{2}{3} \cdot \overrightarrow {AC} \), khẳng định nào sau đây là khẳng định đúng?

A. \(\overrightarrow {MB}  = 2\overrightarrow {MC} \).

B. \(MB = 2MC\).

C. \(MC = 2MB\).

D. \(\overrightarrow {MC}  =  - 3\overrightarrow {MB} \).

Câu 24. Cho tam giác đều ABC nội tiếp đường tròn tâm O, M là một điểm tùy ý nằm bên trong tam giác đã cho; gọi \(A',B',C'\) theo thứ tự là hình chiếu vuông góc của M lên các cạnh B  ; CA và AB. Khi đó ta có đẳng thức vectơ \[k\left( {\overrightarrow {MA'}  + \overline {MB'}  + \overrightarrow {MC'} } \right) = l\overline {MO} ,k.l \ne 0,\frac{k}{l}\] là phân số tối giản. Tính \(2{k^2} - {l^2}\).

A. \(2{k^2} - {l^2} = 1\).

B. \(2{k^2} - {l^2} =  - 1\).

C. \(2{k^2} - {l^2} = 14\).

D. \(2{k^2} - {l^2} =  - 5\).

Câu 25: Cho hình vuông ABCD, E,F thõa mãn \(\overrightarrow {BE}  = \frac{1}{3}\overrightarrow {BC} ;\overrightarrow {CF}  =  - \frac{1}{2}\overrightarrow {CD} ;AE \cap BF = I\) Ta có \(\overrightarrow {AI}  = k\overrightarrow {AB}  + l\overrightarrow {AD} \). Khi đó tỉ số k,l thõa mãn cặp nào sau:

A. \(k = \frac{3}{5};l = \frac{2}{5}\)

B. \(k = \frac{6}{5};l = \frac{2}{5}\)

C. \(k = \frac{5}{6};l = \frac{3}{6}\)

D. \(k =  - \frac{6}{5};l = \frac{1}{3}\)

Câu 26: Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm \[\] sao cho: \(AM = 3MC,NC = 2NB\), gọi O là giao điểm của AN và BM. Tính diện tích  biết diện tích  bằng 1 .

A. 10 .

B. 20 .

C. 25 .

D. 30 .

Câu 27: Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng định đúng?

A. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 4\overrightarrow {HO} \).

B. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 2\overrightarrow {HO} \).

C. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = \frac{2}{3}\overrightarrow {HO} \)

D. \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = 3\overrightarrow {HO} \).