Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Phương pháp tọa độ trong không gian mức độ nhận biết Toán học 12 chọn lọc, có đáp án. Tài liệu có 40 trang gồm 60 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán học 12. Hi vọng với bộ câu hỏi trắc nghiệm Phương pháp tọa độ trong không gian mức độ nhận biết có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán học 12.
Trắc nghiệm Hệ tọa độ trong không gian có đáp án – Toán 12
Câu 1: Trong không gian Oxyz , cho vectơ a→ = (2; 1; -2) . Tìm tọa độ của các vectơ b→ cùng phương với vectơ a→ và có độ dài bằng 6.
Ta có:
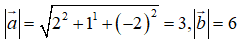
Mặt khác hai vectơ này cùng phương nên ta có:
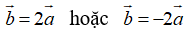
Từ đó ta suy ra
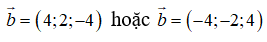
Vậy đáp án cần tìm là C.
Lưu ý. Đáp án D là sai, do sai lầm trong tính độ dài của vectơ a→ :
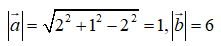
Mà hai vectơ này cùng phương nên ta có:
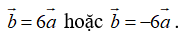
Câu 2: Trong không gian Oxyz, cho hai vectơ
Với những giá trị nào của m thì sin(a→, b→) đạt giá trị lớn nhất
A. m=1 C. m=-8
B. m=1 hoặc m=-8 D. Không tồn tại m thỏa mãn.
Với mọi cặp vectơ
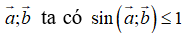
Dấu bằng xảy ra khi và chỉ khi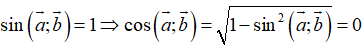 
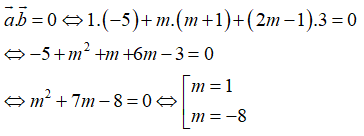
hay hai vectơ này vuông góc. Điều đó tương đương với điều kiện :
Chọn B.
Nếu chúng ta suy nghĩ sai là: ‘‘ sin(a→, b→) đạt giá trị lớn nhất khi và chỉ khi góc giữa hai vectơ đó lớn nhất ’’ thì khi đó góc giữa hai vectơ bằng 180o , do đó tồn tại số k âm sao cho :
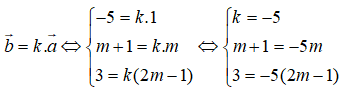
Hệ này vô nghiệm và dẫn đến ta chọn đáp án là D.
Câu 3: Trong không gian Oxyz , gọi φ là góc tạo bởi hai vectơ a→ = (4; 3; 1); b→ = (-1; 2; 3). Trong các khẳng định sau, khẳng định nào đúng?
Ta có
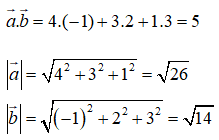
Suy ra
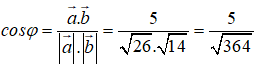
Vậy đáp án đúng là A.
Lưu ý. Đáp án B sai do tính nhầm
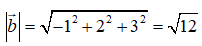
Đáp án C sai do tính nhầm
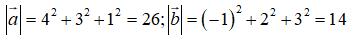
Đáp án D sai do tính nhầm
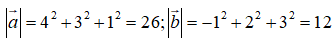
Câu 4: Trong không gian Oxyz , cho hình bình hành ABDC với A(0;0;0), B(1;-2;3), D(3;1;-4). Tọa độ của điểm C là:
A. (4;-1;-1) B. (2;3;-7) C. (3/2; 1/2; -2) D. (-2;-3;7)
Vì ABDC là hình bình hành nên ta có:
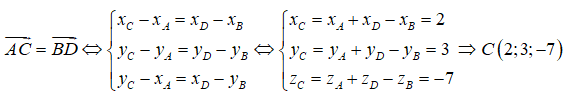
Vậy đáp án đúng là B.
Lưu ý. Đáp án A sai do nhầm giải thiết ABCD là hình bình hành.
Đáp án C xuất phát từ việc vận dụng sai quy tắc hình bình hành
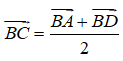
Đáp án D xuất phát từ sai lầm cho rằng: AC→ = DB
Câu 5: Trong không gian Oxyz , cho hình hộp ABCD.A'B'C'D' có A(1;0;0), B(1;2;0), D(2;-1;0), A’(5;2;2). Tọa độ điểm C’ là:
A. (3;1;0) B. (8;3;2) C. (2;1;0) D. (6;3;2)
Vì ACC’A’, ABCD là những hình bình hành nên áp dụng quy tắc hình bình hành ta có:
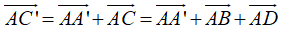
Từ đó suy ra:
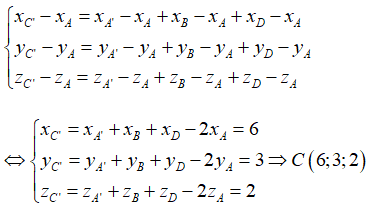
Vậy đáp án đúng là D.
Lưu ý. Đáp án A sai do cho rằng tọa độ của C’ là tổng tọa độ của hai điểm B và D.
Đáp án B sai do cho rằng tọa độ của C’ là tổng tọa độ của ba điểm B, D và A’
Đáp án C xuất phát từ sai lầm rằng
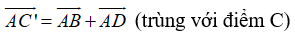
Câu 6: Cho hai vectơ a→, b→ thay đổi nhưng luôn thỏa mãn:
Giá trị nhỏ nhất của
A. 11 B. -1 C. 1 D. 0
Áp dụng bất đẳng thức vectơ
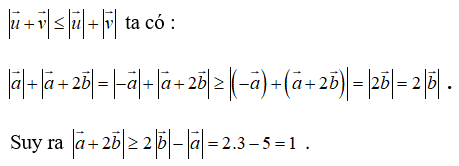
Dấu bằng xảy ra khi 2 vectơ
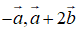
cùng hướng. Vậy độ dài của vectơ |a→ - 2b→| ≥ 0 nhỏ nhất bằng 1.
Suy ra đáp án đúng là C.
Lưu ý. Đáp án A là giá trị lớn nhất của
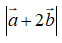
Đáp án B xuất phát từ bất đẳng thức
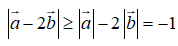
tuy nhiên đáp án B sai do độ dài của một vectơ không âm
Đáp án D xuất phát từ nhận xét
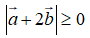
tuy nhiên trong trường hợp này dấu bằng không xảy ra
Câu 7: Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x2 + y2 + z2 - 2x - 2y - 4z + 5 = 0
Trong các khẳng định sau, khẳng định nào sai?
A. Mặt cầu (S) có tâm I(1;1;2) và đường kính có độ dài bằng 2.
B. Phương trình chính tắc của mặt cầu (S) là: (x - 1)2 + (y - 1)2 + (z - 2)2 = 1
C. Diện tích của mặt cầu (S) là π
D. Thể tích của khối cầu (S) là 4π/3
Ta viết lại phương trình của (S) dưới dạng chính tắc như sau:
x2 + y2 + z2 - 2x - 2y - 4z + 5 = 0
<=> (x2 - 2x + 1) +(y2 - 2y + 1) + (z2 - 4z + 4) = 1 + 1 + 4 - 5
<=> (x - 1)2 + (y - 1)2 + (z - 2)2 = 1
Vậy khẳng định B đúng.
Mặt cầu (S) có tâm I(1;1;2) và có bán kính R=1, do đó đường kính của (S) là 2R=2.
Vậy khẳng định A đúng.
Thể tích của khối cầu (S) là
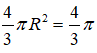
Vậy khẳng định D đúng
Khẳng định C là sai do nhầm giữa công thức diện tích của mặt cầu với diện tích của đường tròn. Diện tích mặt cầu (S) là: 4πR2 = 4π
Câu 8: Trong không gian Oxyz, cho tứ diện đều ABCD có A(0;1;2). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD). Cho H(4;-3;-2). Tọa độ tâm I và bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD là:
A. I(2; -1; 0); R = 2√3 C. I(3; -2; -1); R = 3√3
B. I(4; -3; -2); R = 4√3 D. I(3; -2; -1); R = 9
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
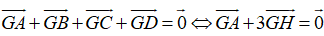
Từ đó ta có:
Vậy đáp án C đúng
Lưu ý. Đáp án A sai do nhận định I là trung điểm của AH
Đáp án B sai do cho rằng I trùng H
Đáp án D sai do tính toán nhầm bán kính R
Câu 9: Trong không gian Oxyz, cho hai vectơ u→ = (x; y; z), v→ = (x'; y'; z') . Khẳng định nào dưới đây sai?
Câu 10: Trong không gian Oxyz, cho hai vectơ u→ = (x; y; z), v→ = (x'; y'; z') khác 0→ . Khẳng định nào dưới đây sai?
Câu 11: Trong không gian Oxyz, trong các khẳng định dưới đây, khẳng định nào đúng với mọi u→, v→ ?
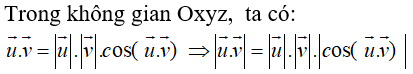
Câu 12: Trong không gian Oxyz, cho hai vectơ a→ = (x1; y1; z1), b→ = (x2; y2; z2) thay đổi. Trong các khẳng định dưới đây, khẳng định nào đúng?
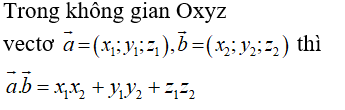
Câu 13: Trong không gian Oxyz, cho ba vectơ
Trong các khẳng định sau, khẳng định nào đúng?
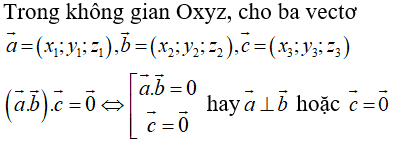
Câu 14: Trong không gian Oxyz, cho ba vectơ
Trong các khẳng định sau, khẳng định nào đúng?
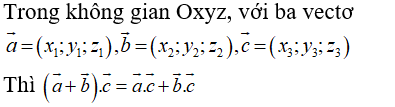
Câu 15: Trong không gian Oxyz, cho ba vectơ
Câu 16: Trong không gian Oxyz, cho ba vectơ
Trong các khẳng định sau, khẳng định nào đúng?
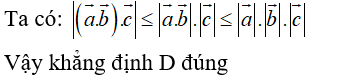
Câu 17: Trong không gian Oxyz, cho hai vectơ a→ = (x1, y1, z1), 2→ = (x2, y2, z2) thay đổi. Trong các khẳng định dưới đây, khẳng định nào đúng?
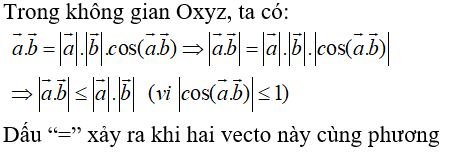
Câu 18: Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A(xA; yA, zA), B(xB; yB, zB), CA(xC; yC, zC) . Gọi M là trung điểm của BC, G là trọng tâm tam giác ABC. Khẳng định nào sau đây là sai?
Câu 19: Trong không gian Oxyz, cho hai điểm A, B có tọa độ các điểm A(xA; yA, zA), B(xB; yB, zB). Tọa độ trung điểm M của đoạn thẳng AB là:
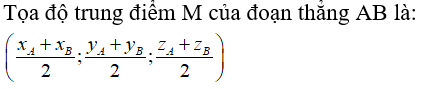
Câu 20: Trong không gian Oxyz, cho tam giác ABC có A(1;2;0), B(-4;5;3), C(3;-10;-6). Tọa độ trọng tâm G của tam giác ABC là:
A. (0;-1;-1) B. (0;-3;-3) C.(0;-2;-2) D. Đáp án khác
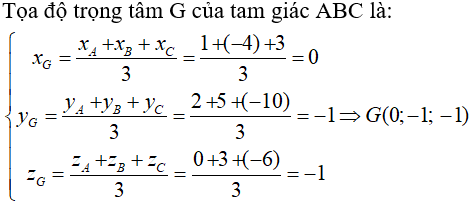
Câu 21: Trong không gian Oxyz, cho tam giác ABC có A(2;3;-1), B(1;3;2), G(2;-3;-1) là trọng tâm của tam giác ABC. Tọa độ của điểm C là:
A. (3;-15;-4) B. (-1;-9;-2) C. (-3;15;4) D. (1;9;2)
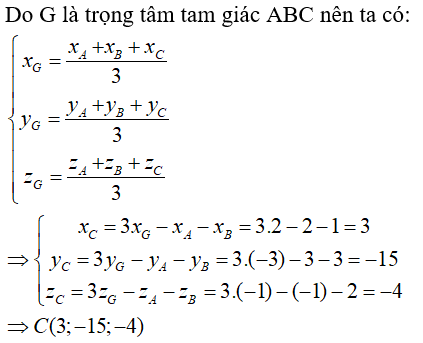
Câu 22: Trong không gian Oxyz, cho ba vectơ
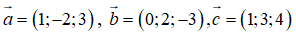
Tọa độ của vectơ
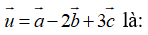
A. (4;3;9) B. (4;3;21) C. (2;-1;10) D. (4;-1;10)
Câu 23: Trong không gian Oxyz, cho hai điểm A(1;3;-1), B(5;4;-4). Khoảng cách giữa hai điểm A và B là:
A. (4; 1; -3) B. √26 C. 2√2 D. √66
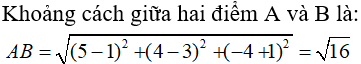
Câu 24: Cho hai vectơ a→, b→ tạo với nhau một góc 120o. Biết độ dài của hai vectơ đó lần lượt là 4 và 3. Độ dài của vectơ tổng a→ + b→ là:
A. 7 B. 1 C. √13 D. √37
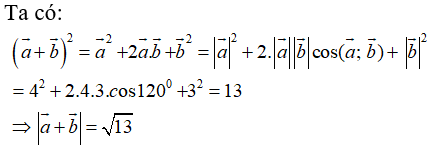
Câu 25: Cho hai vectơ a→, b→ tạo với nhau một góc 60o . Biết độ dài của hai vectơ đó lần lượt là 5 và 10. Độ dài của vectơ hiệu a→ - b→ là:
A. 15 B. 5 C. 75 D. √75
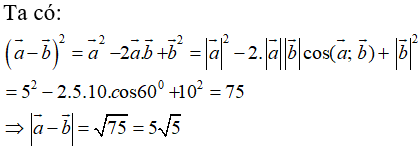
Câu 26: Trong không gian Oxyz, cho hai điểm A(2;2;2), B(-4;-4;-4). Điểm nào dưới đây nằm trên đường thẳng AB?
A. M1(-1; 1; -1) B. M2(1; -1; -1) C. M3(-1; -1; 1) D. M4(-1; -1; -1)
Ba điểm A, B, M thẳng hàng khi và chỉ khi hai vecto AB→; AM→ cùng phương
Ta có: 
Do đó, ba điểm A, B, M4 thẳng hàng hay điểm M4 nằm trên đường thẳng AB.
Câu 27: Trong không gian Oxyz, cho hai điểm A(1;2;-3), B(3;6;-9). Điểm nào dưới đây không nằm trên đường thẳng AB?
A. M1(2; 4; -6) B. M2(-1; -2; 3) C. M3(0; 0; 1) D. M4(5; 10; -15)
Để ba điểm A, B, M không thẳng hàng khi và chỉ khi hai vecto AB→; AM→ không cùng phương
Ta có: 
Do đó,hai vecto này không cùng phương
Suy ra ba điểm A, B, M3 không thẳng hàng hay điểm M3 không nằm trên đường thẳng AB.
Câu 28: Trong không gian Oxyz, cho ba điểm A(2;1;-3), B(4;2;-6), C(10;5;-15). Khẳng định nào sau đây là đúng?
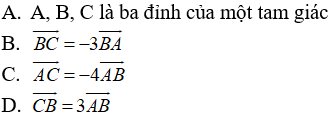
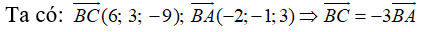
Câu 29: Trong không gian Oxyz, cho hai vectơ a→ = (1; -2; -3), b→ = (m; 2m - 1; 1) . Với những giá trị nào của m thì hai vectơ a→ và b→ vuông góc?
A. m = -1/3 B. m = -1/2 C. m = 1 D. m = 0
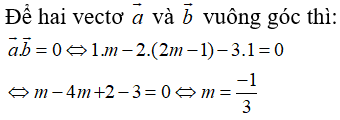
Câu 30: Trong không gian Oxyz, cho hai vectơ a→ = (1; m; 2m - 1), b→ = (m + 1; m2 + 1; 4m - 2) . Với những giá trị nào của m thì cos(a→, b→) đạt giá trị lớn nhất?
A. m = 1/2 C. m = 1
B. m = 1 hoặc m = 1/2 D. Không tồn tại m thỏa mãn
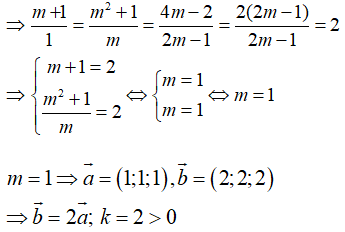
Câu 31: Trong không gian Oxyz, cho hai vectơ a→ = (1; -2; 2), b→ = (-2; m - 3; m) . Với những giá trị nào của m thì hai vectơ a→ và b→ có độ dài bằng nhau?
A. m = 1 hoặc m = 2 C. m = 2
B. m = 1 D. Không có m
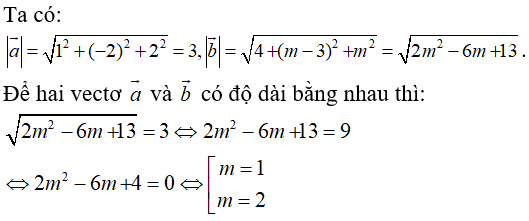
Câu 32: Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:
A. A(1; 0; 0), B(0; 2; 0), C(0; 0; 3) C. A(-3; 0; 0), B(0; -6; 0), C(0; 0; -9)
B. A(3; 0; 0), B(0; 6; 0), C(0; 0; 9) D. A(6; 0; 0), B(0; 3; 0), C(0; 0; 9)
Do A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz nên A(a; 0; 0); B(0; b; 0) và C(0; 0; c).
Mà điểm G(1;2;3) là trọng tâm của tam giác ABC nên:
Câu 33: Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?
A. A(1; 2; 3), B(5; -4; -1), C(3; -1; 1) C. A(1; 2; 3), B(5; -4; -1), C(9; -10; -5)
B. A(1; 2; 3), B(5; -4; -1), C(6; -2; 2) D. A(1; 2; 3), B(5; -4; -1), C(-3; 8; 7)
Để ba điểm A, B,C lập thành ba đỉnh của 1 tam giác khi và chỉ khi ba điểm A, B,C không thẳng hàng hay hai vecto AB→; AC→ không cùng phương
Xét phương án B ta có:
AB→ = (4; -6; -4); AC→ = (5; -4; -1)
Suy ra hai vecto này không cùng phương hay 3 điểm A, B, C không thằng hàng.
Câu 34: Cho hai vectơ a→, b→ thay đổi nhưng luôn thỏa mãn
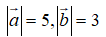
Giá trị nhỏ nhất của: 
A. 11 B. -1 C. 1 D. √61
Sử dụng bất đẳng thức vectơ:
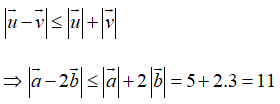
Dấu bằng xảy ra khi và chỉ khi hai vectơ này ngược hướng. Suy ra đáp án A.
Hai đáp án B và C xuất phát từ sai lầm
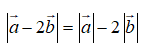
Đáp án D xuất phát từ sai lầm
Câu 35: Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện x2 + y2 + z2 = 4, m2 + n2 + p2 = 9. Vectơ AB→ có độ dài nhỏ nhất là:
A. 5 B. 1 C. 13 D. Không tồn tại
Từ giả thiết suy ra
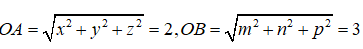
Do đó AB ≥ |OA - OB| = 1. Dấu bằng xảy ra khi O nằm ngoài đoạn AB. Suy ra đáp án đúng là B.
Hai đáp án A, D sai do nhầm OA = x2 + y2 + z2 = 4; OB = m2 + n2 + p2 = 9
Đáp án C sai do nhầm với câu hỏi vectơ AB→ có độ dài lớn nhất
Câu 36: Trong không gian Oxyz, cho hình bình hành ABCD với A(0;1;-2), B(3;-2;1), D(1;4;2). Tọa độ của điểm C là:
A. (4;1;5) B. (4;3;1) C. (4;2;3) D. (4;1;1)
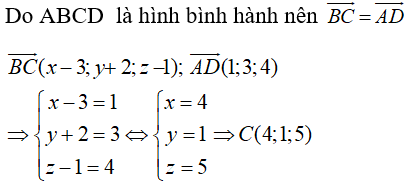
Câu 37: Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D' có A(0;0;0), B(1;2;0), D(2;-1;0), A’(5;2;3). Tọa độ của điểm C’ là:
A. (3;1;0) B. (8;3;3) C. (-8;-3;-3) D. (-2;-1;-3)
Sử dụng quy tắc hình hộp trong không gian:
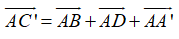
Ta có:
Câu 38: Trong không gian Oxyz, cho vectơ a→ = (1; -2; 3) . Tìm tọa độ của vectơ b→ biết rằng vectơ b→ ngược hướng với vectơ a→ và |b→| = 2|a→|
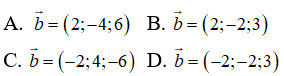
Vì vectơ b→ ngược hướng với vectơ a→ và |b→| = 2|a→| nên:
b→ = -2a→ = (-2; 4; -6)
Câu 39: Trong không gian Oxyz, cho vectơ a→ = (-1; -2; 3) . Tìm tọa độ của vectơ b→ = (2; y; z) biết rằng vectơ b→ cùng phương với vectơ a→
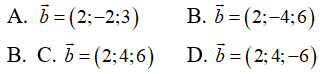
Vectơ b→ cùng phương với vectơ a→ khi và chỉ khi tồn tại một số thực k thỏa mãn:
Câu 40: Trong không gian Oxyz, cho vectơ a→ = (m; m + 3; 3 - 2m). Với giá trị nào của m thì vectơ a→ có độ dài nhỏ nhất
A. m = 1/2 B. m = 0 C. m = 1 D. m = -3
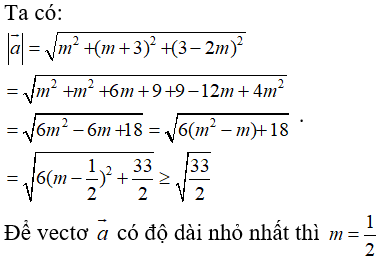
Câu 41: Trong không gian Oxyz, cho hai vectơ u→ = (3; 4; 0), v→ = (2; -1; 2) . Tích vô hướng của hai vectơ u→ và v→ là:
A. 15 B. 2 C. 3 D. 0
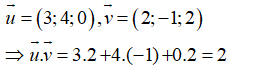
Câu 42: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(x - 1)2 + (y + 2)2 + (z + 3)2 = 25
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -3); R = 25 C. I(-1; 2; 3); R = 25
B. I(-1; 2; 3); R = 5 D. I(1; -2; -3); R = 5
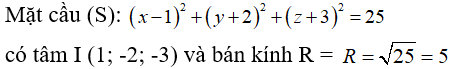
Câu 43: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
x2 + y2 + z2 - 2x + 4y + 4z + 5 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -2); R = 2 C. I(-1; 2; 2); R = 2
B. I(1; -2; -2); R = 4 D. I(-2; 4; 4); R = 4
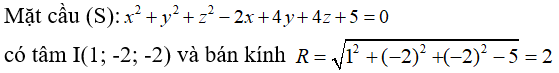
Câu 44: Phương trình nào dưới đây là phương trình của một mặt cầu?
A. x2 + y2 + z2 - 2x + 4y - 8z - 25 = 0
B. x2 + y2 + z2 - 2x - 4y - 6z + 15 = 0
C. 3x2 + 3y2 + 3z2 - 6x - 7y - 8z + 1 = 0
D. (x - 1)2 + (y + 2)2 + (z + 3)2 + 10 = 0
Sử dụng phương trình x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 là phương trình của một mặt cầu khi và chỉ khi a2 + b2 + c2 - d > 0
+ Phương án A và B không thỏa mãn điều kiện a2 + b2 + c2 - d > 0
+ Phương án C: 3x2 + 3y2 + 3z2 - 6x - 7y - 8z + 1 = 0
Nên đây có là phương trình mặt cầu.
+ Phương án D: (x - 1)2 + (y - 2)2 + (z - 3)2 + 10 = 0
⇔ (x - 1)2 + (y - 2)2 + (z - 3)2 = -10 nên không là phương trình mặt cầu.
Câu 45: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
3x2 + 3y2 + 3z2 + 6x - 8y + 15z - 3 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
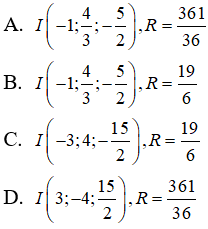
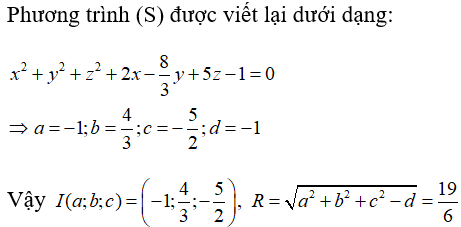
Câu 46: Trong không gian Oxyz, cho mặt cầu (S) có đường kính AB với A(-2;-4;3), B(4;2;0). Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
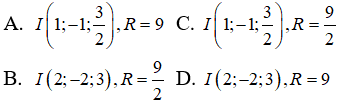
(S) có bán kính:
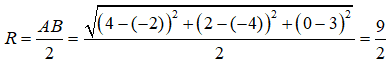
và có tâm I là trung điểm của AB. Ta có:
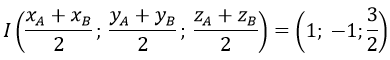
Câu 47: Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:
A. (x - 1)2 + (y + 2)2 + (z + 3)2 = 3 C. (x + 1)2 + (y - 2)2 + (z - 3)2 = 3
B. (x + 1)2 + (y - 2)2 + (z - 3)2 = 9 D. (x - 1)2 + (y + 2)2 + (z + 3)2 = 9
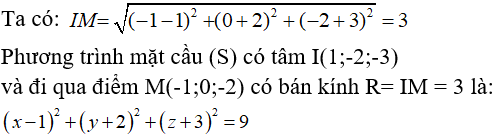
Câu 48: Cho (S) là mặt cầu có tâm I(1;2;4) và đi qua điểm M(-1;4;3). Khẳng định nào dưới đây sai?
A. Bán kính của mặt cầu (S) là R = IM = 3
B. Phương trình chính tắc của mặt cầu (S) là: (x - 1)2 + (y - 2)2 + (z - 4)2 = 9
C. Mặt cầu (S) đi qua gốc tọa độ
D. Phương trình tổng quát của mặt cầu (S) là: x2 + y2 + z2 - 2x - 4y - 8z + 12 = 0
Ta có: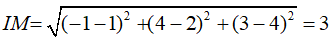 
.
Suy ra:
* Bán kính của mặt cầu (S) là R = IM = 3
* Phương trình chính tắc của mặt cầu (S) là:
(x - 1)2 + (y - 2)2 + (z - 4)2 = 9
* Phương trình tổng quát của mặt cầu (S) là:
x2 + y2 + z2 - 2x - 4y - 8z + 12 = 0
* Thay tọa độ điểm O vào phương trình mặt cầu ta thấy không thỏa mãn nên mặt cầu không đi qua gốc tọa độ O.
Câu 49: Cho mặt cầu (S) có tâm I(1;2;3), bán kính R=4. Khẳng định nào sau đây là sai?
A. Diện tích của mặt cầu (S) bằng 16π
B. Thể tích của khối cầu (S) bằng 64π/3
C. Phương trình chính tắc cúa (S) là: (x + 1)2 + (y + 2)2 + (z + 3)2 = 16
D. Phương trình tổng quát của mặt cầu (S) là: x2 + y2 + z2 - 2x - 4y - 6z - 2 = 0
Câu 50: Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là:
A. (x - 1)2 + (y - 2)2 + (z + 1)2 = 9
C. x2 + y2 + z2 - 2x - 4y + 2z - 3 = 0
B. (x + 1)2 + (y + 2)2 + (z - 1)2 = 9
D. x2 + y2 + z2 = 9
Mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ nên mặt cầu (S’) có tâm I’(-1;-2; 1) đối xứng với I qua gốc O và có bán kính R’ = R = 3.
Phương trình mặt cầu (S’) là:(x + 1)2 + (y + 2)2 + (z - 1)2 = 9
Câu 51: Cho mặt cầu (S) có phương trình: x2 + y2 + z2 - 2x + 4y - 6z - 2 = 0 . Điểm M(m; -2; 3) nằm trong mặt cầu khi và chỉ khi:
A. m=6 B. m > -3 C. -3 < m < 5 D. m < 5
Mặt cầu (S) có tâm I(1;-2;3),
M nằm trong mặt cầu (S) khi và chỉ khi: IM < R nên
Câu 52: Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0;0;1), bán kính R=5. Mặt phẳng (P): 4x - 4y + z + m = 0 cắt mặt cầu (S) theo một đường tròn có bán kính bằng 5. Khi đó m bằng:
A. m=-1 B. m=-4 C. m=3 D. Đáp số khác
Do mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn có bán kính bằng 5 bằng bán kính mặt cầu nên tâm I thuộc mặt phẳng (P) .
Thay tọa độ tâm I vào phương trình mặt phẳng (P) ta được:
4.0- 3.0 + 1+ m= 0 nên m = -1 .
Câu 53: Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(4;0;0), B(0;-2;0), C(0;0;2). Phương trình của mặt cầu (S) là:
A. (x - 1)2 + (y + 1)2 + (z - 1)2 = 6 C. (x - 4)2 + (y + 2)2 + (z + 2)2 = 24
B. (x - 2)2 + (y + 1)2 + (z - 1)2 = 24 D. (x + 2)2 + (y - 1)2 + (z + 1)2 = 6
Gọi I(a; b; c) là tâm của mặt cầu (S). Ta có:
Từ đó: R = OI = √6
Vậy phương trình của mặt cầu (S) là: (x - 2)2 + (y + 1)2 + (z - 1)2 = 6
Câu 54: Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là:
A. x2 + y2 + z2 + 2x - y - 2z = 0 C. x2 + y2 + z2 + 4x - 2y + 4z = 0
B. x2 + y2 + z2 + 4x + 2y - 4z = 0 D. x2 + y2 + z2 + 4x - 2y - 4z = 0
Phương trình tổng quát của mặt cầu (S) có dạng x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 với a2 + b2 + c2 - d > 0
Ta có: O(0; 0; 0) ∈ (S) ⇔ d = 0
A(-4; 0; 0) ∈ (S) ⇔ (-4)2 + 02 + 02 - 2a.(-4) - 0 - 0 + 0 = 0 ⇔ a = -2
B(0; 2; 0) ∈ (S) ⇔ 02 + 22 + 02 - 0 - 2b.2 - 0 + 0 = 0 ⇔ b = 1
C(0; 0; 4) ∈ (S) ⇔ 02 + 02 + 42 - 0 - 0 - 2c.4 - 0 = 0 ⇔ c = 2
Vậy phương trình tổng quát của mặt cầu (S) là: x2 + y2 + z2 + 4x -2y - 4z = 0
Câu 55: Vị trí tương đối của hai mặt cầu (S) có tâm I(1;1;1), bán kính R = 1 và mặt cầu (S’) có tâm I'(3;3;3), bán kính R’=1 là:
A. ở ngoài nhau B. tiếp xúc C. cắt nhau D. chứa nhau
Do đó, hai mặt cầu đã cho ở ngoài nhau.
Câu 56: Vị trí tương đối của hai mặt cầu: x2 + y2 + z2 + 2x - 2y - 2z - 7 = 0 và x2 + y2 + z2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau B. tiếp xúc C. cắt nhau D. chứa nhau
Mặt cầu: x2 + y2 + z2 + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và
Mặt cầu: x2 + y2 + z2 + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1
Do đó, hai mặt cầu này cắt nhau.
Câu 57: Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian tỏa mãn đẳng thức AM2 + 2BM2 = 30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S).
A. I(-1; -1; -4); R = √6 C. I(-1; -1; -4); R = √30/2
B. I(-2; -2; -8); R = 3 D. I(-1; -1; -4); R = 3
Gọi I là trung điểm của AB. AB = √24
Theo công thức đường trung tuyến ta có
Mặt khác ta có 
Nên I(-1; -1; -4) . Từ đó suy ra đáp án đúng là D.
Đáp án A và C sai do nhớ nhầm công thức tính đường trung tuyến
Đáp án B sai do tính nhầm công thức trung điểm
Câu 58: Trong không gian Oxyz, cho hai điểm A(0;2;-4), B(-3;5;2). Tìm tọa độ điểm M sao cho biểu thức AM2 + 2BM2 đạt giá trị nhỏ nhất.
A. M(-3/2; 7/2; -1) B. M(-1; 3; -2) C. M(-2; 4; 0) D. M(-3; 7; -2)
Gọi M(x; y; z). Ta có:
AM2 + 2BM2 = x2 + (y - 2)2 + (z + 4)2 + 2[(x + 3)2 + (y - 5)2 + (z - 2)2]
= x2 + y2- 4y + 4+ z2 +8z+ 16 + 2(x2+ 6x + 9 + y2 – 10y + 25 + z2 – 4z + 4)
= 3(x2 + y2 + z2 + 4x - 8y) + 96 = 3[(x + 2)2 + (y - 4)2 + z2] + 36 ≥ 36
Dấu bằng xảy ra khi và chỉ khi x = -2, y = 4, z = 0 → M(-2; 4; 0) .
Vậy đáp án đúng là C
Dấu bằng xảy ra khi và chỉ khi M trùng I. Từ đó sau khi tìm được điểm I ta suy ra đáp án C đúng.
Nếu đề bài hỏi AM2 + BM2 đạt giá trị nhỏ nhất thì đáp án đúng là A ( vị trí trung điểm của AB)
Câu 59: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: (x - 1)2 + (y - 1)2 + (z - 3)2 = 4
Cho ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện góc AMB = 90o . Diện tích tam giác AMB có giá trị lớn nhất là:
A. 4 B. 2 C. 4π D. Không tồn tại
Ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện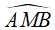 
= 90°
Nên tam giác AMB vuông tại M.
Ta có:
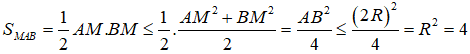
Dấu bằng xáy ra khi và chỉ khi tam giác MAB vuông cân tại M và AB là một đường kính của mặt cầu (S). Vậy đáp án đúng là A.
Câu 60: Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng:
A. 8 B. 2 C. 12 D. 6
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
