Các dạng bài tập trắc nghiệm vận dụng cao nguyên hàm và một số phương pháp tìm nguyên hàm

Quang Trung Ngày: 08-03-2024 Lớp 12

Tải xuống 31 777 4

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các dạng bài tập trắc nghiệm vận dụng cao nguyên hàm và một số phương pháp tìm nguyên hàm, tài liệu bao gồm 31 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Các dạng bài tập trắc nghiệm vận dụng cao nguyên hàm và một số phương pháp tìm nguyên hàm

Chương 3: Nguyên hàm - tích phân và ứng dụng

Bài 1: Nguyên hàm và phương pháp tìm nguyên hàm

A. Kiến thức cơ bản cần nắm

I. Nguyên hàm và tính chất

1. Nguyên hàm

Định nghĩa: Cho hàm số f(x) xác định trên K ( K là khoảng hoặc đoạn hoặc nửa đoạn của \(\mathbb{R}\)). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu \({F^\prime }(x) = f(x)\) với mọi \(x \in K\).

Định lý 1: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

Định lý 2: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) đều có dạng F(x) + C, với C là một hằng số.

Hai định lý trên cho thấy:

Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì \(F(x) + C,C \in \mathbb{R}\) là họ tất cả các nguyên hàm của f(x) trên K. Kí hiệu

\(\int f (x)dx = F(x) + C.\)

Chú ý : Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì \({\rm{dF}}({\rm{x}}) = {{\rm{F}}^\prime }({\rm{x}}){\rm{dx}} = {\rm{f}}({\rm{x}}){\rm{d}}x.\)

2. Tính chất của nguyên hàm

Tính chất 1

\(\int {{f^\prime }} (x)dx = f(x) + C\)

Tính chất 2

\(\int k f(x)dx = k\int f (x)dx,\)k là hằng số khác 0.

Tính chất 3

\[\smallint [{\rm{f}}({\rm{x}}) \pm {\rm{g}}({\rm{x}})]{\rm{dx}} = \smallint {\rm{f}}({\rm{x}}){\rm{dx}} \pm \smallint {\rm{g}}({\rm{x}}){\rm{dx}}\]

3. Sự tồn tại của nguyên hàm

Định lý 3: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

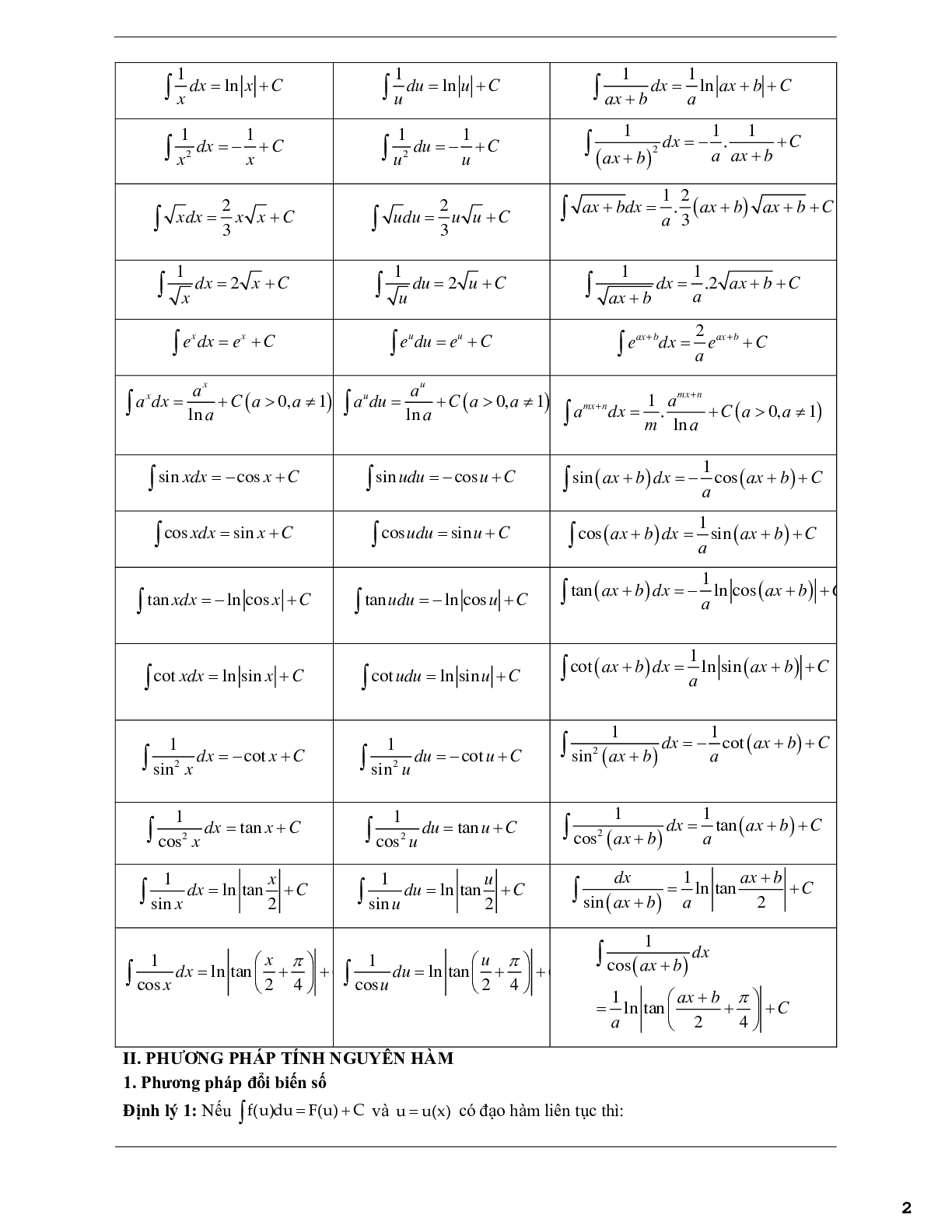
4. Bảng nguyên hàm

Nguyên hàm của hàm số sơ cấp	Nguyên hàm của hàm số hợp (u = u(x))	Nguyên hàm của hàm số hợp (u = ax + b; a≠0)
\(\int d x = x + C\)	\(\int d u = u + C\)	\(\int d (ax + b) = ax + b + C\)
\(\int {{x^\alpha }} dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)\)	\(u = \frac{{{u^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)\)	\(\int {{{(ax + b)}^a}} dx = \frac{1}{a}\frac{{{{(ax + b)}^{n + 1}}}}{{\alpha + 1}} + C(\alpha \ne 0)\)
\(\int {\frac{1}{x}} dx = \ln \|x\| + C\)	\(\int {\frac{1}{u}} du = \ln \|u\| + C\)	\(\int {\frac{1}{{ax + b}}} dx = \frac{1}{a}\ln \|ax + b\| + C\)
\(\int {\frac{1}{{{x^2}}}} dx = - \frac{1}{x} + C\)	\(\int {\frac{1}{{{u^2}}}} du = - \frac{1}{u} + C\)	\(\int {\frac{1}{{{{(ax + b)}^2}}}} dx = - \frac{1}{a} \cdot \frac{1}{{ax + b}} + C\)
\(\int {\sqrt x } dx = \frac{2}{3}x\sqrt x + C\)	\(\int {\sqrt u } du = \frac{2}{3}u\sqrt u + C\)	\(\int {\sqrt {ax + b} } dx = \frac{1}{a} \cdot \frac{2}{3}(ax + b)\sqrt {ax + b} + C\)
\(\int {\frac{1}{{\sqrt x }}} dx = 2\sqrt x + C\)	\(\int {\frac{1}{{\sqrt u }}} du = 2\sqrt u + C\)	\(\int {\frac{1}{{\sqrt {ax + b} }}} dx = \frac{1}{a} \cdot 2\sqrt {ax + b} + C\)
\(\int {{e^x}} dx = {e^x} + C\)	\(\int {{e^n}} du = {e^n} + C\)	\(\int {{e^{ax + b}}} dx = \frac{2}{a}{e^{ax + b}} + C\)
\(\int {{a^x}} dx = \frac{{{a^x}}}{{\ln a}} + C(a > 0,a \ne 1)\)	\(\int {{a^u}} du = \frac{{{a^a}}}{{\ln a}} + C(a > 0,a \ne 1)\)	\(\int {{a^{nux + n}}} dx = \frac{1}{m} \cdot \frac{{{a^{n + n}}}}{{\ln a}} + C(a > 0,a \ne 1)\)
\(\int {\sin } xdx = - \cos x + C\)	\(\int {\sin } udu = - \cos u + C\)	\(\int {\sin } (ax + b)dx = - \frac{1}{a}\cos (ax + b) + C\)
\(\int {\cos } xdx = \sin x + C\)	\(\int {\cos } udu = \sin u + C\)	\(\int {\cos } (ax + b)dx = \frac{1}{a}\sin (ax + b) + C\)
\(\int {\tan } xdx = - \ln \|\cos x\| + C\)	\(\int {\tan } udu = - \ln \|\cos u\| + C\)	\(\int {\tan } (ax + b)dx = - \frac{1}{a}\ln \|\cos (ax + b)\| + \)
\(\int {\cot } xdx = \ln \|\sin x\| + C\)	\(\int {\cot } udu = \ln \|\sin u\| + C\)	\(\int {\cot } (ax + b)dx = \frac{1}{a}\ln \|\sin (ax + b)\| + C\)
\(\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\)	\(\int {\frac{1}{{{{\sin }^2}u}}} du = - \cot u + C\)	\(\int {\frac{1}{{{{\sin }^2}(ax + b)}}} dx = - \frac{1}{a}\cot (ax + b) + C\)
\(\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C\)	\(\int {\frac{1}{{{{\cos }^2}u}}} du = \tan u + C\)	\(\int {\frac{1}{{{{\cos }^2}(ax + b)}}} dx = \frac{1}{a}\tan (ax + b) + C\)
\(\int {\frac{1}{{{{\sin }^x}}}} dx = \ln \left\| {\tan \frac{x}{2}} \right\| + C\)	\(\int {\frac{1}{{{{\sin }^2}u}}} du = \ln \left\| {\tan \frac{u}{2}} \right\| + C\)	\(\int {\frac{{dx}}{{{{\sin }^2}(ax + b)}}} = \frac{1}{a}\ln \left\| {\tan \frac{{ax + b}}{2}} \right\| + C\)
\(\int {\frac{1}{{{{\cos }^2}}}} dx = \ln \left\| {\tan \left( {\frac{x}{2} + \frac{\pi }{4}} \right)} \right\|\)	\(\int {\frac{1}{{{{\cos }^2}}}} du = \ln \left\| {\tan \left( {\frac{u}{2} + \frac{\pi }{4}} \right)} \right\|\)	\(\int {\frac{1}{{\cos (ax + b)}}} dx\)\( = \frac{1}{a}\ln \mid \tan \left( {\frac{{ax + b}}{2} + \frac{\pi }{4}} \right) + C\)

II. Phương pháp tính nguyên hàm

1. Phương pháp đổi biến số

Định lý 1: Nếu \(\int {\rm{f}} ({\rm{u}}){\rm{du}} = {\rm{F}}({\rm{u}}) + {\rm{C}}\) và u = u(x) có đạo hàm liên tục thì:

\(\int f [u(x)] \cdot {u^\prime }(x)dx = F[u(x)] + C\)

Hệ quả: Với \(u = ax + b(a \ne 0)\) ta có

\(\int f (ax + b)dx = \frac{1}{a}F(ax + b) + C.\)

2. Phương pháp tính nguyên hàm từng phần:

Định lý 2: Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:

\(\int u (x){v^\prime }(x)dx = u(x)v(x) - \int {{u^\prime }} (x)v(x)dx.\)

B. Phân loại và phương pháp giải bài tập

Dạng 1: Tìm nguyên hàm bằng các phép biến đổi sơ cấp

1. Phương pháp giải

- Biến đổi các hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x, trong đó mỗi biểu thức chứa x là những dạng cơ bản có trong bảng nguyên hàm.

- Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản để tìm nguyên hàm.

2. Bài tập

Bài tập 1. Nguyên hàm của hàm số \(f(x) = \frac{{{2^x} - 1}}{{{e^x}}}\) là

A. \(\frac{{{2^x}}}{{{e^x}\ln 2}} + {e^{ - x}} + C\)

B. \(\frac{{{2^x}}}{{{e^x}(\ln 2 - 1)}} - {e^{ - x}} + C\)

C. \(\frac{{{2^x}}}{{{e^x}(\ln 2 - 1)}} + {e^{ - x}} + C\)

D. \(\frac{{{2^x}}}{{{e^x}(\ln 2 - 1)}} + {e^x} + C\)

Hướng dẫn giải

Chọn C.

Ta có:

\(\begin{array}{l}\int {\frac{{{2^x} - 1}}{{{e^x}}}} dx = \int {{{\left( {\frac{2}{e}} \right)}^x}} dx - \int {{e^{ - x}}} dx\\ = \frac{{{2^x}}}{{{e^x}(\ln 2 - 1)}} + {e^{ - x}} + C\end{array}\).

Bài tập 2. Nguyên hàm của hàm số \(f(x) = x{(x + 2)^{2019}}\) là

A. \( - \frac{{{{(x + 2)}^{2021}}}}{{2021}} - \frac{{{{(x + 2)}^{2020}}}}{{1010}} + C\)

B. \(\frac{{{{(x + 2)}^{2020}}}}{{2021}} - \frac{{{{(x + 2)}^{2018}}}}{{1009}} + C\)

C. \(\frac{{{{(x + 2)}^{2021}}}}{{2021}} + \frac{{{{(x + 2)}^{2020}}}}{{1010}} + C\)

D. \(\frac{{{{(x + 2)}^{2021}}}}{{2021}} - \frac{{{{(x + 2)}^{2020}}}}{{1010}} + C\)

Hướng dẫn giải

Chọn D.

Ta có: \[\int {x{{(x + 2)}^{2019}}dx = } \int {\left[ {(x + 2) - 2} \right]} {(x + 2)^{2019}}(dx\]

\(\begin{array}{l} = \int {{{(x + 2)}^{2020}}} dx - 2\int {{{(x + 2)}^{2019}}} dx\\ = \frac{{{{(x + 2)}^{2021}}}}{{2021}} - \frac{{{{(x + 2)}^{2020}}}}{{1010}} + C\end{array}\)

Bài tập 3. Nguyên hàm của hàm số \(f(x) = \frac{1}{{{e^{2x}} + 1}}\) là

A. \(x + \ln \sqrt {{e^{2x}} + 1} + C\)

B. \(x - \frac{1}{2}\ln \left( {{e^{2x}} + 1} \right) + C\)

C. \(\ln \left( {{e^{2x}} + 1} \right) + C\)

D. \(x - \ln \left( {{e^{2x}} + 1} \right) + C\)

Hướng dẫn giải

Chọn B.

Ta có: \(\frac{1}{{{e^{2x}} + 1}} = \frac{{\left( {{e^{2x}} + 1} \right) - {e^{2x}}}}{{{e^{2x}} + 1}} = 1 - \frac{{{e^{2x}}}}{{{e^{2x}} + 1}}.\)

Do đó

\(\begin{array}{l}\int {\frac{1}{{{e^{2x}} + 1}}} dx = \int {\left( {1 - \frac{{{e^{2x}}}}{{{e^{2x}} + 1}}} \right)} dx\\ = \int d x - \frac{1}{2}\int {\frac{{d\left( {{e^{2x}} + 1} \right)}}{{{e^{2x}} + 1}}} \\ = x - \frac{1}{2}\ln \left( {{e^{2x}} + 1} \right) + C\end{array}\)

Bài tập 4. Nguyên hàm của hàm số \(f(x) = \frac{1}{{\sqrt {x + 2} + \sqrt {x - 2} }}\) là:

A. \(\frac{1}{6}\left[ {{{(\sqrt {x + 2} )}^3} - {{(\sqrt {x - 2} )}^3}} \right] + C\)

B. \(\frac{1}{6}[\sqrt {x + 2} - \sqrt {x - 2} ] + C\)

C. \(\frac{1}{6}\sqrt {x + 2} + \frac{1}{6}(x - 2)\sqrt {x - 2} + C\)

D. \(\frac{1}{6}(x + 2)\sqrt {x + 2} - \frac{1}{6}\sqrt {x - 2} + C\)

Hướng dẫn giải

Chọn A.

Ta có: \(\int {\frac{1}{{\sqrt {x + 2} + \sqrt {x - 2} }}} dx = \int {\frac{{\sqrt {x + 2} - \sqrt {x - 2} }}{4}} dx\)

\(\begin{array}{l} = \frac{1}{4}\left[ {\frac{2}{3}(x + 2)\sqrt {x + 2} - \frac{2}{3}(x - 2)\sqrt {x - 2} } \right] + C\\ = \frac{1}{6}(x + 2)\sqrt {x + 2} - \frac{1}{6}(x - 2)\sqrt {x - 2} + C\end{array}\)

Chú ý: Sử dụng kĩ thuật nhân liên hợp: \(\sqrt a \pm \sqrt b = \frac{{a - b}}{{\sqrt a \mp \sqrt b }}\).

Lưu ý: \(\int {\sqrt {ax + b} } dx = \frac{2}{{3a}}(ax + b)\sqrt {ax + b} + C\).

Bài tập 5. Nguyên hàm của hàm số \(f(x) = \frac{{5x - 13}}{{{x^2} - 5x + 6}}\) là:

A. \(2\ln |x - 3| - 3\ln |x + 2| + C\)

B. \(3\ln |x - 3| + 2\ln |x - 2| + C\)

C. \(2\ln |x + 3| + 3\ln |x + 2| + C\)

D. \(2\ln |x - 3| + 3\ln |x - 2| + C\)

Hướng dẫn giải

Chọn D.

Ta có: \(\frac{{5x - 13}}{{{x^2} - 5x + 6}} = \frac{{5x - 13}}{{(x - 2)(x - 3)}}\)

Ta sẽ phân tích: \(5x - 13 = A(x - 2) + B(x - 3)\) (1)

Thế x = 2 và x = 3 lần lượt vào (1) ta có B = 3 và A = 2.

Khi đó

\(\begin{array}{l}\int {\frac{{5x - 13}}{{{x^2} - 5x + 6}}} dx = \int {\frac{{2(x - 2) + 3(x - 3)}}{{(x - 2)(x - 3)}}} dx\\ = \int {\frac{2}{{x - 3}}} dx + \int {\frac{3}{{x - 2}}} dx\end{array}\)

\( = 2\ln |x - 3| + 3\ln |x - 2| + C\)

Bài tập 6. Nguyên hàm của hàm số \(f(x) = \frac{{1 - {x^4}}}{{{x^5} + x}}\) là:

A. \(\ln |x| + \frac{1}{2}\ln \left( {{x^4} + 1} \right) + C\)

B. \(\ln |x| - \ln \left( {{x^4} + 1} \right) + C\)

C. \(\ln |x| - \frac{1}{2}\ln \left( {{x^4} + 1} \right) + C\)

D. \(\ln |x| - \frac{1}{2}\ln \left( {{x^4} + 1} \right) + C\)

Hướng dẫn giải

Chọn C.

Ta có:

\[\begin{array}{l}\int {\frac{{1 - {x^4}}}{{{x^5} + x}}} dx = \int {\frac{{\left( {1 + {x^4}} \right) - 2{x^4}}}{{x\left( {{x^4} + 1} \right)}}} dx\\ = \int {\frac{1}{x}} dx - \int {\frac{{2{x^3}}}{{{x^4} + 1}}} dx\\ = \ln |x| - \frac{1}{2}\ln \left( {{x^4} + 1} \right) + C\end{array}\]

Bài tập 7. Nguyên hàm của hàm số \(f(x) = \frac{{3{x^2} + 3x + 3}}{{{x^3} - 3x + 2}}\) là:

A. \(\ln |x + 2| + 2\ln |x - 1| - \frac{3}{{x - 1}} + C\)

B. \(\ln |x + 2| - 2\ln |x - 1| + \frac{3}{{x - 1}} + C\)

C. \(2\ln |x + 2| + \ln |x - 1| - \frac{3}{{x - 1}} + C\)

D. \(2\ln |x + 2| + \ln |x - 1| + \frac{3}{{x - 1}} + C\)

Hướng dẫn giải

Chọn A.

Ta có: \(\int {\frac{{3{x^2} + 3x + 3}}{{{x^3} - 3x + 2}}} dx = \int {\frac{{3{x^2} + 3x + 3}}{{{{(x - 1)}^2}(x + 2)}}} dx\).

Ta phân tích \(3{x^2} + 3x + 3 = A{(x - 1)^2} + B(x - 1)(x + 2) + C(x + 2)\).

Ta có thể dùng các giá trị riêng, tính ngay A = 1; C = 3 và B = 2.

(thay \(x = - 2 \Rightarrow A = 1;x = 1 \Rightarrow C = 3\) và \(x = 0 \Rightarrow B = 2\) ).

Khi đó

\(\begin{array}{l}\int {\frac{{3{x^2} + 3x + 3}}{{{{(x - 1)}^2}(x + 2)}}} dx = \int {\frac{1}{{x + 2}}} dx + 2\int {\frac{1}{{x - 1}}} dx + 3\int {\frac{1}{{{{(x - 1)}^2}}}} dx\\ = \ln |x + 2| + 2\ln |x - 1| - \frac{3}{{x - 1}} + C\end{array}\).

Xem thêm