Tổng hợp các dạng toán thường gặp về Thể tích của hình hộp chữ nhật có lời giải

Quý Lê Xuân Ngày: 08-03-2024 Lớp 8

Tải xuống 11 2.6 K 15

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Thể tích của hình hộp chữ nhật Toán lớp 8, tài liệu bao gồm 11 trang, tuyển chọn bài tập Thể tích của hình hộp chữ nhật đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Thể tích của hình hộp chữ nhật gồm các nội dung chính sau:

A. Lý thuyết

- tóm tắt lý thuyết ngắn gọn và 4 ví dụ mịnh họa có đáp án và lời giải chi tiết.

B. Các dạng bài tập

- gồm 2 dạng bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Thể tích của hình hộp chữ nhật.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Thể tích của hình hộp chữ nhật (ảnh 1)

THỂ TÍCH CỦA HÌNH HỘP CHỮ NHẬT

A. Lý thuyết

1. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG, HAI MẶT PHẲNG VUÔNG GÓC.

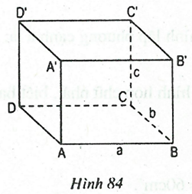
Ví dụ 1: Quan sát hình hộp chữ nhật ở hình 84:

- $A^{'} A$ có vuông góc với AD hay không? Vì sao?

- $A^{'} A$ có vuông góc với AB hay không? Vì sao?

Giải

Ta lần lượt có:

- $A^{'} A$ có vuông góc với AD, bởi $A D D^{'} A^{'}$ là hình chữ nhật.

- $A^{'} A$ có vuông góc với AB, bởi $A B B^{'} A^{'}$ là hình chữ nhật.

Tổng kết và mở rộng:

1. Khi đường thẳng $A^{'} A$ vuông góc với hai đường thẳng cắt nhau AD và AB trong mặt phẳng $(A B C D)$ ta nói $A^{'} A$ vuông góc với mặt phẳng $(A B C D)$ và kí hiệu $A A^{'} ⊥ (A B C D)$ .

2. Khi một trong hai mặt phẳng chứa một đường thẳng vuông góc với mặt phẳng còn lại thì người ta nói hai mặt phẳng đó vuông góc với nhau, ví dụ $(A A^{'} B^{'} B) ⊥ (A B C D)$ bởi mặt phẳng $(A A^{'} B^{'} B)$ chứa đường thẳng $A A^{'}$ vuông góc với $(A B C D)$ .

Nhận xét: Nếu một đường thẳng vuông góc với một mặt phẳng tại điểm A thì nó vuông góc với mọi đường thẳng đi qua A và nằm trong mặt phẳng đó.

Ví dụ 2: Tìm trên hình 84:

- Các đường thẳng vuông góc với mặt phẳng $(A B C D)$ .

- Các mặt phẳng vuông góc với mặt phẳng $(A^{'} B^{'} C^{'} D^{'})$ .

Giải

Ta lần lượt có:

- Các đường thẳng $A^{'} A$ , $B^{'} B$ , $C^{'} C$ , $D^{'} D$ vuông góc với mặt phẳng $(A B C D)$ .

- Các mặt phẳng $(A^{'} A B B^{'})$ , $(B^{'} B C C^{'})$ , $(C^{'} C D D^{'})$ , $(D^{'} D A A^{'})$ vuông góc với mặt phẳng $(A^{'} B^{'} C^{'} D^{'})$ .

2. CÔNG THỨC TÍNH DIỆN TÍCH, THỂ TÍCH CỦA HÌNH HỘP CHỮ NHẬT.

Với hình hộp chữ nhật có ba kích thước a, b, c ta có:

Diện tích xung quanh:

. $S_{x q} = 2 (a + b) c$

Diện tích toàn phần:

$S_{t p} = S_{x q} + 2 S_{d} = 2 (a + b) c + 2 a b = 2 (a c + b c + a b)$ .

Thể tích:

$V = a b c$ .

Đặc biệt: Thể tích của hình lập phương cạnh a là:

$V = a^{3}$ .

Ví dụ 3: Tính thể tích của hình hộp chữ nhật biết ba kích thước bằng 3cm, 4cm, 5cm.

Giải

Ta có ngay: $V = 3.4.5 = 60 c m^{3}$ .

Ví dụ 4: Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ . Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lập phương đó, biết: