Tailieumoi.vn xin giới thiệu đến các quý thầy cô Giáo án Đại số 9 chương 4 bài 4: Công thức nghiệm của phương trình bậc hai mới nhất theo mẫu Giáo án môn Toán học chuẩn của Bộ Giáo dục. Hi vọng tài liệu này sẽ giúp thầy/cô dễ dàng biên soạn chi tiết Giáo án môn Toán học lớp 9. Chúng tôi rất mong sẽ được thầy/cô đón nhận và đóng góp những ý kiến quý báu của mình.
Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Giáo án Toán 9 Bài 4: Công thức nghiệm của phương trình bậc hai
Qua bài này HS cần:
1. Kiến thức:
+ Nhớ biệt số Δ = b2 - 4ac. Với điều kiện nào của Δ thì phương trình vô nghiệm, có nghiệm kép, có hai nghiệm phân biệt.
+ Vận dụng được công thức nghiệm của phương trình bậc hai để giải thành thạo phương trình bậc hai.
2. Kĩ năng:
- Viết được biệt số Δ = b2 - 4ac. Thực hiện được việc giải phương trình bậc hai một ẩn nhờ sử dụng biệt số.
3. Thái độ:
- Nghiêm túc và hứng thú học tập.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán, giải quyết vấn đề, hợp tác, giao tiếp, tự học.
- Phẩm chất: Tự tin, tự chủ
- Gv : Phấn mầu, bảng phụ, thước thẳng
- Hs: Đồ dùng học tập, đọc trước bài.
1. Ổn định :(1 phút)
2. Bài mới :
Hoạt động 1: Khởi động
* GV gọi HS lên bảng làm Ở dưới lớp các em làm vào vở nháp
Giải phương trình: 3x² + 5x + 2 = 0
HS: Ta có:
3x² + 5x + 2 = 0
<=> 3x2 + 3x + 2x + 2 = 0
<=> 3x(x + 1) + 2(x + 1) = 0
<=> (x + 1)(3x + 2) = 0
* Hãy biến đổi phương trình bậc hai đầy đủ sau: ax2 + bx + c = 0 thành phương trình có vế trái là một bình phương, còn vế phải là một hằng số.
Ta có: ax² + bx + c = 0 (a ≠ 0)
GV: Để giải pt bậc hai ta cần có công thức nào ? Chúng ta nghiên cứu bài mới.
Hoạt động 2: Hình thành kiến thức
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
+ Qua kết quả kiểm tra bài cũ của HS 2, hãy cho biết nếu đặt thì ta suy ra được điều gì? + Giải thích về và nêu cho HS cách đọc: là chữ cái Hi Lạp, đọc là:”đen ta” + Người ta ký hiệu và gọi là biệt thức của phương trình. + Xét xem có những trường hợp nào? + GV chia lớp thành 4 nhóm, Yêu cầu HS hoạt động nhóm trong 5 phút điền tieepsvaof chỗ (...) của ?1để hoàn thành công thức nghiệm của pt ứng vơí mỗi trường hợp của + ?Vì sao < 0 thì phương trình vô nghiệm. +Gv giải thích rõ cho hs trường hợp pt có ngh kép và pt vô ngh. Gọi HS nhận xét bài làm của bạn GV nhận xét và nhấn mạnh về công thức nghiệm của phương trình bậc hai. Từ đó yêu cầu HS nhận xét chung ? Qua kết quả trên ta thấy yếu tố nào quyết định sự có nghiệm hay vô nghiệm của phương trình ( Dấu của ) Vậy để giải phương trình bậc hai bằng công thức nghiệm ta cần thực hiện những bước nào? Cho HS làm ví dụ mẫu Hướng dẫn HS làm theo từng bước để giải phương trình bậc hai Cho HS làm ?3/45 Gọi ba HS lên bảng làm bài Theo dõi việc làm bài dưới lớp của HS để hướng dẫn HS yếu và trung bình Gọi HS nhận xét bài làm của bạn ?Nếu a, c trái dấu thì sao? ? Khi đó dấu của như thế nào ? Vậy có thể nói thêm gì về ngh của pt trong trường hợp ac<0 Gv giới thiệu chú ý. |
+ Ta được:
Vế trái của pt (3) là số không âm, vế phải có mẫu dương (4a²>0 vì a ≠ 0) còn tử thức là Δ có thể dương, âm, bằng 0. + HS hoạt động nhóm trong 5 phút sau đó đại diện nhóm trình bày, sau đó nhận xét. Nếu Δ < 0 thì vế trái của phương trình (2) là số không âm còn vế phải là số âm nên phương trình (2) vô nghiệm suy ra phương trình (1) vô nghiệm HS nhận xét bài làm của bạn HS nêu nhận xét của mình về nghiệm của phương trình bậc hai Cho một vài HS đọc to HS có thể không trả lời được Các bước giải phương trình bậc hai một ẩn là: + Bước 1: Xác định các hệ số a, b, c + Bước 2: Tính Δ +Bước 3: Kết luận số ngh của pt dựa vào dấu của Δ. + Bước 4: Tính nghiệm theo công thức nếu pt có ngh. HS theo dõi làm ví dụ mẫu HS cả lớp làm ?3 vào vở của mình Ba HS lên bảng làm bài HS nhận xét bài làm của bạn Nếu a và c trái dấu thì tích a.c < 0 => -4ac>0, khi đó Δ >0 nên pt có hai nghiệm phân biệt phần nhận xét. |
1. Công thức nghiệm Đối với phương trình: ax² + bx + c = 0 (a ≠ 0) (1) và biệt thức Δ = b² -4ac; (2) <=> + Nếu Δ >0
Do đó phương trình (1) có hai nghiệm + Nếu Do đó phương trình (1) có nghiệm kép ?2/44. Nếu Δ <0 => pt vô nghiệm Kết luận chung: SGK/44 2. Áp dụng Ví dụ: Giải phương trình: 3x²+5x+2=0 Hệ số: a=3; b=5; c= 2 Δ =5²–4.3.2=1 Do Δ >0 nên phương trình có hai nghiệm:
?3/45 a/ Hệ số: a=5; b= –1; c=2 Δ =(–1)²–4.5.2= –39<0 Vậy phương trình vô nghiệm b/ Hệ số: a=4; b= –4; c=1 Δ =(–4)²–4.4.1=0 P.trình có nghiệm kép: x=1/2 c/ Hệ số: a= –3; b=1; c=5 Δ =1²–4.(–3).5=0 Vậy phương trình có 2 ngh:
• Chú ý: Xem SGK/445 |
Hoạt động 3: Luyện tập
Mục tiêu: HS vận dụng thành thạo công thức nghiệm giải pt bậc hai
PP: Hoạt động nhóm, thuyết trình
Làm bài tập 16 a,b,c,d: (1 nửa lớp làm câu a,c; 1 nửa lớp làm câu c,d)
Dùng công thức nghiệm để giải các pt sau:
HS hoạt động nhóm, trình bày ra giấy, 2 nhóm ghi KQ vào bảng phụ
GV yêu cầu đại diện nhóm trình bày kết quả.
HS quan sát, nhận xét
Hoạt động 4: Vận dụng
Cho pt: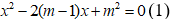 
(1)
a) Giải pt với m = -1
b) Tìm m để pt có nghiệm kép? pt có hai nghiệm phân biệt?
Hoạt động 5: Tìm tòi, mở rộng
Bài tập về nhà: 15,16/45 SGK và bài 15, 16, 20, 21 SBT.
Đọc phần có thể em chưa biết và bài đọc thêm trong SGK/46,47
Học thuộc công thức nghiệm của phương trình bậc hai
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
; 
