Tailieumoi.vn xin giới thiệu chuyên đề Phép quay thuộc chương trình Toán 11. Chuyên đề gồm 16 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.

Chuyên đề Phép quay

Phần 1: Dạng bài tập về phép quay 90 độ cực hay

A. Phương pháp giải

[1]. Biểu thức tọa độ của phép quay 90° và -90°

Trong hệ trục tọa Oxy:

[2]. Bài toán xác định vị trí của điểm, hình khi thực hiện phép quay cho trước

Bước 1. Xác định tâm quay và góc quay theo yêu cầu bài toán.

Bước 2. Áp dụng các kiến thức sau:

Bước 3. Kết luận.

B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC, trọng tâm G ( thứ tự các điểm như hình vẽ)

a) Tìm ảnh của điểm B qua phép quay tâm A góc quay 90°

b) Tìm ảnh của đường thẳng BC qua phép quay tâm A góc quay 90°

c) Tìm ảnh của tam giác ABC qua phép quay tâm G góc quay 90°

Hướng dẫn giải:

a)

Dựng đoạn thẳng AB’ bằng đoạn thẳng AB sao cho 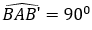 (Vị trí B’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)

• Khi đó: 

• Vậy B’ à ảnh của điểm B qua phép quay tâm A, góc quay 90°

b)

• Dựng đoạn thẳng AC’ bằng đoạn thẳng AC sao cho 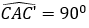 (Vị trí C’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)

• 

Mặt khác, Q_(A,90°)(B) = B' (theo câu a) (2)

• Từ (1) và (2) suy ra: Q_(A,90°)(BC) = B'C'

c)

• Dựng đoạn thẳng GA’ bằng đoạn thẳng GA sao cho 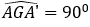 (Vị trí A’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)

• Dựng đoạn thẳng GB’’ bằng đoạn thẳng GB sao cho 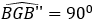 (Vị trí B’’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)

• Dựng đoạn thẳng GC’’ bằng đoạn thẳng GC sao cho 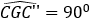 (Vị trí C’’ như hình vẽ sao để chiều quay dương và có độ lớn góc quay bằng 90°)

• Khi đó:

Từ (1),(2),(3) suy ra: Q_(G,90°)(ΔABB) = ΔAB''C''

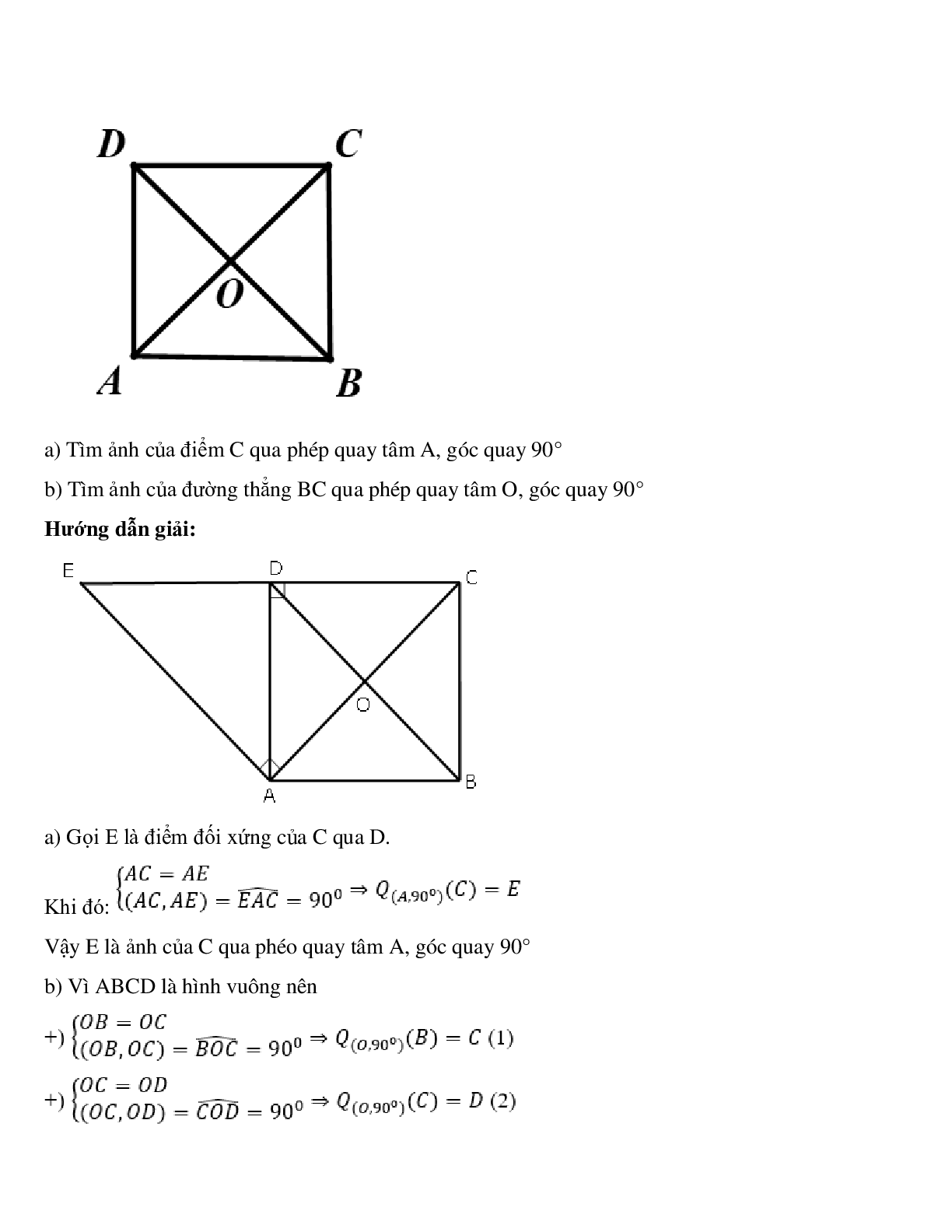
Ví dụ 2: Cho hình vuông ABCD tâm O ( thứ tự các điểm như hình vẽ)

a) Tìm ảnh của điểm C qua phép quay tâm A, góc quay 90°

b) Tìm ảnh của đường thẳng BC qua phép quay tâm O, góc quay 90°

Hướng dẫn giải:

a) Gọi E là điểm đối xứng của C qua D.

Khi đó: 

Vậy E là ảnh của C qua phéo quay tâm A, góc quay 90°

b) Vì ABCD là hình vuông nên

Từ (1) và (2) suy ra: Q_(O,90°)(BC) = CD

Vậy CD là ảnh của BC qua phép quay tâm O góc quay 90°

Ví dụ 3: Trong mặt phẳng tọa độ Oxy cho điểm A(-1;5); đường thẳng d: 3x - y + 2 = 0 và đường tròn (C): (x + 4)² + (y - 1)² = 16

a) Tìm tọa độ điểm B là ảnh của điểm A qua phép quay tâm O(0;0) góc quay -90°.

b) Viết phương trình đường thẳng d' là ảnh của d qua phép quay tâm O góc quay -90°.

c) Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay -90°

Hướng dẫn giải:

a)

Cách 1:

+) Do Q_(O,90°)(A) = B nên dựa vào vẽ bên ta suy ra: B(5;1).

Cách 2:

+) Do Q_(O,90°)(A) = B nên .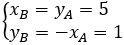

Vậy B(5;1).

b) Qua phép quay tâm O góc quay -90° đường thẳng d biến thành đường thẳng d' vuông góc với d.

Phương trình đường thẳng d' có dạng: x + 3y + m = 0.

Lấy A(0;2) ∈ d. Qua phép quay tâm O góc quay -90°, điểm A(0;2) biến thành điểm B(2;0) ∈ d'. Khi đó m = -2.

Vậy phương trình đường d' là x + 3y - 2 = 0.

c) Từ (C), ta có tâm I(-4; 1) và bán kính R = 4.

Khi đó: Q_(O,90°)(I) = I'(1;4) và bán kính R' = R = 4.

Vậy: Q_(O,90°)(C) = (C'): (x - 1)² + (y - 4)² = 16

Phần 2: Dạng bài tập về phép quay 180 độ cực hay

A. Phương pháp giải

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng Oxy, cho các điểm A(1;2) và B(-3;4). Tìm ảnh của điểm A và B qua phép Quay tâm O góc quay 180°

Hướng dẫn giải:

● Gọi A’ là ảnh của điểm A qua phép quay tâm O góc quay 180°. Khi đó: A’( -1;-2)

● Gọi B’ là ảnh của điểm B qua phép quay tâm O góc quay 180°. Khi đó: B’( 3;-4)

Ví dụ 2: Trong mặt phẳng Oxy, cho đường thắng d: 2x - 5y + 3 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép quay tâm O, góc quay 180°.

Hướng dẫn giải:

Cách 1:

+) Do Q_(0,180°)(d) = d' nên d'//d. Do đó d' có PT dạng: 2x - 5y + m = 0 (m ≠ 3).

+) Chọn M(1;1) ∈ d, gọi M'(x';y') ∈ d' là ảnh của điểm M qua phép quay Q_(0,180°).

Suy ra: 

+) Do M'(-1;-1) ∈ d' nên 2.(-1) - 5.(-1) + m = 0 ⇔ m = -3.

+) Vậy d' có PT là 2x - 5y - 3 = 0.

Cách 2:

+) Với mọi điểm M(x;y) ∈ d, M'(x';y') ∈ d' sao cho A.

+) Khi đó ta có: 

+) Do M(x;y) ∈ d nên ta có 2x - 5y + 3 = 0 ⇔ -2x' + 5y' + 3 = 0 ⇔ 2x' - 5y' - 3 = 0.

+) Do M'(x';y') ∈ d' nên d' có PT là 2x - 5y - 3 = 0.

Cách 3:

Chú ý công thức nhanh: Trong mp Oxy, cho d: Ax + By + C = 0.

Nếu Q_(O,α)(d) = d' và α = π + k2π, O ∉ d thì d' có PT là: Ax + By - C = 0.

+) Do d: 2x - 5y + 3 = 0 và Q_(O,180°)(d) = d' nên d' có PT là 2x - 5y - 3 = 0.

Ví dụ 3: Trong mặt phẳng Oxy, cho đường tròn (C): (x - 2)² + (y + 3)² = 9. Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay 180°.

Hướng dẫn giải:

Cách 1:

+) Đường tròn (C) có tâm I(2;-3) và bán kính R = 3.

+ Gọi C'(I',R') là ảnh của (C) qua phép quay Q_(0,180°).

Khi đó ta có: R' = R = 3 và Q_(0,180°)(I) = I', suy ra: 

+) Vậy (C') có PT là: (x + 2)² + (y - 3)² = 9.

Cách 2:

+ Gọi (C') là ảnh của (C) qua phép quay Q_(0,180°).

+) Với mọi điểm M(x;y) ∈ (C), M'(x';y') ∈ (C') sao cho Q_(0,180°)(M) = M'.

+) Khi đó ta có: 

+) Do M(x;y) ∈ (C) nên ta có: (x - 2)² + (y + 3)² = 9 ⇔ (-x' - 2)² + (-y' + 3)² = 9 ⇔ (x' + 2)² + (y' - 3)² = 9

+) Do M'(x';y') ∈ (C') nên (C') có PT là (x + 2)² + (y - 3)² = 9.

Chú ý: Ưu tiên giải cách 1.

Cách 3:

Chú ý công thức nhanh: Trong mpOxy, cho (C): (x - A)² + (y - B)² = R².

Nếu Q_((O,α)) ((C)) = (C') và α = π + k2π thì (C'): (x + A)² + (y + B)² = R².

+) Do (C): (x - 2)² + (y + 3)² = 9 và Q_(0,180°)((C)) = (C') nên (C') có PT là: (x + 2)² + (y - 3)² = 9.

Phần 3: Cách tìm ảnh của điểm qua phép quay cực hay

A. Phương pháp giải

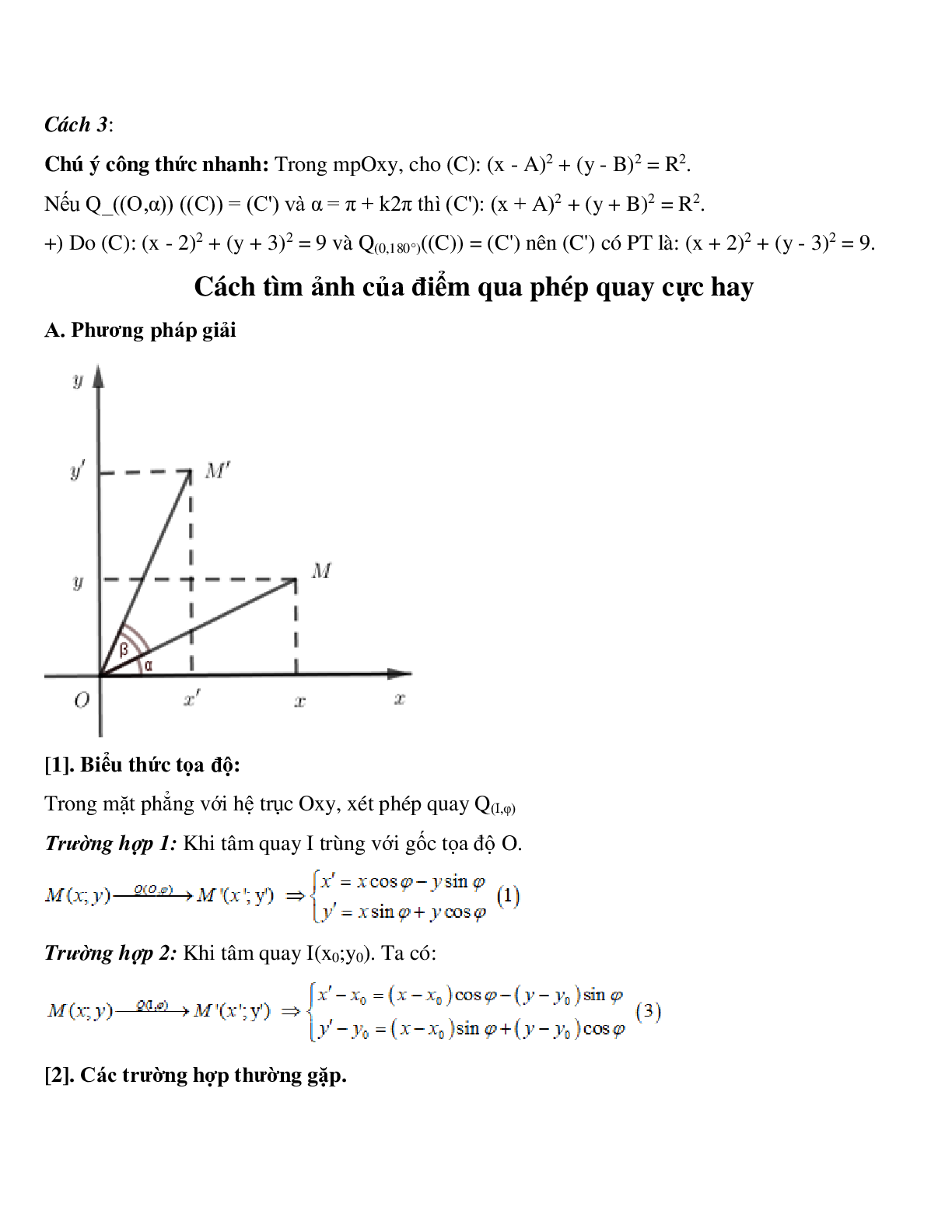
[1]. Biểu thức tọa độ:

Trong mặt phẳng với hệ trục Oxy, xét phép quay Q_(I,φ)

Trường hợp 1: Khi tâm quay I trùng với gốc tọa độ O.

Trường hợp 2: Khi tâm quay I(x₀;y₀). Ta có:

[2]. Các trường hợp thường gặp.

B. Ví dụ minh họa

Ví dụ 1: Tìm ảnh của các điểm sau qua phép quay tâm O, góc 90°, biết:

a) A(3; -4)

b) B(-2; 1)

c) C(4; 5)

d) D(-2; -3)

e) E(0; -5)

Hướng dẫn giải:

Ví dụ 2: Tìm ảnh của các điểm sau qua phép quay tâm O, góc -90°, biết:

a) A(2; 5)

b) B(-4; 2)

c) C(-3; -1)

Hướng dẫn giải:

Ví dụ 3: Tìm tọa độ của điểm A sao cho 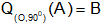, biết:

a) B(3; -5)

b) B(-2; 7)

c) B(-3; -1)

d) B(4; 6)

Hướng dẫn giải:

Ví dụ 4: Tìm ảnh của các điểm sau qua phép quay tâm O, góc 180°, biết:

a) A(-5; 1)

b) B(-4; -7)

c) C(2; 3)

d) D(4; -8)

Hướng dẫn giải:

Phần 4: Cách tìm ảnh của đường thẳng qua phép quay cực hay

A. Phương pháp giải

● Cho đường thẳng Δ:ax+by+c = 0

Cách 1: Sử sụng tính chất hai đường thẳng vuông góc ( nêu ở trên)

Cách 2: Sử dụng phương pháp quý tích, với các lưu ý dưới đây:

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, tìm ảnh của đường thẳng d: 6x - 5y + 18 = 0 qua phép quay Q_(O,90°).

Hướng dẫn giải:

Cách 1.

d'⊥d nên phương trình có dạng 5x + 6y + c = 0

Lấy M(-3;0) ∈ d, ta có Q_(O,90°)(M) = M'(0;-3), M' ∈ d' ⇒ c = 18, hay d': 5x + 6y + 18 = 0.

Cách 2.

Ta có phương trình d:6x - 5y + 18 = 0

Gọi d’ là ảnh của d qua Q_(O,90°). Khi đó với M(x;y) ∈ d ⇒ M'(x';y'⁡) ∈ d'

Thay (*) vào phương trình của d ta được: d: 6y' - 5(-x') + 18 = 0 ⇔ d': 5x + 6y + 18 = 0

Vậy: d': 5x + 6y + 18 = 0.

Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x - y + 3 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép quay tâm O góc quay -90°.

Hướng dẫn giải:

Cách 1. Qua phép quay tâm O góc quay -90° đường thẳng d biến thành đường thẳng d' vuông góc với d.

Phương trình đường thẳng d' có dạng: x + 2y + c = 0.

Lấy A(0;3) ∈ d. Qua phép quay tâm O góc quay -90°, điểm A(0;3) biến thành điểm B(3;0) ∈ d'. Khi đó c = -3.

Vậy phương trình đường d' là x + 2y - 3 = 0.

Cách 2. Ta có phương trình d: 2x - y + 3 = 0

Gọi d’ là ảnh của d qua Q_(O,-90°). Khi đó với M(x;y) ∈ d ⇒ M'(x';y'⁡) ∈ d'

Thay (*) vào phương trình của d ta được: 2(-y') - x + 3 = 0 ⇔ d': x' + 2y' - 3 = 0

Vậy: d': x + 2y - 3 = 0.

Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + 2y - 5 = 0 , điểm I(3;1), phép quay Q_(I,90°)(d) = d'. Xác định phương trình đường thẳng d'.

Hướng dẫn giải:

Ta có: I ∈ d ⇒ I ∈ d'

Đường thẳng d' có dạng: 2x - y + c = 0.

Vì d' đi qua Inên 2.3 - 1 + c = 0 ⇒ c = -5 ⇒ d': 2x - y - 5 = 0

Phần 5: Cách tìm ảnh của đường tròn qua phép quay cực hay

A. Phương pháp giải

Cách 1: Dựa vào tính chất của phép quay.

Cho đường tròn C(A;R) và Q_(I,α)((C)) = (C'), với C'(A';R').

Khi đó ta có:

 i) R' = R.

 ii) Q_(I,α)(A) = A' (quay về dạng toán tìm tọa độ điểm)

Cách 2: Dựa vào biểu thức toạ độ (Phương pháp quỹ tích)

B. Ví dụ minh họa

Ví dụ 1: Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay -90° biết: (C): (x + 4)² + (y - 1)² = 16

Hướng dẫn giải:

Từ (C), ta có tâm I(-4; 1) và bán kính R = 4. Khi đó: Q_(O,-90°)(I) = I'(1;4) và bán kính R'=R = 4

Vậy: Q_(O,-90°)(C) = (C'): (x - 1)² + (y - 4)² = 16

Ví dụ 2: Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay 90° biết: (C): (x + 3)² + (y - 2)² = 25

Hướng dẫn giải:

Từ (C), ta có tâm I(-3; 2) và bán kính R = 5. Khi đó: Q_(O,-90°)(I) = I'(-2;-3) và bán kính R' = R = 5

Vậy: Q_(O,-90°)(C) = (C'): (x + 2)² + (y + 3)² = 25

Ví dụ 3: Tìm ảnh của các đường tròn (C): (x + 1)² + (y - 1)² = 9 qua phép quay tâm O góc 90°

Hướng dẫn giải:

Ta có: (x + 1)² + (y - 1)² = 9 có tâm I(-1;1) bán kính r = 3

Gọi I' là ảnh của tâm I qua Q_(O,90°) ⇒ I'(-1;-1)

Suy ra ảnh của đường tròn qua phép quay trên là (x + 1)² + (y + 1)² = 9.

Phép quay

1. Định nghĩa

Cho điểm O và góc lượng giác $\alpha$ Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M' sao cho  OM'=OM

và góc lượng (OM;OM') bằng $\alpha$ được gọi là phép quay tâm O góc quay $\alpha$

Điểm O gọi là tâm quay, $\alpha$ gọi là góc quay.

Phép quay tâm O góc $\alpha$ kí hiệu là  ${\mathrm{Q}}_{\left(\mathrm{o};\mathrm{\alpha }\right)}$

Câu hỏi:

- Phép quay nào biến lá cờ (C) thành lá cờ (C') .................................................................

- Phép quay nào biến lá cờ (C') thành lá cờ (C).................................................................

2. Tính chất

Phép tịnh tiến là phép biến hình biến:

- Bảo toàn khoảng cách giữa hai điểm bất kì.

- Biến một đường thẳng thành một đường thẳng.

- Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho.

- Biến một tam giác thành một tam giác bằng tam giác đã cho.

- Biến một đường tròn thành đường tròn có cùng bán kính.

Lưu ý. Giả sử phép quay tâm O góc quay $\alpha$ biến đường thẳng d thành đường thẳng d'

 Khi đó:

- Nếu $0\le \mathrm{\alpha }\le \frac{\mathrm{\pi }}{2}$ thì góc giữa d và d' bằng  $\alpha$

- Nếu $\frac{\mathrm{\pi }}{2}\le \mathrm{\alpha }\le \mathrm{\pi }$ thì góc giữa d và d' bằng $\mathrm{\pi }-\mathrm{\alpha }$

3. Phương pháp xác định ảnh một điểm qua phép quay

Phương pháp 1. Sử dụng định nghĩa

Trong mặt phẳng tọa độ Oxy, gọi $\mathrm{M}{}_{\text{'}}({\mathrm{x}}_{{\mathrm{M}}^{\text{'}}};{\mathrm{y}}_{{\mathrm{M}}^{\text{'}}})$ là ảnh của $\mathrm{M}({\mathrm{x}}_{\mathrm{M}};{\mathrm{y}}_{\mathrm{M}})$ qua phép quay tâm $\mathrm{I}(\mathrm{a};\mathrm{b})$ góc quay $\alpha$ Khi đó:  $\mathrm{M}{}_{\text{'}}({\mathrm{x}}_{{\mathrm{M}}^{\text{'}}};{\mathrm{y}}_{{\mathrm{M}}^{\text{'}}})={\mathrm{Q}}_{(\mathrm{O};\mathrm{\alpha })}\left(\mathrm{M}\right)\iff \left\{\begin{array}{l}\mathrm{I}{\mathrm{M}}^{\text{'}}=\mathrm{I}\mathrm{M}\left(1\right)\\ \widehat{\mathrm{M}\mathrm{I}{\mathrm{M}}^{\text{'}}}=\mathrm{\alpha }\left(2\right)\end{array}\right.\begin{array}{c}\end{array}$

Từ (1), sử dụng công thức tính độ dài, sẽ tìm được phương trình thứ nhất theo 2 ẩn.

Từ (2), sử dụng định lý hàm số cos, sẽ tìm được phương trình thứ hai theo 2 ẩn.

Giải hệ phươngtrình này tìm được ${\mathrm{x}}_{\mathrm{M}},{\mathrm{y}}_{\mathrm{M}}$ từ đó suy ra tọa độ điểm  $\mathrm{M}{}_{\text{'}}({\mathrm{x}}_{{\mathrm{M}}^{\text{'}}};{\mathrm{y}}_{{\mathrm{M}}^{\text{'}}})$

Phương pháp 2. Sử dụng công thức tọa độ.

$\mathrm{M}{}_{\text{'}}({\mathrm{x}}_{{\mathrm{M}}^{\text{'}}};{\mathrm{y}}_{{\mathrm{M}}^{\text{'}}})={\mathrm{Q}}_{(\mathrm{I};\mathrm{\alpha })}\left(\mathrm{M}\right)\iff \left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{M}}^{\text{'}}}=({\mathrm{x}}_{\mathrm{M}}-\mathrm{a})\cos \mathrm{\alpha }-({\mathrm{y}}_{\mathrm{M}}-\mathrm{b})\sin \mathrm{\alpha }+\mathrm{a}\\ {\mathrm{y}}_{{\mathrm{M}}^{\text{'}}}=({\mathrm{x}}_{\mathrm{M}}-\mathrm{a})\sin \mathrm{\alpha }-({\mathrm{y}}_{\mathrm{M}}-\mathrm{b})\cos \mathrm{\alpha }+\mathrm{b}\end{array}\right.\begin{array}{c}\end{array}$

3. Hai hình bằng nhau. Hai hình được gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia