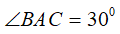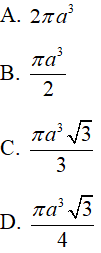Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đề kiểm tra Học kì 1 Toán lớp 12 năm 2023 - 2024 có đáp án, tài liệu bao gồm 20 trang, tuyển chọn 50 câu trong 1 đề thi Toán lớp 12 Học kì 1 với đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi Học kì 1 môn Toán lớp 12 sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 12 bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Bộ 30 đề thi Học kì 1 Toán 12 năm 2023 - 2024 có đáp án - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2023 - 2024

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1 : Hàm số y = x³ - 3x² - 9x nghịch biến trên các khoảng nào sau đây?

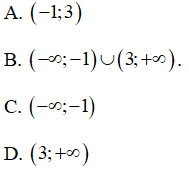
Câu 2 : Hàm số 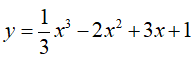 đồng biến trên các khoảng nào sau đây?

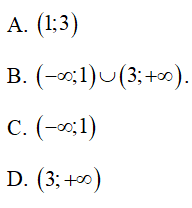
Câu 3 : Rút gọn biểu thức: 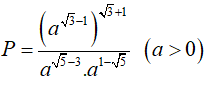 . Kết quả là:

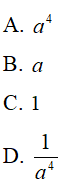
Câu 4 : Điểm cực đại của hàm số y = x(3 - x)² là những điểm nào sau đây?

A. (1;3)

B. (3;0)

C. (1;4)

D. Đáp án khác

Câu 5 : Giá trị lớn nhất của hàm số y = x³ - 3x² - 9x + 35 trên đoạn [-4 ; 4] bằng. Chọn 1 câu đúng.

A. 8

B. 15

C. -41

D. 40

Câu 6 : Tập xác định của hàm số y = (2x² - x - 6)^-5 là:

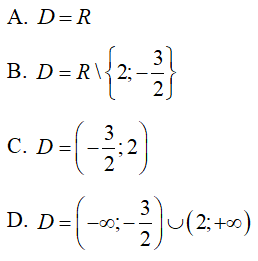
Câu 7 : Tính thể tích V của hình hộp chử nhật ABCD.A'B'C'D' , biết AB = 3cm, AD = 6cm , CC' = 9cm là:

A. V = 18cm

B. V = 18cm³

C. v = 81cm³

D. V = 162cm³

Câu 8 : Để tìm các điểm cực trị của hàm số f(x) = 4x⁵ - 5x⁴ một học sinh lập luận qua ba bước sau:

Bước 1: Hàm số có tập xác định D = R

Ta có: f'(x) = 20x³(x - 1)

f'(x) = 0 ⇔ x³(x - 1) = 0 ⇔ x = 0 hoặc x = 1

Bước 2: Đạo hàm cấp hai f''(x) = 20x²(4x - 3)

Suy ra: f''(0) 0 , f''(1) = 20 > 0

Bước 3: Từ các kết quả trên kết luận:

Hàm số không đạt cực trị tại x = 0

Hàm số đạt cực tiểu tại x = 1

Vậy hàm số chỉ có một cực tiểu duy nhất, đạt tại điểm x = 1

A. Lập luận hoàn toàn đúng

B. Sai từ bước 1

C. Sai từ bước 2

D. Sai từ bước 3

Câu 9 : Cho hàm số y = x³ - 3x² - 9x + 4 . Nếu hàm số đạt cực đại và cực tiểu thì tích số y_CD, y_CT bằng:

A. 25

B. Hàm số không đạt cực đại và cực tiểu.

C. -207

D. -82

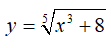
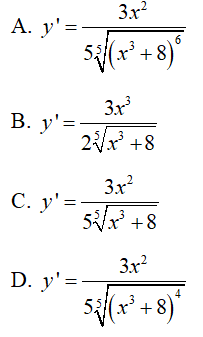
Câu 10 : Đạo hàm của hàm số  là:

Câu 11 : Tìm giá trị lớn nhất của hàm số 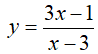 trên đoạn [0;2]

Câu 12 : Giá trị nhỏ nhất của hàm số 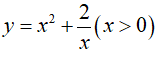 là:

A. 1

B. 2

C. 3

D. 4

Câu 13 : Hàm số nào sau đây nghịch biến trên khoảng (0; +∞) ?

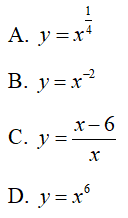
Câu 14 : Cho hàm số 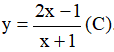 Các phát biểu sau, phát biểu nào Sai ?

A. Hàm số luôn đồng biến trên từng khoảng của tập xác định của nó;

B. Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 2 .

C. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1 ;

D. Đồ thị hàm số (C) có giao điểm với Oy tại điểm có hoành độ là  ;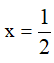

Câu 15 : Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào sao đây? Chọn 1 câu đúng.

Câu 16 : Biết log2 = 2, log3 = b . Tính log45 theo a và b .

A. 2b + a + 1

B. 2b - a + 1

C. 15b

D. a - 2b + 1

Câu 17 : Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.

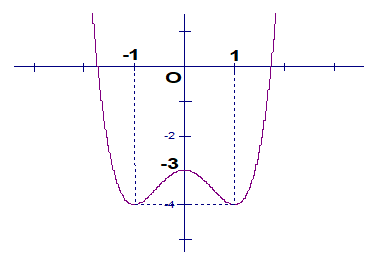
A. 

B. y = x⁴ - 2x² - 3

C. y = x⁴ + 2x² - 3

D. y = x⁴ - 3x² - 3

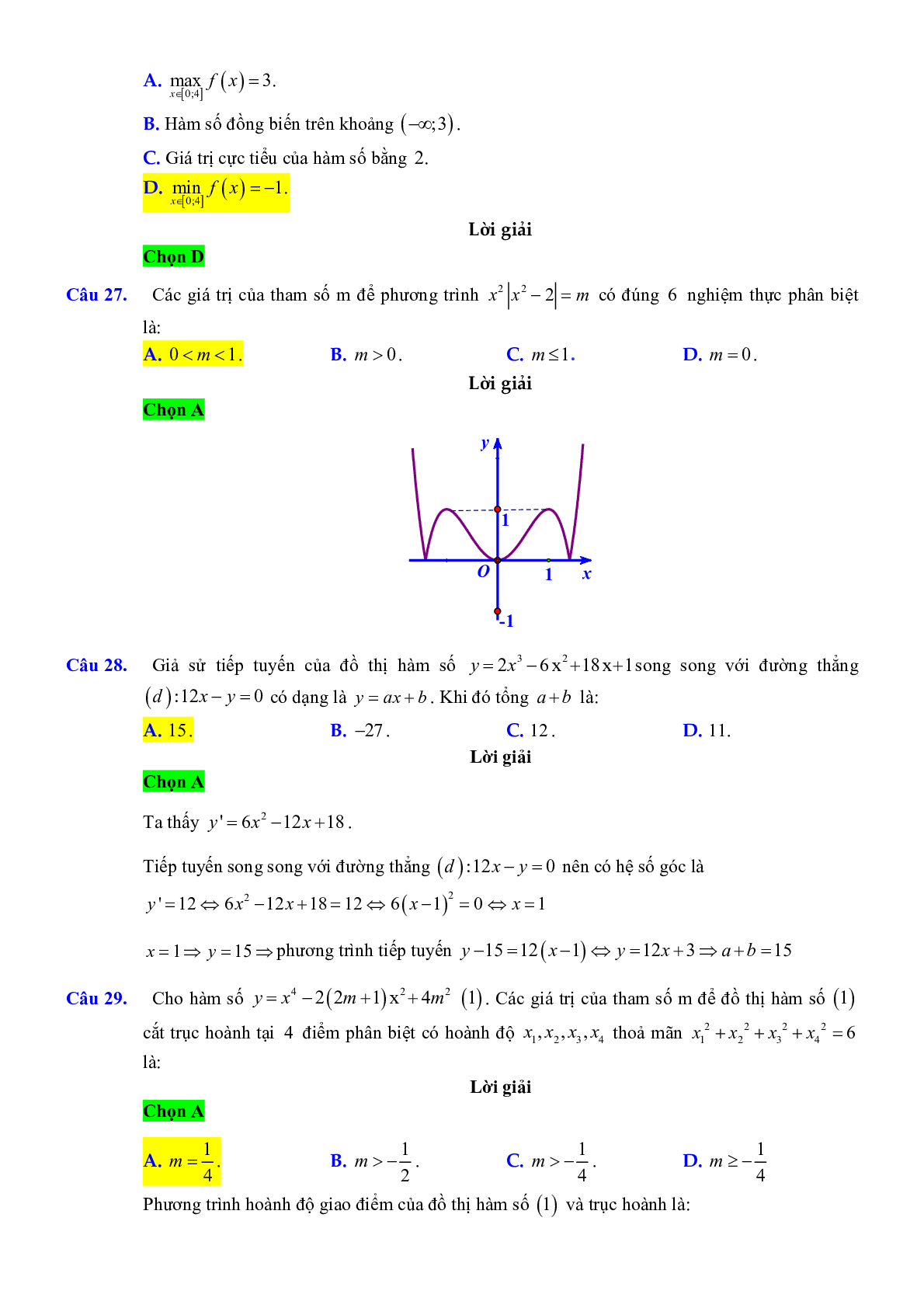
Câu 18 : Tìm m để phương trình x³ + 3x² - 2 = m + 1 có 3 nghiệm phân biệt.

A. -2 < m < 0

B. 2 < m < 4

C. -3 < m < 1

D. 0 < m < 3

Câu 19 : Hàm số y = log₅^{(4x - x)2} có tập xác định là :

A. (2;6)

B. (0;4)

C. (0;+∞)

D. R

Câu 20 : Có bao nhiêu loại khối đa diện đều?

A. 3

B. Vô số

C. 5

D. 20

Câu 21 : Cho hàm số 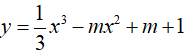 . Tìm m để hàm số đạt cực đại và cực tiểu. thỏa mãn x²_A + x²_B = 2 :

A. m = ±1

B. m ≠ 0

C. m = 2

D. m = ± 3

Câu 22 : Đường thẳng Δ: y = -x + m cắt đồ thị hàm số 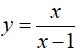 tại hai điểm phân biệt, ứng với các giá trị của là:

D. Kết quả khác

Câu 23 : Cho f(x)= ln²x . Đạo hàm f'(e) bằng :

Câu 24 : Cho đường cong 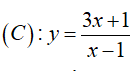 . Tích số các khoảng cách từ một điểm bất kỳ trên (C) đến hai đường tiệm cận của (C) bằng:

A. 2

B. 3

C. 4

D. Kết quả khác

Câu 25 : Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6a, AC = 7a và AD = 4a. Tính thể tích V của tứ diện ABCD.

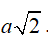
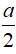
Câu 26 : Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B. AB =  . SA vuông góc với đáy và SA =  . Tính khoảng cách từ điểm A đến mp(SBC)

Câu 27 : Các tiếp tuyến của đường cong (C): y = x³ - 4 đi qua điểm A(2;4) có phương trình là:

A. y = 2x + 1 ; y = 12

B. y = 4x - 1 ; y = 9x + 3

C. y = x - 1 ; y = 3x + 2

D. y = 3x - 2 ; y = 12x + 20

Câu 28 : Cho hàm số 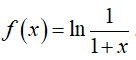 . Hệ thức giữa y và y' không phụ thuộc vào x là :

A. y' - 2y = 1

B. y' - e^y = 0

C. y.y' - 2 = 0

D. y' - 4e^y = 0

Câu 29 : Một tên lửa bay vào không trung với quãng đường đi được với quãng đường s(t) (km) là hàm phụ thuộc theo biến t (giây) theo quy tắc sau : s(t) = e^{t2 + 3} + 2t.e^{3t + 1} (km) . Hỏi vận tốc của tên lửa sau 1 giây là bao nhiêu (biết hàm biểu thị vận tốc là đạo hàm biểu thị quãng đường thời gian).

A. 5e⁴(km)

B. 3e⁴(km)

C. 9e⁴(km)

D. 10e⁴(km)

Câu 30 : Đường thẳng y = x + m là tiếp tuyến của đồ thị hàm số y = x³ + x + 1 , ứng với giá trị m là:

A. m = 2, m = 3

B. m = -4, m = 4

C. m = 1, m = 5

D. m = 0, m = 1

Câu 31 : Tiếp tuyến của đồ thị hàm số y = x³ - 3x² + 1 vuông góc với đường thẳng x - 3y = 0 có phương trình là:

A. 3

B. 2

C. 1

D. 0

Câu 32 : Với giá trị nào của m thì đồ thị hàm số y = x³ + (m - 1)x² - mx + 1 đạt cực trị tại điểm

A. m = 0

B. m = 2

C. m = 1

D. m = -1

Câu 33 : Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.

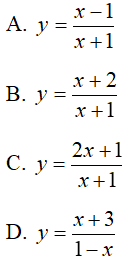
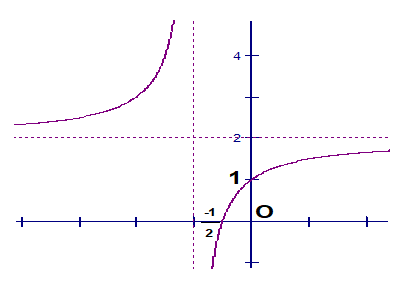
Câu 34 : Cho hàm số 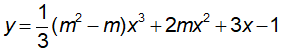 . Tìm m để hàm số luôn đồng biến trên R

A. -3 ≤ m ≤ 0

B. -3 < m ≤ 0

C. -3 ≤ m < 0

D. -3 < m < 0

Câu 35 : Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều. Tỉ số thể tích của khối chóp A'.ABC và khối lăng trụ ABC.A'B'C' là :

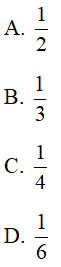
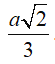
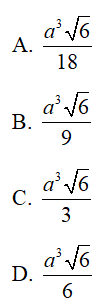
Câu 36 : Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và chiều cao của hình chóp là  . Tính theo a thể tích khối chóp S.ABC

Câu 37 : Cho hàm số y = x³ - 3x² - mx + 2 . Tìm m để hàm số đồng biến trên khoảng (0;+∞) .

A. m = -3

B. m ≤ -3

C. m > -3

D. m < -3

Câu 38 : Cho hàm số y = mx⁴ + (m² - 9)x² + m . Tìm m để hàm số có 3 điểm cực trị

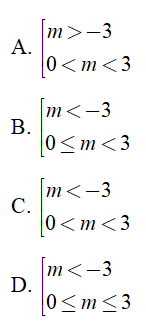
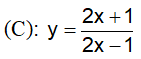
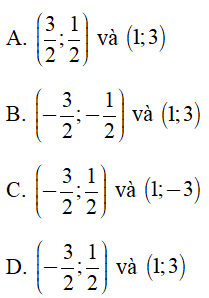
Câu 39 : Tìm tọa độ giao điểm của đường cong  và đường thẳng y = x + 2 .

Câu 40 : Cho hàm số 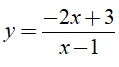 có đồ thị là (C) . Viết phương trình tiếp tuyến của (C) tại các giao điểm của (C) và đường thẳng y = x - 3 .

A. y = -x -3, y = -x + 1

B. y = x + 3, y = -x + 1

C. y = -x -3, y = x + 1

D. y = x + 3, y = -x + 1

Câu 41 : Hàm số 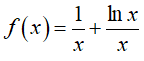 có đạo hàm là :

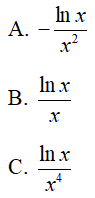
D. Kết quả khác

Câu 42 : Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng:

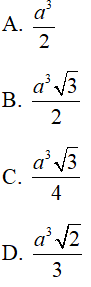
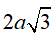
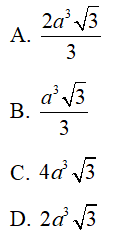
Câu 43 : Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B. AB = 2a, BC = a. AA' =  . Tính theo a thể tích khối lăng trụ ABC.A'B'C' .

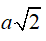
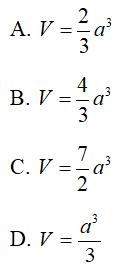
Câu 44 : Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng 2a . Tam giác SAB cân tại S và mặt bên (SAB) vuông góc với mặt phẳng đáy. Biết SA bằng  . Tính thể tích khối chóp S.ABCD.

Câu 45 : Cho tứ diện đều ABCD cạnh bằng a. Tính cosin góc giữa mặt bên và mặt đáy bằng:

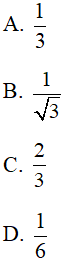
Câu 46 : Một hình hộp chử nhật ABCD.A'B'C'D' nội tiếp mặt cầu, biết AB = a, AD = b , AA' = c khi đó bán kính r của mặt cầu bằng:

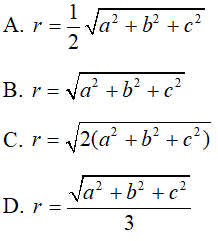
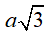
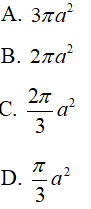
Câu 47 : Cho hình chóp tứ giác S.ABCD có đáy là hình bình hành .SA vuông góc với mặt phẳng đáy. Biết SA bằng  . Tính diện tích mặt cầu tâm I tiếp xúc mp(ABCD)(I là trung điểm của SC)

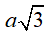
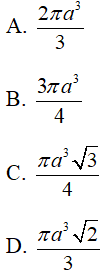
Câu 48 : Cho hình chử nhật ABCD có tâm O và AB = a, AD =  .Trên đường thẳng vuông góc mặt phẳng (ABCD) tại A, lấy điểm S sao cho SC hợp với (ABCD) một góc 45^o. Gọi (S) là mặt cầu tâm O và tiếp xúc với SC. Thể tích khối cầu S bằng:

Câu 49 : Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh a. Thể tích của khối trụ bằng:

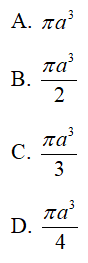
Câu 50 : Trong không gian cho tam giác vuông ABC vuông tại B góc  .Cạnh BC=a, khi quay tam giác ABC quanh cạnh AB thì đường gấp khúc ABC tạo thành hình nón tròn xoay. Thể tích của khối nón này bằng: