Tài liệu Bộ đề thi Toán lớp 12 học kì 1 năm học 2022-2023 gồm 15 đề thi tổng hợp từ đề thi môn Toán 12 của các trường THPT trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 1 Toán lớp 12. Mời các bạn cùng đón xem:

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 1)

Câu 1. Cho hàm số \(y = \frac{{x - 4}}{{x - 2}}\). Khẳng định nào sau đây là đúng:

A. Hàm số nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)

B. Hàm số đồng biến trên trên khoảng \(\left( { - \infty ;4} \right)\)

C. Hàm số đồng biến trên trên khoảng \(\left( {2;4} \right)\)

D. Hàm số nghịch biến trên trên khoảng \(\left( {4; + \infty } \right)\)

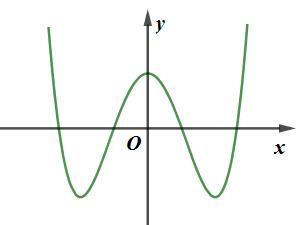
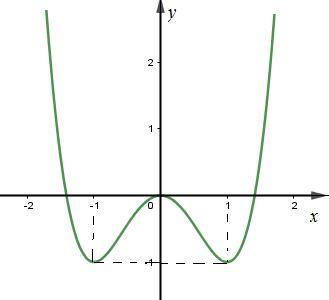
Câu 2. Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ kề bên. Khẳng định nào sau đây là sai?

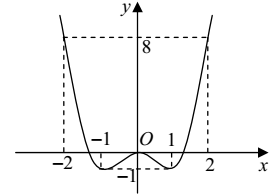
A. Hàm số đạt cực tiểu tại \[x =  \pm 1\], \({y_{CT}} =  - 1\)

B. Hàm số đạt cực đại tại \(x = 0\), $y_{CĐ}=0$

C. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\)

D. Hàm số nghịch biến trên khoảng \(\left( { - 2; - 1} \right)\)

Câu 3. Cho hàm số\(y = \frac{{x - 1}}{{x + {m^2}}}\). Giá trị nhỏ nhất của hàm số trên đoạn\(\left[ {0;3} \right]\) bằng \( - \frac{1}{4}\) khi:

A . \(m = 0\)                B. \(m =  - 2\)

C. \(m = 2\)                  D. \(m =  \pm 2\)

Câu 4. Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = x\left( {2 - \ln x} \right)\) trên đoạn \(\left[ {2;3} \right]\) bằng:

A. \(10 - 2\ln 2 - 3\ln 3\)                    

B. \(4 - 2\ln 2 + e\)     

C. \(6 - 3\ln 3 + e\)     

D. \(10 - 2\ln 2 - 3\ln 3 + e\)

Câu 5. Giá trị lớn nhất của hàm số \(f\left( x \right) = {e^{3x + 2}}\left( {4{x^2} - 5x} \right)\) trên đoạn \(\left[ {\frac{1}{2};\frac{3}{2}} \right]\) bằng:

A. \(\frac{3}{2}{e^{\frac{{13}}{2}}}\)                  

B. \(\frac{4}{5}{e^{\frac{{12}}{5}}}\)                  

C. \(\frac{5}{2}{e^{\frac{{11}}{4}}}\)                                  

D. \(\frac{2}{3}{e^{\frac{{14}}{3}}}\)

Câu 6. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn \(\left[ { - 1;2} \right]\). Tỉ số \(\frac{M}{m}\) bằng:

A. \( - 2\)   

B. \( - \frac{1}{2}\)

C. \( - \frac{1}{3}\)

D. \( - 3\)

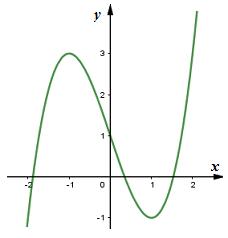
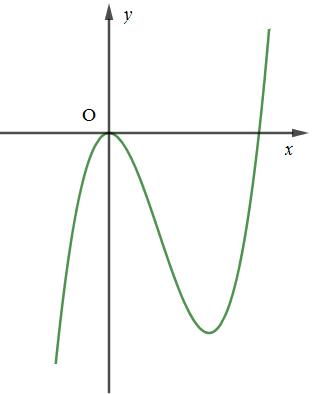
Câu 7.  Đường cong hình bên là đồ thị của hàm số nào sau đây:

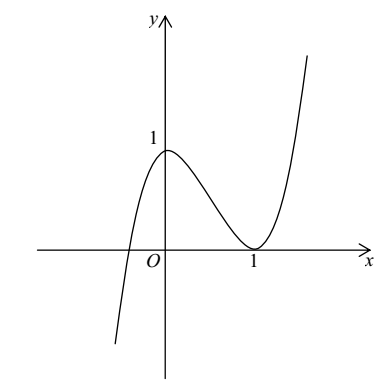
A. \(y = {x^3} - 3{x^2} + 1\)

B. \(y = 2{x^3} + 3x + 1\)       

C. \(y = 2{x^3} - 3{x^2} + 1\)                   

D. \(y = {x^3} - 3x + 1\)

Câu 8. Cho hàm số \(\left( C \right):y = {x^3} - 3{x^2} + 1\). Tiếp tuyến của (C) song song với đường thẳng \[\left( d \right):y =  - 3x + 6\] có phương trình là:

A. \[{\mathop{\rm y}\nolimits}  =  - 3x - 2\]

B. \[{\mathop{\rm y}\nolimits}  =  - 3x + 2\]           

C. \[{\mathop{\rm y}\nolimits}  =  - 3x + 5\]    

D. \[{\mathop{\rm y}\nolimits}  =  - 3x + 1\]

Câu 9. Trong các đồ thị dưới đây, đồ thị nào là đồ thị của hàm số \(y = \frac{{x + 1}}{{1 - x}}\)?

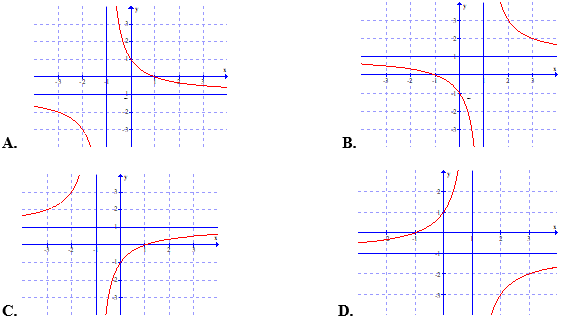
Câu 10: Tiếp tuyến của đồ thị hàm số \[y\, = \,\frac{4}{{x\, - \,1}}\,\]tại điểm có hoành độ \({x_o} =  - 1\)có phương trình là:

A. \(y =  - x - 2\)       

B. \(y =  - x + 3\)

C. \(y =  - x + 2\) 

D. \(y =  - x - 3\)

Câu 11. Cho hàm số \(y = \frac{{2x + 3}}{{x - 2}}\) có đồ thị (C). Tìm m để đường thẳng \(\left( d \right):y = 2x + m\) cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho tiếp tuyến của (C) tại A, B song song nhau ?

A. \(m =  - 2\)              B. \(m =  - 1\)

C. \(m = 0\)                 D. \(m = 1\)

Câu 12. Giá trị của m để tiếp tuyến của đồ thị hàm số\(y = {x^3} + 3m{x^2} + \left( {m + 1} \right)x + 1\)tại điểm có hoành độ \(x =  - 1\) đi qua điểm \(A\left( {1;2} \right)\) là:

A. \(m = \frac{3}{4}\)     

B. \(m = \frac{4}{5}\)         

C. \(m =  - \frac{2}{3}\)           

D. \(m = \frac{5}{8}\)

Câu 13. Cho hàm số \(y = {x^3} - 3{x^2} - mx + 2\). Tập hợp tất cả các giá trị của m để hàm số đã cho đồng biến trên khoảng \(\left( {0; + \infty } \right)\) là:

A. \(m \le  - 3\)          B. \(m \le  - 2\) 

C. \(m \le  - 1\)          D. \(m \le 0\)           

Câu 14. Tìm số m lớn nhất để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {4m - 3} \right)x + 2017\)đồng biến trên R ?

A. \(m = 1\)                B. \(m = 2\)   

C. \(m = 3\)                 D. \(m = 4\)

Câu 15. Số đường tiệm cận của đồ thị hàm số \(y = \frac{{x + 3}}{{\sqrt {{x^2} + 1} }}\) là :

A. 0                             B. 1 

C. 2                              D. 3

Câu 16. Cho hàm số \(\left( C \right):y = \frac{{4x - 3}}{{x - 3}}\). Tổng các khoảng cách bé nhất từ điểm M thuộc (C) đến hai đường tiệm cận của đồ thị (C) là:

A. 3                             B. 4  

C. 6                             D. 9

Câu 17. Cho hàm số \(y = 2{x^3} - 6x\). Khẳng định nào sau đây là sai?

A. Hàm số đạt cực đại tại \(x =  - 1\)

B. Hàm số đạt cực tiểu tại \(x = 1\)

C. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\)

D. Hàm số nghịch biến trên khoảng \(\left( { - 2;1} \right)\)

Câu 18. Cho hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - m - 1} \right)x\). Giá trị m để hàm số đạt cực đại tại \(x = 1\) là:

A. \(m = 0\)                 B. \(m = 2\) 

C. \(m = 3\)                  D. \(m = 5\)

Câu 19. Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}{\left( {x + 1} \right)^3}{\left( {x - 2} \right)^4}\). Số điểm cực trị của hàm số là:

A. 0                             B. 1 

C. 2                              D. 3

Câu 20. Cho hàm số \(y = {x^3} - 3\left( {m + 1} \right){x^2} + 9x - m\). Giá trị nào của m sau đây thì hàm số đã cho có hai điểm cực trị \({x_1}\),\({x_2}\) thỏa mãn \(\left| {{x_1} - {x_2}} \right| = 2\):

A. \(m =  - 3\)              B. \[m = 1\]

C. \(m = 5\)                  D. cả A và B.

Câu 21. Cho hàm số \(y = {x^4} - 2m{x^2} + 2m + {m^4}\). Tìm m để hàm số đã cho có ba điểm cực trị  và các điểm cực trị tạo thành một tam giác có diện tích bằng 1 ?

A. \(m = 0\)                 B. \(m =  - 2\)

C. \(m =  - 1\)               D. \(m = 1\)

Câu 22. Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị của m để phương trình \[f\left( x \right) = m + 1\] có ba nghiệm phân biệt là:

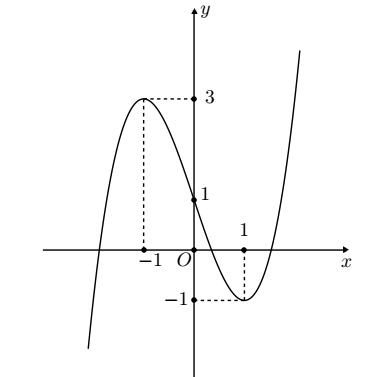
A. \( - 1 < m < 3\)                   

B. \( - 2 < m < 4\)                   

C. \( - 2 < m < 2\)                   

D. \( - 1 < m < 2\)

Câu 23. Điều kiện của tham số m để đường thẳng \(\left( d \right):y = x + 5\)cắt đồ thị hàm số \(y = {x^3} - 2\left( {m - 1} \right){x^2} + \left( {2m - 3} \right)x + 5\) tại ba điểm phân biệt là:

A. \(m \ne 2\)              

B. \(1 < m < 5\)                      

C. \(m < 1 \vee m > 5\)                      

D. \(\forall m \in R\)

Câu 24. Số giao điểm của đồ thị hàm số\(y = {x^4} + {x^2} + 3x - 2\)và đường thẳng \(\left( d \right):y = 3x - 2\)là:

A. 0                             B. 1

C. 2                              D. 3

Câu 25. Cho hàm số \(\left( C \right):y = \frac{{2x + 1}}{{x - 1}}\) và điểm \(M\left( {2;5} \right)\)thuộc (C). Tiếp tuyến của (C) tại điểm M cắt trục tọa độ \(Ox\), \(Oy\) lần lượt tại điểm A và B. Diện tích của tam giác OAB bằng :

A. \(\frac{{121}}{6}\)                                  

B. \(\frac{{112}}{5}\)                       

C. \(\frac{{122}}{3}\)                                   

D. \(\frac{{97}}{2}\)

Câu 26. Được sự hỗ trợ từ Ngân hàng Chính sách xã hội địa phương, nhằm giúp đỡ các sinh viên có hoàn cảnh khó khăn hoàn thành việc đóng học phí học tập, một bạn sinh viên A đã vay của ngân hàng 20 triệu đồng với lãi suất 12%/năm, và ngân hàng chỉ bắt đầu tính lãi sau khi bạn A kết thúc khóa học. Bạn A đã hoàn thành khóa học và đi làm với mức lương là 5,5 triệu đồng/tháng. Bạn A dự tính sẽ trả hết nợ gốc lẫn lãi suất cho ngân hàng trong 36 tháng. Hỏi số tiền m mỗi tháng mà bạn A phải trả cho ngân hàng là bao nhiêu?

A. \(m = \frac{{{{1,12}^3} \times 20 \times 0,12}}{{\left( {{{1,12}^3} - 1} \right) \times 12}}\)      triệu 

B. \(m = \frac{{{{1,12}^2} \times 20 \times 0,12}}{{\left( {{{1,12}^2} - 1} \right) \times 12}}\)        triệu 

C. \(m = \frac{{{{1,12}^3} \times 36 \times 0,12}}{{\left( {{{1,12}^3} - 1} \right) \times 12}}\)    triệu

D. \(m = \frac{{{{1,12}^2} \times 36 \times 0,12}}{{\left( {{{1,12}^2} - 1} \right) \times 12}}\)        triệu

Câu 27. Tập xác định của hàm số\(y = {\left( {2{x^2} - 3x + 1} \right)^{\frac{3}{2}}}\) là:

A. \(\left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right)\)  

B. \(\left( { - \infty ; - 1} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\)   

C. \(\left( {\frac{1}{2};1} \right)\)                

D. \(\left( { - 1;\frac{1}{2}} \right)\)

Câu 28. Đạo hàm của hàm số \(y = \log \left( {4x} \right)\) là:

A. \(y' = \frac{4}{{x\ln 10}}\)                      

B. \(y' = \frac{1}{{x\ln 10}}\)                                   

C. \(y' = \frac{1}{{4x\ln 10}}\)           

D. \(y' = \frac{{\ln 10}}{{4x}}\)

Câu 29. Biết \(\log 2 = a\),\(\log 3 = b\) thì \(\log 45\) tính theo a và b bằng:

A. \(2b - a + 1\)  

B. \(2b + a + 1\)   

C. \(15b\)  

D. \(a - 2b + 1\)

Câu 30. Cho \({\log _2}x = \frac{1}{5}\). Giá trị biểu thức \(P = \frac{{{{\log }_2}\left( {8x} \right) - {{\log }_2}\frac{x}{4}}}{{1 + {{\log }_4}x}}\) bằng:

A. \(\frac{5}{7}\)                                          

B. \(\frac{5}{6}\)                   

C. \(\frac{{50}}{{11}}\)                                          

D. \(\frac{{10}}{{11}}\)

Câu 31. Tổng các nghiệm của phương \({4^{x + 1}} - {6.2^{x + 1}} + 8 = 0\)là:

A. 1                             B. 3

C. 5                             D. 6

Câu 32. Số nghiệm của phương trình \(\log \left( {x - 3} \right) - \log \left( {x + 9} \right) = \log \left( {x - 2} \right)\) là:

A. 0                             B. 1 

 C. 2                              D. Nhiều hơn 2

Câu 33. Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^{3x}} < {\left( {\frac{1}{9}} \right)^{x - 1}}\) là :

A. \(\left( { - 2; + \infty } \right)\)                  

B. \(\left( { - \infty ; - 2} \right)\)                               

C. \(\left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right)\)           

D. \(\emptyset \)

Câu 34. Tập nghiệm của bất phương trình \({\log _{0,8}}\left( {{x^2} + x} \right) < {\log _{0,8}}\left( { - 2x + 4} \right)\) là :

A. \(\left( { - \infty ; - 4} \right) \cup \left( {1; + \infty } \right)\)     

B. \(\left( { - 4;1} \right)\)                  

C. \(\left( { - \infty ; - 4} \right) \cup \left( {1;2} \right)\)                      

D. \(\left( { - 4;1} \right) \cup \left( {2; + \infty } \right)\)

Câu 35. Cho phương trình \({4^x} - m{.2^{x + 2}} + 2m = 0\). Nếu phương trình này có hai nghiệm \({x_1},{x_2}\) thõa mãn \({x_1} + {x_2} = 4\)thì m có giá trị bằng:

A. 1                             B. 2

C. 4                              D. 8

Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi E, F lần lượt là trung điểm của SB, SD. Tỉ số \(\frac{{{V_{S.AEF}}}}{{{V_{S.ABCD}}}}\)bằng:

A. \(\frac{1}{2}\)        B. \(\frac{1}{8}\)

C. \(\frac{1}{4}\)        D. \(\frac{3}{8}\)

Câu 37. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy. Cạnh bên SC hợp với đáy một góc \({30^0}\). Thể tích của khối chóp S.ABC là:

A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)             

B. \(\frac{{{a^3}}}{{12}}\)                         

C. \(\frac{{{a^3}}}{4}\)                                    

D. \(\frac{{{a^3}\sqrt 3 }}{4}\)

Câu 38. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, \(AB = a\sqrt 2 \), SA vuông góc với đáy. Góc giữa (SBC) và mặt đáy bằng \({60^0}\). Thể tích của khối chóp S.ABC là:

A. \(\frac{{{a^3}\sqrt 3 }}{2}\)                    

B. \(\frac{{{a^3}\sqrt 3 }}{6}\)                    

C. \(\frac{{{a^3}\sqrt 6 }}{3}\)                         

D. \(\frac{{{a^3}\sqrt 3 }}{3}\)

Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng \({30^0}\). Thể tích của khối cầu ngoại tiếp hình chóp S.ABCD là:

A. \(\frac{{8\sqrt 6 }}{9}\pi {a^3}\)             

B. \(\frac{{64\sqrt 6 }}{{27}}\pi {a^3}\)                 

C. \(\frac{{8\sqrt 6 }}{{27}}\pi {a^3}\)                        

D. \(\frac{{32}}{9}\pi {a^3}\)

Câu 40. Cho hình chóp tứ giác đều S.ABCD có các cạnh cùng bằng a. Bán kính mặt cầu ngoại tiếp hình chóp là:

A.\(a\sqrt 2 \)        B. \(\frac{{a\sqrt 2 }}{2}\)

C. \(a\sqrt 3 \)   D.(\frac{{a\sqrt 3 }}{2}\)

Câu 41. Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, mặt phẳng (A’BC) hợp với đáy một góc \({60^0}\). Thể tích của khối lăng trụ ABC.A’B’C’ là:

A. \(\frac{{3\sqrt 3 {a^3}}}{4}\)                 

B. \(\frac{{3\sqrt 3 {a^3}}}{8}\)                  

C. \(\frac{{3\sqrt 3 {a^3}}}{2}\)                         

D. \(\frac{{{a^3}\sqrt 3 }}{8}\)

Câu 42. Cho hình lăng trụ tam giác đều có các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình lăng trụ là:

A. \(7\pi {a^2}\)     

B. \(\frac{{7\pi {a^2}}}{2}\)            

C. \(\frac{{7\pi {a^2}}}{3}\)                       

D. \(\frac{{7\pi {a^2}}}{6}\)

Câu 43. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ A đến mp(SCD) bằng:

A. \(\frac{{a\sqrt {21} }}{5}\)                      

B. \(\frac{{a\sqrt {21} }}{6}\)                      

C. \(\frac{{a\sqrt {21} }}{7}\)                          

D. \(\frac{{a\sqrt {21} }}{8}\)

Câu 44. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B biết \(AD = 2a\), \(AB = BC = a\). Cạnh bên SA vuông góc với đáy, góc giữa SC và mặt đáy bằng \({45^0}\). Thể tích của khối chóp S.ABCD bằng:

A. \(\frac{{3{a^3}\sqrt 2 }}{2}\)                  

B. \(\frac{{{a^3}\sqrt 2 }}{2}\)                    

C. \(\frac{{{a^3}\sqrt 3 }}{2}\)                         

D. \(\frac{{2{a^3}\sqrt 2 }}{3}\)

Câu 45. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu của A’ lên mặt phẳng (ABC) là trung điểm của BC. Biết góc giữa AA’ và mặt đáy bẳng \({60^0}\). Thể tích của khối lăng trụ là:

A. \(\frac{3}{4}{a^3}\)                     

B. \(\frac{{3\sqrt 3 }}{8}{a^3}\)                  

C. \(\frac{3}{8}{a^3}\)                                   

D. \(\frac{{3\sqrt 3 }}{4}{a^3}\)

Câu 46. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, \(AB = a\). Cạnh bên SA vuông góc với mặt đáy. Góc giữa SB và mặt đáy bằng \({45^0}\). Thể tích của khối cầu ngoại tiếp hình chóp S.ABC là:

A. \(\frac{{\sqrt 3 }}{8}\pi {a^3}\)               

B. \(\frac{{\sqrt 3 }}{4}\pi {a^3}\)               

C. \(\frac{{\sqrt 3 }}{2}\pi {a^3}\)                                

D. \(\frac{{\sqrt 3 }}{{16}}\pi {a^3}\)

Câu 47. Cho hình chữ nhật ABCD biết \(AB = 1\), \(AD = \sqrt 3 \). Khi quay hình chữ nhật ABCD xung quanh trục AB thì cạnh CD tạo nên hình trụ tròn xoay. Thể tích của khối trụ là:

A. \(3\pi \)            B. \(\pi \sqrt 3 \) 

C. \(\pi \)      D. \(\frac{{\sqrt 3 }}{3}\pi \)

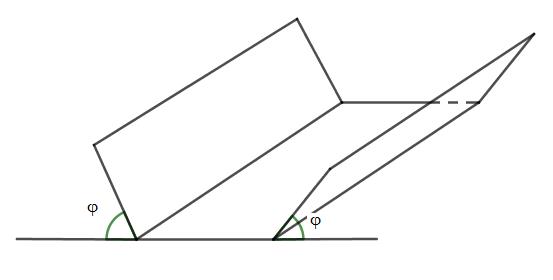
Câu 48. Cho một tấm nhôm hình chữ nhật ABCD biết \(AD = 60cm\). Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ, để được một hình lăng trụ khuyết 2 đáy. Tìm x để thể tích khối lăng trụ lớn nhất:

 

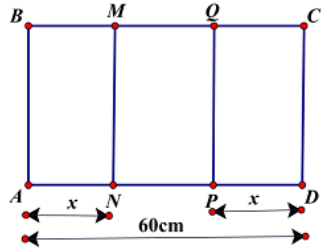
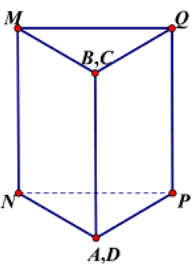
A. \(x = 20\)                    

B. \(x = 30\)                

C. \(x = 45\)                           

D. \(x = 40\)        

 

Câu 49. Cho hình nón tròn xoay có đường cao h = 20cm, bán kính đáy r = 25cm. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Diện tích của thiết diện có giá trị bằng:

A.\({S_{ABC}} = 200c{m^2}\)                              

B. \({S_{ABC}} = 300c{m^2}\)        

C. \({S_{ABC}} = 400c{m^2}\)                      

D. \({S_{ABC}} = 500c{m^2}\)

Câu 50: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng \[a\sqrt 2 \]. Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc 60⁰. Khi đó, diện tích tam giác SBC bằng:

A. \({S_{ABC}} = \frac{{{a^2}\sqrt 2 }}{9}\) 

B. \({S_{ABC}} = \frac{{{a^2}\sqrt 2 }}{3}\)                                                                                              

C. \({S_{ABC}} = \frac{{{a^2}\sqrt 2 }}{4}\)   

D. \({S_{ABC}} = {a^2}\sqrt 2 \)

 

 .................................

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 2

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 2)

Câu 1. Xét hàm số \[y = {x^4} + 2{x^2} - 1\] có đồ thị \(\left( C \right)\).Trong các mệnh đề sau, mệnh đề nào sai

A.    Đồ thị \(\left( C \right)\) đi qua điểm \(A\left( {0; - 1} \right)\) . 

B.     Đồ thị \(\left( C \right)\) có ba điểm cực trị.

C. Đồ thị \(\left( C \right)\) có một điểm cực trị.

D. Đồ thị \(\left( C \right)\) nhận trục tung làm trục đối xứng.

Câu 2. Hình nào trong bốn hình sau là đồ thị hàm số \(y = {x^3} - 3{x^2} + 4x + 1\) ?

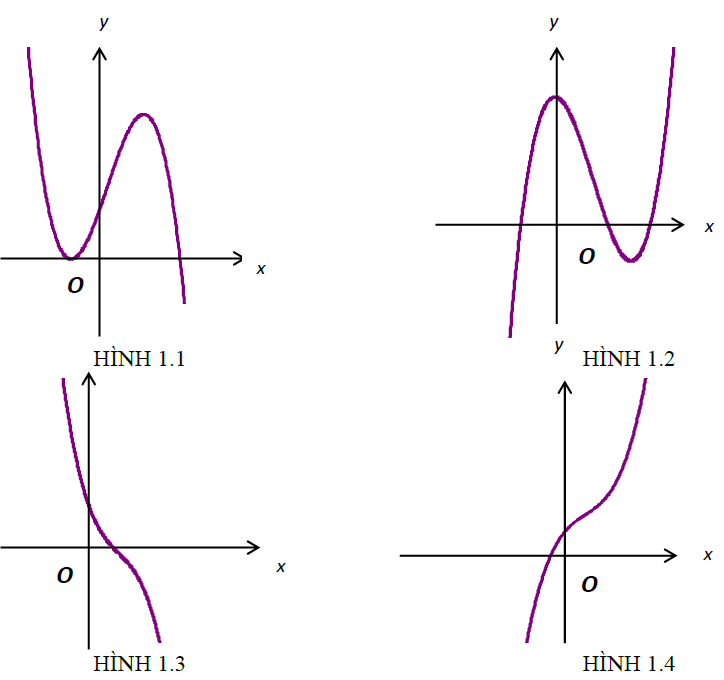
A.    HÌNH 1.1              B. HÌNH 1.2

C.HÌNH 1.3                D.HÌNH 1.4

Câu 3. Bảng biến thiên sau là của hàm số  nào ?

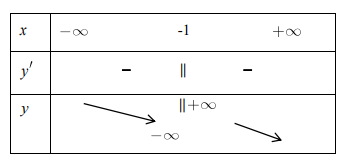
A. \(y = x + \frac{4}{x}\)                  

B. \(y =  - x + \frac{1}{{x + 1}}\)                 

C. \(y = x - \frac{1}{{x + 1}}\)               

D. \[y = \frac{{2x + 1}}{{x + 1}}\]

Câu 4. Hàm số \(y = \frac{1}{x} + x\) đồng biến trên khoảng nào?

A. \(\left( { - 1;0} \right)\).

B. \(\left( { - \infty ;0} \right)\)   

C. \(\left( {2; + \infty } \right)\) 

D. \(\left( {0;1} \right)\)

Câu 5. Chọn mệnh đề đúng

Hàm số \(y =  - 3x + \sin x\)

A. Nghịch biến trên tập xác định.                              

B. Đồng biến trên tập xác định.

C. Nghịch biến trên \(\left( { - \infty ;0} \right)\).                     

D. Đồng biến trên \(\left( {0; + \infty } \right)\).

 Câu 6. Với giá trị nào của m thì hàm số \(y =  - \frac{1}{3}{x^3} + {x^2} + \left( {2m - 3} \right)x + 2017\) nghịch biến trên tập số thực R.

A. \(m > 1\)                  B. \(m < 1\)   

C. \(m \ne 1\)               D. \(m \le 1\)

Câu 7. Giá trị lớn nhất của hàm số  \[y = \frac{{2x - 1}}{x}\] trên \[\left( {2;5} \right]\]là

A.    \(\frac{3}{2}\).              B. \(\frac{5}{3}\). 

C. \(1\).              D. \(\frac{9}{5}\) .

Câu 8. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} + \frac{1}{2}{x^2} - 4x + 3\) trên đoạn \(\left[ { - 2;3} \right]\) lần lượt là a và b. Khi đó tích ab bằng

A. \(\frac{1}{2}\).                                         

B. \(\frac{{185}}{{27}}\).                

C. - 5.                         

D. \(\frac{{45}}{4}\)

Câu 9. Giá trị lớn nhất của hàm số \[y = {\cos ^4}x + {\sin ^2}x + 2\] bằng

A. \(\frac{{11}}{4}\)          B. \(3\) 

C. \(5\)                         D. \(\frac{{13}}{2}\)

Câu 10. Đường tiệm cận ngang của đồ thị hàm số \[y = \frac{{x - 1}}{{3x + 1}}\] có phương trình

A.\(x =  - \frac{1}{3}\)                                  

B. \(x = \frac{1}{3}\)            

C. \(y =  - \frac{1}{3}\)                     

D. \(y = \frac{1}{3}\)

Câu 11. Giá trị m để tiệm cận đứng của đồ thị hàm số \[y = \frac{{2x + 1}}{{x + m}}\] đi qua điểm \[A\left( {2;3} \right)\]là

A.    2.                         B. 0. 

C. 3.                            D. -2.

Câu 12. Giá trị cực đại của hàm số \(y = {x^3} + 3{x^2} - 9x + 5\) là

A. -5.                           B. 0.

C. 32                           D. 1.

Câu 13. Hàm số \(y = f\left( x \right)\) có \({y^/} = {x^2}\left( {x - 1} \right)\left( {3 - 2x} \right)\) . Khi đó số cực trị của hàm số là

A.    0.     

B. 1.       

C. 2.       

D. 3.

Câu 14. Với giá trị nào của m thì hàm số \(y = {x^4} - 2\left( {3m - 4} \right){x^2}\) có ba điểm cực trị

A. \(m > \frac{4}{3}\) 

B. \(m \ge \frac{4}{3}\)

C. \(m < \frac{4}{3}\)  

D. \(m \le \frac{4}{3}\)

Câu 15. Với giá trị nào của m thì hàm số \(y = {x^3} - \frac{1}{2}{x^2} + \left( {1 - 2m} \right)x + 3{m^3} - 4\) có hai cực trị

A.     \(m \le \frac{{11}}{{24}}\) .                              

B. \(m \ge \frac{{11}}{{24}}\) .                   

C. \(m < \frac{{11}}{{24}}\)                    

D. \(m > \frac{{11}}{{24}}\)

Câu 16. Cho hàm số \(y = {x^3} + m{x^2} - 3x + 1 + m\). Giá trị  m để hàm số đạt cực đại tại x = - 3 là

A. m = 1.                        B. \(m = 4\).

C. m = 3.                     D. \(m =  - 4\).

Câu 17. Gọi M, N là giao điểm của đồ thị hàm số \[y = \frac{{2x + 4}}{{x - 1}}\] và đường thẳng \(d:y = x + 1\) . Khi đó hoành độ trung điểm I của đoạn MN là.

A. \( - \frac{5}{2}\)               B.1.

C.2.                             D.  \(\frac{5}{2}\)

Câu 18. Cho hàm số \[y = \frac{{2x + 3}}{{x + 2}}\] có đồ thị là (C).  Giá trị m để đường thẳng \(d:y = x + m\) cắt (C) tại hai điểm phân biệt A, B  sao cho \(AB = \sqrt 5 \) là

A. \(m = 1\,\,\)hoặc \(m = 7\)      

B. \(m = 1\,\,\)            

C. \(m = 7\)                

D. \(m < 2\) hoặc \(m > 6\)

Câu 19. Cho hàm số \(y =  - {x^4} + 2m{x^2} + 1 - 2m\) \(\left( 1 \right)\)

Giá trị m sao cho đồ thị hàm số \(\left( 1 \right)\) cắt trục hoành tại bốn điểm có các hoành độ nhỏ hơn 2 là

A. \(m \ne 1\) và \(\frac{1}{2} < m < \frac{5}{2}\).            

B. \(m \ne 1\)              

C. \(m > \frac{1}{2}\) và \(m \ne 1\)      

D. \(m \ne 1\)

Câu 20. Số giao điểm của đồ thị hàm số \(y = \left( {x - 1} \right)\left( {{x^2} - 2x + 5} \right)\) với trục hoành là

A.    0.       

B. 1.         

C. 2.   

D. 3.

Câu 21. Phương trình \({x^3} - 3x = m\) có ba nghiệm phân biệt khi

A. \(m > 2\) hoặc \(m <  - 2\). 

B. \(m = 2\)  hoặc  \(m =  - 2\)                

C. \(m = 2\)          

D. \( - 2 < m < 2\)

Câu 22. Hệ số góc tiếp tuyến của đồ thị hàm số \[y = \frac{{x - 1}}{{x + 1}}\] tại điểm x = 2 bằng

A.    2.                      B. \(\frac{2}{9}\).

C. \(\frac{2}{3}\).       D. 1.

Câu 23. Hệ số góc tiếp tuyến của đồ thị hàm số \(y =  - {x^2} + 2x - 1\) bằng  - 4. Khi đó hoành độ  tiếp điểm là

A. \(x =  - 3\)     

B. \(x =  - 1\) hoặc \(x = 3\).

C. \(x = 3\)     

D.  x = - 1 .

Câu 24. Phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 1}}\) tại điểm có hoành độ x = 0

A. \(y = x + 1\)            B. \(y =  - x + 1\)

C. \(x = 1\)                   D. y = 2.

Câu 25. Gọi M là điểm thuộc đồ thị (C)  hàm số \(y = \frac{{2x - 1}}{{x + 1}}\)  có tung độ bằng 5. Tiếp tuyến của (C) tại M cắt các trục tọa độ lần lượt tại A, B. Diện tích tam giác OAB là

A. \(\frac{{121}}{6}\)     

B. \(\frac{{119}}{6}\)       

C. \(\frac{{121}}{3}\)             

D. \(\frac{{289}}{{18}}\)

Câu 26. Rút gọn biểu thức A = \({\left( {2a + \frac{b}{2}} \right)^{ - 1}}\)\[\left[ {{{\left( {2a} \right)}^{ - 1}} + {{\left( {\frac{b}{2}} \right)}^{ - 1}}} \right]\];với \(a \ne 0;\,\,b \ne 0\) ta được kết quả

A. \(\frac{1}{{ab}}\)          B. \(ab\) 

C. 1.                     D. \(\frac{2}{{ab}}\)

Câu 27. Cho \({\left( {\sqrt 2  - 1} \right)^m} < {\left( {\sqrt 2  - 1} \right)^n}\). Khi đó

A. \(m > n\).                    B. \(m < n\). 

C. m = n.                     D. \(m \le n\).

Câu 28. Cho hàm số  \(f\left( x \right) = \frac{{{e^x} + {e^{ - x}}}}{{{e^x} - {e^{ - x}}}}\)

A. \({f^/}\left( x \right) = \frac{{ - 4}}{{{{\left( {{e^x} - {e^{ - x}}} \right)}^2}}}\)                                          

B. \({f^/}\left( x \right) = {e^x} + {e^{ - x}}\)

C. \({f^/}\left( x \right) = \frac{{{e^x}}}{{{{\left( {{e^x} - {e^{ - x}}} \right)}^2}}}\)                                      

D. \({f^/}\left( x \right) = \frac{{ - 2}}{{{{\left( {{e^x} - {e^{ - x}}} \right)}^2}}}\)

Câu 29. Tìm mệnh đề sai trong các mệnh đề sau

A. Hàm số \(y = {\log _a}x\) có tập xác định là khoảng \(\left( {0; + \infty } \right)\).

B. Hàm số \(y = {\log _a}x\) với \(a > 1\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\).

C. Hàm số \(y = {\log _a}x\) với \(0 < a < 1\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) .

D. Đồ thị hàm số \(y = {\log _a}x\) có tiệm cận ngang là trục hoành.

Câu 30.  Cho \({5^x} = 3\) . Giá trị \({25^x} + {5^{2 - x}}\)

A. \(\frac{{11}}{3}\)                                    

B. \(\frac{{25}}{3}\)                                     

C. \(\frac{{52}}{3}\)                                         

D. \(\frac{{29}}{3}\).

Câu 31. Phương trình \({\log _3}\left( {3x - 2} \right) = 3\) có nghiệm là

A. \(\frac{{11}}{3}\)         

B. \(\frac{{25}}{3}\)       

C. \(\frac{{29}}{3}\)                                         

D. \(9\)

Câu 32. Một người gởi tiết kiệm A đồng với lãi suất 7,56%  một năm và lãi hàng năm được nhập vào vốn. Hỏi sau bao nhiêu năm người đó sẽ có ít nhất số tiền gấp đôi số tiền ban đầu, giả sử lãi suất không thay đổi.

A. 7.                      B. 8. 

C. 9.                       D. 10.

Câu 33. Phương trình \({3^{2x + 1}} - {4.3^x} + 1 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa

A. \(2{x_1} + {x_2} = 0\)                                                                 

B. \({x_1} + 2{x_2} =  - 1\).

C, \({x_1} + {x_2} =  - 2\)                                                                

D. \({x_1}{x_2} =  - 1\)

Câu 34. Phương trình \({3^{2x}} - \left( {m + 1} \right){3^x} + m = 0\) có đúng hai nghiệm phân biệt khi

A. m = 1.             

B.  m = 0.

C. \(m > 0\).       

D. \(0 < m \ne 1\)

Câu 35. Một học sinh trình bày lời giải  phương trình \[\log _{\sqrt 2 }^2x + 3{\log _2}x + {\log _{\frac{1}{2}}}x = 0\,\,\,\,\left( * \right)\] theo các bước

\[\left( * \right) \Leftrightarrow 2\log _2^2x + 2{\log _2}x = 0\] , \(x > 0\)  (bước 1)

\[ \Leftrightarrow {\log _2}x = 0\] hoặc \[{\log _2}x =  - 1\], \(x > 0\) (bước 2)

\[ \Leftrightarrow x = 1\] hoặc \[x = \frac{1}{2}\](bước 3)

Phương trình có tập nghiệm \[S = \left\{ {\frac{1}{2};1} \right\}\]  (bước 4)

Trình bày lời giải phương trình trên sai trong bước nào dưới đây

A. Bước 1.                 B. Bước 2.

C. Bước 3.                   D. Bước 4.

Câu 36. Thể tích một tứ diện đều bằng  \(\frac{{{a^3}\sqrt 2 }}{{12}}\). Độ dài cạnh của khối tứ diện  đó là

A. a                   B.  \(2a\)   

C.  \(a\sqrt 3 \)             D.  \(a\sqrt 6 \)

Câu 37. Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên hợp với đáy một góc \({45^0}\). Thể tích khối chóp S.ABC bằng

A. \(\frac{{{a^3}}}{4}\)                                           

B. \(\frac{{{a^3}}}{{12}}\)                                     

C. \(\frac{{{a^2}\sqrt 3 }}{4}\)             

D. \(\frac{{a\sqrt 3 }}{3}\)

Câu 38. Cho khối chóp S.ABCD có đáy ABCD là hình vuông, đường chéo  \(AC = a\sqrt 2 \), \(SA \bot \left( {ABCD} \right)\). Cạnh bên SC tạo với đáy một góc \({60^0}\). Thể tích khối chóp S.ABCD bằng

A. \(\frac{{{a^3}\sqrt 6 }}{3}\) 

B. \({a^3}\sqrt 6 \) 

C.\({a^2}\)

D. \(a\sqrt 6 \)

Câu 39. Cho hình chóp S.ABC có đáy ABC đều cạnh a, tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Khoảng cách từ điểm S đến mặt phẳng (ABC) bằng \(\frac{{3a}}{2}\) . Cạnh SA hợp với đáy một góc bằng

A. \({60^0}\)                B. \({30^0}\) 

C. \({45^0}\)                   D. \({90^0}\)

Câu 40. Cho khối chóp đều S.ABCD có cạnh đáy bằng a, có thể tích là  \(\frac{{{a^3}\sqrt 3 }}{8}\). Khoảng cách từ S đến \(\left( {ACD} \right)\) là

A. \(\frac{{3\sqrt 3 a}}{4}\)                         

B.  \(\frac{{3a}}{2}\)                                    

C.  \(\frac{{3\sqrt 3 a}}{8}\)                     

D.  \(\frac{a}{2}\)

Câu 41. Cho khối chóp S.ABC. Gọi A’, B’ theo thứ tự là trung điểm của các đoạn thẳng SA, SB. Trên đoạn thẳng SC lấy  C’ thỏa  3SC’ =  SC. Tỉ số  thể tích \(\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}}\) là

A.    \(\frac{1}{4}\).                                        

B. \(\frac{1}{{12}}\).                        

C. \(\frac{1}{6}\).                             

D. \(\frac{1}{2}\).

Câu 42. Một phòng học có dạng là một hình hộp chữ nhật có chiều dài là 8m, chiều rộng là 6m, thể tích là \(192{m^3}\). Người ta muốn quét vôi trần nhà và bốn bức tường phía trong phòng. Biết diện tích các cửa bằng \(10{m^2}\) . Hãy tính diện tích cần quét vôi.

A.    \(182{m^2}\).                               

B. \(134{m^2}\)..                               

C. \(144{m^2}\).                    

D. \(96{m^2}\).

Câu 43. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại B với BA = BC = a, biết A’B hợp với đáy ABC một góc \({60^0}\). Thể tích khối lăng trụ bằng

A. \(\frac{{{a^3}\sqrt 3 }}{9}\)                                

B. \(\frac{{{a^3}\sqrt 3 }}{2}\)                                

C.\(\frac{1}{2}{a^2}\)                      

D. \(\frac{{{a^3}\sqrt 3 }}{6}\)        

Câu 44. Lăng trụ  đều ABC.A’B’C’ tất cả các cạnh bằng nhau và có thể tích là  \(\frac{{{a^3}\sqrt 3 }}{4}\). Độ dài cạnh của khối lăng trụ là

A. a                     B.  \(2a\)

C.  \(a\sqrt 3 \)             D.  \(a\sqrt 6 \)

Câu 45. Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc nhau và AB = a, AC =2a, AD = 3a. Thể tích tứ diện ABCD bằng

A. \(6{a^3}\)                B.  \(3{a^3}\)

C.  \({a^3}\)                   D.  \(2{a^3}\)

Câu 46. Lăng trụ  ABC.A’B’C’ có đáy ABC là tam giác đều  cạnh a, hình chiếu của A’ lên đáy \(\left( {ABC} \right)\) trùng với trung điểm của BC. Thể tích của khối lăng trụ là  \(\frac{{{a^3}\sqrt 3 }}{8}\). Độ dài cạnh bên khối lăng trụ là

A. a                       B.  \(2a\)

C.  \(a\sqrt 3 \)             D.  \(a\sqrt 6 \)

Câu 47. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, \(AD = a\sqrt 3 \)\(SA \bot \left( {ABCD} \right)\). Cạnh bên SB tạo với mặt phẳng \(\left( {SAD} \right)\) một góc \({60^0}\). Thể tích khối chóp S.ABCD bằng

A. \({a^3}\sqrt 6 \)   

B.  \(\frac{{{a^3}}}{3}\)     

C.  \(\frac{{{a^3}\sqrt 6 }}{2}\)   

D.  \({a^3}\)

Câu 48. Cho khối chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, góc SAC bằng \({45^0}\). Diện tích xung quanh của hình nón ngoại tiếp hình chóp S.ABCD bằng

A. \(\pi {a^2}\sqrt 2 \)                        

B. \({a^2}\sqrt 2 \)                             

C. \(\pi \frac{{{a^2}\sqrt 2 }}{2}\)                       

D. \(\pi \frac{{{a^2}\sqrt 2 }}{3}\)

Câu 49. Cho một hình cầu \(\left( S \right)\). Mặt phẳng \(\left( P \right)\)cắt hình cầu theo một hình tròn có chu vi \(2,4\pi a\). Khoảng cách từ tâm mặt cầu đến \(\left( P \right)\) bằng 1,6a. Diện tích mặt cầu và thể tích của khối cầu lần lượt là

A. \(\pi {a^2}\sqrt 2 ,\,\,\frac{{32}}{3}\pi {a^3}\)               

B. \(\pi {a^2}\sqrt 2 ,\,\,\frac{8}{3}\pi {a^3}\)           

C. \(16\pi {a^2},\,\,\frac{{32}}{3}\pi {a^3}\)          

D. \(\frac{{\pi {a^2}\sqrt 2 }}{2},\,\,\frac{{32}}{3}\pi {a^3}\)

Câu 50. Cho một hình trụ có bán kính R = a. mặt phẳng \(\left( P \right)\) đi qua trục và cắt hình trụ theo một thiết diện có diện tích bằng \(6{a^2}\). Diện tích xung quanh của hình trụ và thể tích của khối trụ lần lượt là

A. \(8\pi {a^2},\,\,3\pi {a^3}\)                       

B. \(6\pi {a^2},\,\,6\pi {a^3}\)           

C. \(6\pi {a^2},\,\,3\pi {a^3}\)

D. \(6\pi {a^2},\,\,9\pi {a^3}\)

 ....................................

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 3

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 3)

Câu 1 : Đường thẳng nào cho dưới đây là tiệm cận ngang của đồ thị hàm số  $y={\displaystyle \frac{2x-3}{x+1}}$.

A.  $y=-2$.

B.  $y=-1$.

C.  $x=2$.

D.  $y=2$.

Câu 2 : Cho hàm số  $f\left(x\right)=x^2\ln x$. Tính  $f^{\prime }\left(e\right)$.

A.  $3e$.

B.  $2e$.

C.  $e$.

D.  $2+e$.

Câu 3 : Viết công thức tính  $V$ của khối cầu có bán kính  $r$.

A.  $V={\displaystyle \frac{4}{3}}\pi r^3$.

B.  $V={\displaystyle \frac{1}{3}}\pi r^3$.

C.  $V=\pi r^3$.

D.  $V=4\pi r^2$.

Câu 4 : Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng 6 gần bằng số nào sau đây nhất?

A. 48.

B. 46.

C. 52.

D. 51.

Câu 5 : Tìm tập xác định D của hàm số  $y=\ln \left(x^2-3x\right)$.

A.  $D=\left(0;3\right)$.

B.  $D=\left[0;3\right]$.

C.  $D=\left(-\mathrm{\infty };0\right)\cup \left(3;+\mathrm{\infty }\right)$.

D.  $D=\left(-\mathrm{\infty };0\right)\cup \left[3;+\mathrm{\infty }\right)$.

Câu 6 : Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h). Tính thể tích của khối chóp đó.

A.  $V={\displaystyle \frac{\sqrt{3}}{4}}\left(b^2-h^2\right)h$.

B.  $V={\displaystyle \frac{\sqrt{3}}{12}}\left(b^2-h^2\right)h$.

C.  $V={\displaystyle \frac{\sqrt{3}}{8}}\left(b^2-h^2\right)h$.

D.  $V={\displaystyle \frac{\sqrt{3}}{4}}\left(b^2-h^2\right)b$.

Câu 7 : Cho hàm số  $y=x^3-mx+1$ (với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

A.  $m\le {\displaystyle \frac{3\sqrt[3]{2}}{2}}$.

B.  $m>{\displaystyle \frac{3\sqrt[3]{2}}{2}}$.

C.  $m<{\displaystyle \frac{3\sqrt[3]{2}}{2}}$.

D.  $m\ge {\displaystyle \frac{3\sqrt[3]{2}}{2}}$.

Câu 8 : Nếu tăng chiều cao một khối chóp lên 2 lần và giảm diện tích đáy đi 6 lần thì thể tích khối chóp đó tăng hay giảm bao nhiêu lần?

A. Giảm 12 lần.

B. Tăng 3 lần.

C. Giảm 3 lần.

D. Không tăng, không giảm.

Câu 9 : Cho hàm số  $y=f\left(x\right)$ có bảng biến thiên như sau:

 

Tìm tất cả các giá trị của tham số m để phương trình  $f\left(x\right)=m$ có ba nghiệm thực phân biệt.

A.  $m\in \left(-1;+\mathrm{\infty }\right)$.

B.  $m\in \left(-\mathrm{\infty };3\right)$.

C.  $m\in \left(-1;3\right)$.

D.  $m\in \left[-1;3\right]$.

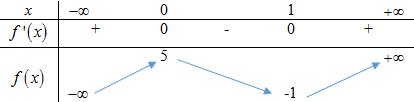
Câu 10 : Cho hàm số  $y=f\left(x\right)$ có bảng biến thiên như hình bên. Mệnh đề nào sau đây đúng?

A. Hàm số có điểm cực tiểu bằng 0.

B. Hàm số có điểm cực đại bằng 5.

C. Hàm số có điểm cực tiểu bằng -1.

D. Hàm số có điểm cực tiểu bằng 1.

                                    

Câu 11 : Cho a là số thực dương khác 1. Mệnh đều nào dưới đây đúng với mọi số dương x, y.

A.  ${\log }_a\left(xy\right)={\log }_{a}x+{\log }_{a}y$  

B.  ${\log }_a\left(xy\right)={\log }_a\left(x+y\right)$.

C.  ${\log }_a\left(xy\right)={\log }_a\left(x-y\right)$.

D.  ${\log }_a\left(xy\right)={\log }_{a}x.{\log }_{a}y$.

Câu 12 : Cho hàm số  $y={\displaystyle \frac{x-2}{\sqrt{4x^2-1}}}$ có đồ thị  $\left(C\right)$. Đồ thị  $\left(C\right)$ có bao nhiêu đường tiệm cận?

A. 4.

B. 3.

C. 1.

D. 2.

Câu 13 : Tính thể tích khối hộp chữ nhật  $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ có  $AB=3,AD=4,A{A}^{\prime }=5$.

A.  $V=12$.

B.  $V=60$.

C.  $V=10$.

D.  $V=20$.

Câu 14 : Cho hàm số  $y={\displaystyle \frac{1}{3}}{x}^3-2x^2+2x+1\left(C\right)$. Biết đồ thị  $\left(C\right)$ có hai tiếp tuyến cùng vuông góc với đường thẳng  $d:y=x$. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.

A.  $h=\sqrt{2}$.

B.  $h={\displaystyle \frac{4\sqrt{2}}{3}}$.

C.  $h={\displaystyle \frac{\sqrt{2}}{3}}$.

D.  $h={\displaystyle \frac{2\sqrt{2}}{3}}$.

Câu 15 : Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp.

A.  $V={\displaystyle \frac{a^3\sqrt{3}}{2}}$.

B.  $V={\displaystyle \frac{a^3\sqrt{3}}{3}}$.

C.  $V={\displaystyle \frac{a^3\sqrt{3}}{12}}$.

D.  $V={\displaystyle \frac{a^3\sqrt{3}}{6}}$.

Câu 16 : Cho khối tứ diện  $ABCD$, M là trung điểm của AB. Mặt phẳng (MCD) chia khối tứ diện  $ABCD$ thành hai khối đa diện nào?

A. Hai khối lăng trụ tam giác.

B. Hai khối chóp tứ giác.

C. Một khối lăng trụ tam giác và một khối tứ diện

D. Hai khối tứ diện.               

Câu 17 : Tìm số giao điểm của đồ thị hàm số  $y=\left(x-1\right)\left(x^2-2x\right)$ với trục hoành.

A. 1.

B. 2.

C. 0.

D. 3.

Câu 18 : Cho hàm số  $y=x^3+3x^2-9x+1$. Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng  $\left(-3;1\right)$.

B. Hàm số đồng biến trên khoảng  $\left(-3;1\right)$.

C. Hàm số nghịch biến trên khoảng  $\left(1;+\mathrm{\infty }\right)$.

D. Hàm số nghịch biến trên khoảng  $\left(-\mathrm{\infty };-3\right)$.

Câu 19 : Cho  $a>0$. Hãy viết biểu thức  ${\displaystyle \frac{a^4.\sqrt[4]{a^5}}{\sqrt[3]{a\sqrt{a}}}}$ dưới dạng lũy thừa với số mũ hữu tỉ?

A.  $a^{{\displaystyle \frac{9}{2}}}$.

B.  $a^{{\displaystyle \frac{19}{4}}}$.

C.  $a^{{\displaystyle \frac{23}{4}}}$.

D.  $a^{{\displaystyle \frac{3}{4}}}$.

Câu 20 : Tìm giá trị nhỏ nhất của hàm số  $y=x^3-3x^2-9x+2$ trên đoạn  $\left[0;4\right]$.

A.  $\underset{\left[0;4\right]}{min}y=-18$.

B.  $\underset{\left[0;4\right]}{min}y=2$.

C.  $\underset{\left[0;4\right]}{min}y=-25$.

D.  $\underset{\left[0;4\right]}{min}y=-34$.

Câu 21 : Một hình trụ có bán kính đáy  $r=5cm$, chiều cao  $h=7cm$. Tính diện tích xung quanh của hình trụ.

A.  $S_{xq}=35\pi \left(c{m}^2\right)$.

B.  $S_{xq}=70\pi \left(c{m}^2\right)$.

C.  $S_{xq}={\displaystyle \frac{35}{3}}\pi \left(c{m}^2\right)$.

D.  $S_{xq}={\displaystyle \frac{70}{3}}\pi \left(c{m}^2\right)$.

Câu 22 : Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

A.  $y=x^4-3x^2-1$.

B.  $y=-x^3+3x-1$.                                             

C.  $y=x^4-3x^2+1$.

D.  $y=x^3-2x^2+1$.

Câu 23 : Cho tứ diện $ABCD$ có  $DA$ vuông góc với  $\left(ABC\right)$ và  $AD=a,AC=2a$; cạnh  $BC$ vuông góc với cạnh  $AB$. Tính bán kính  $r$ của mặt cầu ngoại tiếp tứ diện $ABCD$.

A.  $r=a\sqrt{5}$.

B.  $r={\displaystyle \frac{a\sqrt{3}}{2}}$.

C.  $r=a$.

D.  $r={\displaystyle \frac{a\sqrt{5}}{2}}$.

Câu 24 : Cho khối chóp  $S.ABCD$ có đáy là hình chữ nhật cạnh $AB=2a,AD=a$. Hình chiếu của đỉnh  $S$ lên đáy là trung điểm của  $AB$, cạnh bên  $SC$ tạo với đáy một góc  ${45}^{\circ }$. Tính thể tích  $V$ của khối chóp đã cho.

A.  $V={\displaystyle \frac{2\sqrt{2}{a}^3}{3}}$.

B.  $V={\displaystyle \frac{\sqrt{3}{a}^3}{6}}$.

C.  $V=2\sqrt{2}{a}^3$.

D.  $V={\displaystyle \frac{\sqrt{2}{a}^3}{3}}$.

Câu 25 : Cho khối chóp  $S.ABC$ có  $SA,SB,SC$ đôi một vuông góc với nhau và  $SA=a,SB=b,SC=c$. Tính thể tích khối chóp  $S.ABC$.

A.  $V={\displaystyle \frac{1}{6}}abc$.

B.  $V={\displaystyle \frac{1}{3}}abc$.

C.  $V=abc$.

D.  $V={\displaystyle \frac{1}{2}}abc$.

Câu 26 : Gọi S là tập nghiệm của phương trình  $2^{2x-1}-{5.2}^{x-1}+3=0$. Tìm  $S$.

A.  $S=\left\{1;{\log }_{2}3\right\}$.

B.  $S=\left\{0;{\log }_{2}3\right\}$.

C.  $S=\left\{1;{\log }_{3}2\right\}$.

D.  $S=\left\{1\right\}$.

Câu 27 : Đồ thị hàm số nào dưới đây đi qua điểm  $M\left(2;-1\right)$?

A.  $y=-x^3+3x-1$.

B.  $y=x^4-4x^2+1$.

C.  $y={\displaystyle \frac{2x-3}{x-3}}$.

D.  $y={\displaystyle \frac{-x+3}{x+1}}$.

Câu 28 : Viết công thức diện tích xung quanh  $S_{xq}$ của hình nón tròn xoay có độ lại đường sinh l và bán kính đường tròn đáy r.

A.  $S_{xq}=2\pi rl$.

B.  $S_{xq}=rl$.

C.  $S_{xq}=\pi rl$.

D.  $S_{xq}={\displaystyle \frac{1}{2}}\pi rl$.

Câu 29: Cho hàm số  $y={\displaystyle \frac{2x+1}{x-1}}$. Phương trình tiếp tuyến tại điểm  $M\left(2;5\right)$ của đồ thị hàm số trên là:

A.  $y=3x-11$.

B.  $y=-3x+11$.

C.  $y=-3x-11$.

D.  $y=3x+11$

Câu 30 : Tìm tập xác định D của hàm số  $y={\left(3x-1\right)}^{{\displaystyle \frac{1}{3}}}$.

A.  $D=\left[{\displaystyle \frac{1}{3}};+\mathrm{\infty }\right)$.

B.  $D=R$.

C.  $D=R\mathrm{\setminus }\left\{{\displaystyle \frac{1}{3}}\right\}$.

D.  $D=\left({\displaystyle \frac{1}{3}};+\mathrm{\infty }\right)$.

Câu 31 : Cho đồ thị hàm số  $\left(C\right):y=x^3-3x$. Mệnh đề nào dưới đây sai?

A. Đồ thị  $\left(C\right)$ nhận gốc tọa độ O làm tâm đối xứng.                         

B. Đồ thị  $\left(C\right)$ cắt trục tung tại 1 điểm.    

C. Đồ thị  $\left(C\right)$ nhận trục Oy làm trục đối xứng.                                 

D. Đồ thị  $\left(C\right)$ cắt trục hoành tại 3 điểm phân biệt.

Câu 32 : Tính đạo hàm của hàm số  $y=3^x$.

A.  $y^{\prime }={\displaystyle \frac{1}{\ln 3}}{.3}^x$.

B.  $y^{\prime }=3^x$.

C.  $y^{\prime }=3^x.\ln 3$.

D.  $y^{\prime }=x{.3}^{x-1}$.

Câu 33 : Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:

A. Mỗi cạnh là cạnh chung của ít nhất ba mặt.

 B. Mỗi mặt có ít nhất ba cạnh.

C. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.

 D. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.

Câu 34 : Cho hình hộp chữ nhật  $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ có tâm  $I$. Gọi  $V,V_1$ lần lượt là thể tích của khối hộp  $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ và khối chóp  $I.ABCD$. Tính tỉ số  $k={\displaystyle \frac{V_1}{V}}$.

A.  $k={\displaystyle \frac{1}{6}}$.

B.  $k={\displaystyle \frac{1}{3}}$.

C.  $k={\displaystyle \frac{1}{8}}$.

D.  $k={\displaystyle \frac{1}{12}}$.

Câu 35 : Bảng sau là bảng biến thiên của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

 

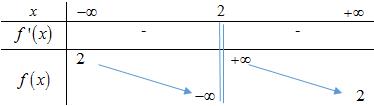
A.  $y={\displaystyle \frac{x+1}{x-2}}$.

B.  $y={\displaystyle \frac{2x-1}{x+2}}$.

C.  $y={\displaystyle \frac{2x+3}{x-2}}$.

D.  $y={\displaystyle \frac{x-4}{x-2}}$.

Câu 36 : Tính tổng lập phương các nghiệm của phương trình:  ${\log }_{2}x.{\log }_{3}x+1={\log }_{2}x+{\log }_{3}x$.

A. 125.

B. 35.

C. 13.

D. 5.

Câu 37 : Tìm giá trị lớn nhất của hàm số  $y={\displaystyle \frac{x}{x^2+4}}$ trên đoạn  $\left[1;5\right]$.

A.  $\underset{\left[1;5\right]}{max}y={\displaystyle \frac{5}{29}}$.

B.  $\underset{\left[1;5\right]}{max}y={\displaystyle \frac{1}{4}}$.

C.  $\underset{\left[1;5\right]}{max}y={\displaystyle \frac{\sqrt{2}}{6}}$.

D.  $\underset{\left[1;5\right]}{max}y={\displaystyle \frac{1}{5}}$.

Câu 38 : Tìm tất cả các giá trị thực của tham số m để hàm số  $y=-x^3+2x^2-\left(m-1\right)x+2$ nghịch biến trên khoảng  $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

A.  $m\le {\displaystyle \frac{7}{3}}$.

B.  $m\ge {\displaystyle \frac{7}{3}}$.

C.  $m\ge {\displaystyle \frac{1}{3}}$.

D.  $m>{\displaystyle \frac{7}{3}}$.

Câu 39 : Cho hàm số  $y={\displaystyle \frac{x+1}{x-1}}$. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn  $\left[-5;-1\right]$. Tính  $M+m$.

A.  $-6$.

B.  ${\displaystyle \frac{2}{3}}$.

C.  ${\displaystyle \frac{3}{2}}$.

D.  ${\displaystyle \frac{6}{5}}$.

Câu 40 : Cho lăng trụ đứng  $ABC.A_1{B}_1{C}_1$ có đáy  $ABC$ là tam giác vuông cân tại  $C,AC=a\sqrt{2}$. Biết tam giác  $AB{C}_1$ có chu vi bằng  $5a$. Tính thể tích  $V$ của khối lăng trụ  $ABC.A_1{B}_1{C}_1$.

A.  $V={\displaystyle \frac{a^3}{3}}$.

B.  $V={\displaystyle \frac{a^3\sqrt{3}}{2}}$.

C.  $V=a^3$.

D.  $V={\displaystyle \frac{a^3}{2}}$.

Câu 41 : Trong các hàm số sau, hàm số nào đồng biến trên  $\mathbb{R}$?

A.  $y={\left({\displaystyle \frac{2}{3}}\right)}^x$.

B.  $y={\left({\displaystyle \frac{2}{\sqrt{3}}}\right)}^x$.

C.  $y={\left(0,99\right)}^x$

D.  $y={\left(2-\sqrt{3}\right)}^x$.

Câu 42 : Tìm điểm cực đại của đồ thị hàm số  $y={\displaystyle \frac{2}{3}}{x}^3-{\displaystyle \frac{5}{2}}{x}^2+2x+1$.  

A.  $M\left(2;{\displaystyle \frac{1}{3}}\right)$.

B.  $M\left(2;{\displaystyle \frac{-1}{3}}\right)$.

C.  $M\left({\displaystyle \frac{1}{2}};-{\displaystyle \frac{35}{24}}\right)$.

D.  $M\left({\displaystyle \frac{1}{2}};{\displaystyle \frac{35}{24}}\right)$.

Câu 43 : Đặt  $a={\log }_{3}45$. Mệnh đề nào dưới đây đúng?

A.  ${\log }_{45}5={\displaystyle \frac{a+2}{a}}$.

B.  ${\log }_{45}5={\displaystyle \frac{a-1}{a}}$.

C.  ${\log }_{45}5={\displaystyle \frac{2-a}{a}}$.

D.  ${\log }_{45}5={\displaystyle \frac{a-2}{a}}$.

Câu 44 : Tính  $\underset{x\to 0}{lim}{\displaystyle \frac{e^{2017x}-1}{x}}$.

A. 0.

B. 1.

C. 2017.

D.  $+\mathrm{\infty }$.

Câu 45 : Tìm giá trị cực tiểu  $y_{CT}$ của hàm số  $y=x^4-4x^2+3$.

A.  $y_{CT}=0$.

B.  $y_{CT}=\sqrt{2}$.

C.  $y_{CT}=3$.

D.  $y_{CT}=-1$.

Câu 46 : Tìm nghiệm của phương trình  ${\log }_2\left(2x-1\right)=3$.

A.  $x=8$.

B.  $x={\displaystyle \frac{7}{2}}$.

C.  $x={\displaystyle \frac{9}{2}}$.

D.  $x=5$.

Câu 47 : Ông A gửi vào ngân hàng 100 triệu đồng theo hình thức lãi suất kép. Lãi suất ngân hàng là 8% trên năm và không thay đổi qua các năm ông gửi tiền. Sau 5 năm ông cần tiền sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa số tiền đó vào công việc, số còn lại ông tiếp tục gửi ngân hàng và với hình thức như trên. Hỏi sau 10 năm ông A đã thu được số tiền lãi là bao nhiêu? (đơn vị tính là triệu đồng).

A.  $\approx 79,412$.

B.  $\approx 80,412$.

C.  $\approx 81,412$.

D.  $\approx 100,412$.

Câu 48 : Cho hàm số  $f\left(x\right)$ có đạo hàm  $f^{\prime }\left(x\right)={\left(x+1\right)}^2\left(x-3\right)$. Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực đại tại  $x=3$.

B. Hàm số đạt cực tiểu tại  $x=3$.

C. Hàm số đạt cực tiểu tại  $x=-1$.

D. Hàm số đạt cực đại tại  $x=-1$.

Câu 49 : Đồ thị hàm số  $y={\displaystyle \frac{1-2x^2}{x^2+6x+9}}$ có tiệm cận đứng  $x=a$ và tiệm cận ngang  $y=b$. Tính giá trị  $T=2a-b$.

A.  $T=-4$.

B.  $T=-8$.

C.  $T=-1$.

D.  $T=-6$.

Câu 50 : Hàm số nào sau đây đồng biến trên khoảng  $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$?

A.  $y=x^4+3x$.

B.  $y=x^3+1$.             

C.  $y={\displaystyle \frac{x-1}{x+2}}$.

D.  $y=e^{-x}$.

Lời giải chi tiết

1. D	2. A	3. A	4. D	5. C
6. A	7. B	8. C	9. C	10. D
11. A	12. A	13. B	14. D	15. D
16. D	17. D	18. A	19. B	20. C
21. B	22. C	23. D	24. A	25. A
26. A	27. C	28. C	29. B	30. D
31. C	32. C	33. A	34. A	35. C
36. B	37. B	38. B	39. B	40. D
41. B	42. D	43. D	44. C	45. D
46. C	47. C	48. B	49. A	50. B

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 4

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 4)

Câu 1 : Đồ thị sau đây là của hàm số $y=x^3-3x^{}+1$. Với giá trị nào của m thì phương trình $x^3-3x-m=0$có ba nghiệm phân biệt?

A. $-1<m<3.$

B. $-2<m<2.$

C. $-2\le m<2.$

D. $-2<m<3.$

Câu 2 : Cho hàm số $y=f(x)$ có đạo hàm $f^{\prime }(x)=x^2(x+1{)}^2(2x-1)$. Khi đó số điểm cực trị của hàm số đã cho là bao nhiêu?

A. 1.

B. 2.

C. 3.

D. 0.

Câu 3 : Hàm số $y=-x^3+3x^2+5$ đồng biến trên khoảng

A. $(2;+\mathrm{\infty })$.

B. $(0;2)$.

C. $(-\mathrm{\infty };0)$.

D. $(-\mathrm{\infty };0),(2;+\mathrm{\infty })$.

Câu 4 : Giá trị của m để hàm số $y=x^3-3m{x}^2+3(m^2-1)x+m$ đạt  cực đại tại x = 1 là

A. $m=-1$.

B. $m=-2$.

C. $m=2$.

D. $m=0$.

Câu 5 : Tập hợp tất cả các số thực m để hàm số $y=x^3+5x^2-4mx-3$ đồng biến trên R là

A. $\left(-{\displaystyle \frac{25}{12}};+\mathrm{\infty }\right)$.

B. $\left[-{\displaystyle \frac{25}{12}};+\mathrm{\infty }\right)$.

C. $\left(-\mathrm{\infty };-{\displaystyle \frac{25}{12}}\right)$.

D. $\left(-\mathrm{\infty };-{\displaystyle \frac{25}{12}}\right]$.

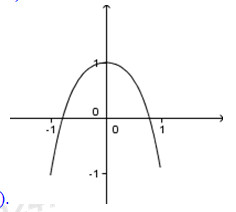
Câu 6 : Đồ thị hàm số trong hình bên dưới là đồ thị của hàm số nào?

A. $y=x^4+x^2+1$.

B. $y=-x^4+x^2+1$.

C. $y=-x^4-x^2+1$.

D. $y=x^4-x^2+1$. 

Câu 7 : Hàm số nào sau đây có cực đại, cực tiểu và $x_{CT}<$ x­_CĐ?

A. $y=-x^3-3x-2$.

B. $y=-x^3+9x^2+3x+2$.

C. $y=x^3+2x^2+8x+2$.

D. $y=x^3-9x^2-3x+5$.

Câu 8 : Cho hàm số $y=f(x)=-x^3+3x-2$. Các giá trị cực đại và cực tiểu của hàm số là

A. $y_{CD}=0;y_{CT}=-4$.

B. $y_{CD}=4;y_{CT}=-4$.

C. $y_{CD}=0;y_{CT}=4$.

D. $y_{CD}=0;y_{CT}=-6$.

Câu 9 : Hàm số$y={\displaystyle \frac{x+1}{x-1}}$

A. đồng biến trên từng khoảng xác định.

B. nghịch biến trên$R\mathrm{\setminus }\left\{1\right\}$.

C. đồng biến trên  $(-\mathrm{\infty };+\mathrm{\infty })$.

D. nghịch biến trên từng khoảng xác định.

Câu 10 : Phương trình tiếp tuyến của đồ thị hàm số $y=x^4-6x^2+8x-2$ tại điểm $x_0=1$ là

A. $y=x.$

B. $y=1.$

C. $y=x-1.$

D. $y=x+1.$

Câu 11 : Tích các giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=x^3-3x+1$trên [0; 1] là

A. $-3.$

B. $3.$

C. $1.$

D. $-1$.

Câu 12 : Cho hàm số $y=f\left(x\right)$ có bảng biến thiên là

 

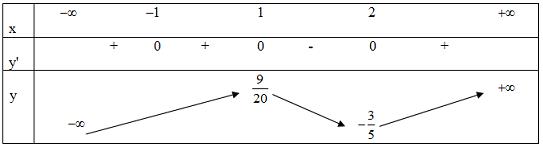
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có ba cực trị.

B. Hàm số có giá trị lớn nhất bằng ${\displaystyle \frac{9}{20}}$ và giá trị nhỏ nhất bằng $-{\displaystyle \frac{3}{5}}.$

C. Hàm số đồng biến trên khoảng $\left(-\mathrm{\infty };1\right).$

D. Hàm số đạt cực đại tại $x=2$ và đạt cực tiểu tại $x=1.$

Câu 13 : Giá trị nhỏ nhất của hàm số $y=x-\sqrt{16-x^2}$ là

A. $-5$.

B. $-5\sqrt{2}$.

C. $-4$.

D. $-4\sqrt{2}$.

Câu 14 : Đồ thị của hàm số$y={\displaystyle \frac{2x^2-8}{x^2-3x+2}}$ có bao nhiêu đường tiệm cận?

A. 2.

B. 1.

C. 3.

D. 0.

Câu 15 : Cho x, y là hai số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?

A. $x^m.x^n=x^{m+n}.$

B. $x^m.y^n={\left(xy\right)}^{m+n}.$

C. $x^m.y^m={\left(xy\right)}^m.$

D. $x^m:x^n=x^{m-n}.$

Câu 16 : Cho x là số thực dương. Dạng lũy thừa với số mũ hữu tỉ của biểu thức $\sqrt{x.\sqrt[3]{x}}$ là

A. $x^{{\displaystyle \frac{1}{12}}}$.

B. $x^{{\displaystyle \frac{1}{3}}}$.

C. $x^{{\displaystyle \frac{2}{3}}}$.

D. $y=x^{{\displaystyle \frac{5}{6}}}$.

Câu 17 : Cho hàm số $y=(2x^2+4x+1{)}^{\sqrt{3}}$. Khi đó đạo hàm $y^{\prime }(0)$ bằng

A. $4\sqrt{3}.$

B. $0.$

C. $12\sqrt{3}.$

D. $28\sqrt{3}.$

Câu 18 : Đạo hàm y’(x) của hàm số $y=x.\ln \mathrm{x}$là

A.  $1+{\displaystyle \frac{1}{x}}.$

B. $1+\ln \mathrm{x}.$

C. $1+x.$

D. $1-x.$

Câu 19 : Tập xác định của hàm số $y={\log }_2(x^2-3x+2)$ là

A. $R\mathrm{\setminus }\left[1;2\right]$

B. $\left(1;2\right)$

C. $\left[1;2\right]$

D. $R\mathrm{\setminus }\left(1;2\right)$

Câu 20 : Biết .. thì $\log \sqrt[4]{{\displaystyle \frac{32}{5}}}$ bằng

A. ${\displaystyle \frac{1}{4}}\left(a^6-1\right)$ .                                

B. ${\displaystyle \frac{1}{4}}\left(5a-1\right)$.

C. ${\displaystyle \frac{1}{4}}\left(6a+1\right)$.

D. ${\displaystyle \frac{1}{4}}\left(6a-1\right)$.

Câu 21 : Gọi các nghiệm của phương trình $4^{x+1}-6.2^{x+1}+8=0$ là $x_1,x_2$. Khi đó $x_1^2+x_2^2$ bằng

A. 0.

B. 1.

C. 3.

D. $2$.

Câu 22 : Hàm số $f\left(x\right)=x^2\ln x$ đạt cực trị tại điểm

A. $x={\displaystyle \frac{1}{\sqrt{e}}}.$

B. $x=\sqrt{e}.$

C. $x=e$

D. $x={\displaystyle \frac{1}{e}}.$

Câu 23 : Tập nghiệm của phương trình ${\log }_3(9^x+8)=x+2$ là

A. $\left\{0\right\}$

B. $\left\{1;8\right\}$ .

C. $\left\{0;\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}4\right\}$ .

D. $\left\{0;\mathrm{l}\mathrm{o}{\mathrm{g}}_{3}8\right\}$.

Câu 24 : Tập nghiệm của bất phương trình ${\log }_3\left(2x-1\right)>3$ là:

A. $\left(5;+\mathrm{\infty }\right)$

B. $\left(14;+\mathrm{\infty }\right)$

C. $\left(-\mathrm{\infty };2\right)$

D. $\left({\displaystyle \frac{1}{2}};14\right)$.

Câu 25 : Một khối chóp có đáy là hình vuông cạnh a và các cạnh bên cùng bằng ${\displaystyle \frac{a\sqrt{6}}{2}}$. Khi đó thể tích của khối chóp là

A. ${\displaystyle \frac{a^3}{2}}$.

B. ${\displaystyle \frac{a^3}{3}}$.

C. ${\displaystyle \frac{a^3}{4}}$.

D. ${\displaystyle \frac{a^3}{6}}$.

Câu 26 : Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy  bằng ${60}^0$. Thể tích khối chóp là

A. ${\displaystyle \frac{\sqrt{3}{a}^3}{6}}.$

B. ${\displaystyle \frac{\sqrt{6}{a}^3}{3}}.$

C. ${\displaystyle \frac{\sqrt{6}{a}^3}{6}}.$

D. ${\displaystyle \frac{\sqrt{2}{a}^3}{6}}.$

Câu 27 : Cho hình chóp S.ABCD có $SA\mathrm{\perp }(ABCD)$, ABCD là hình chữ nhật với AB = a, BC=2a và SA = 3a. Thể tích của khối cầu ngoại tiếp hình chóp là

A. $V={\displaystyle \frac{56\pi a^2}{3}}$.

B. $V={\displaystyle \frac{56\pi \sqrt{14}.a^3}{3}}$.

C. $V={\displaystyle \frac{7\pi \sqrt{14}.a^3}{3}}$.

D. $V={\displaystyle \frac{14\pi \sqrt{4}.a^3}{3}}$.

Câu 28 : Khối lập phương ABCD.A’B’C’D’ có độ dài đoạn $A{B}^{\prime }=2a$. Thể tích của khối đó là

A. $2\sqrt{2}{a}^3.$

B. $8a^3.$

C. $3\sqrt{3}{a}^3.$

D. $3\sqrt{2}{a}^3.$

Câu 29 : Khẳng định nào sau đây là sai?

A. Mọi hình chóp đều luôn có mặt cầu ngoại tiếp.

B. Mọi tứ diện luôn có mặt cầu ngoại tiếp.

C. Mọi hình chóp luôn có mặt cầu ngoại tiếp.

D. Mọi hình hộp chữ nhật luôn có mặt cầu ngoại tiếp.

Câu 30 : Cho tứ diện SABC có SA = 4a và SA vuông góc với mặt phẳng (ABC). Tam giác ABC vuông tại B, có AB = a, BC= 3a. Diện tích mặt cầu ngoại tiếp tứ diện SABC bằng

A. $100\pi a^2.$

B. $104\pi a^2.$

C. $102\pi a^2.$

D. $26\pi a^2.$

Câu 31 : Hình lăng trụ đứng ABC.A’B’C’, đáy là tam giác ABC vuông tại A, có AB = a, BC = 2a, góc giữa AC’ và mặt phẳng đáy bằng ${60}^0$. Hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ có diện tích toàn phần là

A. $3\sqrt{3}\pi a^2.$

B. $6\pi a^2.$

C. $7\pi a^2.$

D. $8\pi a^2$.

Câu 32 : Một mặt cầu $(S)$ cắt mặt phẳng kính của nó theo đường tròn có bán kính là 5. Diện tích mặt cầu (S) là

A. $100\pi .$

B. ${\displaystyle \frac{500\pi }{3}}.$

C. $20\pi .$

D. $10\pi$.

Câu 33 : Cho hình nón có bán kính đáy bằng a, đường sinh có độ dài bằng $a\sqrt{3}$. Thể tích của khối nón đó là

A. $\pi \sqrt{2}.a^3$.

B. ${\displaystyle \frac{\pi \sqrt{3}.a^3}{3}}$.

C. ${\displaystyle \frac{\pi \sqrt{2}.a^3}{2}}$ .

D. ${\displaystyle \frac{\pi \sqrt{2}.a^3}{3}}$.

Câu 34 : Cho lăng trụ đứng tam giác ABC.A’B’C’, đáy là tam giác vuông tại A, $AC=a,\widehat{ACB}={60}^o,A{C}^{\prime }=3a.$ Thể tích khối lăng trụ đó là

A. ${\displaystyle \frac{4a^3.\sqrt{6}}{3}}$.

B. $\sqrt{6}.a^3$ .

C. ${\displaystyle \frac{2a^3.\sqrt{6}}{3}}$.

D. ${\displaystyle \frac{a^3.\sqrt{6}}{3}}$.

Câu 35 : Tập xác định của hàm số $f\left(x\right)=\sqrt{1-\ln \left(2x-1\right)}$ là

A. $\left[{\displaystyle \frac{1}{2}};{\displaystyle \frac{e+1}{2}}\right]$.

B. $\left({\displaystyle \frac{1}{2}};{\displaystyle \frac{e+1}{2}}\right)$.

C. $\left({\displaystyle \frac{1}{2}};{\displaystyle \frac{e+1}{2}}\right]$.

D. $\left[{\displaystyle \frac{1}{2}};{\displaystyle \frac{e+1}{2}}\right)$.

Câu 36 : Đồ thị hàm số $y=x+3+\sqrt{x^2+x+1}$

A. có tiệm cận đứng $x=-3$.

B. có tiệm cận ngang $y={\displaystyle \frac{5}{2}}$.

C. có tiệm cận ngang $y=-3$.

D. không có tiệm cận ngang.

Câu 37 : Cho hàm số $y={\displaystyle \frac{2x+1}{x+1}}$ có đồ thị (C). Tiếp tuyến của (C) cắt hai tiệm cận của (C) tại hai điểm A, B. Giá trị nhỏ nhất của AB là

A. $4$.

B. $2\sqrt{3}$.

C. $2\sqrt{2}$.

D. $2$.

Câu 38 : Cho hình chóp $S.ABCD$ có đường cao $SA=4a$ ; $ABCD$ là hình thang với đáy lớn AD, biết$AD=4a,AB=BC=CD=2a$. Thể tích của khối cầu ngoại tiếp hình chóp $S.ABC$ bằng

A. $64\pi a^3\sqrt{2}.$

B. ${\displaystyle \frac{64\pi a^3\sqrt{2}}{3}}.$

C. ${\displaystyle \frac{32\pi a^3\sqrt{2}}{3}}.$

D. $32\pi a^3\sqrt{2}.$

Câu 39 : Với giá trị nào của m thì phương trình ${\log }_3^{2}x-(m+2).{\log }_{3}x+3m-1=0$ có 2 nghiệm x₁, x₂ thỏa mãn x₁.x₂ = 27?

A. m = 1.

B. $m={\displaystyle \frac{28}{3}}.$

C. $m={\displaystyle \frac{4}{3}}$

D. $m=25$

Câu 40 : Tập nghiệm của bất phương trình $9^{{\displaystyle \frac{-2}{x}}}+3^{{\displaystyle \frac{-2}{x}}}>12$là

A. $\left(-\mathrm{\infty };-2\right)$

B. $\left(-2;+\mathrm{\infty }\right)$

C. $\left(-2;0\right)$

D. $\left(0;2\right)$

Câu 41 : Đồ thị của hàm số $y={\displaystyle \frac{2x-1}{\left|x\right|+1}}$ có bao nhiêu đường tiệm cận?

A. 0.

B. 1.

C. 2.

D. 3.

Câu 42 : Với giá trị thực nào của tham số m thì đồ thị hàm số $y=x^4-2m{x}^2+2m+m^4$ có ba điểm cực trị là ba đỉnh của một tam giác đều?

A. $m=0.$

B. $m=\sqrt[3]{3}.$

C. $m=-\sqrt[3]{3}.$

D. $m=1.$

Câu 43 : Cho hàm số $y=m\cot (x^2)$. Tập hợp tất cả các giá trị của m thỏa mãn $m^2-4<0$ sao cho hàm số đã cho đồng biến trên $\left(0;{\displaystyle \frac{\pi }{4}}\right)$là

A. Æ.

B. $\left(-2;2\right)\mathrm{\setminus }\left\{0\right\}.$

C. $\left(0;2\right).$

D. $\left(-2;0\right).$

Câu 44 : Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép (một quý bằng 3 tháng). Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được tính từ lần gửi ban đầu đến thời điểm sau khi gửi thêm 1 năm, gần nhất với kết quả nào sau đây?

A. 210 triệu.

B. 220 triệu.

C. 212 triệu.

D. 216 triệu.

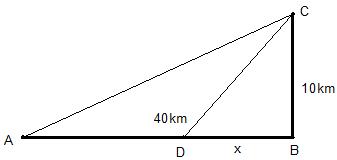
Câu 45 : Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là BC = 10km, khoảng cách từ khách sạn A đến điểm ngắn nhất tính từ đảo C vào bờ là AB = 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy từ khách sạn ra đảo (như hình vẽ dưới đây). Biết kinh phí đi đường thủy là 5 USD/km, kinh phí đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một đoạn AD bao nhiêu để kinh phí đi từ A đến C nhỏ nhất? (AB vuông góc BC-hình dưới đây)                                                                                                             

A. ${\displaystyle \frac{15}{2}}km.$

B. ${\displaystyle \frac{65}{2}}km.$

C. $10km.$

D. $40km.$

Câu 46 : Cho tứ diện ABCD, có AB=AC=AD=a, $\widehat{BA\mathrm{D}}={90}^0;\widehat{DAC}={60}^0;\widehat{CAB}={120}^0.$ Thể tích tứ diện ABCD là

A. ${\displaystyle \frac{a^3\sqrt{2}}{6}}.$

B. ${\displaystyle \frac{a^3\sqrt{2}}{12}}.$

C. ${\displaystyle \frac{a^3\sqrt{2}}{4}}.$

D. ${\displaystyle \frac{a^3\sqrt{3}}{12}}.$

Câu 47 : Cho hình chóp S.ABCD đáy ABCD là hình thoi. SA = x $\left(0<x<\sqrt{3}\right)$ các cạnh còn lại đều bằng 1. Thể tích của khối chóp S.ABCD là

A. ${\displaystyle \frac{x\sqrt{3-x^2}}{3}}.$

B. ${\displaystyle \frac{x^2\sqrt{3-x^2}}{6}}.$

C. ${\displaystyle \frac{x^2.\sqrt{3-x^2}}{3}}.$

D. ${\displaystyle \frac{x.\sqrt{3-x^2}}{6}}.$

Câu 48 : Cho hình chóp S.ABC có $SA\mathrm{\perp }(ABC)$, tam giác ABC vuông tại B. Biết $SA=a$, $AB=b,BC=c$. Gọi B’, C’ tương ứng là hình chiếu vuông góc của A trên SB, SC. Gọi V, V’ tương ứng là thể tích của các khối chóp S.ABC, S.AB’C’. Khi đó ta có

A. ${\displaystyle \frac{V^{\prime }}{V}}={\displaystyle \frac{a^2}{a^2+b^2}}$.

B. ${\displaystyle \frac{V^{\prime }}{V}}={\displaystyle \frac{a^2}{a^2+b^2+c^2}}$.

C. ${\displaystyle \frac{V^{\prime }}{V}}={\displaystyle \frac{a^4}{\left(a^2+b^2\right)\left(a^2+b^2+c^2\right)}}$.

D. ${\displaystyle \frac{V^{\prime }}{V}}={\displaystyle \frac{a^2}{a^2+b^2}}+{\displaystyle \frac{a^2}{a^2+b^2+c^2}}$.

Câu 49 : Khối tứ diện ABCD có cạnh AB = CD = a, độ dài tất cả các cạnh còn lại bằng b, (2b² > a²). Thể tích V của khối tứ diện đó là

A. ${\displaystyle \frac{1}{3}}{a}^2.\sqrt{b^2-{\displaystyle \frac{a^2}{2}}}$.

B. ${\displaystyle \frac{1}{6}}{a}^2.\sqrt{b^2-{\displaystyle \frac{a^2}{2}}}$.

C. ${\displaystyle \frac{1}{12}}{a}^2.\sqrt{b^2-{\displaystyle \frac{a^2}{2}}}$

D. ${\displaystyle \frac{1}{18}}{a}^2.\sqrt{b^2-{\displaystyle \frac{a^2}{2}}}$.

Câu 50 : Các hình trụ tròn xoay có diện tích toàn phần là S không đổi, gọi chiều cao hình trụ là h và bán kính đáy hình trụ là r. Thể tích của khối trụ đó đạt giá trị lớn nhất khi

A. $h=4r$.

B. $h=3r$

C. $h=2r$.                        

D. $h=r$.

Lời giải chi tiết

1. A	2. A	3. B	4. C	5. D
6. C	7. B	8. A	9. D	10. B
11. D	12. C	13. D	14. A	15. B
16. C	17. A	18. B	19. A	20. D
21. B	22. A	23. D	24. B	25. B
26. C	27. C	28. A	29. C	30. B
31. D	32. A	33. D	34. B	35. C
36. B	37. C	38. B	39. A	40. C
41. C	42. B	43. D	44. C	45. A
46. B	47. D	48. C	49. B	50. C

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 5

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 5)

Câu 1 .Số mặt phẳng đối xứng của hình chóp đều $S.ABC$ là

A. $4$ .

B. $2$ .

C. $6$ .

D. $3$ .

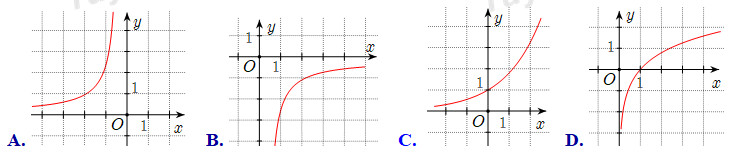
Câu 2 .Cho $a$ là số thực dương khác $1$ . Hình nào sau đây là đồ thị của hàm số mũ $y=a^x$?

Câu 3 . Khối cầu $(S)$ có bánh kính bằng $r$ và thể tích bằng $V$. Mệnh đề nào dưới đây đúng?

A. $V={\displaystyle \frac{4}{3}}\pi r^3$ .

B. $V={\displaystyle \frac{4}{3}}{\pi }^2{r}^2$.

C. $V={\displaystyle \frac{4}{3}}{\pi }^2{r}^3$.

D. $V={\displaystyle \frac{4}{3}}\pi r$.

Câu 4 . Cho ${\log }_{3}x=6$. Tính $K={\log }_3\sqrt[3]{x}$.

A. $K=4$ .

B. $K=8$.

C. $K=2$.

D. $K=3$.

Câu 5 . Cho khối chóp $S.ABCD$ có đáy là hình chữ nhật $AB=a,BC=2a$ , $SA$ vuông góc với đáy và $SC$ tạo với mặt phẳng $(SAB)$ một góc bằng ${60}^0$. Tính thể tích $V$ của khối chóp đã cho.

A. $V={\displaystyle \frac{\sqrt{6}{a}^3}{3}}$ .

B. $V=\sqrt{2}{a}^3$.

C.$V={\displaystyle \frac{\sqrt{2}{a}^3}{3}}$ .

D. $V={\displaystyle \frac{2a^3\sqrt{3}}{9}}$.

Câu 6 . Cho tứ diện $ABCD$ có tam giác $BCD$ vuông tại $B,AC$ vuông góc với mặt phẳng$\left(BCD\right)$, $AC=5a,BC=3a$ và$BD=4a$. Tính bán kính $R$ của mặt cầu ngoại tiếp tứ diện$ABCD$.

A. $R={\displaystyle \frac{5a\sqrt{3}}{2}}$.

B. $R={\displaystyle \frac{5a\sqrt{2}}{3}}$.

C. $R={\displaystyle \frac{5a\sqrt{3}}{3}}$.

D. $R={\displaystyle \frac{5a\sqrt{2}}{2}}$.

Câu 7 . Đồ thị hàm số $y=x^3+3x^2-9x-1$ có hai cực trị $A$ và $B$. Điểm nào dưới đây thuộc đường thẳng$AB$?

A. $N\left(0;2\right)$.

B. $P\left(-1;1\right)$.

C. $Q\left(-1;-8\right)$.

D. $M\left(0;-1\right)$.

Câu 8 . Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như hình bên. Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho

A. $y_{CD}=3$ và $y_{CT}=0$.                          

B. $y_{CD}=2$ và $y_{CT}=-2$.

C. $y_{CD}=-2$ và $y_{CT}=2$.

D. $y_{CD}=0$ và $y_{CT}=3$

 

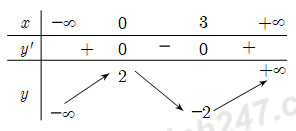
Câu 9 . Cho hình chóp $S.ABC$ có $AB=6,BC=8,AC=10$. Cạnh bên $SA$ vuông góc với đáy và $SA=4$. Tính thể tích $V$ của khối chóp $S.ABC$.

A. $V=40$.

B. $V=32$.

C. $V=192$.

D. $V=24$.

Câu 10 .  Cho $a$ là số thực dương khác 1. Mệnh đề nào dưới đây đúng với mọi số thực dương $x,y$?

A. ${\log }_a\left(xy\right)={\log }_{a}x.{\log }_{a}y$.

B. ${\log }_a\left(xy\right)={\log }_{a}x-{\log }_{a}y$

C. ${\log }_a\left(xy\right)={\displaystyle \frac{{\log }_{a}x}{{\log }_{a}y}}$.

D. ${\log }_a\left(xy\right)={\log }_{a}x+{\log }_{a}y$.

Câu 11 .  Cho hàm số $y=f\left(x\right)$ liên tục trên $\mathbb{R}$, bảng biến thiên như sau. Kết luận nào sau đây đúng.

A. Hàm số có ba điểm cực trị.        

B. Hàm số có hai điểm cực trị.

C. hàm số đạt cực tiểu tại $x=1$.

D. Hàm số đạt cực đại tại $x=2$.

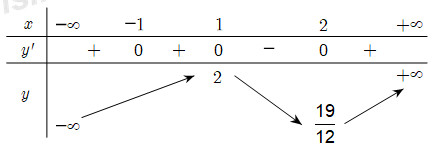
Câu 12 .  Cho $\left(S\right)$ là một mặt cầu cố định có bán kính $R$. Một hình trụ $\left(H\right)$ thay đổi nhưng luôn có hai đường tròn đáy nằm trên $\left(S\right)$. Gọi $V_1$ là thể tích của khối cầu $\left(S\right)$ và $V_2$ là thể tích lớn nhất của khối trụ $\left(H\right)$. Tính tỉ số ${\displaystyle \frac{V_1}{V_2}}$.

A. ${\displaystyle \frac{V_1}{V_2}}=\sqrt{6}$.

B. ${\displaystyle \frac{V_1}{V_2}}=2$.

C. ${\displaystyle \frac{V_1}{V_2}}=\sqrt{3}$.

D. ${\displaystyle \frac{V_1}{V_2}}=\sqrt{2}$

Câu 13 .  Cho hình nón tròn xoay có đường sinh bằng $13$ (cm), bán kính đường tròn đáy bằng $5$ (cm). Thể tích của khối nón tròn xoay là

A. $200\pi$($\mathrm{c}{\mathrm{m}}^3$).

B. $150\pi$($\mathrm{c}{\mathrm{m}}^3$).

C. $100\pi$($\mathrm{c}{\mathrm{m}}^3$).

D. $300\pi$($\mathrm{c}{\mathrm{m}}^3$).

Câu 14 .  Cho hàm số $y=\left(x+1\right)\left(x^2-2\right)$ có đồ thị $\left(C\right)$. Mệnh đề nào dưới đây đúng?

A. $\left(C\right)$không cắt trục hoành.

B. $\left(C\right)$ cắt trục hoành tại một điểm.

C. $\left(C\right)$cắt trục hoành tại ba điểm.                    

D. $\left(C\right)$cắt trục hoành tại hai điểm.

Câu 15 .  Thể tích $V$ của một khối lăng trụ có diện tích đáy bằng $B$ và chiều cao bằng $h$ là

A. $V={\displaystyle \frac{1}{3}}{B}^{2}h$.

B. $V=Bh$.

C. $V={\displaystyle \frac{1}{3}}Bh$.

D. $V={\displaystyle \frac{1}{2}}Bh$.

Câu 16 .  Phương trình $2^{3-4x}={\displaystyle \frac{1}{32}}$ có nghiệm là

A. $x=-3$.

B. $x=-2$.

C. $x=2$.                                     

D. $x=3$

Câu 17 .  Tập xác định của hàm số $y={\log }_2\left(10-2x\right)$ là

A. $\left(-\mathrm{\infty };2\right)$.

B. $\left(5;+\mathrm{\infty }\right)$.

C. $\left(-\mathrm{\infty };10\right)$.

D. $\left(-\mathrm{\infty };5\right)$

Câu 18 .  Gọi $S$ là tổng tất cả các giá trị nguyên dương của tham số $m$ sao cho hàm số $y={\displaystyle \frac{2x-m^2}{x-m-4}}$ đồng biến trên khoảng $\left(2021;+\mathrm{\infty }\right)$. Khi đó, giá trị của $S$ bằng

A. $2035144$.

B. $2035145$.

C. $2035146$.

D. $2035143$

Câu 19 .  Cho hàm số $y=x^4-2x^2$. Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng $\left(-1;1\right)$.

B. Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };-2\right)$.

C. Hàm số đồng biến trên khoảng $\left(-1;1\right)$.

D. Hàm số đồng biến trên khoảng $\left(-\mathrm{\infty };-2\right)$

Câu 20 .  Cho mặt cầu $\left(S\right)$ có tâm $O$, bán kính $r$. Mặt phẳng $\left(\alpha \right)$ cắt mặt cầu $\left(S\right)$ theo giao tuyến là đường tròn $\left(C\right)$ có bán kính $R$. Kết luận nào sau đây sai?

A. $R=\sqrt{r^2+d^2\left(O,\left(\alpha \right)\right)}$.

B. $d\left(O,\left(\alpha \right)\right)<r$.

C. Diện tích của mặt cầu là $S=4\pi r^2$.

D. Đường tròn lớn của mặt cầu có bán kính bằng bán kính mặt cầu

Câu 21 .  Với $a,b,x$ là các số thực dương thỏa mãn ${\log }_{5}x=4{\log }_{5}a+3{\log }_{5}b$, mệnh đề nào dưới đây là đúng?

A. $x=3a+4b$.

B. $x=4a+3b$.

C. $x=a^4{b}^3$.

D. $x=a^4+b^3$.

Câu 22 .  Một khối trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn đáy lần lượt bằng $h,l,r$. Khi đó công thức tính diện tích toàn phần của khối trụ là

A. $S_{tp}=2\pi r\left(l+r\right)$.

B. $S_{tp}=2\pi r\left(l+2r\right)$.

C. $S_{tp}=\pi r\left(l+r\right)$.

D. $S_{tp}=\pi r\left(2l+r\right)$.

Câu 23 .  Cho hình nón tròn xoay. Một mặt phẳng $\left(P\right)$ đi qua đỉnh $O$ của hình nón và cắt đường tròn đáy của hình nón tại hai điểm. Thiết diện được tạo thành là

A. Một tứ giác.

B. Một hình thang cân.

C. Một ngũ giác.

D. Một tam giác cân.

Câu 24 .  Cho ${\pi }^{\alpha }>{\pi }^{\beta }$ với $\alpha ,\beta \in \mathbb{R}$. Mện đề nào dưới đây là đúng?

A. $\alpha >\beta$.

B. $\alpha <\beta$.

C. $\alpha =\beta$.                      

D. $\alpha \le \beta$.

Câu 25 .  Khối đa diện nào sau đây có công thức thể tích là $V={\displaystyle \frac{1}{3}}Bh$? Biết hình đa diện đó có diện tích đáy bằng $B$ và chiều cao bằng $h$?

A. Khối chóp.

B. Khối hộp chữ nhật.

C. Khối hộp.

D. Khối lăng trụ.

Câu 26 .  Đồ thị $y={\displaystyle \frac{x-2}{\sqrt{x^2-4}}}$ có bao nhiêu tiệm cận?

A. 2.

B. 4.

C. 3.

D. 1.

Câu 27 .  Cho 4 số thực a, b, x, y với $a,b$ là các số dương và khác 1. Mệnh đề nào dưới đây đúng?

A. ${\displaystyle \frac{a^x}{a^y}}=a^{x-y}$.

B. ${\left(a^x\right)}^y=a^{x+y}$.

C. $a^x.a^y=a^{x.y}$

D. ${\left(a.b\right)}^x=a.b^x$.

Câu 28 . Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 (km), thành phố B cách bờ sông 5 (km), khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng vuông góc với bờ sông là 12 (km). Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn AM là

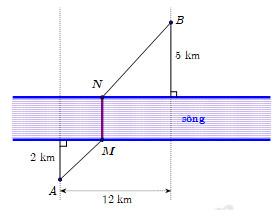
A. $AM={\displaystyle \frac{2\sqrt{193}}{7}}\mathrm{k}\mathrm{m}.$.

B. $AM={\displaystyle \frac{3\sqrt{193}}{7}}\mathrm{k}\mathrm{m}.$

C. $AM=\sqrt{193}\mathrm{k}\mathrm{m}.$

 D. $AM={\displaystyle \frac{\sqrt{193}}{7}}\mathrm{k}\mathrm{m}.$

Câu 29 .  Đạo hàm của hàm số $y=5^x+2017$ là 

A. $y^{\prime }={\displaystyle \frac{5^x}{5\ln 5}}$.

B. $y^{\prime }=5^x.\ln 5$.

C. $y^{\prime }={\displaystyle \frac{5^x}{\ln 5}}$

D. $y^{\prime }=5^x$.

Câu 30 .  Cho khối chóp $S.ABCD$ có đáy là hình vuông, $\mathrm{\Delta }SAB$ đều và nằm trong mặt phẳng vuông góc với mặt đáy. Mặt cầu ngoại tiếp khối chóp $S.ABCD$ có diện tích $84\pi \mathrm{c}{\mathrm{m}}^2$. Khoảng cách giữa hai đường thẳng $SA$ và $BD$ là

A. ${\displaystyle \frac{3\sqrt{21}}{7}}\mathrm{c}\mathrm{m}$.

B. ${\displaystyle \frac{2\sqrt{21}}{7}}\mathrm{c}\mathrm{m}$.

C. ${\displaystyle \frac{\sqrt{21}}{7}}\mathrm{c}\mathrm{m}$.

D. ${\displaystyle \frac{6\sqrt{21}}{7}}\mathrm{c}\mathrm{m}$.

Câu 31 .  Tìm tập xác định $D$ của hàm số $y={\left(x^2+x-2\right)}^{-3}$.

A. $D=\left(0;+\mathrm{\infty }\right)$.

B. $D=\left(-\mathrm{\infty };-2\right)\cup \left(1;+\mathrm{\infty }\right)$.

C. $D=\mathbb{R}\mathrm{\setminus }\left\{-2;1\right\}$.

D. $D=\mathbb{R}$.

Câu 32 .  Tìm các giá trị của tham số $m$ để hàm số $y={\displaystyle \frac{x^3}{3}}-3x^2+m^{2}x+2m-3$ đồng biến trên $\mathbb{R}$.

A. $[\begin{array}{l}m<-3\\ m>3\end{array}$.

B. $-3\le m\le 3$.

C. $-3<m<3$.

D. $[\begin{array}{l}m\le -3\\ m\ge 3\end{array}$.

Câu 33 .  Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. Với $0<a<1$, hàm số $y={\log }_{a}x$ là một hàm nghịch biến trên khoảng $\left(0;+\mathrm{\infty }\right)$.

B. Với $a>1$, hàm số $y={\log }_{a}x$ là một hàm đồng biến trên khoảng $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

C. Với $a>1$, hàm số $y=a^x$ là một hàm đồng biến trên khoảng $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

D. Với $0<a<1$, hàm số $y=a^x$ là một hàm nghịch biến trên khoảng $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

Câu 34 .  Xét các số thực dương $x,y$ thỏa mãn ${\log }_3{\displaystyle \frac{1-y}{x+3xy}}=3xy+x+3y-4$. Tìm giá trị nhỏ nhất $P_{min}$ của $P=x+y$.

A. $P_{min}={\displaystyle \frac{4\sqrt{3}+4}{3}}$.

B. $P_{min}={\displaystyle \frac{4\sqrt{3}-4}{3}}$.

C. $P_{min}={\displaystyle \frac{4\sqrt{3}-4}{9}}$.

D. $P_{min}={\displaystyle \frac{4\sqrt{3}+4}{9}}$.

Câu 35 .  Hình vẽ sau đây là đồ thị của hàm số nào ?

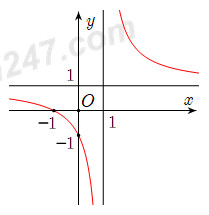
A. $y={\displaystyle \frac{x+2}{x+1}}$.

B. $y={\displaystyle \frac{x+3}{1-x}}$.                                    

C. $y={\displaystyle \frac{2x+1}{2x-1}}$.

D. $y={\displaystyle \frac{x+1}{x-1}}$.

Câu 36 .  Tính đạo hàm của hàm số $y=\log \left(2\mathrm{x}+1\right)$.

A. $y^{\prime }={\displaystyle \frac{2}{\left(2\mathrm{x}+1\right)\ln 10}}$.

B. $y^{\prime }={\displaystyle \frac{2}{\left(2\mathrm{x}+1\right)}}$.

C. $y^{\prime }={\displaystyle \frac{1}{\left(2\mathrm{x}+1\right)\ln 10}}$.

D. $y^{\prime }={\displaystyle \frac{1}{\left(2\mathrm{x}+1\right)}}$.

Câu 37 .  Mỗi cạnh của một hình đa diện là cạnh chung của đúng $n$ mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?

A. $n=2$.                                     

B. $n=5$.                                     

C. $n=3$.

D. $n=4$.

Câu 38 .  Cho hàm số $y=f\left(x\right)$ có bảng xét dấu đạo hàm như sau

 

Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };2\right)$.

B. Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };-2\right)$.

C. Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };0\right)$.

D. Hàm số nghịch biến trên khoảng $\left(-2;0\right)$.

Câu 39 .  Hình vẽ sau đây là đồ thị của hàm số nào?

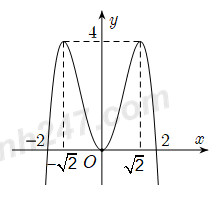
A. $y=-x^4-2x^2$

B. $y=-x^4+3x^2+1$

C. $y=-x^4+4x^2$

D. $y=x^4-3x^2$

Câu 40 .  Cho hàm số $f\left(x\right)={\displaystyle \frac{x-m^2}{x+8}},$ với $m$ là tham số. Giá trị lớn nhất của $m$ để $\underset{\left[0;3\right]}{min}f\left(x\right)=-2$ là

A. $m=5$.

B. $m=6$.

C. $m=4$.                                    

D. $m=3$.

Câu 41 .  Tìm giá trị thực của tham số $m$ để phương trình $9^x-{2.3}^{x+1}+m=0$ có hai nghiệm thực $x_1,x_2$ thỏa mãn $x_1+x_2=0$.

A. $m=6$.

B. $m=0$.                                    

C. $m=3$.                                    

D. $m=1$.

Câu 42 .  Giá trị lớn nhất của hàm số $y={\displaystyle \frac{x+4}{x-2}}$ trên đoạn $\left[3,4\right]$.

A. $-4$.

B. $10$.

C. $7$.

D. $8$.

Câu 43 .  Tìm giá trị thực của tham số $m$ để hàm số $y={\displaystyle \frac{1}{3}}{x}^3-m{x}^2+\left(m^2-4\right)x+3$ đạt cực tiểu tại $x=3$.

A. $m=1$.                                    

B. $m=-1$.

C. $m=5$.                                    

D. $m=-7$.

Câu 44 .  Cho khối lăng trụ đứng $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có đáy là tam giác cân $ABC$ với $AB=AC=a$, $\widehat{BAC}={120}^{\circ }$, mặt phẳng $\left(A{B}^{\prime }{C}^{\prime }\right)$ tạo với đáy một góc ${30}^{\circ }$. Tính thể tích $V$ của khối lăng trụ đã cho.

A. $V={\displaystyle \frac{a^3}{6}}$.

B. $V={\displaystyle \frac{a^3}{8}}$.

C. $V={\displaystyle \frac{3a^3}{8}}$.

D. $V={\displaystyle \frac{9a^3}{8}}$.

Câu 45 .  Cho khối lăng trụ đứng $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có $A{A}^{\prime }=a$, đáy $ABC$ là tam giác vuông cân tại $A$ và $BC=a\sqrt{2}$. Tính thể tích $V$ của khối lăng trụ đã cho.

A. $V=a^3$.

B. $V={\displaystyle \frac{a^3}{2}}$.

C. $V={\displaystyle \frac{a^3}{6}}$.

D. $V={\displaystyle \frac{a^3}{3}}$.

Câu 46 .  Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật $ABCD$ có $AB$ và $CD$ thuộc hái đáy của hình trụ, $AB=4a,AC=5a$. Thể tích của khối trụ.

A. $8\pi a^3$.                             

B. $12\pi a^3$.                           

C. $4\pi a^3$.                             

D. $16\pi a^3$.

Câu 47 .  Cho hình nón tròn xoay có bán kính đường tròn đáy $r$, chiều cao $h$ và đường sinh $l$. Kết luận nào sau đây sai?

A. $V={\displaystyle \frac{1}{3}}\pi r^{2}h$.

B. $S_{tp}=\pi rl+\pi r^2$.

C. $h^2=r^2+l^2$.

D. $S_{xq}=\pi rl$.

Câu 48 .  Hàm số $y=f\left(x\right)$ có giới hạn $\underset{x\to a^{-}}{lim}f\left(x\right)=+\mathrm{\infty }$ và đồ thị $\left(C\right)$ của hàm số $y=f\left(x\right)$ chỉ nhận đường thẳng $d$ làm tiệm cận đứng. Khẳng định nào sau đây đúng?

A. $d:y=a$.

B. $d:x=a$.

C. $d:x=-a$.

D. $d:y=-a$.

Câu 49 .  Rút gọn biểu thức $M={\displaystyle \frac{a^{{\displaystyle \frac{1}{5}}}\left(a^{{\displaystyle \frac{3}{10}}}-a^{-{\displaystyle \frac{1}{5}}}\right)}{a^{{\displaystyle \frac{2}{3}}}\left(a^{{\displaystyle \frac{1}{3}}}-a^{-{\displaystyle \frac{2}{3}}}\right)}}$ với $a>0,a\ne 1$, ta được kết quả là

A. ${\displaystyle \frac{1}{\sqrt{a}+1}}$.

B. ${\displaystyle \frac{1}{a+1}}$.

C. ${\displaystyle \frac{1}{a-1}}$.

D. ${\displaystyle \frac{1}{\sqrt{a}-1}}$.

Câu 50 .  Đầu mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất kép là $0,6\mathrm{\%}$ mỗi tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được số tiền cả lãi và gốc nhiều hơn 100 triệu biết lãi suất không đổi trong quá trình gửi.

A. 31 tháng.

B. 40 tháng.

C. 35 tháng.

D. 30 tháng.

Lời giải chi tiết

1. D	2. C	3. A	4. C	5. D
6. D	7. A	8. B	9. B	10. D
11. B	12. C	13. C	14. C	15. B
16. C	17. D	18. D	19. B	20. A
21. C	22. A	23. A	24. A	25. A
26. C	27. A	28. A	29. B	30. D
31. C	32. D	33. B	34. B	35. D
36. A	37. A	38. D	39. C	40. C
41. D	42. C	43. A	44. B	45. B
46. B	47. C	48. B	49. A	50. A

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 6

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 6)

Câu 1 : Cho hàm số $y={\displaystyle \frac{3x-1}{-2+x}}$. Khẳng định nào sau đây là đúng?

A. Hàm số luôn nghịch biến trên R.

B. Hàm số luôn nghịch biến trên từng khoảng xác định.                               

C. Hàm số đồng biến trên các khoảng $\left(-\mathrm{\infty };2\right)$ và $\left(2;+\mathrm{\infty }\right)$.

D. Hàm số nghịch biến trên các khoảng  $\left(-\mathrm{\infty };-2\right)$ và $\left(-2;+\mathrm{\infty }\right)$.

Câu 2 : Hàm số $y=\ln \left(x+2\right)+{\displaystyle \frac{3}{x+2}}$ đồng biến trên khoảng nào?

A. $\left(-\mathrm{\infty };1\right)$.

B. $\left(1;+\mathrm{\infty }\right)$.

C. $\left({\displaystyle \frac{1}{2}};1\right)$.

D. $\left(-{\displaystyle \frac{1}{2}};+\mathrm{\infty }\right)$.

Câu 3 : Cho hàm số $y=f\left(x\right)$ có đồ thị như hình vẽ. Trên khoảng $\left(-1;3\right)$ đồ thị hàm số $y=f\left(x\right)$ có mấy điểm cực trị?

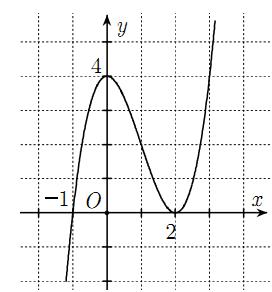
A. 2.

B. 1.                                       

C. 0.   

D. 3.

Câu 4 : Cho hàm số$y=\sqrt{x^2-3x}$. Khẳng định nào sau đây đúng?

A. Hàm số có 2 điểm cực trị. 

B. Hàm số đạt cực tiểu tại $x=0$.

C. Hàm số đạt cực đại tại $x=3$.

D. Hàm số không có cực trị.

Câu 5 : Tìm tất cả giá trị của tham số m để đồ thị hàm số $y=x^4-2m{x}^2+2m-3$ có ba điểm cực trị là ba đỉnh của tam giác vuông.

A. $m=-1$.

B. $m\ne 0$.

C. $m=2$.

D. $m=1$.

Câu 6 : Tìm phương trình đường tiệm cận đứng của đồ thị hàm số $y={\displaystyle \frac{2017x-2018}{x+1}}$.

A. $x=2017$.

B. $x=-1$.

C. $y=2017$.         

D. $y=-1$.

Câu 7 : Cho hàm số $y=f\left(x\right)$ có $\underset{x\to -\mathrm{\infty }}{lim}f\left(x\right)=-1$ và $\underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)=-1$. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y=2-2017f\left(x\right)$.

A. $y=-2017$.

B. $y=1$.

C. $y=2017$.         

D. $y=2019$.

Câu 8 : Tìm số đường tiệm cận của đồ thị hàm số $y={\displaystyle \frac{2x-\sqrt{x^2-x-6}}{x^2-1}}$.

A. 1.

B. 2.

C. 0.

D. 4.

Câu 9 : Hỏi có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y={\displaystyle \frac{x^2-3x+2}{x^2-mx-m+5}}$ không có đường tiệm cận đứng?

A. 9.

B. 10. 

C. 11. 

D. 8.

Câu 10 : Phương trình tiếp tuyến của đồ thị hàm số $y=x^3-3x^2+1$ tại điểm $A\left(3;1\right)$ là:

A. $y=-9x-26$.

B. $y=9x-26$.

C. $y=-9x-3$.

D. $y=9x-2$.

Câu 11 : Với $x\in \left(0;{\displaystyle \frac{\pi }{2}}\right)$, hàm số $y=2\sqrt{\sin x}-2\sqrt{\cos x}$ có đạo hàm là:

A. $y^{\prime }={\displaystyle \frac{1}{\sqrt{\sin x}}}-{\displaystyle \frac{1}{\sqrt{\cos x}}}$.

B. $y^{\prime }={\displaystyle \frac{1}{\sqrt{\sin x}}}+{\displaystyle \frac{1}{\sqrt{\cos x}}}$.                                              

C. $y^{\prime }={\displaystyle \frac{\cos x}{\sqrt{\sin x}}}-{\displaystyle \frac{\sin x}{\sqrt{\cos x}}}$.

D. $y^{\prime }={\displaystyle \frac{\cos x}{\sqrt{\sin x}}}+{\displaystyle \frac{\sin x}{\sqrt{\cos x}}}$.

Câu 12 : Cho hàm số $y=-2017e^{-x}-3e^{-2x}$. Mệnh đề nào dưới đây đúng?

A. $y^{″}+3y^{\prime }+2y=-2017$.

B. $y^{″}+3y^{\prime }+2y=-3$.

C. $y^{″}+3y^{\prime }+2y=0$.        

D. $y^{″}+3y^{\prime }+2y=2$.

Câu 13 : Đồ thị hình bên là đồ thị của một trong 4 hàm số dưới dây. Hỏi đó là hàm số nào?

A. $y=x^3-3x^2-3x-1$.

B. $y={\displaystyle \frac{1}{3}}{x}^3+3x-1$.    

C. $y=x^3+3x^2-3x+1$.

D. $y=x^3-3x-1$.

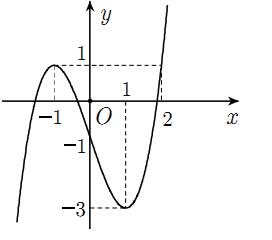
Câu 14 : Cho hàm số $y={\displaystyle \frac{x+1}{x-1}}$ có đồ thị $\left(C\right)$. Gọi $A,B$$\left(x_A>x_B>0\right)$ là hai điểm trên $\left(C\right)$ có tiếp tuyến tại $A,B$ song song với nhau và $AB=2\sqrt{5}$. Tính $x_A-x_B$.

 A. $x_A-x_B=2$.

B. $x_A-x_B=4$.

C. $x_A-x_B=2\sqrt{2}$.

D. $x_A-x_B=\sqrt{2}$.

Câu 15 : Giá trị nhỏ nhất của hàm số $y={\displaystyle \frac{\ln x}{x}}$ trên đoạn $\left[1;e\right]$ là:

A. 0.

B. 1.

C. $-{\displaystyle \frac{1}{e}}$.

D. $e$.

Câu 16 : Trong các hình chữ nhật có chu vi bằng 16, hình chữ nhật có diện tích lớn nhất bằng

A. 64.

B. 4.   

C. 16. 

D. 8.

Câu 17 : Cho hàm số $y={\displaystyle \frac{x+1}{x-1}}$ có đồ thị $\left(C\right)$. Gọi $M\left(x_M;y_M\right)$ là một điểm trên $\left(C\right)$ sao cho tổng khoảng cách từ điểm M đến hai trục tọa độ là nhỏ nhất. Tổng $x_M+y_M$ bằng

A. $2\sqrt{2}-1$.

B. 1.

C. $2-\sqrt{2}$.

D. $2-2\sqrt{2}$.

Câu 18 : Tìm số giao điểm của đồ thị $\left(C\right):y=x^3-3x^2+2x+2017$ và đường thẳng $y=2017$.

A. 3.

B. 0.   

C. 1.   

D. 2.

Câu 19 : Cho hàm số $y=m{x}^3-x^2-2x+8m$ có đồ thị $\left(C_m\right)$. Tìm tất cả các giá trị của tham số m để đồ thị $\left(C_m\right)$ cắt trục hoành tại ba điểm phân biệt.

A. $m\in \left(-{\displaystyle \frac{1}{6}};{\displaystyle \frac{1}{2}}\right)$.

B. $m\in \left[-{\displaystyle \frac{1}{6}};{\displaystyle \frac{1}{2}}\right]$.

C. $m\in \left(-{\displaystyle \frac{1}{6}};{\displaystyle \frac{1}{2}}\right)\mathrm{\setminus }\left\{0\right\}$.           

D. $m\in \left(-\mathrm{\infty };{\displaystyle \frac{1}{2}}\right)\mathrm{\setminus }\left\{0\right\}$.

Câu 20 : Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y=\left(m+1\right)x^4-2\left(2m-3\right)x^2+6m+5$ cắt trục hoành tại 4 điểm phân biệt có hoành độ $x_1,x_2,x_3,x_4$ thỏa mãn $x_1<x_2<x_3<1<x_4$.

A. $m\in \left(-1;-{\displaystyle \frac{5}{6}}\right)$.

B. $m\in \left(-3;-1\right)$.

C. $m\in \left(-3;1\right)$.      

D. $m\in \left(-4;-1\right)$.

Câu 21 : Tiếp tuyến với đồ thị hàm số $y={\displaystyle \frac{2x+1}{x+1}}$ tại điểm có hoành độ bằng 0 cắt hai trục tọa độ lần lượt tại $A$ và $B$. Diện tích tam giác OAB bằng

A. 2.

B. 3.

C. ${\displaystyle \frac{1}{2}}$.   

D. ${\displaystyle \frac{1}{4}}$.

Câu 22 : Cho hàm số $y={\displaystyle \frac{ax+b}{x+1}}$ có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau:

A. $a<b<0$.         

B. $b<0<a$.         

C. $0<b<a$.

D. $0<a<b$.

                                                                                                                                                

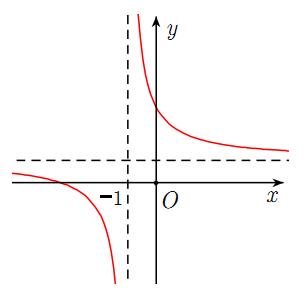
Câu 23 : Tìm tổng $S=1+2^2{\log }_{\sqrt{2}}2+3^2{\log }_{\sqrt[3]{2}}2$$+4^2{\log }_{\sqrt[4]{2}}2+...+{2017}^2{\log }_{\sqrt[2017]{2}}2$.

A. $S={1008}^2{.2017}^2$.          

B. $S={1007}^2{.2017}^2$.

C. $S={1009}^2{.2017}^2$.

D. $S={1010}^2{.2017}^2$.

Câu 24 : Cho hàm số $y=\ln x$. Khẳng định nào sau đây là sai?

A. Hàm số đồng biến trên khoảng $\left(0;+\mathrm{\infty }\right)$.

B. Hàm số có tập giá trị là $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng

D. Hàm số có tập giá trị là $\left(0;+\mathrm{\infty }\right)$.

Câu 25 : Tính đạo hàm của hàm số $y={\log }_2\left(2x+1\right)$.

A. $y^{\prime }={\displaystyle \frac{2}{2x+1}}$.

B. $y^{\prime }={\displaystyle \frac{2}{\left(2x+1\right)\ln 2}}$.

C. $y^{\prime }={\displaystyle \frac{1}{\left(2x+1\right)\ln 2}}$.  

D. $y^{\prime }={\displaystyle \frac{1}{2x+1}}$.

Câu 26 : Tìm tập xác định D của hàm số $y={\left(2-x\right)}^{1-\sqrt{3}}$.

A. $D=\left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

B. $D=\left(-\mathrm{\infty };2\right]$.

C. $D=\left(-\mathrm{\infty };2\right)$.

D. $D=\left(2;+\mathrm{\infty }\right)$.

Câu 27 : Cho $a>0$$,a\ne 1$ và $x,y$ là hai số thực khác 0. Khẳng định nào sau đây là khẳng định đúng?

A. ${\log }_a{x}^2=2{\log }_{a}x$.

B. ${\log }_a\left(xy\right)={\log }_{a}x+{\log }_{a}y$.

C. ${\log }_a\left(x+y\right)={\log }_{a}x+{\log }_{a}y$.

D. ${\log }_a\left(xy\right)={\log }_a\left|x\right|+{\log }_a\left|y\right|$.

Câu 28 : Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y={\displaystyle \frac{m{x}^3}{3}}+7m{x}^2+14x-m+2$ nghịch biến trên nửa khoảng $\left[1;+\mathrm{\infty }\right)$.

A. $\left(-\mathrm{\infty };-{\displaystyle \frac{14}{15}}\right)$.

B. $\left(-\mathrm{\infty };-{\displaystyle \frac{14}{15}}\right]$.

C. $\left[-2;-{\displaystyle \frac{14}{15}}\right]$.        

D. $\left[-{\displaystyle \frac{14}{15}};+\mathrm{\infty }\right)$.

Câu 29 : Cho đồ thị hàm số $y=a{x}^3+b{x}^2+cx+d$ có đồ thị như hình bên. Khẳng định nào sau đây là khẳng định đúng?

A. $a,b,c<0;d>0$.

B. $a,b,d>0;c<0$.        

C. $a,c,d>0;d<0$.

D. $a,d>0;b,c<0$.

Câu 30 : Số mặt phẳng đối xứng của khối lăng trụ tam giác đều là:

A. 3.

 B. 4.

C. 6.

D. 9.

Câu 31 : Hỏi khối đa diện đều loại $\left\{4;3\right\}$ có bao nhiêu mặt ?

A. 4.

B. 20.

C. 6.

D. 12.

Câu 32 : Cho hình lập phương $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ có cạnh bằng $2a\sqrt{2}$. Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$. Tính S.

A. $S=4a^2\sqrt{3}$.

B. $S=8a^2$.

C. $S=16a^2\sqrt{3}$.

D. $S=8a^2\sqrt{3}$.

Câu 33 : Khẳng định nào sau đây là khẳng định sai?

A. $\cos x=0\iff x={\displaystyle \frac{\pi }{2}}+k2\pi$.        

B. $\cos x=1\iff x=k2\pi$.

C. $\cos x=-1\iff x=\pi +k2\pi$.           

D. $\cos x=0\iff x={\displaystyle \frac{\pi }{2}}+k\pi$.

Câu 34 : Giải phương trình $\cos 2x+5\sin x-4=0$.

A. $x={\displaystyle \frac{\pi }{2}}+k\pi$.

B. $x=-{\displaystyle \frac{\pi }{2}}+k\pi$.

C. $x=k2\pi$.

D. $x={\displaystyle \frac{\pi }{2}}+k2\pi$.

Câu 35 : Gọi S là tổng các nghiệm của phương trình ${\displaystyle \frac{\sin x}{\cos x+1}}=0$ trên đoạn $\left[0;2017\pi \right]$. Tính S.

A. $S=2035153\pi$.

B. $S=1001000\pi$.

C. $S=1017072\pi$.

D. $S=200200\pi$.

Câu 36 : Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?

A. 648.           

B. 1000.

C. 729.           

D. 720.

Câu 37 : Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn có cùng màu là:

A. ${\displaystyle \frac{1}{4}}$.

B. ${\displaystyle \frac{1}{9}}$.

C. ${\displaystyle \frac{4}{9}}$.   

D. ${\displaystyle \frac{5}{9}}$.

Câu 38 : Trong khai triển đa thức $P\left(x\right)={\left(x+{\displaystyle \frac{2}{\sqrt{x}}}\right)}^6\left(x>0\right)$, hệ số của $x^3$ là:

A. 60. 

B. 80. 

C. 160

D. 240.

Câu 39 : Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, $SA\mathrm{\perp }\left(ABC\right)$ và $SA=a\sqrt{3}$. Tính góc giữa đường thẳng SB với mặt phẳng (ABC).

A. ${75}^{\circ }$.

B. ${60}^{\circ }$.

C. ${45}^{\circ }$.

D. ${30}^{\circ }$.

Câu 40 : Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh a;  $SA\mathrm{\perp }\left(ABCD\right)$ và $SA=2a$. Tính khoảng cách d  từ điểm B đến $\left(SCD\right)$.

A. $d={\displaystyle \frac{a\sqrt{5}}{5}}$.      

B. $d=a$.

C. $d={\displaystyle \frac{4a\sqrt{5}}{5}}$.

D. $d={\displaystyle \frac{2a\sqrt{5}}{5}}$.

Câu 41 : Cho hình hộp $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ có đáy là hình thoi cạnh a, $\widehat{ABC}={60}^{\circ }$ và thể tích bằng $\sqrt{3}{a}^3$. Tính chiều cao h của hình hộp đã cho.

A. $h=2a$.

B. $h=a$.

C. $h=3a$.

D. $h=4a$.

Câu 42 : Diện tích ba mặt của hình hộp lần lượt bằng $20c{m}^3,28c{m}^3,35c{m}^3$. Thể tích của hình hộp đó bằng

A. 165 $c{m}^3$.    

B. 190 $c{m}^3$.     

C. 140$c{m}^3$.

D. 160 $c{m}^3$.

Câu 43 : Cho hình chóp tứ giác $S.ABCD$ có đáy là hình vuông, mặt bên$\left(SAB\right)$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm B đến mặt phẳng (SCD) bằng ${\displaystyle \frac{3\sqrt{7}a}{7}}$. Tính thể tích V của khối chóp  $S.ABCD$.

A. $V={\displaystyle \frac{1}{3}}{a}^3$.

B. $V=a^3$.

C. $V={\displaystyle \frac{2}{3}}{a}^3$.

D. $V={\displaystyle \frac{3}{2}}{a}^3$.

Câu 44 : Cho hình chóp $S.ABC$ có SA vuông góc với đáy, $SA=2BC$ và $\widehat{BAC}={120}^{\circ }$. Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng $\left(ABC\right)$ và $\left(AMN\right)$.

A. ${45}^{\circ }$.

B. ${60}^{\circ }$.

C. ${15}^{\circ }$.

D. ${30}^{\circ }$.

Câu 45 : Cho hình lăng trụ $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có đáy $ABC$ là tam giác đều cạnh a, tam giác $A^{\prime }BC$ đều và nằm trong mặt phẳng vuông góc với mặt phẳng $\left(ABC\right)$, M là trung điểm của cạnh $C{C}^{\prime }$. Tính cosin góc $\alpha$giữa hai đường thẳng AA’ và BM.

A. $\cos \alpha ={\displaystyle \frac{2\sqrt{22}}{11}}$.

B. $\cos \alpha ={\displaystyle \frac{\sqrt{11}}{11}}$.

C. $\cos \alpha ={\displaystyle \frac{\sqrt{33}}{11}}$.

D. $\cos \alpha ={\displaystyle \frac{\sqrt{22}}{11}}$.

Câu 46 : Cho hình lăng trụ đứng $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có đáy $ABC$ là tam giác vuông tại A. Biết $AB=2a$,$AC=a,A{A}^{\prime }=4a$. Gọi M là điểm thuộc cạnh AA’ sao cho $M{A}^{\prime }=3MA$. Tính khoảng cách giữa hai đường thẳng chéo nhau $BC$ và $C^{\prime }M$.

A. ${\displaystyle \frac{6a}{7}}$.          

B. ${\displaystyle \frac{8a}{7}}$.           

C. ${\displaystyle \frac{4a}{3}}$.          

D. ${\displaystyle \frac{4a}{7}}$.

Câu 47 : Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy a và đường cao $a\sqrt{3}$.

A. $2\pi a^2$.

B. $2\pi a^2\sqrt{3}$.

C. $\pi a^2$.

D. $\pi a^2\sqrt{3}$.

Câu 48 : Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là:

A. ${\displaystyle \frac{\pi a^3\sqrt{3}}{6}}$.

B. ${\displaystyle \frac{\pi a^3\sqrt{3}}{3}}$.

C. ${\displaystyle \frac{\pi a^3\sqrt{3}}{2}}$.

D. ${\displaystyle \frac{\pi a^3\sqrt{3}}{12}}$.

Câu 49 : Cho tam giác ABC có $\hat{A}={120}^{\circ },AB=AC=a$. Quay tam giác ABC (bao gồm điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:

A. ${\displaystyle \frac{\pi a^3}{3}}$.

B. ${\displaystyle \frac{\pi a^3}{4}}$.

C. ${\displaystyle \frac{\pi a^3\sqrt{3}}{2}}$.

D. ${\displaystyle \frac{\pi a^3\sqrt{3}}{4}}$.

Câu 50 : Trong các khối trụ có cùng diện tích toàn phần bằng $\pi$, gọi  là khối trụ có thể tích lớn nhất, chiều cao của  bằng:

A. ${\displaystyle \frac{\pi }{3}}$.

B. ${\displaystyle \frac{\sqrt{6}}{3}}$.

C. ${\displaystyle \frac{\sqrt{6}}{6}}$.

D. ${\displaystyle \frac{\pi \sqrt{3}}{4}}$.

Lời giải chi tiết

1. B	11. D	21. C	31. C	41. A
2. B	12. C	22. D	32. D	42. C
3. A	13. D	23. C	33. A	43. D
4. D	14. A	24. D	34. D	44. D
5. D	15. A	25. B	35. C	45. C
6. B	16. C	26. C	36. A	46. B
7. D	17. D	27. D	37. C	47. B
8. A	18. A	28. B	38. A	48. B
9. B	19. C	29. D	39. B	49. B
10. B	20. D	30. B	40. D	50. B

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 7

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 7)

Câu 1 : Cho hình nón đỉnh $S$ có đường cao bằng 6 cm, bán kính đáy bằng 10 cm. Trên đường tròn đáy lấy hai điểm $A,B$ sao cho $AB=12$cm. Diện tích tam giác $SAB$ bằng:

A. $100c{m}^2$.

B. $48c{m}^2$.

C. $40c{m}^2$.

D. $60c{m}^2$.

Câu 2 : Cho hình chóp$S.ABCD$ có đáy $ABCD$ là hình bình hành và có thể tích bằng 1. Trên cạnh $SC$lấy điểm $E$ sao cho $SE=2EC$. Tính thể tích $V$ của khối tứ diện $SEBD$.

A. $V={\displaystyle \frac{1}{3}}$.

B. $V={\displaystyle \frac{2}{3}}$.

C. $V={\displaystyle \frac{1}{6}}$.

D. $V={\displaystyle \frac{1}{12}}$.

Câu 3 : Cho ${\log }_{2}3=a$. Hãy tính ${\log }_{4}54$ theo $a$.

A. ${\log }_{4}54={\displaystyle \frac{1}{2}}\left(1+3a\right)$.

B. ${\log }_{4}54={\displaystyle \frac{1}{2}}\left(1+6a\right)$.

C. ${\log }_{4}54={\displaystyle \frac{1}{2}}\left(1+12a\right)$.

D. ${\log }_{4}54=2\left(1+6a\right)$.

Câu 4 : Giải bất phương trình${\left(\sqrt{10}-3\right)}^x>\sqrt{10}+3$ có kết quả là:

A. $x<1$.

B. $x>1$.

C. $x<-1$.

D. $x>-1$.

Câu 5 : Đồ thị bên là của hàm số nào:

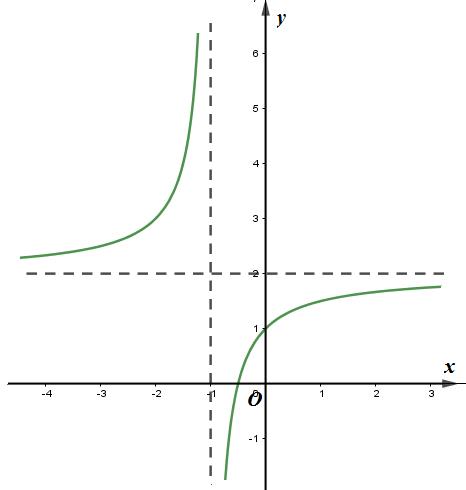
A. $y={\displaystyle \frac{2x-1}{x-1}}$.

B. $y={\displaystyle \frac{2x+5}{x+1}}$.                          

C. $y={\displaystyle \frac{x+2}{x+1}}$.    

D. $y={\displaystyle \frac{2x+1}{x+1}}$.

Câu 6 : Phương trình $3^{2x+1}-{4.3}^x+1=0$ có 2 nghiệm $x_1,x_2$ trong đó $x_1<x_2$, chọn phát biểu đúng.

A. $x_1.x_2=-1$.        

B. $2x_1+x_2=0$.

C. $x_1+2x_2=-1$.

D. $x_1+x_2=-2$.

Câu 7 : Tính đạo hàm của hàm số $y=x\ln x$.

A. $y^{\prime }=\ln x+1$.

B. $y^{\prime }=\ln x$.          

C. $y^{\prime }=\ln x-1$.

D. $y^{\prime }={\displaystyle \frac{1}{x}}$.

Câu 8 : Các điểm cực đại của hàm số $y=x-\sin 2x$là:

A. $x=\pm {\displaystyle \frac{\pi }{6}}+k\pi ,k\in Z$.

B. $x=-{\displaystyle \frac{\pi }{6}}+k\pi ,k\in Z$.

C. $x={\displaystyle \frac{\pi }{6}}+k\pi ,k\in Z$.

D. $x=\pm {\displaystyle \frac{\pi }{3}}+k2\pi ,k\in Z$.

Câu 9 : Cho khối chóp $S.ABC$ có $SA\mathrm{\perp }\left(ABC\right)$; tam giác $ABC$ vuông tại $A$, biết $BC=3a$; $AB=a$. Góc giữa mặt phẳng $\left(SBC\right)$ và $\left(ABC\right)$ bằng ${45}^0$. Tính thể tích khối chóp $S.ABC$ theo $a$.

A. $V_{S.ABC}={\displaystyle \frac{4a^3}{9}}$.

B. $V_{S.ABC}={\displaystyle \frac{a^3\sqrt{2}}{6}}$.

C. $V_{S.ABC}={\displaystyle \frac{a^3\sqrt{2}}{2}}$.

D. $V_{S.ABC}={\displaystyle \frac{2a^3}{9}}$.

Câu 10 : Khối nón có chiều cao $h=3cm$ và bán kính đáy $r=2cm$ thì có thể tích bằng:

A. $16\pi \left(c{m}^2\right)$.    

B. $4\pi \left(c{m}^2\right)$.      

C. ${\displaystyle \frac{4}{3}}\pi \left(c{m}^2\right)$.

D. $4\pi \left(c{m}^2\right)$.

Câu 11 : Giá trị nhỏ nhất của số thực $m$ để hàm số $y={\displaystyle \frac{1}{3}}{x}^3+m{x}^2-mx-m$ đồng biến trên $\mathbb{R}$ là:

A. $m=-2$.

B. $m=1$.

C. $m=-1$.

D. $m=0$.

Câu 12 : Giải phương trình ${\log }_6{x}^2=2$ được kết quả là:

A. $x\in \left\{\pm 36\right\}$.  

B. $x\in \left\{\pm 6\right\}$.    

C. $x\in \left\{\pm \sqrt{6}\right\}$.

D. $x=6$.

Câu 13 : Cho lăng trụ tứ giác đều $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$có đáy là hình vuông cạnh a, $A{A}^{\prime }=3a$. Thể tích khối lăng trụ đã cho là:

A. $12a^3$.

B. $a^3$.    

C. $6a^3$.

D. $3a^3$.

Câu 14 : Khối chóp ngũ giác có số cạnh là:

A. 20. 

B. 15. 

C. 5.   

D. 10.

Câu 15 : Tìm các giá trị thực của tham số m sao cho phương trình $x^3-3x+4m-1=0$ có ít nhất một nghiệm thực trong đoạn $\left[-3;4\right]$?

A. ${\displaystyle \frac{-51}{4}}\le m\le {\displaystyle \frac{19}{4}}$.

B. ${\displaystyle \frac{-51}{4}}<m<{\displaystyle \frac{19}{4}}$.

C. $-51<m<19$.

D. $-51\le m\le 19$.

Câu 16 : Giá trị lớn nhất của hàm số $f\left(x\right)={\displaystyle \frac{mx-1}{2x+m}}$ trên đoạn $\left[3;5\right]$ bằng 2 khi và chỉ khi:

A. $m=7$.

B. $m=\left\{7;13\right\}$.

C. $m\in \mathrm{\varnothing }$.

D. $m=13$.

Câu 17 : Cho hình chóp $S.ABC$ có $SA=a,SB=b,SC=c$ và $\widehat{ASB}=\widehat{BSC}=\widehat{CSA}={60}^0$. Tính thể tích của khối chóp $S.ABC$.

A. ${\displaystyle \frac{\sqrt{2}}{12abc}}$.

B. ${\displaystyle \frac{\sqrt{2}}{12}}abc$.

C. ${\displaystyle \frac{\sqrt{2}}{4}}abc$.

D. ${\displaystyle \frac{\sqrt{2}}{4abc}}$.

Câu 18 : Giá trị nhỏ nhất của hàm số $y=x\sqrt{1-x^2}$là:

A. 2.   

B. 1.   

C. -1.  

D. ${\displaystyle \frac{-1}{2}}$.

Câu 19 : Gọi $M$ và $m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=2{\sin }^{2}x-\cos x+1$. Thể thì $M.m$ bằng:

A. ${\displaystyle \frac{25}{4}}$.           

B. ${\displaystyle \frac{25}{8}}$.

C. 2.   

D. 0.

Câu 20 : Khối đa diện đều loại $\left\{4;3\right\}$ có số đỉnh, số cạnh và số mặt lần lượt bằng:

A. 6, 12, 8.

B. 8, 12, 6.

C. 12, 30, 20

D. 4, 6, 4.

Câu 21: Cho bất phương trình ${\log }_{{\displaystyle \frac{1}{5}}}f\left(x\right)>{\log }_{{\displaystyle \frac{1}{5}}}g\left(x\right)$. Khi đó, bất phương trình tương đương:

A. $f\left(x\right)<g\left(x\right)$.

B. $g\left(x\right)>f\left(x\right)\ge 0$.

C. $g\left(x\right)>f\left(x\right)>0$.  

D. $f\left(x\right)>g\left(x\right)$.

Câu 22 : Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh a, $SA\mathrm{\perp }\left(ABCD\right)$ và $SA=a\sqrt{3}$. Thể tích của khối chóp $S.ABCD$ là:

A. ${\displaystyle \frac{a^3\sqrt{3}}{3}}$.

B. ${\displaystyle \frac{a^3\sqrt{3}}{6}}$.

C. ${\displaystyle \frac{a^3\sqrt{2}}{3}}$.

D. ${\displaystyle \frac{a^3\sqrt{2}}{6}}$.

Câu 23 : Cho các số thực $x,y$ và a thỏa mãn $x>y;a>1$. Khi đó:

A. $a^x<a^y$.

B. $a^x\le a^y$.

C. $a^x>a^y$.

D. $a^x\ge a^y$.

Câu 24 : Ông An gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất 7%/năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Sau thời gian 10 năm nếu không rút lần nào thì số tiền mà ông An nhận được tính cả gốc lẫn lãi là (đơn vị đồng):

A. ${10}^8{\left(1+0,0007\right)}^{10}$.

B. ${10}^8{\left(1+0,07\right)}^{10}$.

C. ${10}^8.0,{07}^{10}$.     

D. ${10}^8{\left(1+0,7\right)}^{10}$.

Câu 25 : Cho hàm số $y=x^3-3x^2+2$, hãy chọn khẳng định đúng:

A. Hàm số có đúng ba điểm cực trị.  

B. Hàm số có đúng hai điểm cực trị.  

C. Hàm số chỉ có một điểm cực trị.   

D. Hàm số không có điểm cực trị.

Câu 26 : Giải bất phương trình ${\log }_{{\displaystyle \frac{1}{5}}}\left(5x-3\right)>-2$, có có nghiệm là:

A. $x>{\displaystyle \frac{28}{5}}$.

B. ${\displaystyle \frac{3}{5}}<x<{\displaystyle \frac{28}{5}}$.

C. ${\displaystyle \frac{3}{5}}\le x<{\displaystyle \frac{28}{5}}$.

D. $x<{\displaystyle \frac{28}{5}}$.

Câu 27 : Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng a, góc tạo bởi mặt bên và mặt đáy là $\alpha$. Thể tích khối chóp $S.ABCD$là:

A. ${\displaystyle \frac{a^3\tan \alpha }{2}}$.           

B. ${\displaystyle \frac{a^3\tan \alpha }{3}}$.           

C. ${\displaystyle \frac{a^3\tan \alpha }{6}}$.           

D. ${\displaystyle \frac{2a^3\tan \alpha }{3}}$.

Câu 28 : Giả sử $A$ và $B$là các giao điểm của đường cong $y=x^3-3x+2$ và trục hoành. Tính độ dài đoạn thẳng $AB$:

A. $AB=6\sqrt{5}$. 

B. $AB=4\sqrt{2}$.

C. $AB=3$.

D. $AB=5\sqrt{3}$.

Câu 29 : Cho hàm số $y=x^3-2m{x}^2+1$ có đồ thị $\left(C_m\right)$. Tìm m sao cho $\left(C_m\right)$ cắt đường thẳng $d:y=x+1$ tại ba điểm phân biệt có hoành độ $x_1,x_2,x_3$ thỏa mãn $x_1+x_2+x_3=101$

A. $m={\displaystyle \frac{101}{2}}$.

B. $m=50$.

C. $m=51$.

D. $m=49$.

Câu 30 : Số tiệm cận của đồ thị hàm số $y={\displaystyle \frac{x^2-6x+3}{x^2-3x+2}}$ là:

A. 6.

B. 2.

C. 1.

D. 3.

Câu 31 : Đồ thị bên là của hàm số nào?

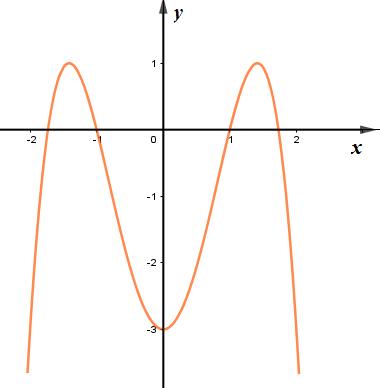
A. $y=-x^4+4x^2-3$.         

B. $y=x^4-3x^2-3$.  

C. $y=x^4+2x^2-3$.

D. $y=-{\displaystyle \frac{1}{4}}{x}^4+3x^2-3$.

Câu 32 : Cho hàm số $y=a{x}^3+b{x}^2+cx+d$ có đồ thị trong hình bên. Hỏi phương trình  $a{x}^3+b{x}^2+cx+d+2=0$ có bao nhiêu nghiệm?

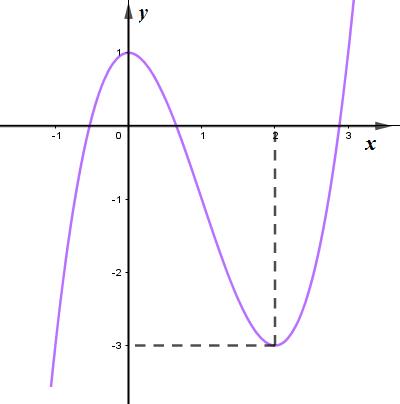
A. Phương trình có đúng một nghiệm.                                              

B. Phương trình có đúng hai nghiệm.                                    

C. Phương trình không có nghiệm.

D. Phương trình có đúng ba nghiệm

Câu 33 : Phương trình ${\log }^{2}x-\log x-2=0$ có bao nhiêu nghiệm?

A. 1.

B. 2.

C. 3.

D. 0.

Câu 34 : Cho lăng trụ tam giác đều tất cả các cạnh bằng a. Một hình trụ tròn xoay có hai đáy là hai hình tròn ngoại tiếp hai đáy của lăng trụ. Thể tích của khối trụ tròn xoay bằng:

A. ${\displaystyle \frac{\pi a^3}{9}}$.

B. $\pi a^3$.

C. $3\pi a^3$.

D. ${\displaystyle \frac{\pi a^3}{3}}$.

Câu 35 : Cho hình trụ (T) có độ dài đường sinh $l$, bán kính đáy $r$. Kí hiệu $S_{xq}$ là diện tích xung quanh của (T). Công thức nào sau đây đúng?

A. $S_{xq}=3\pi rl$.

B. $S_{xq}=2\pi rl$.        

C. $S_{xq}=\pi rl$.          

D. $S_{xq}=2\pi r^{2}l$.

Câu 36 : Điều kiện cần và đủ của tham số m để hàm số $y=x^3-x^2+mx-5$ có cực trị là:

A. $m>{\displaystyle \frac{1}{3}}$.

B. $m<{\displaystyle \frac{1}{3}}$.

C. $m\le {\displaystyle \frac{1}{3}}$.

D. $m\ge {\displaystyle \frac{1}{3}}$.

Câu 37 : Tập xác định của hàm số $y={\log }_2{\displaystyle \frac{x+3}{2-x}}$ là:

A.$\left[-3;2\right)$.

B. $\left(-\mathrm{\infty };-3\right)\cup \left(2;+\mathrm{\infty }\right)$.

C. $R\mathrm{\setminus }\left\{2\right\}$.

D. $\left(-3;2\right)$.

Câu 38 : Cho hình chóp $S.ABC$ có tam giác $ABC$ đều cạnh $a=3cm$, $SA\mathrm{\perp }\left(ABC\right)$ và $SA=2a$. Tính thể tích khối cầu ngoại tiếp hình chóp $S.ABC$.

A. ${\displaystyle \frac{8a^3\pi }{3\sqrt{3}}}c{m}^3$.

B. ${\displaystyle \frac{4a^3\pi }{3}}c{m}^3$.

C. $32\pi \sqrt{3}c{m}^3$.   

D. $16\pi \sqrt{3}c{m}^3$.

Câu 39 : Cho hình lăng trụ đứng $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có thể tích bằng $V$. Các điểm $M,N,P$ lần lượt thuộc cạnh $A{A}^{\prime },B{B}^{\prime },C{C}^{\prime }$ sao cho ${\displaystyle \frac{AM}{A{A}^{\prime }}}={\displaystyle \frac{1}{2}},{\displaystyle \frac{BN}{B{B}^{\prime }}}={\displaystyle \frac{CP}{C{C}^{\prime }}}={\displaystyle \frac{3}{4}}$. Thể tích khối đa diện $ABC.MNP$ là:

A. ${\displaystyle \frac{2}{3}}V$.

B. ${\displaystyle \frac{1}{8}}V$.

C. ${\displaystyle \frac{1}{3}}V$.

D. ${\displaystyle \frac{1}{2}}V$.

Câu 40 : Tìm nghiệm của phương trình ${\log }_x\left(4-3x\right)=2$.

A. $x=1$.

B. $x=4$.

C. $x\in \mathrm{\varnothing }$.

D. $x\in \left\{1;-4\right\}$.

Câu 41 : Với giá trị nào của số thực m thì hàm số $y={\displaystyle \frac{x+m}{x+1}}$ đồng biến trên từng khoảng xác định?

A. $m<1$.

B. $m\ge 1$.

C. $m>1$.

D. $m\le 1$.

Câu 42 : Khối cầu có bán kính 3cm thì có thể tích là:

A. $9\pi \left(c{m}^3\right)$.

B. $12\pi \left(c{m}^3\right)$.  

C. $36\pi \left(c{m}^3\right)$.  

D. $27\pi \left(c{m}^3\right)$.

Câu 43 : Nghiệm của phương trình $5^{2-x}=125$ là:

A. $x=-1$.

B. $x=-5$.

C. $x=3$.

D. $x=1$.

Câu 44 : Cho hình chóp $S.ABC$ có đáy $ABC$là tam giác vuông tại $A$, $\widehat{ABC}={30}^0$. Tam giác $SBC$ là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là:

A. ${\displaystyle \frac{a^3}{16}}$. 

B. ${\displaystyle \frac{3\sqrt{3}{a}^3}{16}}$.

C. ${\displaystyle \frac{3a^3}{16}}$.

D. ${\displaystyle \frac{\sqrt{3}{a}^3}{16}}$.

Câu 45 : Gọi$y_1,y_2$ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số $y=-x^4+10x^2-9$. Khi đó, $\left|y_1-y_2\right|$ bằng:

A. 7.

B. $2\sqrt{5}$.

C. 25.

D. 9.

Câu 46 : Giá trị nhỏ nhất của hàm số $y=e^{2x}+3e^x-1$ trên đoạn $\left[\ln 2;\ln 5\right]$ là:

A. $e^2$.    

B. 9.

C. $e^9$.    

D. 39.

Câu 47 : ${\log }_{{\displaystyle \frac{1}{a}}}\sqrt[3]{a^7},\left(a>0,a\ne 1\right)$ bằng:

A. $-{\displaystyle \frac{3}{7}}$.

B. ${\displaystyle \frac{7}{3}}$.     

C. ${\displaystyle \frac{3}{7}}$.    

D. $-{\displaystyle \frac{7}{3}}$.

Câu 48 : Tiệm cận đứng của đồ thị hàm số $y={\displaystyle \frac{2x-3}{x-7}}$có phương trình là:

A. $y=7$.

B. $y=2$.

C. $x=7$.

D. $x=2$.    

Câu 49 : Cho hàm số $y={\displaystyle \frac{3x+1}{x-1}}$. Chọn khẳng định đúng:

A. Hàm số nghịch biến trên $\left(-\mathrm{\infty };1\right)\cup \left(1;+\mathrm{\infty }\right)$.

B. Hàm số nghịch biến trên từng khoảng xác định của nó.               

C. Hàm số đồng biến trên R.

D. Hàm số nghịch biến trên R.

Câu 50 : Tập xác định của hàm số $y={\left(2x-1\right)}^{-{\displaystyle \frac{1}{2}}}$ là:

A. $\left[{\displaystyle \frac{1}{2}};+\mathrm{\infty }\right)$.

B. $R\mathrm{\setminus }\left\{{\displaystyle \frac{1}{2}}\right\}$.

C. $\left({\displaystyle \frac{1}{2}};+\mathrm{\infty }\right)$.  

D. $R$.

Lời giải chi tiết

1. D	11. C	21. C	31. A	41. A
2. A	12. B	22. A	32. D	42. C
3. A	13. D	23. C	33. B	43. A
4. C	14. D	24. B	34. D	44. A
5. D	15. A	25. B	35. B	45. C
6. A	16. A	26. B	36. B	46. B
7. A	17. B	27. C	37. D	47. D
8. B	18. D	28. C	38. C	48. C
9. A	19. D	29. A	39. A	49. B
10. B	20. A	30. D	40. C	50. C

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 8

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 8)

Câu 1 : Cho hàm số $y={\displaystyle \frac{2x-1}{x-2}}$. Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng $\left(2;+\mathrm{\infty }\right)$.

B. Hàm số nghịch biến trên khoảng $\left({\displaystyle \frac{1}{2}};+\mathrm{\infty }\right)$.

C. Hàm số nghịch biến trên khoảng $\left(2;+\mathrm{\infty }\right)$.   

D. Hàm số đồng biến trên khoảng $\left({\displaystyle \frac{1}{2}};+\mathrm{\infty }\right)$.

Câu 2 : Cho lăng trụ tứ giác đều có cạnh bằng a và cạnh bên bằng 2a. Diện tích xung quanh của hình lăng trụ đã cho bằng

A. $10a^2$.

B. $9a^2$.

C. $8a^2$.

D. $4a^2$.

Câu 3 : Thể tích của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh $2\sqrt{2}$ bằng

A. $8\pi \sqrt{6}$.

B. ${\displaystyle \frac{256\pi }{3}}$.

C. ${\displaystyle \frac{32\pi }{3}}$.

D. ${\displaystyle \frac{64\pi \sqrt{2}}{3}}$.

Câu 4 : Đồ thị hàm số $y={\displaystyle \frac{2x+1}{4-x^2}}$ có bao nhiêu tiệm cận?

A. 3.

B. 1.

C. 2.   

D. 4.

Câu 5 : Cho $P=\sqrt[3]{a}.a^{{\displaystyle \frac{1}{3}}},a>0$. Khẳng định nào sau đây đúng?

A. $P=a^{{\displaystyle \frac{2}{3}}}$.

B. $P=a^{{\displaystyle \frac{1}{9}}}$.

C. $P=a^{{\displaystyle \frac{11}{3}}}$.

D. $P=a^2$.

Câu 6 : Số giao điểm của đồ thị hàm số $y=x^3-4x+1$ và đường thẳng $y=x+1$ bằng

A. 1.

B. 2.

C. 3.

D. 4.

Câu 7 : Bất phương trình ${\left({\displaystyle \frac{e}{2}}\right)}^{x-1}\le {\left({\displaystyle \frac{e}{2}}\right)}^{2x+3}$ có nghiệm là

A. $x>-4$.

B. $x<-4$.

C. $x\le -4$.

D. $x\ge -4$.

Câu 8 : Cho hàm số $y=f(x)$ có đồ thị như hình vẽ

Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng $\left(-1;+\mathrm{\infty }\right)$.

B. Hàm số đồng biến trên khoảng $\left(1;+\mathrm{\infty }\right)$.

C. Hàm số đồng biến trên khoảng $\left(-1;+\mathrm{\infty }\right)$.

D. Hàm số nghịch biến trên khoảng $\left(-1;0\right)$.

Câu 9 : Tập nghiệm S của bất phương trình ${\log }_{{\displaystyle \frac{1}{2}}}\left(3x-2\right)>{\log }_{{\displaystyle \frac{1}{2}}}\left(4-x\right)$ là

A. $S=\left({\displaystyle \frac{3}{2}};4\right)$.      

B. $S=\left(-\mathrm{\infty };{\displaystyle \frac{3}{2}}\right)$.

C. $S=\left({\displaystyle \frac{2}{3}};3\right)$.      

D. $S=\left({\displaystyle \frac{2}{3}};{\displaystyle \frac{3}{2}}\right)$.

Câu 10 : Cho biểu thức $A={\log }_{\sqrt{a}}{a}^2+{\log }_{{\displaystyle \frac{1}{2}}}{4}^a,a>0,a\ne 1$. Khẳng định nào sau đây đúng?

A.$A=4+2a$.        

B. $A=4-2a$.         

C. $A=1+2a$.       

D. $A=1-2a$.

Câu 11 : Số giao điểm của đồ thị hàm số $y=\left|x-1\right|\left({\displaystyle \frac{1}{3}}{x}^2-2\left|x\right|+3\right)$ với trục hoành là

A. 3.

B. 4.

C. 1.

D. 5.

Câu 12 : Một hình đa diện có ít nhất bao nhiêu đỉnh?

A. 6.

B. 3.

C. 5.

D. 4.

Câu 13 : Tính đạo hàm của hàm số $y=x^e+e^x$.

A. $y^{\prime }=x^e.\ln x+e^x$.

B. $y^{\prime }=e.\left(e^{x-1}+x^{e-1}\right)$.         

C. $y^{\prime }=x.\left(x^{e-1}+e^{x-1}\right)$.         

D. $y^{\prime }=e.\ln x+x$.

Câu 14 : Hàm số $y=x^3-3x$ có giá trị cực đại bằng

A. 2.

B. -2.

C. 1.

D. -1.

Câu 15 : Cho hàm số $y={\displaystyle \frac{x^2-3x+3}{x-1}}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\left[-1;{\displaystyle \frac{1}{2}}\right]$. Tính tích M.m.

A. $-{\displaystyle \frac{1}{2}}$.

B. $-3$.        

C. ${\displaystyle \frac{21}{2}}$.         

D. 0.

Câu 16 : Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng

A. $2\pi a^2$.

B. ${\displaystyle \frac{3\pi a^2}{2}}$.

C. $\pi a^2$.

D. ${\displaystyle \frac{\pi a^2}{2}}$.

Câu 17 : Cho khối chóp S.ABC có ba cạnh SA, SB, SC cùng độ dài bằng a và vuông góc với nhau từng đôi một. Thể tích của khối chóp S.ABC bằng

A. ${\displaystyle \frac{a^3}{6}}$.   

B. $a^3$.   

C. ${\displaystyle \frac{a^3}{2}}$.   

D. ${\displaystyle \frac{a^3}{3}}$.

Câu 18 : Cho hàm số $y=f(x)$ liên tục trên R và có bảng biến thiên như hình vẽ

Khẳng định nào sau đây đúng?

A. Hàm số $y=f(x)$ nghịch biến trên một đoạn có độ dài bằng 1.

B. Giá trị lớn nhất của hàm số $y=f(x)$ trên R bằng 0.                             

C. Hàm số $y=f(x)$ chỉ có một cực trị.                                          

D. Giá trị nhỏ nhất của hàm số $y=f(x)$ trên R bằng -1.

Câu 19 : Thể tích của khối bát diện đều cạnh a bằng

A. ${\displaystyle \frac{a^3\sqrt{2}}{6}}$.

B. ${\displaystyle \frac{2a^3\sqrt{2}}{3}}$.

C. $2a^3\sqrt{2}$.

D. ${\displaystyle \frac{a^3\sqrt{2}}{3}}$.

Câu 20 : Trong không gian, cho hai điểm phân biệt A, B cố định. Xét điểm M di động luôn nhìn đoạn AB dưới một góc vuông. Hỏi điểm M thuộc mặt nào trong các mặt sau?

A. Mặt trụ.

B. Mặt nón.

C. Mặt cầu.

D. Mặt phẳng.

Câu 21 : Cho phương trình ${\log }_5\left(x^2+x+1\right)=1$. Khẳng định nào sau đây đúng?

A. Phương trình có một nghiệm bằng 0 và một nghiệm âm.                                     

B. Phương trình vô nghiệm.                                      

C. Phương trình có hai nghiệm âm.

D. Phương trình có hai nghiệm trái dấu.

Câu 22 : Phương trình ${\left(x^4\right)}^{{\displaystyle \frac{1}{\sqrt{2}}}}=4^{\sqrt{2}}$ có bao nhiêu nghiệm thực?

A. 1.

B. 3.

C. 2.

D. vô số.

Câu 23 : Hàm số $y=\sqrt{x^2-x}$ nghịch biến trên khoảng

A. $\left(-\mathrm{\infty };0\right)$.

B. $\left(1;+\mathrm{\infty }\right)$.

C. $\left(-\mathrm{\infty };{\displaystyle \frac{1}{2}}\right)$.

D. $\left(0;1\right)$.

Câu 24 : Cho hàm số $y={\log }_{2}x$. Xét các phát biểu

(1) Hàm số $y={\log }_{2}x$ đồng biến trên khoảng $\left(0;+\mathrm{\infty }\right)$.

(2) Hàm số $y={\log }_{2}x$ có một điểm cực tiểu.

(3) Đồ thị hàm số $y={\log }_{2}x$ có tiệm cận.

Số phát biểu đúng là

A. 0.

B. 1.

C. 3.

D. 2.

Câu 25 : Cho hàm số $y=f(x)$ có đồ thị như hình vẽ. Hàm số $y=f(x)$ là

A. $y={\displaystyle \frac{3x-1}{x+2}}$.           

B. $y=x^3-3x^2$.

C. $y=-x^3+3x^2$.

D. $y=x^4-4x^2+4$.

Câu 26 : Các tiệm cận của đồ thị hàm số $y={\displaystyle \frac{2x+1}{x-1}}$ là

A. $x=1,y=-1$.

B. $x=2,y=1$.

C. $x=-{\displaystyle \frac{1}{2}},y=1$.

D. $x=1,y=2$.

Câu 27 : Cắt một khối nón bởi mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có diện tích bằng 8. Khẳng định nào sau đây sai ?

A. Khối nón có diện tích đáy bằng $8\pi$.

B. Khối nón có diện tích xung quanh bằng $16\pi \sqrt{2}$. 

C. Khối nón có độ dài đường sinh bằng 4.

D. Khối nón có thể tích bằng ${\displaystyle \frac{16\pi \sqrt{2}}{3}}$.

Câu 28 : Tổng tất cả các nghiệm của phương trình $4^x-{3.2}^{x+1}+8=0$ bằng 

A. $1+{\log }_{2}3$. 

B. $1-{\log }_{2}3$.

C. $3$.           

D. $6$.

Câu 29 : Hàm số nào sau đây có giá trị nhỏ nhất trên đoạn $\left[0;2\right]$ bằng -2?

A. $y=x^3-10$.

B. $y=\sqrt{x+2}-2$.

C. $y={\displaystyle \frac{x-2}{x+1}}$. 

D. $y=2^x-2$.

Câu 30 : Khối mười hai mặt đều là khối đa diện đều loại

A. $\left\{3;4\right\}$.

B. $\left\{4;3\right\}$.

C. $\left\{5;3\right\}$.

D. $\left\{3;5\right\}$.

Câu 31 : Cho mặt nón có chiều cao $h=6$, bán kính đáy $r=3$. Hình lập phương $ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng

A. $3\sqrt{3}$.

B. ${\displaystyle \frac{3\sqrt{6}}{2}}$.

C. $6\sqrt{3}\left(\sqrt{2}-1\right)$.

D. $6\left(\sqrt{2}-1\right)$.

Câu 32 : Bạn Nam làm một cái máng thoát nước mưa, mặt cắt là hình thang cân có độ dài hai cạnh bên và cạnh đáy đều bằng 20cm, thành máng nghiêng với mặt đất một góc $\phi$$\left(0^0<\phi <{90}^0\right)$. Bạn Nam phải nghiêng thành máng một góc trong khoảng nào sau đây để lượng mưa thoát được là nhiều nhất?

A. $\left[{70}^0;{90}^0\right)$.

B. $\left[{10}^0;{30}^0\right)$.    

C. $\left[{30}^0;{50}^0\right)$

D. $\left[{50}^0;{70}^0\right)$.

Câu 33 : Theo thống kê dân số năm 2017, mật độ dân số của Việt Nam là 308 người$/k{m}^2$ và mức tăng trưởng dân số là $1,03\mathrm{\%}/$năm. Với mức tăng trưởng như vậy, tới năm bao nhiêu mật độ dân số Việt Nam đạt 340 người $/k{m}^2$?

A. Năm 2028.

B. Năm 2027. 

C. Năm 2026.

D. Năm 2025.

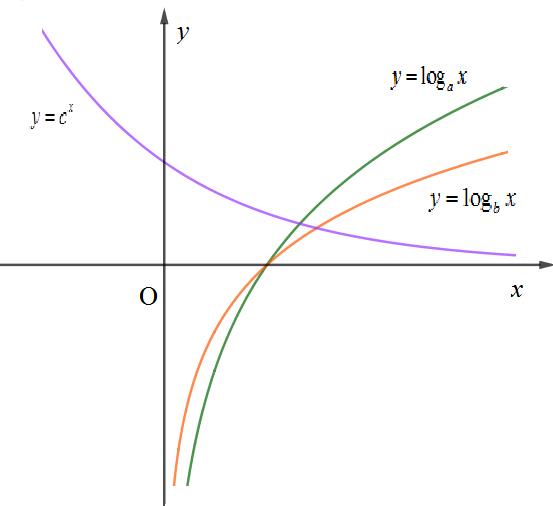
Câu 34 : Cho các hàm số $y={\log }_{a}x,y={\log }_{b}x$ và $y=c^x$ (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ

Khẳng định nào sau đây đúng?

A. $c>b>a$.

B. $c>a>b$.           

C. $a>b>c$.

D. $b>a>c$.

                                                                                                           

Câu 35 : Biết rằng phương trình $5^{2x+\sqrt{1-2x}}-m{.5}^{1-\sqrt{1-2x}}={4.5}^x$ có nghiệm khi và chỉ khi $m\in \left[a;b\right]$, với m là tham số. Giá trị của $b-a$ bằng

A. ${\displaystyle \frac{9}{5}}$.

B. 9

C. ${\displaystyle \frac{1}{5}}$.

D. 1.

Câu 36 : Cho phương trình ${\log }_4\left(x^2-4x+4\right)+{\log }_{16}{\left(x+4\right)}^4-m=0$. Tìm tất cả các giá trị của tham số thực m để phương trình đã cho có 4 nghiệm phân biệt.

A. $m<2{\log }_{2}3$.

B. $m>-2{\log }_{2}3$.                                           

C. $m\in \mathrm{\varnothing }$ .

D. $-2{\log }_{2}3<m<2{\log }_{2}3$.

Câu 37 : Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, $AB=BC=2$, $AD=4$; mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng 

A. 6.

B. 18. 

C. 2.

D. 1.

Câu 38 : Cho tứ diện ABCD có $AB=x$ thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.

A. ${\displaystyle \frac{a\sqrt{3}}{3}}$.

B. ${\displaystyle \frac{a\sqrt{6}}{4}}$.

C. ${\displaystyle \frac{a\sqrt{3}}{4}}$.

D. ${\displaystyle \frac{a\sqrt{6}}{3}}$.

Câu 39 : Cho hình chóp tam giác đều S.ABC với $SA=\sqrt{6}$, $AB=3$. Diện tích của mặt cầu có tâm A và tiếp xúc với mặt phẳng (SBC) bằng

A. ${\displaystyle \frac{54\pi }{5}}$.

B. ${\displaystyle \frac{108\pi }{5}}$.

C. $60\pi$.

D. $18\pi$.

Câu 40 : Đồ thị của hàm số nào sau đây có ba tiệm cận?

A. $y={\displaystyle \frac{\sqrt{x}}{x^2-2x}}$.

B. $y={\displaystyle \frac{x}{\sqrt{1-x^2}}}$.

C. $y={\displaystyle \frac{1}{\sqrt{x}}}$.

D. $y={\displaystyle \frac{x}{x^2-2x}}$.

Câu 41 : Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là 30cm, 20cm và 30cm (như hình vẽ)

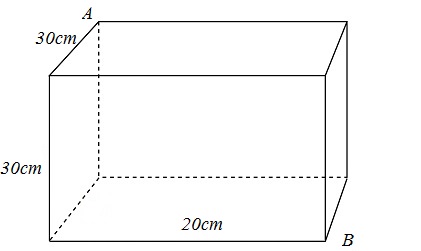
Một con kiến xuất phát từ điểm A muốn tới điểm B thì quãng đường ngắn nhất nó phải đi là bao nhiêu cm?

A. $30+10\sqrt{14}cm$.

B. $10\sqrt{34}cm$.           

C. $10\sqrt{22}cm$.

D. $20+30\sqrt{2}cm$.

Câu 42 : Cho hàm số $y={\displaystyle \frac{x^4+3}{x}}$ có giá trị cực đại $y_1$ và giá trị cực tiểu $y_2$. Giá trị của $S=y_1-y_2$ bằng

A. $S=8$.

B. $S=0$.

C. $S=-2$.

D. $S=-8$.

Câu 43 : Cho hàm số $y=f(x)$ và $y=g(x)$có đồ thị lần lượt như hình vẽ   

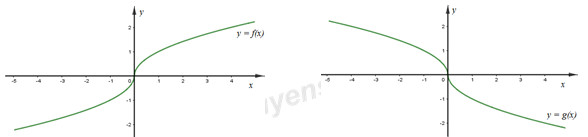
Đồ thị hàm số $y=f(x).g(x)$ là đồ thị nào dưới đây?

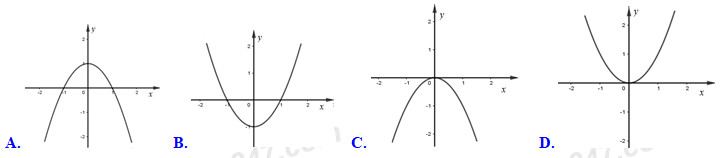
Câu 44 : Phương trình $e^x-e^{\sqrt{2x+1}}=1-x^2+2\sqrt{2x+1}$ có nghiệm trong khoảng nào sau đây?

A. $\left({\displaystyle \frac{1}{2}};1\right)$.

B. $\left(2;{\displaystyle \frac{5}{2}}\right)$.

C. $\left(1;{\displaystyle \frac{3}{2}}\right)$.

D. $\left({\displaystyle \frac{3}{2}};2\right)$.

Câu 45 : Tìm tất cả các giá trị thực của tham số m để hàm số $y=x^3-3x+m$ có giá trị cực đại và giá trị cực tiểu trái dấu.

A. $m\in \left\{-2;2\right\}$.

B. $m<-2$ hoặc $m>2$.

C. $-2<m<2$.

D. $m\in \mathbb{R}$.

Câu 46 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, $SA\mathrm{\perp }\left(ABCD\right)$ và $SA=a$. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp $S.BCE$ bằng

A. $14\pi a^2$.

B. $11\pi a^2$.

C. $8\pi a^2$.

D. $12\pi a^2$.

Câu 47 : Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y=x.\ln x$ trên đoạn $\left[{\displaystyle \frac{1}{e^2}};e\right]$ lần lượt là m và M. Tích M.m bằng

A. -1

B. 2e.

C. ${\displaystyle \frac{-2}{e}}$.

D. 1.

Câu 48 : Phương trình ${3.9}^x-{7.6}^x+{2.4}^x=0$ có hai nghiệm $x_1,x_2$. Tổng  $x_1+x_2$ bằng

A. 1.

B. ${\log }_{{\displaystyle \frac{3}{2}}}{\displaystyle \frac{7}{3}}$.

C. ${\displaystyle \frac{7}{3}}$.   

D. -1.

Câu 49 : Phương trình ${\left|x\right|}^3-3x^2-m^2=0$ (với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt ?

A. 4 nghiệm.

B. 3 nghiệm.

C. 2 nghiệm.

D. 6 nghiệm.

Câu 50 : Cho hàm số $y={\displaystyle \frac{2x+3}{x-2}}$ có đồ thị $\left(C\right)$. Có bao nhiêu giá trị thực của tham số m để đường thẳng $y=2x+m$ cắt đồ thị $\left(C\right)$ tại hai điểm phân biệt mà tiếp tuyến của $\left(C\right)$ tại hai điểm đó song song với nhau?

A. 0.

B. 2.

C. Vô số.

D. 1.

Lời giải chi tiết

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 9

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 9)

Câu 1 . Tìm tọa độ điểm M của đồ thị hàm số $y=x^3+3x-4$ và đường thẳng $y=2x-4$

A. $M\left(0;-4\right)$

B. $M\left(-3;0\right)$

C. $M\left(-1;-6\right)$

D. $M\left(1;0\right)$

Câu 2 . Tìm số nghiệm thực của phương trình ${\log }_2\left(x+1\right)+{\log }_2\left(x-1\right)=0$

A. 2

B. 0

C. 1

D. 3

Câu 3 . Tìm các giá trị của tham số m để hàm số $f\left(x\right)=\left(m^2-3\right)x-2m\ln x$ đạt cực tiểu tại điểm $x_0=1$

A. $m=-3;m=1$

B. $m=3,m=-1$

C. $m=3$

D. $m=-1$

Câu 4 . Gọi a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $f\left(x\right)=x.e^{2x}$ trên đoạn $\left[-1;1\right]$. Tính tích ab

A. $-1$

B.  $-{\displaystyle \frac{1}{2}}e$

C. ${\displaystyle \frac{1}{2}}e$

D. $1$

Câu 5 . Tìm nghiệm $x_0$ của phương trình $3^{2x+1}=21$ ?

A. $x_0={\log }_{9}21$

B. $x_0={\log }_{21}8$

C. $x_0={\log }_{21}3$

D. $x_o={\log }_{9}7$

Câu 6 . Cho hình trụ có diện tích xung quanh bằng $50\pi$ và độ dài đường sinh bằng bán kính đường tròn đáy. Tính diện tích toàn phần của hình trụ.

A. $60\pi$

B. $80\pi$

C. $100\pi$

D. $120\pi$  

Câu 7 : Hàm số nào sau đây có đồ thị như hình vẽ bên?

A. $y={\displaystyle \frac{-x+3}{x+1}}$

B. $y={\displaystyle \frac{x-2}{x+1}}$

C. $y={\displaystyle \frac{x+2}{x-1}}$

D. $y={\displaystyle \frac{x+2}{x+1}}$

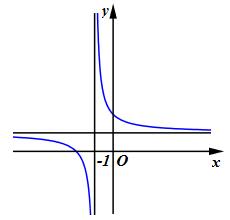
Câu 8 : Cho m, n là các số thực tùy ý và a là số thực dương khác 1. Mệnh đề nào sau đây đúng?

A. $a^m.a^n=a^{m.n}$

B. $a^m+a^n=a^{m+n}$

C. $a^{m-n}={\displaystyle \frac{a^m}{a^n}}$

D. $a^{m.n}=a^{{\displaystyle \frac{m}{n}}}$

Câu 9 : Tính đạo hàm y’ cuat hàm số $y=7^{x+3}$

A. $y^{\prime }=7^{x+3}$

B. $y^{\prime }=7^{x+2}\ln 7$

C. $y^{\prime }=7^{x+3}\ln 7$

D. $y^{\prime }={\displaystyle \frac{7^x}{\ln 7}}$

Câu 10 : Tìm tiệm cận ngang của đồ thị hàm số $y=1+{\displaystyle \frac{x-1}{x+1}}$

A. $y=2$

B. $y=1$

C.  $x=-1$

D. $x=1$

Câu 11 : Số cạnh của hình bát diện đều là:

A. 8

B. 10

C. 12

D. 24

Câu 12 : Cho hàm số $y=x^3-3x^2+1$. Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng $\left(0;2\right)$

B. Hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };0\right)$

C. Hàm số đồng biến trên khoảng $\left(0;2\right)$

D. Hàm số đồng biến trên R.

Câu 13 : Cho x, y là các số thực thỏa mãn ${\log }_2{\displaystyle \frac{y}{2\sqrt{1+x}}}=3\left(y-\sqrt{1+x}\right)-y^2+x$. Tính giá trị nhỏ nhất của biểu thức $K=x-y$ ?

A. $minK=-{\displaystyle \frac{3}{4}}$

B. $minK=-{\displaystyle \frac{5}{4}}$

C. $minK=-2$

D. $minK=-1$

Câu 14 : Cho khối chóp tứ giác đều S.ABCD có cạnh bên bằng 6, góc giữa đường thẳng SA và BC bằng 60⁰. Tính thể tích V của khối chóp S.ABCD?

A. $V=36$

B. $V=18$

C. $V=36\sqrt{2}$

D. $V=18\sqrt{3}$

Câu 15 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B; SA vuông góc với mặt phẳng (ABC) và $AB=6$. Một mặt phẳng $\left(\alpha \right)$ đi qua A vuông góc với SC cắt đoạn SC tại M và cắt đoạn SC tại N. Tính diện tích mặt cầu ngoại tiếp tứ diện ACMN?

A. $108\pi$

B. $36\pi$

C. $27\pi$

D. $72\pi$

Câu 16 : Cho $\left(S\right)$ là mặt cầu có đường kính $AB=10$. Vẽ các tiếp tuyến Ax, By với mặt cầu (S) sao cho $Ax\mathrm{\perp }By$. Gọi M là điểm di động trên Ax, N là điểm di động trên By sao cho MN luôn tiếp xúc với mặt cầu $\left(S\right)$. Tính giá trị của tích $AM.BN$.

A. $AM.BN=20$

B. $AM.BN=50$

C. $AM.BN=100$

D. $AM.BN=10$

Câu 17 : Đồ thị hàm số $y={\displaystyle \frac{2x+2}{x^2-3x-4}}$ có bao nhiêu đường tiệm cận?

A. 3

B. 1

C. 2

D. 4

Câu 18 : Tập xác định D của hàm số $y={\left(3x-6\right)}^{-3}$ là:

A. $D=\left(2;+\mathrm{\infty }\right)$

B. $D=\left[2;+\mathrm{\infty }\right)$

C. $D=R\mathrm{\setminus }\left\{2\right\}$

D. $D=R$

Câu 19 : Hàm số nào sau đây có đồ thị như hình vẽ bên?

A. $y=x^3-3x-1$

B. $y=-x^3+3x+1$

C. $y=x^3+6x^2+9x+1$

D. $y=x^4+3x^2+1$

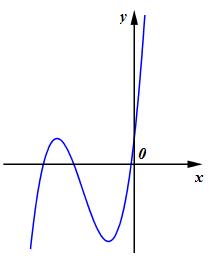
Câu 20 : Cho biểu thức $P=x\sqrt[3]{x^4}$ với $x>0$. Mệnh đề nào dưới đây đúng?

A. $P=x^{{\displaystyle \frac{7}{3}}}$

B. $P=x^{{\displaystyle \frac{5}{3}}}$

C. $P=x^{{\displaystyle \frac{7}{4}}}$

D. $P=x^{{\displaystyle \frac{6}{5}}}$

Câu 21 : Giá trị lớn nhất M của hàm số $y=x^4+3x^2-5$ trên đoạn $\left[-2;\sqrt{2}\right]$ là:

A. $M=23$

B. $M=25$

C. $M=5$

D. $M=28$

Câu 22 : Một mặt cầu có diện tích $16\pi$. Tính bán kính của mặt cầu?

A. $R=2\pi$

B. $R=2$

C. $R=4$

D. $R=4\pi$

Câu 23 : Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/ năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra?

A. 9 năm

B. 11 năm

C. 12 năm

D. 10 năm

Câu 24 : Một bác thợ muốn chế tạo một chiếc thùng đựng nước hình trụ, mặt xung quanh của thùng nước được cuộn từ những tấm nhôm hình chữ nhật có chu vi 4,8m. Hỏi bác thợ phải chọn tấm tôn có kích thước như thế nào để chiếc thùng đựng được nhiều nước nhất?

 

A. 1,2m và 1,2m

B. 1,6m và 0,8m

C. 1,8m và 0,6m

D. 1,4m và 1,0m

Câu 25 : Cho tam giác ABC vuông tại A có $AB=6,AC=8$. Quay tam giác ABC quanh trục AB ta nhận được hình nón có độ dài đường sinh bằng:

A. 8

B. 10

C. 6

D. 7

Câu 26 : Cho hai hàm số $y={\log }_{a}x$ và $y={\log }_{b}x$ có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?

A. $a>b>1$

B. $a>1>b$

C. $b>a>1$

D. $b>1>a$

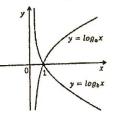
Câu 27 : Hình lập phương có bao nhiêu mặt đối xứng?

A. 6

B. 9

C. 8

D. 12

Câu 28 : Cho hàm số $y=a^x$ với $a>0,a\ne 1$. Mệnh đề nào sau đây sai?

A. Hàm số có tập xác định $D=R$

B. Hàm số có miền giá trị là $\left(0;+\mathrm{\infty }\right)$

B. Đồ thị hàm số có tiệm cận ngang là $y=0$

D. Đồ thị hàm số có tiệm cận đứng là $x=0$.

Câu 29 : Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là mệnh đề đúng?

A. $y_{CD}=1$

B. $y_{CD}=3$

C.  $\underset{x\in R}{min}y=-4$

D.  $\underset{x\in R}{max}y=3$

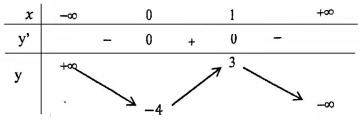
Câu 30 : Có bao nhiêu số nguyên m để phương trình $m\left(\sqrt{4-x}+\sqrt{5-x}\right)=x\sqrt{x}+3$ (m là tham số) có nghiệm?

A. 11

B. 5

C. 7

D. 14

Câu 31 : Cho hình chữ nhật ABCD có $AB=3AD=6$. Quay hình chữ nhât ABCD lần lượt quanh AD và AB, ta được hai khối tròn xoay có thể tích lần lượt là V₁ và V₂. Mệnh đề nào sau đây đúng?

A. $V_1=V_2$

B. $2V_1=V_2$

C. $V_1=2V_2$

D. $V_1=3V_2$

Câu 32 : Giả sử ${\log }_{2}7=a$. Tính giá trị của biểu thức $P={\log }_{14}8$ theo a?

A. $P=3\left(a+1\right)$

B. $P={\displaystyle \frac{3}{a+1}}$

C. $P=3a+1$

D. $P={\displaystyle \frac{1}{a+1}}$

Câu 33 : Cho hàm số $y=-3x^3+x-2$ có đồ thị $\left(C\right)$. Gọi E là giao điểm của đồ thị $\left(C\right)$ với trục tung. Viết phương trình tiếp tuyến với đồ thị $\left(C\right)$ tại điểm E.

A. $y=x-2$

 B. $y=-x+2$

C. $y=x+2$

D. $y=-x-2$

Câu 34 : Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng 6.

A. $V=54\sqrt{3}$

B. $V=18\sqrt{3}$

C. $V=27\sqrt{3}$

D. $V=12\sqrt{3}$

Câu 35 : Cho phương trình ${\log }^{2}x-\left(2m-3\right)\log x-m-1=0$ với m là tham số. Tìm các giá trị của tham số m để phương trình có hai nghiệm x₁, x₂ thỏa mãn $x_1{x}_2=10$.

A. $m={\displaystyle \frac{3}{2}}$

B. $m=11$

C. $m=\frac{13}{2}$

D. $m=2$.

Câu 36 : Cho khối lăng trụ tam giác ABC.A’B’C’ có thể tích bằng 30. Tính thể tích khối chóp A.BCC’B’

A. 20

B. 10

C. 25

D. 15

Câu 37 : Hàm số $y=x^4+2x^2-3$ có đồ thị là hình vẽ sau đây?

 

Câu 38 : Tập xác định của hàm số $y={\log }_{0,3}{\displaystyle \frac{-2x+4}{x+3}}$ là :

A. $D=\left(-\mathrm{\infty };-3\right)\cup \left(2;+\mathrm{\infty }\right)$

B. $D=\left(0;2\right)$

C. $D=\left(-3;2\right]$

D. $D=\left(-3;2\right)$

Câu 39 : Cho hàm số $y=2x^3+3m{x}^2+3x+m^2$  (m là tham số). Gọi S là tập hợp tất cả các số nguyên m trong khoảng $\left(-10;10\right)$ để đồ thị hàm số có hai điểm cực trị nằm về hai phía của đường thẳng $y=3x-4$. Tìm số phần tử của tập S.

A. 19

B. 18

C. 8

D. 11

Câu 40 : Tính tổng các nghiệm của phương tình ${3.4}^{x+1}-{35.6}^x+{2.9}^{x+1}=0$.

A. $2-{\log }_{2}3$

B. 4

C. $-1$

D. $2+{\log }_{2}3$

Câu 41 : Cho tứ diện ABCD có $AB=5,AC=3,BC=4,BD=4,$$AD=3$ và $CD={\displaystyle \frac{12}{5}}\sqrt{2}$. Tính thể tích V của khối tứ diện ABCD ?

A. $V={\displaystyle \frac{24}{5}}$

B. $V={\displaystyle \frac{24}{5}}\sqrt{2}$

C. $V={\displaystyle \frac{19}{3}}$

D. $V={\displaystyle \frac{19}{3}}\sqrt{2}$

Câu 42 : Biết n là một số tự nhiên thỏa mãn đẳng thức ${\displaystyle \frac{1}{{\log }_{2}n}}+{\displaystyle \frac{1}{{\log }_{3}n}}+{\displaystyle \frac{1}{{\log }_{4}n}}=1$. Số tự nhiên nào sau đây là bội của n?

A. 48

B. 45

C. 6

D. 9

Câu 43 : Hàm số nào sau đây đồng biến trên khoảng $\left(-\mathrm{\infty };+\mathrm{\infty }\right)$?

A. $y=2$

B. $y=-x^3-3x$

C. $y={\displaystyle \frac{x+1}{x+2}}$

D. $y=x^3-3x^2+3$

Câu 44 : Tìm tất cả các giá trị của m để hàm số $y={\displaystyle \frac{mx-1}{x+m}}$ đạt giá trị lớn nhất trên đoạn $\left[1;3\right]$ bằng 2.

A. $m=-3$

B. $m=7$

C. $m=3$

D. $m=2$

Câu 45 . Hàm số $y=x^3-3x^2+3$ có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình $\left|x^3-3x^2+3\right|=m$ có bốn nghiệm thực phân biệt.

A. $0<m<3$

B. $1<m<3$

C. $-1<m<3$

D. $0<m<1$

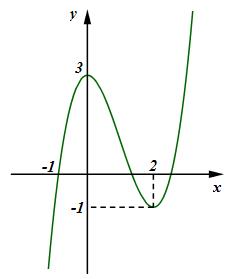
Câu 46 : Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA vuông góc với đáy (ABC) và $SC=a\sqrt{3}$. Tính thể tích khối chóp S.ABC theo a?

A. ${\displaystyle \frac{2a^3\sqrt{6}}{9}}$

B. ${\displaystyle \frac{a^3\sqrt{6}}{12}}$

C. ${\displaystyle \frac{a^3\sqrt{3}}{4}}$

D. ${\displaystyle \frac{a^3\sqrt{3}}{2}}$

Câu 47 : Cho khối trụ $\left(T\right)$ có O và O’ là tâm hai đường tròn đáy. Gọi $AB{B}^{\prime }{A}^{\prime }$ là thiết diện song song với trục $O{O}^{\prime }$ (A, B thuộc đường tròn O; A’, B’ thuộc đường tròn O’). Biết $AB=8,A{A}^{\prime }=6$ và thể tích của khối trụ $\left(T\right)$ bằng $150\pi$. Tính khoảng cách từ O đến mặt phẳng (ABB’A’).

A. $d=5$

B. $d=2$

C. $d=3$

D. $d=4$.

Câu 48 : Giả sử đồ thị hàm số $y=x^3-3x^2+4$ có hai điểm cực trị A và B. Diện tích S của tam giác OAB với O là gốc tọa độ bằng:

A. $S=7$

B. $S=8$

C. $S=4$

D. $S=14$

Câu 49 : Gọi S là tập hợp tất cả các số nguyên m để hàm số $y={\displaystyle \frac{mx-4m-5}{x-m}}$ (m là tham số) đồng biến trên khoảng $\left(0;2\right)$. Tìm số phần tử của S.

A. $5$

B. Vô số

C. 4

D. 7

Câu 50 : Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật $AB=a,AD=a\sqrt{3}$. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm A đến mặt phẳng (SCD) bằng $a\sqrt{2}$. Tính thể tích khối chóp S.ABCD theo a?

A. $a^3\sqrt{2}$

B. $a^3\sqrt{3}$

C. $2a^3$

D. $a^3\sqrt{6}$

Lời giải chi tiết

1. A	2. C	3. C	4. B	5. D
6. D	7. D	8. C	9. C	10. A
11. C	12. A	13. B	14. C	15. D
16. B	17. C	18. C	19. C	20. A
21. A	22. B	23. B	24. B	25. B
26. B	27. B	28. D	29. B	30. A
31. D	32. B	33. A	34. A	35. D
36. A	37. D	38. D	39. C	40. C
41. A	42. A	43. D	44. B	45. B
47. C	48. C	48. C	49. C	50. A

Bộ Đề thi Toán lớp 12 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 10

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 12

Thời gian làm bài: 90 phút

(Đề 10)

Câu 1  : Cho hàm số $y=x^4-2m{x}^2+m\left(C\right)$ với $m$là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm tham số $m$ để tiếp tuyến $\mathrm{\Delta }$ với đồ thị (C) tại A cắt đường tròn $\left(T\right):x^2+{\left(y-1\right)}^2=4$ tạo thành một dây cung có độ dài nhỏ nhất.

A. $m={\displaystyle \frac{16}{13}}$

B. $m=-{\displaystyle \frac{13}{16}}$

C. $m={\displaystyle \frac{13}{16}}$

D. $m=-{\displaystyle \frac{16}{13}}$

Câu 2  : Có bao nhiêu loại khối đa điện đều mà mỗi mặt của nó là một tam giác đều?

A. 3.

B. 1.

C. 5.

D. 2.

Câu 3  : Cho hàm số $y=f(x)$ có đồ thị $y=f^{\prime }(x)$ cắt trục Ox tại ba điểm có hoành độ $a<b<c$ như hình vẽ.

Xét 4 mệnh đề sau:

$\left(1\right):f(c)>f(a)>f(b).$                   

$\left(2\right):f(c)>f(b)>f(a).$

$\left(3\right):f(a)>f(b)>f(c).$             

$\left(4\right):f(a)>f(b).$

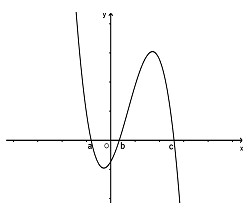
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?

A. 4.

B. 1.

C. 2.

D. 3.

Câu 4  : Cho một đa giác đều $2n$ đỉnh $(n\ge 2,n\in N)$. Tìm n  biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số $2n$ đỉnh của đa giác đó là 45.

A. $n=12$.

B. $n=10$.

C. $n=9$.

D. $n=45$.

Câu 5  : Cho $\underset{-1}{\overset{5}{\int }}f\left(x\right)dx=4$. Tính $I=\underset{-1}{\overset{2}{\int }}f\left(2x+1\right)dx$.

A. $I=2.$

B. $I={\displaystyle \frac{5}{2}}.$

C. $I=4.$

D. $I={\displaystyle \frac{3}{2}}.$

Câu 6  : Trong không gian với hệ tọa độ $Oxyz$, cho hai mặt phẳng $\left(P\right):x+\left(m+1\right)y-2z+m=0$ và $\left(Q\right):2x-y+3=0$, với $m$ là tham số thực. Để $\left(P\right)$ và $\left(Q\right)$ vuông góc thì giá trị của $m$ bằng bao nhiêu?

A. $m=-5$.

B. $m=1$.

C. $m=3$.

D. $m=-1$.

Câu 7  : Cho bốn mệnh đề sau:

$(I):\int {\cos }^{2}x\mathrm{d}x={\displaystyle \frac{{\cos }^{3}x}{3}}+C$

$(II):\int {\displaystyle \frac{2x+1}{x^2+x+2018}}\mathrm{d}x$$=\ln \left(x^2+x+2018\right)+C$

$(III):\int 3^x\left(2^x+3^{-x}\right)\mathrm{d}x$$={\displaystyle \frac{6^x}{\ln 6}}+x+C$   

$(IV):\int 3^x\mathrm{d}x=3^x.\ln 3+C$

Trong các mệnh đề trên có bao nhiêu mệnh đề sai?

A. 3

B. 1

C. 2

D. 4

Câu 8  : Cho hình chóp $S.ABC$ có $SA$ vuông góc mặt phẳng $(ABC)$, tam giác $ABC$ vuông tại $B$. Biết $SA=2a,AB=a,BC=a\sqrt{3}$. Tính bán kính $R$ của mặt cầu ngoại tiếp hình chóp đã cho.

A. $a$.

B. $2a$.

C. $a\sqrt{2}$.

D. $2a\sqrt{2}$.

Câu 9  : Cho hàm số $y={\displaystyle \frac{2x-1}{x-1}}$ có đồ thị  (C). Tìm tất cảc các giá trị thực của tham số m để đường thẳng $d:y=x+m$  và cắt (C) tại hai điểm phân biệt A, B sao cho $AB=4$.

A. $m=-1$

B. $[\begin{array}{c}m=0\\ m=3\end{array}$

C. $[\begin{array}{c}m=-1\\ m=3\end{array}$

D. $m=4$

Câu 10  : Tìm tập xác định $D$ của hàm số $y={\displaystyle \frac{\tan x-1}{\sin x}}+\cos \left(x+{\displaystyle \frac{\pi }{3}}\right).$

A. $D=R\mathrm{\setminus }\left\{k\pi ,k\in Z\right\}$

B. $D=R\mathrm{\setminus }\left\{{\displaystyle \frac{k\pi }{2}},k\in Z\right\}$

C. $D=R\mathrm{\setminus }\left\{{\displaystyle \frac{\pi }{2}}+k\pi ,k\in Z\right\}$

D. $D=R$

Câu 11  : Khẳng định nào sau đây là khẳng định sai?

A. $\cos x=-1\iff x=\pi +k2\pi .$

B. $\cos x=0\iff x={\displaystyle \frac{\pi }{2}}+k\pi .$

C. $\cos x=1\iff x=k2\pi .$

D. $\cos x=0\iff x={\displaystyle \frac{\pi }{2}}+k2\pi .$

Câu 12  : Tập nghiệm của phương trình  $9^x-{4.3}^x+3=0$ là

A. $\left\{0;1\right\}$

B. $\left\{1;3\right\}$

C. $\left\{0;-1\right\}$

D. $\left\{1;-3\right\}$

Câu 13  : Cho hình chóp $S.ABCD$ có đáy ABCD là hình bình hành thỏa mãn $AB=a,AC=a\sqrt{3},BC=2a$. Biết tam giác SBC cân tại S, tam giác SCD vuông tại C  và khoảng cách từ D đến mặt phẳng $\left(SBC\right)$ bằng ${\displaystyle \frac{a\sqrt{3}}{3}}$. Tính thể tích V  của khối chóp đã cho.

A. $V={\displaystyle \frac{2a^3}{3\sqrt{5}}}$.

B. ${\displaystyle \frac{a^3}{3\sqrt{5}}}$.

C. $V={\displaystyle \frac{a^3}{3\sqrt{3}}}$.

D. ${\displaystyle \frac{a^3}{\sqrt{5}}}$.

Câu 14  : Trong không gian với hệ tọa độ $Oxyz$, mặt cầu $\left(S\right):x^2+y^2+z^2-4x+2y-6z+4$$=0$ có bán kính $R$ là

A. $R=\sqrt{53}$.

B. $R=4\sqrt{2}$.

C. $R=\sqrt{10}$.

D. $R=3\sqrt{7}$

Câu 15  : Một người dùng một cái ca hình bán cầu (Một nửa hình cầu) có bán kính là $3\mathrm{c}\mathrm{m}$để múc nước đổ vào một cái thùng hình trụ chiều cao $10\mathrm{c}\mathrm{m}$ và bán kính đáy bằng $6\mathrm{c}\mathrm{m}$. Hỏi người ấy sau bao nhiêu lần đổ thì nước đầy thùng? (Biết mỗi lần đổ, nước trong ca luôn đầy.)

A. 10 lần.

B. 24 lần.

C. 12 lần.           

D. 20 lần.

 

Câu 16  : Cho hàm số $f\left(x\right)$ có đạo hàm liên tục trên R và có đồ thị của hàm $y=f^{\prime }\left(x\right)$ như hình vẽ. Xét hàm số $g(x)=f\left(2-x^2\right)$. Mệnh đề nào dưới đây đúng ?

A. Hàm số $f(x)$ đạt cực trị tại $x=2$

B. Hàm số $f(x)$nghịch  biến trên $\left(-\mathrm{\infty };2\right).$

C. Hàm số $g(x)$ đồng biến trên $\left(2;+\mathrm{\infty }\right).$

D. Hàm số$g(x)$ngịch biến trên $\left(-1;0\right).$

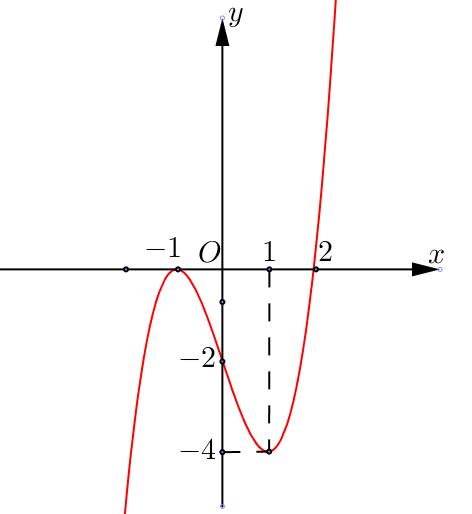
Câu 17  : Tìm tham số m để hàm số $y={\displaystyle \frac{1}{3}}{x}^3-m{x}^2+\left(m+2\right)x+2018$ không có cực trị.

A. $m\le -1$  hoặc  $m\ge 2$

B. $m\le -1$

C. $m\ge 2$

D. $-1\le m\le 2$

Câu 18  : Hàm số nào sau đây đồng biến trên $\mathbb{R}?$

A. $y=-x\sqrt{2}+1$

B. $y=x^3-3x+1$.

C. $y=x^2+1$ .

D. $y=x^3+3x+1$ .

Câu 19  : Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng $3a$. Tính diện tích toàn phần của hình trụ đã cho.

A. $9a^2\pi$

B. ${\displaystyle \frac{9\pi a^2}{2}}$

C. ${\displaystyle \frac{13\pi a^2}{6}}$

D. ${\displaystyle \frac{27\pi a^2}{2}}$

Câu 20  : Tìm tập xác định của hàm số $f\left(x\right)={\left(1+\sqrt{x-1}\right)}^{\sqrt{5}}$.

A. $D=\mathbb{R}$

B. $D=\left[1;+\mathrm{\infty }\right)$

C. $D=\left(0;+\mathrm{\infty }\right)$

D. $D=\mathbb{R}\mathrm{\setminus }\left\{1\right\}$

Câu 21  : Cho hai số phức $z_1=2+3i$ và $z_2=-3-5i$. Tính tổng phần thực và phần ảo của số phức $w=z_1+z_2$.

A. $3$.

B. 0.

C. $-1-2i$.

D. $-3$.

Câu 22  : Cho hàm số $y=x\ln x$. Chọn khẳng định sai trong số các khẳng định sau:

A. Hàm số đồng biến trên khoảng $\left(0;+\mathrm{\infty }\right)$ .

B. Hàm số đồng biến trên khoảng $\left({\displaystyle \frac{1}{e}};+\mathrm{\infty }\right)$.

C. Hàm số có đạo hàm $$.

D. Hàm số có tập xác định là $D=\left(0;+\mathrm{\infty }\right)$.

Câu 23  : Có bao nhiêu số tự nhiên có ba chữ số dạng $\overline{abc}$ với $a,b,c\in \left\{0,1,2,3,4,5,6\right\}$ sao cho $a<b<c$ .

A. 120.

B. 30.

C. 40.

D. 20.

Câu 24  : Cho lăng trụ đứng $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có $A{A}^{\prime }=a$, đáy ABC là tam giác vuông cân tại A và $AB=a$. Tính thể tích V của khối lăng trụ đã cho.

A. $V={\displaystyle \frac{a^3}{2}}.$

B. $V=a^3.$

C. $V={\displaystyle \frac{a^3}{3}}.$

D. $V={\displaystyle \frac{a^3}{6}}.$

Câu 25  : Tính đạo hàm của hàm số$y={\log }_2\left(x+e^x\right)$.

A. ${\displaystyle \frac{1+e^x}{\ln 2}}$

B. ${\displaystyle \frac{1+e^x}{\left(x+e^x\right)\ln 2}}$

C. ${\displaystyle \frac{1+e^x}{x+e^x}}$

D. ${\displaystyle \frac{1}{\left(x+e^x\right)\ln 2}}$

Câu 26  : Cho tam giác $ABC$ vuông tại $A$, $AB=6\mathrm{c}\mathrm{m}$, $AC=8\mathrm{c}\mathrm{m}$. Gọi $V_1$ là thể tích khối nón tạo thành khi quay tam giác $ABC$ quanh cạnh $AB$ và $V_2$ là thể tích khối nón tạo thành khi quay tam giác $ABC$ quanh cạnh $AC$. Khi đó, tỷ số ${\displaystyle \frac{V_1}{V_2}}$ bằng

A. ${\displaystyle \frac{16}{9}}$.

B. ${\displaystyle \frac{4}{3}}$.

C. ${\displaystyle \frac{3}{4}}$.

D. ${\displaystyle \frac{9}{16}}$.

Câu 27  : Cho hàm số $f\left(x\right)$ có đạo hàm là $f^{\prime }\left(x\right)=\left(x^2-1\right){\left(x-\sqrt{3}\right)}^2$. Số điểm cực trị của hàm số này là

A. 1.

B. 2.

C. 3.

D. 4.

Câu 28  : Xét các số thực $a,b$thỏa mãn điều kiện ${\displaystyle \frac{1}{3}}<b<a<1$. Tìm giá trị nhỏ nhất của biểu thức $P={\log }_a\left({\displaystyle \frac{3b-1}{4}}\right)+12{\log }_{{\displaystyle \frac{b}{a}}}^{2}a-3$ .

A. $\mathrm{M}\mathrm{i}\mathrm{n}P=13.$

B. $Min\mathrm{P}={\displaystyle \frac{1}{\sqrt[3]{2}}}.$

C. $Min\mathrm{P}=9$

D. $\mathrm{P}=\sqrt[3]{2}$

Câu 29  : Cho hình phẳng D giới hạn bởi  đường cong $y=\sqrt{2+\cos x}$, trục hoành và các đường thẳng $x=0,x={\displaystyle \frac{\pi }{2}}$. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V  bằng bao nhiêu ?

A. $V=\pi -1$.

B. $V=\pi +1$

C. $V=\pi \left(\pi -1\right)$

D. $V=\pi \left(\pi +1\right)$

Câu 30  : Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt.

A. Năm mặt.

B. Ba mặt.

C. Bốn mặt.

D. Hai mặt.

Câu 31  : Giải phương trình $\cos 2x+5\sin x-4=0.$

A. $x={\displaystyle \frac{\pi }{2}}+k\pi .$

B. $x=-{\displaystyle \frac{\pi }{2}}+k\pi .$

C. $x=k2\pi .$

D. $x={\displaystyle \frac{\pi }{2}}+k2\pi .$

Câu 32  : Tìm giá trị lớn nhất của hàm số $f\left(x\right)=x^3-3x^2-9x+10$ trên $\left[-2;2\right]$.

A. $\underset{[-2;2]}{max}f(x)=17$

B. $\underset{[-2;2]}{max}f(x)=-15$

C. $\underset{[-2;2]}{max}f(x)=15$

D. $\underset{[-2;2]}{max}f(x)=5$

Câu 33  : Một tổ có $6$ học sinh nam và $9$ học sinh nữ. Hỏi có bao nhiêu cách chọn $6$ học sinh đi lao động, trong đó $2$ học sinh nam?

A. $C_6^2+C_9^4$.

B. $C_6^2.C_9^4$.

C. $A_6^2.A_9^4$.

D. $C_9^2.C_6^4$.

Câu 34  : Cho số phức $z$ thỏa mãn $z+4\overline{z}=7+i\left(z-7\right)$. Khi đó, môđun của $z$ bằng bao nhiêu?

A. $\left|z\right|=5$.

B. $\left|z\right|=\sqrt{3}$.

C. $\left|z\right|=\sqrt{5}$.

D. $\left|z\right|=3$.

Câu 35  : Cho khối lăng trụ đứng $ABC.A^{\prime }{B}^{\prime }{C}^{\prime }$ có đáy là tam giác đều. Mặt phẳng $\left(A^{\prime }BC\right)$ tạo với đáy góc ${30}^0$ và tam giác $A^{\prime }BC$ có diện tích bằng $8a^2$. Tính thể tích V của khối lăng trụ đã cho.

A. $V=8\sqrt{3}{a}^3.$

B. $V=2\sqrt{3}{a}^3.$

C. $V=64\sqrt{3}{a}^3.$

D. $V=16\sqrt{3}{a}^3.$

Câu 36  : Cho các chữ số 0, 1, 2, 3, 4, 5 . Từ các chữ số đã cho lập được bao nhiêu số tự nhiên chẵn có 4 chữ số và các chữ số đôi một bất kỳ khác nhau.

A. 160 .

B. 156 .

C. 752 .

D. 240 .

Câu 37  : Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $M(0;-1;2)$ và $N(-1;1;3)$. Một mặt phẳng $\left(P\right)$ đi qua M, N sao cho khoảng cách từ điểm $K\left(0;0;2\right)$. đến mặt phẳng $\left(P\right)$ đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến $\overrightarrow{n}$ của mặt phẳng (P).

A. $\overrightarrow{n}\left(1;-1;1\right)$

B. $\overrightarrow{n}\left(1;1;-1\right)$

C. $\overrightarrow{n}\left(2;-1;1\right)$

D. $\overrightarrow{n}\left(2;1;-1\right)$

Câu 38  : Cho số phức $z$ thỏa mãn $\left(1+3i\right)z-5=7i$. Mệnh đề nào sau đây là mệnh đề đúng?

A. $\overline{z}=-{\displaystyle \frac{13}{5}}+{\displaystyle \frac{4}{5}}i$.

B. $\overline{z}={\displaystyle \frac{13}{5}}-{\displaystyle \frac{4}{5}}i$.

C. $\overline{z}=-{\displaystyle \frac{13}{5}}-{\displaystyle \frac{4}{5}}i$.

D. $\overline{z}={\displaystyle \frac{13}{5}}+{\displaystyle \frac{4}{5}}i$.

Câu 39  : Cho  số phức $z$ và $w$ thỏa mãn $z+w=3+4i$ và $\left|z-w\right|=9$. Tìm giá trị lớn nhất của biểu thức $T=\left|z\right|+\left|w\right|$.

A. $MaxT=\sqrt{176}$

B. $MaxT=14$

C. $MaxT=4$

D. $MaxT=\sqrt{106}$

Câu 40  : Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức $z_1=-1+i,$ $z_2=1+2i,z_3=2-i,z_4=-3i$. Gọi S diện tích tứ giác ABCD. Tính S.

A. $S={\displaystyle \frac{17}{2}}$

B. $S={\displaystyle \frac{19}{2}}$

C. $S={\displaystyle \frac{23}{2}}$

D. $S={\displaystyle \frac{21}{2}}$

Câu 41  : Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bởi hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía ngoài ta được hình 2. Khi quay hình 2 xung quanh trục $d$ ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.

 

A. ${\displaystyle \frac{5\pi \sqrt{3}}{3}}$

B. ${\displaystyle \frac{9\pi \sqrt{3}}{8}}$

C. ${\displaystyle \frac{7\pi \sqrt{3}}{6}}$.

D. ${\displaystyle \frac{5\pi \sqrt{3}}{2}}$

Câu 42  : Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $M\left(2;-3;5\right)$, $N\left(6;-4;-1\right)$ và đặt $L=\left|\overrightarrow{MN}\right|$. Mệnh đề nào sau đây là mệnh đề đúng?

A. $L=\left(4;-1;-6\right)$.

B. $L=\sqrt{53}$.

C. $L=3\sqrt{11}$.

D. $L=\left(-4;1;6\right)$.

Câu 43  : Tìm tham số m để phương trình ${\log }_{\sqrt{2018}}\left(x-2\right)={\log }_{2018}\left(mx\right)$ có nghiệm thực duy nhất.

A. $1<m<2$

B. $m>1$

C. $m>0$

D. $m<2$

Câu 44  : Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $(P):x-2y+2z-2=0$ và điểm $I(-1;2;-1)$. Viết phương trình mặt cầu $(S)$ có tâm $I$ và cắt mặt phẳng $(P)$ theo giao tuyến là đường tròn có bán kính bằng 5.

A. $(S):(x+1{)}^2+(y-2{)}^2+(z+1{)}^2=25$.

B. $(S):(x+1{)}^2+(y-2{)}^2+(z+1{)}^2=16$.

C. $(S):(x-1{)}^2+(y+2{)}^2+(z-1{)}^2=34$.

D. $(S):(x+1{)}^2+(y-2{)}^2+(z+1{)}^2=34$.

Câu 45  : Trong không gian với hệ tọa độ $Oxyz$, mặt phẳng chứa hai điểm $A\left(1;0;1\right)$, $B(-1;2;2)$ và song song với trục $Ox$ có phương trình là:

A. $y--2z+2=0$.

B. $x+2z--3=0$.

C. $2y--z+1=0$.

D. $x+y--z=0$.

Câu 46  : Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d$ vuông góc với mặt phẳng $(P):4x-z+3=0$. Véc-tơ nào dưới đây là một véctơ chỉ phương của đường thẳng d ?

A. $\overrightarrow{u_1}(4;1;-1)$

B. $\overrightarrow{u_2}(4;-1;3)$.

C. $\overrightarrow{u_3}(4;0;-1)$.

D. $\overrightarrow{u_4}(4;1;3)$.

Câu 47  : Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A(a;0;0)$, $B(0;b;0)$, $C(0;0;c)$ với

a,b,c  là các số thực dương thay đổi tùy ý sao cho $a^2+b^2+c^2=3$. Khoảng cách từ $O$ đến mặt

phẳng $(ABC)$ lớn nhất bằng:

A. ${\displaystyle \frac{1}{3}}$

B. 3

C. ${\displaystyle \frac{1}{\sqrt{3}}}$

D. 1

Câu 48  : Đường tiệm cận ngang của đồ thị hàm số $y=1+{\displaystyle \frac{2x+1}{x+2}}$ có phương trình là:

A. $x=-2$

B. $y=3$

C. $x=-1$

D. $y=2$

Câu 49  : Tìm nguyên hàm của hàm số $f\left(x\right)=\sin 3x.$

A. $\int \sin 3x\mathrm{d}x=-{\displaystyle \frac{\cos 3x}{3}}+C.$

B. $\int \sin 3x\mathrm{d}x={\displaystyle \frac{\cos 3x}{3}}+C.$

C. $\int \sin 3x\mathrm{d}x=-{\displaystyle \frac{\sin 3x}{3}}+C.$

D. $\int \sin 3x\mathrm{d}x=-\cos 3x+C.$

Câu 50  : Giải phương trình $\cos 5x.\cos x=cos4x.$

A. $x={\displaystyle \frac{k\pi }{5}}\left(k\in Z\right).$

B. $x={\displaystyle \frac{k\pi }{3}}\left(k\in Z\right).$

C. $x=k\pi \left(k\in Z\right).$

D. $x={\displaystyle \frac{k\pi }{7}}\left(k\in Z\right).$

Lời giải chi tiết

1. C	2. A	3. B	4. B	5. A
6. B	7. C	8. C	9. C	10. B
11. D	12. A	13. A	14. C	15. D
16. D	17. D	18. D	19. D	20. B
21. D	22. A	23. D	24. A	25. B
26. B	27. B	28. C	29. D	30. B
31. D	32. C	33. B	34. C	35. A
36. B	37. B	38. D	39. D	40. A
41. C	42. B	43. C	44. D	45. A
46. C	47. C	48. B	49. A	50. A