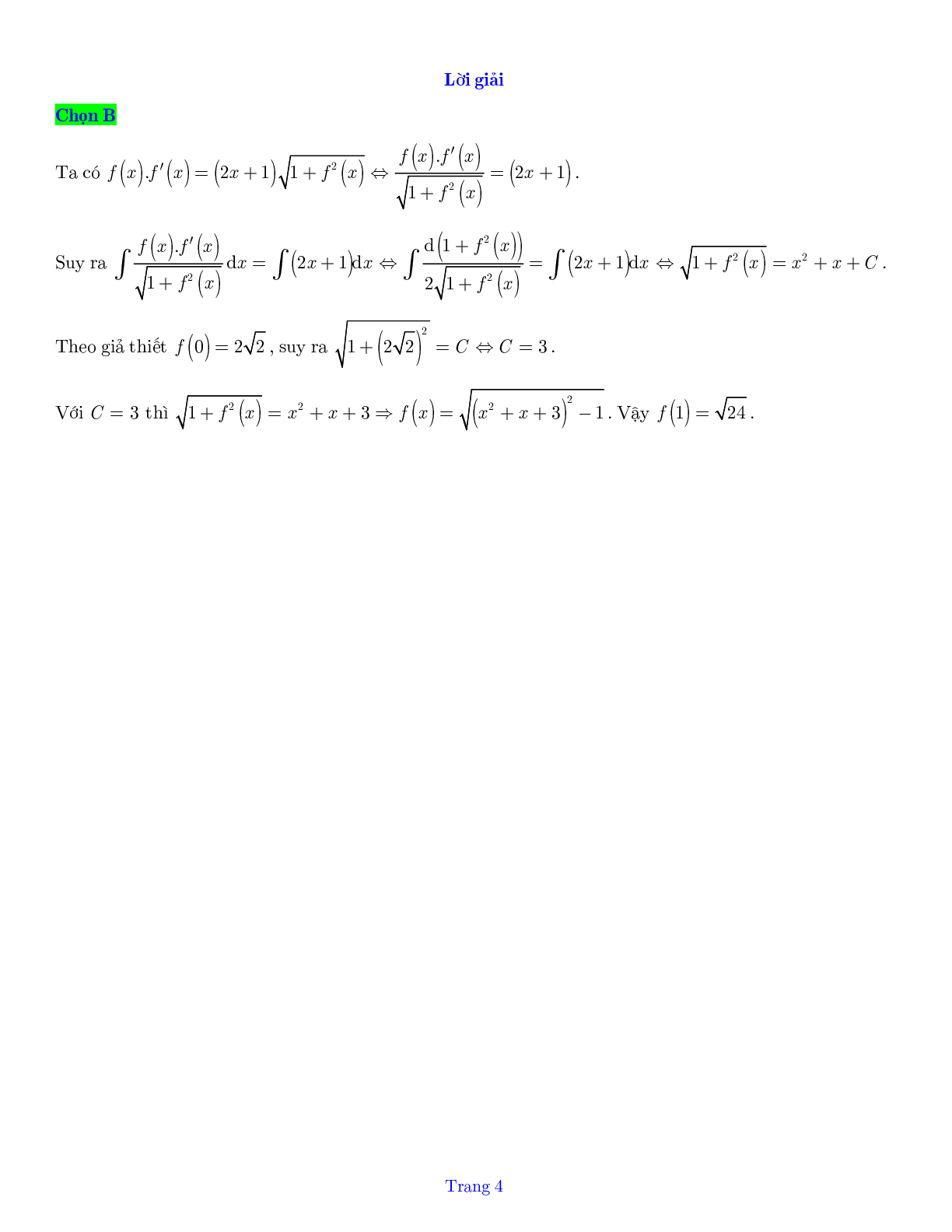Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Phân tích một số câu vận dụng trong đề minh họa THPTQG môn Toán năm 2020, tài liệu bao gồm 39 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Phân tích một số câu vận dụng trong đề minh họa THPTQG môn Toán năm 2020

Câu 38: Cho hàm số f(x) có f(3) = 3 và \[f'(x) = \frac{x}{{x + 1 - \sqrt {x + 1} }}\] với x > 0. Khi đó \[\int\limits_3^8 {f(x)dx} \]bằng

A. 7

B. \[\frac{{197}}{6}\]

C. \[\frac{{29}}{2}\]

D. \[\frac{{181}}{6}\]

Lời giải 1

f(8) – f(3) = \[\int\limits_3^8 {f'(x)dx = } \int\limits_3^8 {\frac{x}{{x + 1 - \sqrt {x + 1} }}dx = 7} \]

\[ \Rightarrow f(8) = 10.\]

\[\begin{array}{l}\int\limits_3^8 {f(x)dx}  = xf(x)\left| {\begin{array}{*{20}{c}}8\\3\end{array} - \int\limits_3^8 {xf'(x)dx} } \right.\\ = 8f(8) - 3f(3) - \int\limits_3^8 {\frac{{{x^2}}}{{x + 1 - \sqrt {x + 1} }}dx} \\ = 80 - 9 - \frac{{229}}{6} = \frac{{197}}{6}.\end{array}\]

Lời giải 2

Ta có

\[\begin{array}{l}f'(x) = \frac{x}{{x + 1 - \sqrt {x + 1} }}\\ = \frac{{\left( {\sqrt {x + 1}  + 1} \right)\left( {\sqrt {x + 1}  - 1} \right)}}{{\sqrt {x + 1} (\sqrt {x + 1}  - 1)}} = 1 + \frac{1}{{\sqrt {x + 1} }}\end{array}\]

Suy ra f(x) = x + \[2\sqrt {x + 1} \]+ C

Mà f(3) = 3 Þ C = -4. Do đó f(x) = x + \[2\sqrt {x + 1} \] - 4.

Vì vậy \[\int\limits_3^8 {\left( {x + 2\sqrt {x + 1}  - 4} \right)dx}  = \frac{{197}}{6}\].

Nhận xét: Với giả thiết như vậy ta có thể xử lý theo hai hướng:

Hướng 1: Tìm f (x) từ đó suy ra \[\int\limits_3^8 {f(x)dx} \]. Nếu để ý kỹ hơn thì thấy

\[\frac{x}{{x + 1 - \sqrt {x + 1} }} = \frac{{\left( {\sqrt {x + 1}  + 1} \right)\left( {\sqrt {x + 1}  - 1} \right)}}{{\sqrt {x + 1} (\sqrt {x + 1}  - 1)}} = 1 + \frac{1}{{\sqrt {x + 1} }}\]

Khi đó, có thể dễ dàng tìm f(x).

Hướng 2: Sử dụng tích phân từng phần

\[\begin{array}{l}\int\limits_3^8 {f(x)dx}  = xf(x)\left| {\begin{array}{*{20}{c}}8\\3\end{array} - \int\limits_3^8 {xf'(x)dx} } \right.\\ = 8f(8) - 3f(3) - \int\limits_3^8 {\frac{{{x^2}}}{{x + 1 - \sqrt {x + 1} }}dx} \end{array}\]

Như thế, chỉ cần tính f (8) là xong.

BÀI TẬP TƯƠNG TỰ CÂU 38

Câu 38.1: Cho hàm số f (x) liên tục trên (0;+ ¥). Biết \[f'(x) = \frac{{\ln x}}{x}\]và f(1) = 0. Giá trị \[\int\limits_1^e {f(x)dx} \]bằng

A. e – 2

B. \[\frac{1}{2}\]

C. \[\frac{1}{6}\]

D. \[\frac{{e - 2}}{2}\]

Lời giải

Chọn D

Ta có \[\int {f'(x)dx = \int {\frac{{\ln x}}{x}dx = \int {\ln xd(\ln x) = \frac{{{{\ln }^2}x}}{2} + C} } } \]

Nên \[f(x) = \frac{{{{\ln }^2}x}}{2} + C\], với C là hằng số .

Mà f(1) = 0 Þ C = 0 Þ f(x) = \[\frac{{{{\ln }^2}x}}{2}\]

Do đó, \[\int\limits_1^e {f(x)dx}  = \int\limits_1^e {\frac{{{{\ln }^2}x}}{2}} dx = \frac{{e - 2}}{2}.\]

Câu 38.2: Biết rằng xsinx là một nguyên hàm của hàm số f(-x ) trên R. Gọi F (x) là một nguyên hàm của hàm số \[\left[ {f'(x) + f'(\pi  - x)} \right]\cos x\]thỏa mãn F(0) = 0 . Giá trị của \[F\left( {\frac{\pi }{4}} \right)\] bằng

A. \[\pi \]

B. \[\frac{\pi }{4}\]

C. 0

D. \[\frac{\pi }{2}\]

Lời giải

Chọn D

xsinx là một nguyên hàm của hàm số f(- x) Þ f (-x) = \[{\left( {x\sin x} \right)^\prime }\]= sinx + xcosx

Þ f(x) = - sinx – xcosx

Þ \[{f^\prime }(x)\]= - 2cosx + xsinx

Þ \[{f^\prime }(\pi  - x)\]= 2cosx + (p - x)sinx

Þ \[{f^\prime }(x)\]+\[{f^\prime }(\pi  - x)\] = 2psinx

Khi đó

F(x) = \[\int {\left[ {{f^\prime }(x) + {f^\prime }(\pi  - x)} \right]\cos xdx = \pi } \int {2\sin x.\cos xdx} \]

\[ = \pi \int {\sin 2xdx}  =  - \frac{\pi }{2}cos2x + C\]

Từ F(0) = 0 Þ C = \[\frac{\pi }{2}\]Þ F(x) = - \[\frac{\pi }{2}\]cos2x +\[\frac{\pi }{2}\]Þ \[F\left( {\frac{\pi }{4}} \right)\]=\[\frac{\pi }{2}\].

Câu 38.3: Cho hàm số f (x) liên tục trên \[\mathbb{R}\] thỏa mãn các điều kiện:

f(0) = \[2\sqrt 2 \], f(x) > 0, \[\forall x \in \mathbb{R}\] và f(x). \[f'(x)\] = (2x + 1) \[\sqrt {x + {f^2}(x)} ,\forall x \in \mathbb{R}\].

Khi đó giá trị f (1) bằng

A. \[\sqrt {26} \]

B. \[\sqrt {24} \]

C. \[\sqrt {15} \]

D. \[\sqrt {23} \]

Lời giải

Chọn B

Ta có f(x). \[{f^\prime }(x)\] = (2x + 1) \[\sqrt {1 + {f^2}(x)} \]

\[ \Leftrightarrow \frac{{f(x).f'(x)}}{{\sqrt {1 + {f^2}(x)} }} = (2x + 1)\]

Suy ra

 \[\begin{array}{l}\int {\frac{{f(x).f'(x)}}{{\sqrt {1 + {f^2}(x)} }}dx}  = \int {(2x + 1)dx \Leftrightarrow \int {\frac{{d\left( {\sqrt {1 + {f^2}(x)} } \right)}}{{2\sqrt {1 + {f^2}(x)} }}} } \\\int {\left( {2x + 1} \right)dx \Leftrightarrow \sqrt {1 + {f^2}(x)}  = {x^2} + x + C} .\end{array}\]

Theo giả thiết f (0) = \[2\sqrt 2 \],

suy ra \[\int {\left( {2x + 1} \right)dx \Leftrightarrow \sqrt {1 + {{\left( {2\sqrt 2 } \right)}^2}}  = C}  \Leftrightarrow C = 3.\]

Với C = 3 thì

\[\begin{array}{l}\int {\left( {2x + 1} \right)dx \Leftrightarrow \sqrt {1 + {f^2}(x)}  = {x^2} + x + 3} \\ \Rightarrow f(x) = \sqrt {{{\left( {{x^2} + x + 3} \right)}^2} - 1} .\end{array}\]

Vậy f(1) = \[\sqrt {24} \].

Câu 43: Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 0 £ x £ 2020 và

log₃ (3x + 3) + x = 2y + 9^y ?

A. 2019 .

B. 6 .

C. 2020 .

D. 4 .

Lời giải

Điều kiện: x ³ 0 nên log₃ (3x + 3) xác định.

Ta có

log₃ (3x + 3) + x = 2y + 9^y

Û log₃ (x + 1) + (x + 1) = 2 log₃3^y + 9^y

Û log₃ (x + 1) + (x + 1) = log₃9^y + 9^y (1)

Xét hàm số f(t) = log₃t + t , t Î (0;+¥) có \[f'(t) = \frac{1}{{t\ln 3}} + 1 > 0,\forall t \in (0; + \infty ).\]

Do đó hàm số luôn đồng biến trên (0;+¥).

Khi đó (1) Û x = 9^y – 1

Vì 0 £ x £ 2020 nên 0 £ 9^y – 1 £ 2020 Û 0 £ y £ log₉ 2021.

Do y nguyên nên y Î {0;1;2;3} .

Þ (x;y) Î {(0;0);(8;1);(80;2);(728;3)}.

Vậy có 4 cặp số nguyên (x;y) thỏa mãn.

Nhận xét: Với dạng toán này việc quan trọng nhất là xác định được hàm đặc trưng f(t) = log₃ t + t, t Î (0;+¥). Ngoài ra, nếu để ý hàm số y = log₃ (3x + 3) + x đồng biến trên (-1; +¥), hàm số 2x + 9^x cũng đồng biến trên (-¥;+¥) nên 0 £ x £ 2020

Þ 1 £ 2y + 9^y £ log₃ 6063 + 2020 Þ - 1 £ y < 4.