Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tổng hợp bảng tóm tắt công thức Toán luyện thi THPT Quốc gia, tài liệu bao gồm 39 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tổng hợp bảng tóm tắt công thức Toán luyện thi THPT Quốc gia

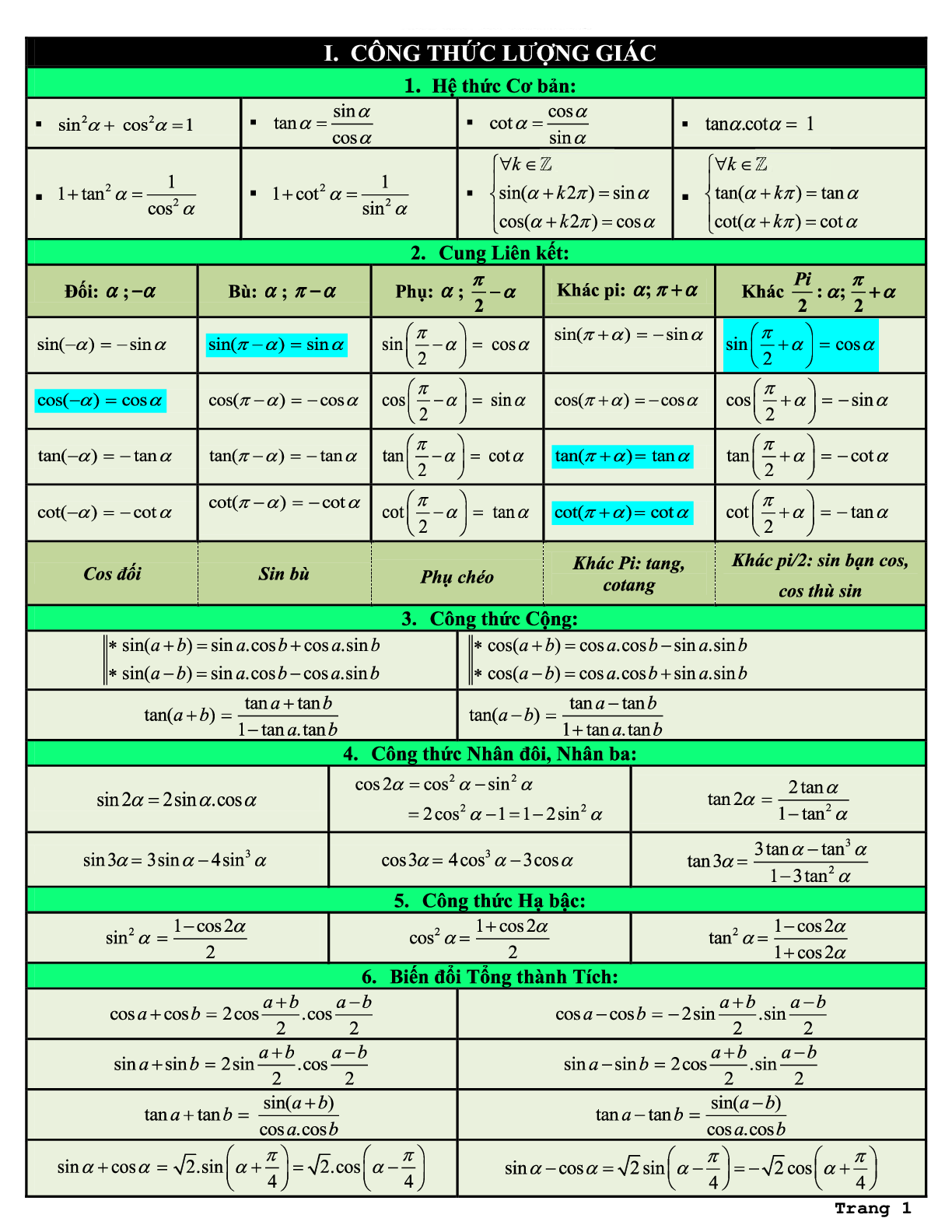
I. Công thức lượng giác

1.Hệ thức cơ bản

sin² α + cos² α = 1

tan α = \[\frac{{\sin \alpha }}{{{\rm{cos}}\alpha }}\]

cot α = \[\frac{{cos\alpha }}{{{\rm{sin}}\alpha }}\]

tan α.cot α = 1

1 + tan² α = \[\frac{1}{{co{s^2}\alpha }}\]

1 + cot² α = \[\frac{1}{{{{\sin }^2}\alpha }}\]

\[\left\{ {\begin{array}{*{20}{c}}{\forall k \in \mathbb{Z}}\\{\sin (\alpha  + k2\pi ) = \sin \alpha }\\{\cos (\alpha  + k2\pi ) = cos\alpha }\end{array}} \right.\]

\[\left\{ {\begin{array}{*{20}{c}}{\forall k \in \mathbb{Z}}\\{\tan (\alpha  + k\pi ) = \tan \alpha }\\{\cot (\alpha  + k\pi ) = \cot \alpha }\end{array}} \right.\]

2. Cung liên kết

Đối α; - α

Sin ( - α) = - sin α

Cos (- α) = cos α

Tan (- α) = - tan α

Cot (- α) = - cot α

Cos đối

Bù α; π – α

Sin (π – α) = sin α

Cos (π – α) = - cos α

Tan (π – α) = - tan α

Cot (π – α) = - cot α

Sin bù

Phụ α; \[\frac{\pi }{2} - \alpha \]

Sin (\[\frac{\pi }{2} - \alpha \]) = cos α

Cos (\[\frac{\pi }{2} - \alpha \]) = sin α

Tan (\[\frac{\pi }{2} - \alpha \]) = cot α

Cot (\[\frac{\pi }{2} - \alpha \]) = tan α

Phụ chéo

Khác pi α; π + α

Sin (π + α) = - sin α

Cos (π + α) = - cos α

Tan (π + α) = tan α

Cot (π + α) = cot α

Khác pi; tang; cotang

Khác \[\frac{\pi }{2}:\alpha ;\frac{\pi }{2} + \alpha \]

Sin (\[\frac{\pi }{2} + \alpha \]) = cos α

Cos (\[\frac{\pi }{2} + \alpha \]) = - sin α

Tan (\[\frac{\pi }{2} + \alpha \]) = - cot α

Cot (\[\frac{\pi }{2} + \alpha \]) = - tan α

Khác pi/2: sin bạn cos, cos thù sin

3. Công thức cộng:

sin (a + b) = sin a.cos b + cos a.sin b

sin (a - b) = sin a.cos b - cos a.sin b

cos (a + b) = cos a.cos b - sin a.sin b

cos (a - b) = cos a.cos b + sin a.sin b

tan (a + b) = \[\frac{{\tan a + \tan b}}{{1 - t{\rm{ana}}.\tan b}}\]

tan (a – b) = \[\frac{{\tan a - \tan b}}{{1 + t{\rm{ana}}.\tan b}}\]

4. Công thức Nhân đôi, nhân ba\

Sin 2α = 2 sin α.cos α

Sin 3α = 3sin α – 4sin³ α

Cos 2α = cos² α – sin² α = 2cos² α – 1 = 1 – 2sin² α

Cos 3α = 4 cos³ α – 3 cos α

Tan 2α = \[\frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }}\]

Tan 3α = \[\frac{{3\tan \alpha  - {{\tan }^3}\alpha }}{{1 - 3{{\tan }^2}\alpha }}\]

5. Công thức hạ bậc

sin² α = \[\frac{{1 - c{\rm{os2}}\alpha }}{2}\]

cos² α = \[\frac{{1 + c{\rm{os2}}\alpha }}{2}\]

tan² α = \[\frac{{1 - c{\rm{os2}}\alpha }}{{1 + c{\rm{os2}}\alpha }}\]

6. biến đổi Tổng thành Tích

Cos a + cos b = 2cos \[\frac{{a + b}}{{\rm{2}}}\].cos \[\frac{{a - b}}{{\rm{2}}}\]

Cos a - cos b = - 2sin \[\frac{{a + b}}{{\rm{2}}}\].sin \[\frac{{a - b}}{{\rm{2}}}\]

Sin a + sin b = 2sin \[\frac{{a + b}}{{\rm{2}}}\].cos \[\frac{{a - b}}{{\rm{2}}}\]

Sin a - sin b = 2cos \[\frac{{a + b}}{{\rm{2}}}\].sin \[\frac{{a - b}}{{\rm{2}}}\]

tan a + tan b = \[\frac{{\sin \left( {a + b} \right)}}{{{\rm{cosa}}{\rm{.cosb}}}}\]

tan a - tan b = \[\frac{{\sin \left( {a - b} \right)}}{{{\rm{cosa}}{\rm{.cosb}}}}\]

sin α + cos α = \[\sqrt 2 .\sin \left( {\alpha  + \frac{\pi }{4}} \right) = \sqrt 2 .c{\rm{os}}\left( {\alpha  - \frac{\pi }{4}} \right)\]

sin α - cos α = \[\sqrt 2 .\sin \left( {\alpha  - \frac{\pi }{4}} \right) =  - \sqrt 2 .c{\rm{os}}\left( {\alpha  + \frac{\pi }{4}} \right)\]

7. Công thức biến đổi tích thành tổng

Cos a. cos b = \[\frac{1}{2}\][cos(a + b) + cos(a – b)]

sin a. sin b = \[\frac{1}{2}\][cos(a - b) - cos(a + b)]

sin a. cos b = \[\frac{1}{2}\][sin(a + b) + sin(a – b)]

sin u = sin v \[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u = v + k2\pi }\\{u = \pi  - v + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\]

Nếu sin u = m \[ \in \][- 1;1] và m \[ \notin \left\{ { \pm 1; \pm \frac{{\sqrt 3 }}{2}; \pm \frac{{\sqrt 2 }}{2}; \pm \frac{1}{2};0} \right\}\] thì:

Sin u = m \[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u = \arcsin m + k2\pi }\\{u = \pi  - \arcsin m + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\]

Nếu sin u = m \[ \notin \][- 1;1] thì sin u = m ó u \[ \in \emptyset \]

Đặc biệt \[\left\langle {\begin{array}{*{20}{c}}{\sin u = 1 \Leftrightarrow u = \frac{\pi }{2} + k2\pi }\\{\sin u =  - 1 \Leftrightarrow u =  - \frac{\pi }{2} + k2\pi }\\{\sin u = 0 \Leftrightarrow u = k\pi }\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\]

Cos u = cos v \[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u = v + k2\pi }\\{u =  - v + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\]

Nếu cos u = m \[ \in \][- 1;1] và m \[ \ne \left\{ { \pm 1; \pm \frac{{\sqrt 3 }}{2}; \pm \frac{{\sqrt 2 }}{2}; \pm \frac{1}{2};0} \right\}\] thì:

Cos u = m ó u = \[ \pm \arcsin m + k2\pi \]\[\left( {k \in \mathbb{Z}} \right)\]

Nếu cos u = m \[ \notin \][- 1;1] thì cos u = m ó u \[ \in \emptyset \]

Đặc biệt \[\left\langle {\begin{array}{*{20}{c}}{\cos u = 1 \Leftrightarrow u = k2\pi }\\{\cos u =  - 1 \Leftrightarrow u =  - \pi  + k2\pi }\\{\cos u = 0 \Leftrightarrow u = \frac{\pi }{2} + k\pi }\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\]

Tan u = tan v ó u = v + k\[\pi \]\[\left( {k \in \mathbb{Z}} \right)\]

Nếu tan u = m\[ \notin \]\[\left\{ { \pm \sqrt 3 ; \pm 1; \pm \frac{{\sqrt 3 }}{3};0} \right\}\] thì

Tan u = m ó u = \[ \pm \arctan m + k\pi \]\[\left( {k \in \mathbb{Z}} \right)\]

Lưu ý: Điều kiện đển hàm tan u có nghĩa u \[ \ne \frac{\pi }{2} + k\pi \]\[\left( {k \in \mathbb{Z}} \right)\]. Tuy vậy, phương trình

tan u = m luôn có nghiệm, vì vậy không cần đặt điều kiện.

cot u = cot v ó u = v + k\[\pi \]\[\left( {k \in \mathbb{Z}} \right)\]

Nếu cot u = m\[ \notin \]\[\left\{ { \pm \sqrt 3 ; \pm 1; \pm \frac{{\sqrt 3 }}{3};0} \right\}\] thì

Cot u = m ó u = \[{\mathop{\rm arccot}\nolimits} m + k\pi \]\[\left( {k \in \mathbb{Z}} \right)\]

Lưu ý: Điều kiện đển hàm cot u có nghĩa u \[ \ne k\pi \]\[\left( {k \in \mathbb{Z}} \right)\]. Tuy vậy, phương trình

tan u = m luôn có nghiệm, vì vậy không cần đặt điều kiện.

cot u = cot v ó u = v + k\[\pi \]\[\left( {k \in \mathbb{Z}} \right)\]

Kỹ thuật 1: Làm mất dấu TRỪ

- sin α = Sin (– α)

- cos α = Cos (π – α) 

- tan α = tan (– α)

- cot α = cot ( – α)

Ví dụ:

\[\begin{array}{l}\sin \left( {x - \frac{\pi }{4}} \right) + {\mathop{\rm s}\nolimits} i{\rm{nx}} = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) =  - {\mathop{\rm s}\nolimits} i{\rm{nx}} \Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) = \sin ( - x)\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{\pi }{4} =  - x + k2\pi }\\{x - \frac{\pi }{4} = \pi  + x + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{8} + k\pi (k \in \mathbb{Z}).\end{array}\]

Kỹ thuật 2: Biến đổi CHÉO

sin α = cos (\[\frac{\pi }{2} - \alpha \])

cos α = sin (\[\frac{\pi }{2} - \alpha \])

tan α = cot (\[\frac{\pi }{2} - \alpha \])

cot α = tan (\[\frac{\pi }{2} - \alpha \])

Ví dụ

Sin 2x = cos x ó sin 2x = \[\sin \left( {\frac{\pi }{2} - x} \right)\]

\[\begin{array}{l} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \frac{\pi }{2} + k2\pi }\\{2x = \pi  - \left( {\frac{\pi }{2} - x} \right) + k2\pi }\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + \frac{{k2\pi }}{3}}\\{x = \frac{\pi }{2} + k2\pi }\end{array}} \right.\left( {k \in \mathbb{Z}} \right).\end{array}\]

Phương trình asinx + bcosx = c (với a² + b² \[ \ge \]c²)

asinx + bcosx = c

 \[\begin{array}{l} \Leftrightarrow \frac{a}{{\sqrt {{a^2} + {b^2}} }}\sin x + \frac{b}{{\sqrt {{a^2} + {b^2}} }}{\rm{cosx = }}\frac{c}{{\sqrt {{a^2} + {b^2}} }}\\ \Leftrightarrow \sin x.c{\rm{os}}\alpha {\rm{ + }}c{\rm{osx}}{\rm{.sin}}\alpha  = \frac{c}{{\sqrt {{a^2} + {b^2}} }}\end{array}\]

(với \[{\rm{cos}}\alpha {\rm{ = }}\frac{a}{{\sqrt {{a^2} + {b^2}} }}{\rm{sin}}\alpha {\rm{ = }}\frac{b}{{\sqrt {{a^2} + {b^2}} }}\])

\[ \Leftrightarrow \sin \left( {x + \alpha } \right){\rm{ = sin}}\beta  \Leftrightarrow ...\] với \[{\rm{sin}}\beta  = \frac{c}{{\sqrt {{a^2} + {b^2}} }}\]

Phương trình asin² x + bsinx cosx + c cos²x = d

Trường hợp 1: Xét cos x = 0 \[ \Rightarrow \] sin² x = 1. Ta có hệ sau

\[\left\{ {\begin{array}{*{20}{c}}{{{\sin }^2}x = 1}\\{a{{\sin }^2}x = d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\sin }^2}x = 1}\\{a = d}\end{array}} \right. \Leftrightarrow .....(1)\]

Trường hợp 2: Xét cos x \[ \ne \] 0, chia hai vế phương trình cho cos²x, ta có:

a tan²x +b tan x + c = d(1 + tan² x) \[ \Leftrightarrow ....(2)\]

Hợp nghiệm của (1), (2) ta có nghiệm của phương trình đã cho.

Lưu ý: Phương trình asin x + bcos x = c chỉ có nghiệm khi và chỉ khi a² + b² \[ \ge \] c².

III. Tổ hợp – Xác suất

Quy tắc cộng

Nếu phép đếm được chia ra nhiều trường hợp, ta sẽ cộng các kết quả lại.

Quy tắc nhân

Nếu phép đếm được chia ra làm nhiều giai đoạn bắt buộc, ta sẽ nhân các kết quả của mỗi giai đoạn ấy.

Hoán vị

Sắp xếp (đổi chỗ) của n phần tử khác nhau, ta có số cách xếp P_n = n! với n \[ \in \mathbb{N}\]

n! = 1.2….(n – 1)n.

Quy ước số: 0! = 1.

Tổ hợp

Chọn k phần tử từ n phần tử (không sắp xếp thứ tự), ta có số cách chọn là \[C_n^k\].

\[C_n^k = \frac{{n!}}{{(n - k)!k!}}\] với \[\left\{ {\begin{array}{*{20}{c}}{k \in \mathbb{N},n \in \mathbb{N}*}\\{0 \le k \le n}\end{array}} \right.\]

Chỉnh hợp

Chọn k phần tử từ n phần tử (có sắp xếp thứ tự), ta được số cách chọn là \[A_n^k\].

\[A_n^k = \frac{{n!}}{{(n - k)!}}\] với \[\left\{ {\begin{array}{*{20}{c}}{k \in \mathbb{N},n \in \mathbb{N}*}\\{0 \le k \le n}\end{array}} \right.\]

Một số tính chất

\[C_n^k = C_n^{n - k}\]

\[C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1}\]

\[A_n^k = k!C_n^k\]

Xác suất

Công thức P(X) = \[\frac{{n(X)}}{{n(\Omega )}}\]

Trong đó: n(X) : số phần tử của tập biến cố X; \[n(\Omega )\]: số phần tử không gian mẫu; P(X) là xác suất của biến cố để biến cố X xảy ra với \[X \subset \Omega \].

Nếu A, B là hai biến cố xung khác với nhau thì

\[P(A \cup B) = P(A) + P(B).\]

Nếu A, B là hai biến cố độc lập với nhau thì \[P(A.B) = P(A).P(B).\]

Tính chất

\[\begin{array}{l}0 \le P(X) \le 1\\P(\emptyset ) = 0;P(\Omega ) = 1\end{array}\]

\[P(X) = 1 - P(\overline X )\] với \[\overline X \] là biến cố đối của X.

IV. Khai triển nhị thức Newton

Khai triển dạng liệt kê: ( với \[n \in \mathbb{N}*\])

(a + b)ⁿ = \[C_n^0{a^n} + C_n^1{a^{n - 1}}b + C_n^2{a^{n - 2}}{b^2} + ...C_n^{n - 1}a{b^{n - 1}} + C_n^n{b^n}\].

Đặc biệt: \[{(1 + x)^n} = C_n^0 + C_n^1x + C_n^2x + ...C_n^{n - 1}{x^{n - 1}} + C_n^n{x^n}\]     (*).

Hệ quả 1: \[C_n^0 + C_n^1 + C_n^2 + ...C_n^{n - 1} + C_n^n = {2^n}\] (tức thay x = 1 vào (*)).

Hệ quả 2: Với n chẵn, chỉ cần thay x = - 1 vào (*), ta có:

\[\begin{array}{l}C_n^0 - C_n^1 + C_n^2 - ... - C_n^{n - 1} + C_n^n = 0\\ \Leftrightarrow C_n^0 + C_n^2 + C_n^4... + C_n^n = C_n^1 + C_n^3 + ...C_n^{n - 1}\end{array}\]

Khai triển dạng tổng quát: ( với \[n \in \mathbb{N}*\])

Khai triển: \[{(a + b)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \]

Số hạng tổng quát: \[{T_{k + 1}} = C_n^k{a^{n - k}}{b^k}\]

Phận biệt hệ số và số hạng \[{T_{k + 1}} = \underbrace {\underbrace {C_n^k{{\left( { - 1} \right)}^k}{a^{n - k}}{b^k}}_{heso}.{x^\alpha }}_{sohang}\]. Số hạng không chứa x ứng với \[\alpha  = 0\].

V. Cấp số cộng – Cấp số nhân

Cấp số cộng

1, Định nghĩa

Dãy số (u_n) được gọi là cấp số cộng khi và chỉ khi u_n+1 = u_n + d với \[n \in \mathbb{N}*\], d là hằng số.

Cấp số cộng như trên có số hạng đầu u₁, công sai d.

2, Số hạng tổng quát

u_n = u₁ +(n – 1)d với \[k \in \mathbb{N}*\]

3, Tính chất các số hạng:

u_k-1 + u_k+1 = 2u_k với \[k \in \mathbb{N}*\] và \[k \ge 2\]

4. Tổng n số hạng đầu tiên

S_n = u₁ + u₂ + … + u_n = \[\frac{{\left( {{u_1} + {u_n}} \right)n}}{2}.\]

Cấp số nhân

1, Định nghĩa

Dãy số (u_n) được gọi là cấp số cộng khi và chỉ khi u_n+1 = u_n.q với \[n \in \mathbb{N}*\], q là hằng số.

Cấp số cộng như trên có số hạng đầu u₁, công bội q.

2, Số hạng tổng quát

u_n = u_1.q^n-1  với \[n \in \mathbb{N}*\]

3, Tính chất các số hạng:

u_k-1 . u_k+1 = u_k² với \[k \in \mathbb{N}\] và \[k \ge 2\]

4. Tổng n số hạng đầu tiên

S_n = u₁ + u₂ + … + u_n = \[\frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\] với q ≠ 1.

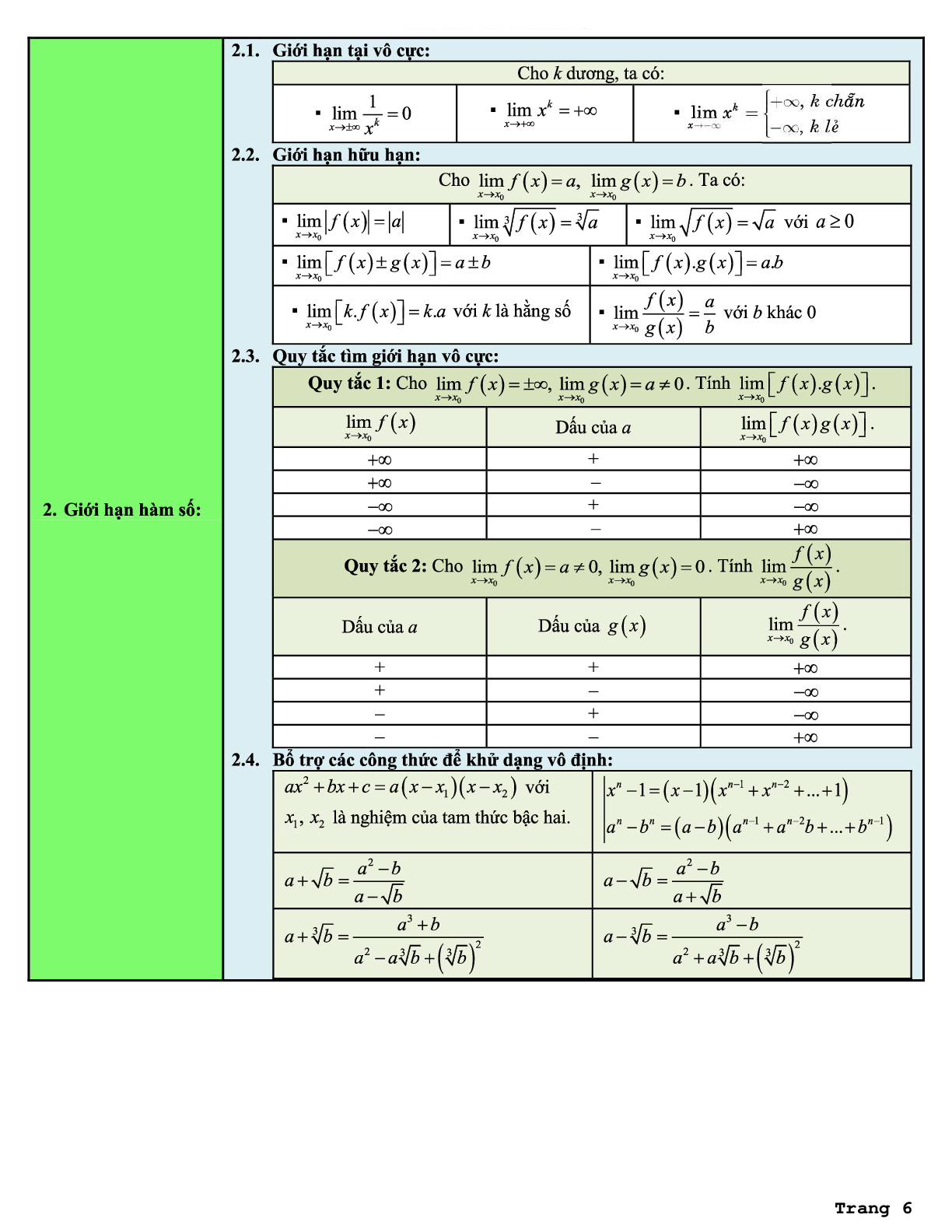
VI. Giới hạn dãy số - Hàm số

1.1 Dãy số có giới hạn 0:

\[\lim \frac{1}{n} = 0;\lim \frac{1}{{\sqrt n }} = 0;\lim \frac{1}{{\sqrt[3]{n}}} = 0;\lim \frac{1}{{{n^\alpha }}} = 0\]

\[\lim {q^n} = 0\] với \[\left| q \right| < 1\]

1.2 Dãy số có giới hạn hữu hạn:

Cho lim u_n = a. Ta có:

\[\lim \left| {{u_n}} \right| = \left| a \right|\] và \[\lim \sqrt[3]{u} = \sqrt[3]{a}\]

\[\lim \sqrt {{u_n}}  = \sqrt a \] với \[a \ge 0\].

Cho lim u_n = a, lim v_n = b. Ta có:

\[\begin{array}{l}\lim \left( {u \pm v} \right) = a \pm b\\\lim \left( {{u_n}.{v_n}} \right) = a.b\\\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b},b \ne 0\\\lim \left( {k.{u_n}} \right) = k.a\end{array}\]

1.3 Tổng của chấp số nhân lùi vô hạn

S = u₁ + u₁q + u₁q² + … = \[\frac{{{u_1}}}{{1 - q}}\].

1.4 Dãy số có giới hạn vô cùng:

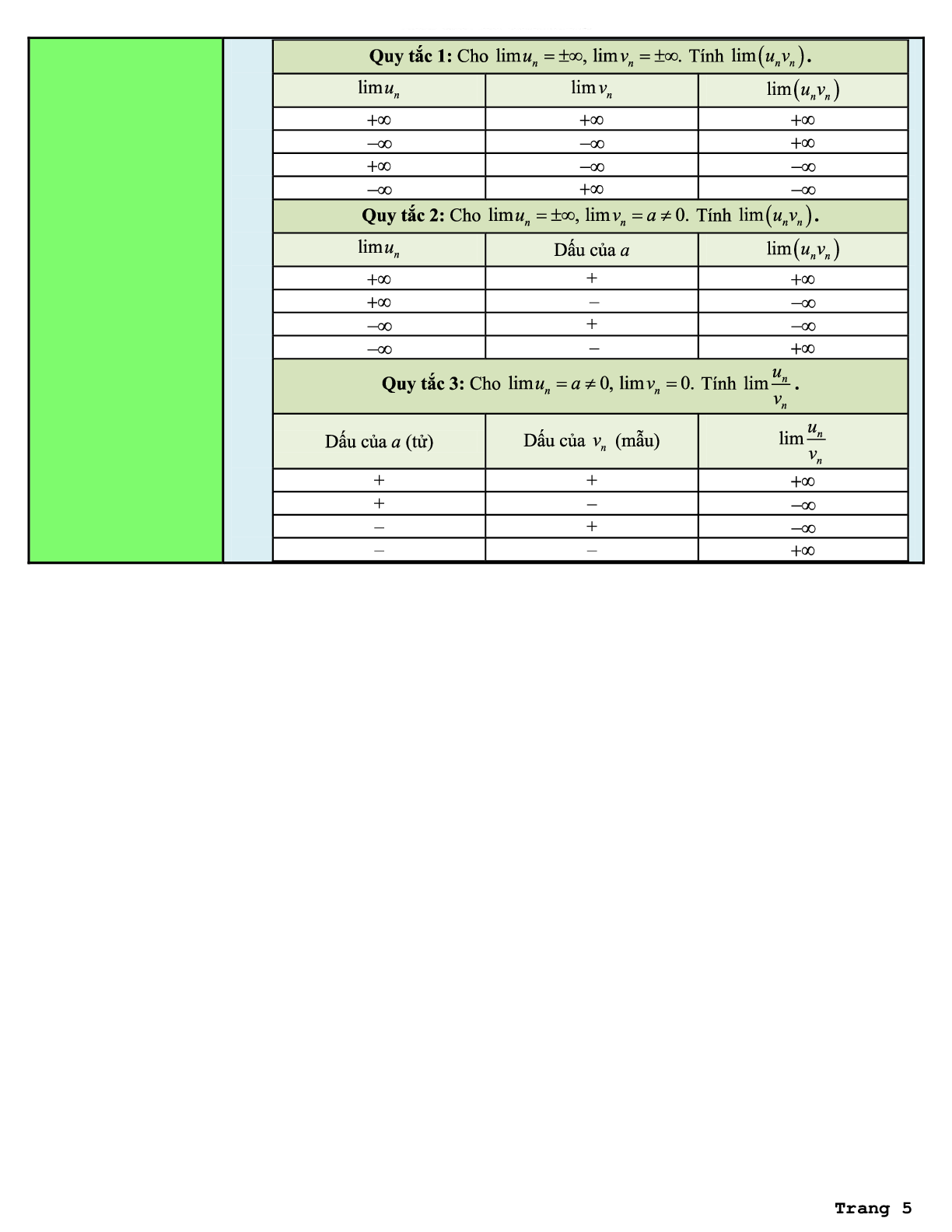
Quy tắc 1: Cho lim u_n = \[ \pm \infty \], lim v_n = \[ \pm \infty \]. Tính lim (u_n.v_n).

Quy tắc 2: Cho lim u_n = \[ \pm \infty \], lim v_n = a ≠ 0. Tính lim (u_n.v_n).

Quy tắc 3: Cho lim u_n = a ≠ 0, lim v_n = 0. Tính lim \[\frac{{{u_n}}}{{{v_n}}}\].