Tailieumoi.vn xin giới thiệu Bài tập Toán 12 Chương 4 Bài 4:Phương trình bậc hai với hệ số thực. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 4: Phương trình bậc hai với hệ số thực. Mời các bạn đón xem:
Bài tập Toán 12 Chương 4 Bài 4: Phương trình bậc hai với hệ số thực
A. Bài tập Phương trình bậc hai với hệ số thực
I. Bài tập trắc nghiệm
Bài 1: Phương trình z2 + 4x + 5 = 0 có các nghiệm là
A. 2 ± i
B. -2 ± i
C. 4 ± i
D. -4 ± i
Lời giải:
Ta có: Δ' = 22 - 1.5 = -1 = i2. Phương trình có hai nghiệm là:
Bài 2: Phương trình z2 + 8z + 17 = 0 có hai nghiệm
A. 1 - i và 1 - 2i
B. 4 - i và 4 + i
C. -4 - i và -4 + i
D. -2 + 2i và -2 + 4i
Lời giải:
Ta có: Δ = 16 - 17 = -1 = i2. Phương trình có các nghiệm là:
z1 = -4 - i, z2 = -4 + i
Bài 3: Phương trình z2 - 4z + 9 = 0 có hai nghiệm. Giá trị biểu thức T = |z1| + |z2| bằng
A. – 6
B. 6
C. 8
D. 2
Lời giải:
Ta có: Δ' = 4 - 9 = -5 = 5i2. Phương trình có hai nghiệm là:
z1,2 = 2 ± i
Vậy T = 2 = 2 = 6
Bài 4: Phương trình z4 + 3z2 - 4 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1| + |z2| + |z3| + |z4| bằng
A. 6
B. 2
C. 2 + 2
D. 4 + 2
Lời giải:
Ta có
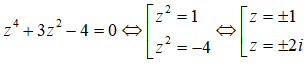
⇒ |z1| = |z2| = 1; |z3| = |z4| = 2
Vậy T = 1 + 1 + 2 + 2 = 6
Bài 5: Số phức z thỏa mãn
Giá trị biểu thức
A. 1
B. 2
C. 3
D. 3672
Lời giải:
Ta có: z + = <=> z2 - z + 1 = 0 (1)
Xét phương trình (1): Ta có: Δ = ()2 - 4.1.1 = -1 = i2
Phương trình (1) có hai nghiệm là:
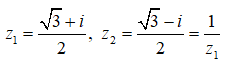
Do đó
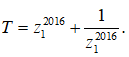
Ta có:
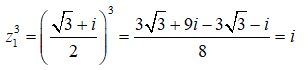
Vậy T = 1 + 1 = 2
Bài 6: Phương trình z2 -az + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi
A. a = 2, b = -2
B. a = 2, b = 2
C. a = -2, b = 2
D. a = -2, b = -2
Lời giải:
Thay z = 1 + i vào phương trình đã cho ta có:
Chọn đáp án B.
Bài 7: Phương trình 2z2 + 4z + 5 = 0 có các nghiệm là
Lời giải:
Ta có: Δ' = 4 - 10 = -6 = 6i2
Phương trình đã cho có các nghiệm là
Chọn đáp án C.
Bài 8: Phương trình z2 - z + 1 = 0 có hai nghiệm là
Lời giải:
Ta có: Δ = 12 - 4 = -3 = 3i2
Các nghiệm của phương trình đã cho là
Chọn đáp án A.
Bài 9: Để phương trình z2 + bz + c = 0 nhận z1 = -4 + 2i và z2 = -4 - 2i làm nghiệm thì
A. b = -8, c = 20
B. b = -8, c = -20
C. b = 8, c = 20
D. b = 8, c = 20
Lời giải:
Gọi z1, z2 là hai nghiệm của phương trình đã cho, áp dụng hệ thức Vi-ét ta có:
Để phương trình đã cho nhận z1, z2 làm nghiệm thì
Chọn đáp án D.
Bài 10: Phương trình z2 + 6z + 15 = 0 có các nghiệm là z1, z2. Giá trị biểu thức T = |z1| + |z2| bằng:
A. 2
B. 6
C. 4
D. 2
Lời giải:
Ta có:Δ' = 9 - 15 = -6 = 6i2
Các nghiệm của phương trình là z1 = - 3 - i, z2 = - 3 + i
Do đó
Chọn đáp án A.
II. Bài tập tự luận có lời giải
Bài 1: Phương trình z1 = 1 + 2i, z2 = 2 - 3i có nghiệm là z = 2 + i khi
A. a = 1, b = 4
B. a = -1, b = 4
C. a = -1, b = -4
D. a = 1, b = -4
Lời giải:
Thay z = 2 + i vào phương trình đã cho ta có:
Bài 2: Phương trình (1 + i)2 = -7 + i có các nghiệm là?
Lời giải:
Phương trình đã cho tương đương với
Viết -3 + 4i = 4i2 + 4i + 1 = (2i + 1)2, ta có: z2 = (2i + 1)2 <=> z = ±(2i + 1)
Chú ý: Nếu việc viết -3 + 4i = (2i + 1)2 gặp khó khăn thì có thể đặt z = a + bi (a, b ∈ R). Ta có :
(a + bi)2 = -3 + 4i <=> a2 - b2 + 2abi = -3 + 4i
Từ phương trình thứ hai của hệ ta có b =
Thay vào phương trình thứ nhất của hệ ta có
Vì a ∈ R và a2 ≥ 0 nên a2 = 1 hay a = ±1. Từ đó ta có hai nghiệm : z1 = -1 - 2i và z2 = 1 + 2i
Câu 3: Phương trình z2 -az + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi
Lời giải:
Thay z = 1 + i vào phương trình đã cho ta có:
Câu 4: Phương trình 2z2 + 4z + 5 = 0 có các nghiệm là?
Lời giải:
Ta có: Δ' = 4 - 10 = -6 = 6i2
Phương trình đã cho có các nghiệm là
Chọn đáp án C.
Câu 5: Phương trình z2 - z + 1 = 0 có hai nghiệm là?
Lời giải:
Ta có: Δ = 12 - 4 = -3 = 3i2
Các nghiệm của phương trình đã cho là
Câu 6: Để phương trình z2 + bz + c = 0 nhận z1 = -4 + 2i và z2 = -4 - 2i làm nghiệm thì?
Lời giải:
Gọi z1, z2 là hai nghiệm của phương trình đã cho, áp dụng hệ thức Vi-ét ta có:
Để phương trình đã cho nhận z1, z2 làm nghiệm thì
Câu 7: Phương trình z2 + 6z + 15 = 0 có các nghiệm là z1, z2.Giá trị biểu thức T = |z1| + |z2| bằng?
Lời giải:
Ta có:Δ' = 9 - 15 = -6 = 6i2
Các nghiệm của phương trình là z1 = - 3 - i, z2 = - 3 + i
Do đó
Câu 8: Phương trình z1 = 1 + 2i, z2 = 2 - 3i có nghiệm là z = 2 + i khi
Lời giải:
Thay z = 2 + i vào phương trình đã cho ta có:
Câu 9: Phương trình (1 + i)2 = -7 + i có các nghiệm là
Lời giải:
Phương trình đã cho tương đương với
Viết -3 + 4i = 4i2 + 4i + 1 = (2i + 1)2, ta có: z2 = (2i + 1)2 <=> z = ±(2i + 1)
Chú ý: Nếu việc viết -3 + 4i = (2i + 1)2 gặp khó khăn thì có thể đặt z = a + bi (a, b ∈ R). Ta có :
(a + bi)2 = -3 + 4i <=> a2 - b2 + 2abi = -3 + 4i
Từ phương trình thứ hai của hệ ta có b =
Thay vào phương trình thứ nhất của hệ ta có
Vì a ∈ R và a2 ≥ 0 nên a2 = 1 hay a = ±1 . Từ đó ta có hai nghiệm : z1 = -1 - 2i và z2 = 1 + 2i
Câu 10: Phương trình z2 + 4x + 5 = 0 có các nghiệm là
Lời giải:
Ta có: Δ' = 22 - 1.5 = -1 = i2. Phương trình có hai nghiệm là:
III. Bài tập vận dụng
Bài 1 Phương trình z2 + 8z + 17 = 0 có hai nghiệm là?
Bài 2 Phương trình z2 - 4z + 9 = 0 có hai nghiệm. Giá trị biểu thức T = |z1| + |z2| bằng?
Bài 3 Phương trình z4 + 3z2 - 4 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1| + |z2| + |z3| + |z4| bằng?
Bài 4 Thế nào là căn bậc hai của số thực dương a ?
Bài 5 Tìm các căn bậc hai phức của các số sau: -7;-8;-12;-20;-121
Bài 6 Giải các phương trình sau trên tập hợp số phức:
a) -3z2 + 2z - 1 = 0
b) 7z2 + 3z + 2 = 0
c) 5z2 - 7z + 11 = 0
Bài 7 Giải các phương trình sau trên tập hợp số phức:
a) z4 + z2 - 6 = 0
b) z4 + 7z2 + 10 = 0
Bài 8 Cho a, b, c ∈R,a ≠ 0,z1 , z2 là hai nghiệm phân biệt ( thực hoặc phức) của phương trình ax2+bx+c=0. Hãy tính z1+z2 và z1.z2 theo hệ số a, b, c.
Bài 9 Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và z− làm nghiệm.
Bài 10 Tìm các căn bậc hai của w = -5 + 12i.
B. Lý thuyết Phương trình bậc hai với hệ số thực
1. Căn bậc hai của số thực âm
Tương tự căn bậc hai của một số thực dương, từ i2 = –1, ta nói i là một căn bậc hai của – 1; – i cũng là một căn bậc hai của –1 vì (–i)2 = –1.
Từ đó, ta xác định được căn bậc hai của các số thực âm, chẳng hạn.
Căn bậc hai của –16 là vì
Căn bậc hai của –5 là vì
Tổng quát, các căn bậc hai của số thực a âm là .
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai ax2 + bx + c = 0 với a; b ; c.
Xét biệt số ∆ = b2 – 4ac của phương trình. Ta thấy:
Khi ∆ = 0, phương trình có một nghiệm thực .
Khi ∆ > 0, có hai căn bậc hai thực của ∆ là và phương trình có hai nghiệm thực phân biệt, được xác định bởi công thức .
Khi ∆ < 0, ta có hai căn bậc hai thuần ảo của ∆ là . Khi đó, phương trình có hai nghiệm phức được xác định bởi công thức .
– Nhận xét:
Trên tập hợp số phức, mọi phương trình bậc hai đều có hai nghiệm (không nhất thiết phân biệt).
Tổng quát: Mọi phương trình bậc n :
a0.xn + a1.xn – 1 + ….+ an–1.x + an = 0
Trong đó; a0 ; a1;…..; anđều có n nghiệm phức (các nghiệm không nhất thiết phân biệt).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
