Tailieumoi.vn xin giới thiệu Bài tập Toán 11 Chương 3 Bài 1: Vectơ trong không gian. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 1: Vectơ trong không gian. Mời các bạn đón xem:
Bài tập Toán 11 Chương 3 Bài 1: Vectơ trong không gian
A. Bài tập Vectơ trong không gian.
I. Bài tập trắc nghiệm
Bài 1: Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
a) Vecto bằng:
A.
B.
C.
D.
b) Vecto bằng:
A.
B.
C.
D.
Đáp án: a - B, b - D
a.
b.
Bài 2: Cho tứ diện ABCD và . Gọi M, N, P và Q lần lượt là trung điểm của AB, BC, CD, và DA.
a) Vecto bằng:
A.
B.
C.
D.
b) Vecto bằng:
A.
B.
C.
D.
c) Bốn điểm M, N, P, Q cùng thuộc mặt phẳng vì:
A.
B.
C.
D.
Đáp án: a - A, b - C, c - D
a. MQ=1
b.Loại ngay hai phương án A và B vì không đồng phẳng có vecto và . Phương án đúng là C vì
c. Phương án A loại vì đẳng thức () đúng nhưng chưa chứng tỏ được bốn điểm M, N, P, Q đồng phẳng.
Phương án B loại vì đẳng thức. sai
Phương án C loại vì đẳng thức đúng nhưng không liên quan đến hai điểm N và Q.
Phương án D đúng vì đẳng thức đúng và chứng tỏ ba vecto đồng phẳng.
Bài 3: Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh bằng a.
a) Số đo góc giữa và bằng:
A. 300
B. 600
C. 900
D. 1200
b) Gọi M là điểm bất kì trên AC. Góc giữa và bằng 900 khi M:
A. Trùng với A
B. Trùng với C
C. Là trung điểm của AC
D. Bất kì vị trí nào trên AC.
Đáp án: a - B, b - C
Bài 4: Cho tứ diện ABCD, E và F lần lượt là trung điểm của AB và CD, AB = 2a, CD = 2b và EF = 2c. M là một điểm bất kì.
a) MA2 + MB2 bằng:
A. 2ME2 + 2a2
B. 2MF2 + 2a2
C. 2ME2 + 2b2
D. 2MF2 + 2b2
b) MC2 + MD2 bằng:
A. 2ME2 + 2a2
B. 2MF2 + 2a2
C. 2ME2 + 2b2
D. 2MF2 + 2b2
c) Gọi G là trọng tâm của tứ diện ABCD. ME2 + MF2 bằng:
A. 2MG2 + 2a2
B. 2MG2 + 2b2
C. 2MG2 + 2c2
D. 2MG2 + 2(a2 + b2 + c2)
d) MA2 + MB2 + MC2 + MD2 bằng:
A. 4MG2 + 2a2
B. 4MG2 + 2b2
C. 4MG2 + 2c2
D. 4MG2 + 2(a2 + b2 + c2)
Đáp án: a - A, b - D, c - C
a. MA2 = ()2 = ME2 + EA2 + 2.
MB2 = ()2 = ME2 + EB2 + 2
Suy ra: MA2 + MB2 = 2ME2 + 2a2 (do )
b. Tương tự MC2 + MD2 = 2MF2 + 2b2
c. Tương tự ME2 + MF2 = 2MG2 + 2c2
d. MA2 + MB2 + MC2 + MD2 = 2ME2 + 2MF2 + 2a2 + 2b2 = 4MG2 + 2(a2 + b2 + c2)
Bài 5: Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là l. Gọi M là trung điểm của các cạnh AB. Góc giữa hai vecto và bằng:
A. 00
B. 450
C. 900
D. 1200
Đáp án: D
Bài 6: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC bằng .
a) Tích vô hướng bằng:
b) Tích vô hướng bằng:
c) Góc giữa hai đường thẳng AB và SC bằng:
A. 00
B. 1200
C. 600
D. 900
Đáp án: a - C, b - D, c - C
Phương án A sai vì ≠ ||.|| = a2
Phương án B sai vì:
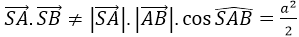
Phương án C đúng:
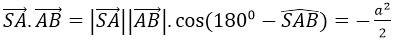
Phương án D sai vì ≠ -| |.| | = -a2
Tam giác SAC; SAB là tam giác đều
tam giác SCB; ABC vuông cân.
Bài 7: Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho và , với m khác 1. Vecto bằng:
A.
B.
C.
D.
Đáp án: C
Phần dẫn ví dụ 1 là một câu chưa hoàn chỉnh, người làm chắc nghiệm phải lựa chọn một trong bốn phương án đưa ra để được một khẳng định đúng.
Có thể loại các phương án A, B và D vì các cặp ba vecto
(), () và () đều không đồng phẳng.
Phương án C đúng vì :
Bài 8: Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
a) Vecto cùng với hai vecto nào sau đây là ba vecto đồng phẳng?
A. và
B. và
C. và
D. và
b) Vecto cùng với hai vecto nào sau đây là ba vecto không đồng phẳng?
A. và
B. và
C. và
D. và
Đáp án: a - C, b - A
a) Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
Suy ra: MN// AC và (1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành ( có các cạnh đối song song và bằng nhau
⇒ (3)
Lại có: = (4)
Từ (3); (4) ⇒
Do đó, 3 vecto đồng phẳng
b) Phương án A là đúng.
B sai vì nên 3 vecto đồng phẳng
C sai vì nên 3 vecto đồng phẳng
D sai vì nên 3 vecto đồng phẳng
Bài 9: Cho ba vecto . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
A. Một trong ba vecto đó bằng
B. Có hai trong ba vecto đó cùng phương.
C. Có một vecto không cùng hướng với hai vecto còn lại
D. Có hai trong ba vecto đó cùng hướng.
Đáp án: C
Nếu hai trong ba vecto đó cùng hướng thì ba vecto đồng phẳng; nếu hai trong ba vecto đó không cùng hướng thì chưa thể kết luận được ba vecto đó đồng phẳng.
Bài 10: Ba vecto không đồng phẳng nếu?
A. Ba đường thẳng chứa chúng không cùng một mặt phẳng.
B. Ba đường thẳng chứa chúng cùng thuộc một mặt phẳng.
C. Ba đường thẳng chứa chúng không cùng song song với một mặt phẳng.
D. Ba đường thẳng chứa chúng cùng song song với một mặt phẳng.
Đáp án: C
Bài 11 Cho hình chóp S.ABC, có SA ⊥ (ABC). Góc giữa đường thẳng SC và mặt đáy là góc nào dưới đây?
A. ;
B. ;
C. ;
D. .
II. Bài tập tự luận có lời giải
Bài 1: Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
a) Những vecto khác bằng nhau là:
b) bằng:
A. 4
B. 2
C.
D.
a.;
b.
Bài 2 Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB', CC', DD' lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:
Lời giải:
Lời giải:
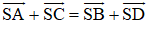
Lời giải:
Lời giải:
Lời giải:
a) Lấy điểm G sao cho
⇒ G là đỉnh còn lại của hình bình hành ABGC.
Khi đó
⇒ E là đỉnh còn lại của hình bình hành AGED.
Hay E là đường chéo của hình hộp có ba cạnh lần lượt là AB; AC; AD.
⇒ F là đỉnh còn lại của hình bình hành ADGF
Hay F là điểm đối xứng với E qua G.
Bài 8 Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. CMR:
Lời giải
Lời giải:
Lời giải:
Lời giải:
Do đó, ba vecto đồng phẳng
Bài 12 Cho hình chóp S.ABC, có SA ⊥ (ABC), SA = a, AB = a . Tính số đo góc giữa đường thẳng SB và mặt phẳng (ABC).
Lời giải:
Ta có: SB ∩ (ABC) tại B.
S ∈ SB và hình chiếu vuông góc của S lên (ABC) là A (vì SA ⊥ (ABC))
Do đó, góc giữa đường thẳng SB và mặt phẳng (ABC) là .
Xét tam giác SAB vuông tại A có:
.
Vậy góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 30°.
Bài 13 Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Góc giữa đường thẳng SA và mặt phẳng (ABCD) là bao nhiêu?
Lời giải:
Gọi O là giao điểm của AC và BD.
Vì S.ABCD là hình chóp tứ giác đều nên ta có SO ⊥ (ABCD).
SA ∩ (ABCD) = A và O là hình chiếu vuông góc của S lên (ABCD) nên:
Góc giữa đường thẳng SA và mặt phẳng (ABCD) là .
Ta có:
Khi đó,
Vậy góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.
III. Bài tập vận dụng
Bài 1
Bài 2 Cho hình lăng trụ tứ giác: . Mặt phẳng cắt các cạnh bên lần lượt tại . Xét các vectơ có các điểm đầu là các điểm và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:
a) Các vectơ cùng phương với ;
b) Các vectơ cùng hướng với ;
c) Các vectơ ngược hướng với .
Bài 3 Cho hình hộp . Chứng minh rằng:
a) + + = ;
b) - - = ;
c) + + + = .
Bài 4 Cho hình bình hành . Gọi là một điểm nằm ngoài mặt phẳng chứa hình bình hành. chứng minh rằng:
Bài 5 Cho hình tứ diện . Gọi và lần lượt là trung điểm của và . Chứng minh rằng:
a)
b)
Bài 6 Cho hình tứ diện . Hãy xác định hai điểm sao cho:
a)
b)
Bài 7 Cho hình tứ diện . Gọi là trọng tâm tam giác . Chứng minh rằng:
Bài 8 Gọi và lần lượt là trung điểm của các cạnh và của tứ diện . Gọi là trung điểm của đoạn thẳng và là một điểm bất kì trong không gian. Chứng minh rằng:
a)
b)
Bài 9 Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’.
Bài 10 Cho tứ diện ABCD. Gọi M, N, P và Q lần lượt là trung điểm của AB, BC, CD, và DA.
B. Lý thuyết Vectơ trong không gian.
I. Định nghĩa và các phép toán về vecto trong không gian.
Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B ta có một vecto, được kí hiệu là .
1. Định nghĩa.
- Vecto trong không gian là một đoạn thẳng có hướng. Kí hiệu chỉ vecto có điểm đầu là A, điểm cuối là B. Vecto còn được kí hiệu là
- Các khái niệm liên quan đến vecto như giá của vecto, độ dài của vecto, sự cùng phương, cùng hướng của vecto, vecto – không, sự bằng nhau của hai vecto … được định nghĩa tương tự như trong mặt phẳng.
2. Phép cộng và phép trừ vecto trong không gian
- Phép cộng và phép trừ của hai vecto trong không gian được định nghĩa tương tự như phép cộng và phép trừ hai vecto trong mặt phẳng.
- Phép cộng vecto trong không gian cũng có các tính chất như phép cộng vecto trong mặt phẳng. Khi thực hiện phép cộng vecto trong không gian ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vecto trong hình học không gian.
Ví dụ 1. Cho tứ diện ABCD. Chứng minh
Lời giải:
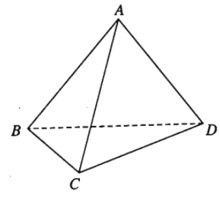
Áp dụng quy tắc ba điểm ta có:
Ta có:
( điều phải chứng minh).
II. Điều kiện đồng phẳng của ba vecto.
1. Khái niệm về sự đồng phẳng của ba vecto trong không gian.
Trong không gian cho ba vecto . Nếu từ một điểm O bất kì ta vẽ: thì có thể xảy ra hai trường hợp:
+ Trường hợp các đường thẳng OA; OB; OC không cùng nằm trong một mặt phẳng, khi đó ta nói rằng ba vecto không đồng phẳng.
+ Trường hợp các đường thẳng OA; OB; OC cùng nằm trong một mặt phẳng thì ta nói rằng ba vecto đồng phẳng.
Trong trường hợp này, giá của các vecto luôn luôn song song với một mặt phẳng.
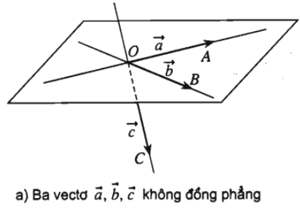
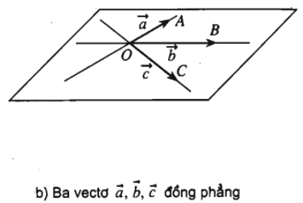
- Chú ý. Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vecto nói trên không phụ thuộc vào việc chọn điểm O.
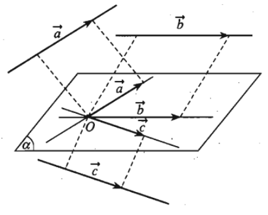
2. Định nghĩa:
Trong không gian ba vecto được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
Ví dụ 2. Cho hình hộp ABCD.EFGH. Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Chứng minh đồng phẳng.
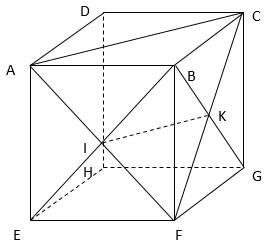
Lời giải:
Xét tam giác FAC có I ; K lần lượt là trung điểm của AF và FC nên IK là đường trung bình của tam giác.
IK// AC nên IK// mp ( ABCD) .
Vì BC// GF nên GF // mp( ABCD)
Ta có :
đồng phẳng.
3. Điều kiện để ba vecto đồng phẳng.
- Định lí 1.
Trong không gian cho hai vecto không cùng phương và vecto . Khi đó, ba vecto đồng phẳng khi và chỉ khi có cặp số m; n sao cho . Ngoài ra, cặp số m; n là suy nhất.
- Định lí 2.
Trong không gian cho ba vecto không đồng phẳng . Khi đó, với mọi vecto ta đều tìm được một bộ ba số m, n, p sao cho . Ngoài ra, bộ ba số m; n; p là duy nhất.
Ví dụ 3. Cho hình lăng trụ ABC.A’B’C’ gọi M là trung điểm của BB’ . Đặt . Phân tích vecto theo .
Lời giải:
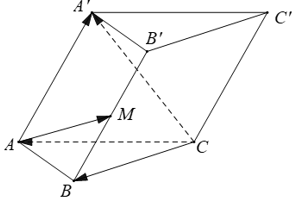
Áp dụng quy tắc 3 điểm và quy tắc hiệu hai vecto ta có :
(vì M là trung điểm của BB’) .