Tailieumoi.vn xin giới thiệu Bài tập Toán 11 Chương 5 Bài 3: Đạo hàm của hàm số lượng giác. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 5 Bài 3: Đạo hàm của hàm số lượng giác. Mời các bạn đón xem:
Bài tập Toán 11 Chương 5 Bài 3: Đạo hàm của các hàm số lượng giác
A. Bài tập Đạo hàm của hàm số lượng giác.
I. Bài tập trắc nghiệm
Bài 1: Hàm số y = (1 + sinx)(1 + cosx) có đạo hàm là:
A. y' = cosx - sinx + 1.
B. y' = cosx + sinx + cos2x.
C. y' = cosx - sinx + cos2x.
D. y' = cosx + sinx + 1.
Chọn đáp án C
Bài 2: Cho hàm số y = f(x) = sin + cos. Giá trị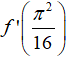 
bằng:
Chọn đáp án A
Bài 3: Cho hàm số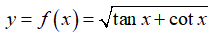 
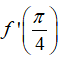
. Giá trị 
bằng:
Chọn đáp án C
Bài 4: Cho hàm số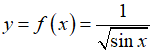 
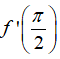
. Giá trị 
bằng:
A.1
B. .
C. 0
D. Không tồn tại.
Chọn đáp án C
Bài 5: Cho hàm số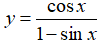 
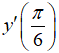
. Tính 
bằng:
Chọn đáp án C
Bài 6: Cho hàm số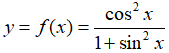 
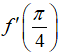
. Biểu thức 
bằng
Chọn đáp án C
Bài 7: Hàm số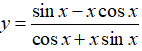 
có đạo hàm bằng
Chọn đáp án D
Bài 8: Cho hàm số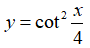 
. Khi đó nghiệm của phương trình là:
A. π + k2π.
B. 2π + k4π.
C. 2π + kπ.
D. π + kπ.
Chọn đáp án B
Bài 9: Hàm số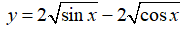 
có đạo hàm là:
Chọn đáp án C
Bài 10: Tính đạo hàm của hàm số sau: y = 2sin24x - 3cos35x.
Chọn đáp án D
II. Bài tập tự luận có lời giải
Bài 1: Tính đạo hàm của hàm số sau: y = (2 + sin22x)3.
Lời giải:
Bài 2: Đạo hàm của hàm số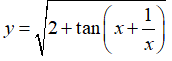 
là
Lời giải:n
Bài 3: Đạo hàm của hàm số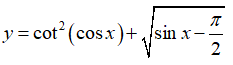 
là
Lời giải:
Bài 4: Hàm số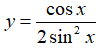 
có đạo hàm bằng:
Lời giải:
Bài 5: Tính đạo hàm của hàm số sau: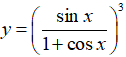 
.
Lời giải:
Bài 6: Tính đạo hàm của hàm số sau: y = sin(cos2x.tan2x).
Lời giải:
Bài 7: Tính đạo hàm của hàm số sau: 
Lời giải:
Bài 8: Tính đạo hàm của hàm số sau: y = sin2(cos(tan43x))
Lời giải:
Bài 10:
Lời giải:
Bài 10: Đạo hàm của hàm số
bằng biểu thức nào?
Lời giải:
Bài 11: Tính đạo hàm của hàm số y= sin (2x+ 8)?
A. 2 cos(2x+ 8) B. cos( 2x+ 8) C. –cos( 2x+ 8) D. -2cos( 2x+ 8)
Lời giải:
+ áp dụng công thức đạo hàm của hàm hợp ta có;
y'=cos( 2x+8).( 2x+8)' = 2cos( 2x+ 8)
Chọn A.
Bài 12: Tính đạo hàm của hàm số: y= cos( x2+ 7x- 9)?
A.- sin( x2 + 7x- 9) B.- sin ( x2+ 7x – 9)( x2+ 7x- 9)
C. – (2x+7). sin(x2 + 7x- 9) D. sin(x2+ 7x- 9)( 2x+7)
Lời giải:
Áp dụng công thức đạo hàm của hàm hợp ta có:
y'= -sin(x2+7x-9).(x2+7x-9)' = - sin(x2+ 7x- 9).( 2x+ 7).
Chọn C.
Bài 13: Tính đạo hàm của hàm số: y= sin 8x+ cos 2x
A. cos8x – sin2x B. 8 cos8x – 2sin 2x
C. 8.cos8x + 2sin2x D. – cos8x + sin 2x
Lời giải:
Ta có: y'=( sin8x)'+(cos2x)'=8 cos8x-2 sin2x
Chọn B.
III. Bài tập vận dụng
Bài 1 Đạo hàm của hàm số
bằng biểu thức nào sau đây?
Bài 2 Tính đạo hàm của hàm số y = x.cosx.
Bài 3 Tính đạo hàm của hàm số sau: y = sin3(2x + 1) .
Bài 4 Tính đạo hàm của hàm số sau: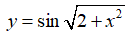 
.
Bài 5 Tính đạo hàm của hàm số sau: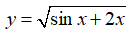 
.
Bài 6 Hàm số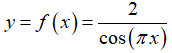 
có f'(3) bằng?
Bài 7 Cho hàm số y = cos3x.sin2x. Tính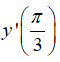 
Bài 8 Cho hàm số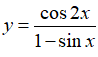 
. Tính 
Bài 9 Cho hàm số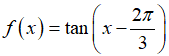 
. Giá trị bằng?
Bài 10 Cho hàm số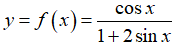 
. Tính f'(x)
B. Lý thuyết Đạo hàm của hàm số lượng giác
1. Giới hạn
Định lý 1.
Ví dụ 1. Tính
Lời giải
Đặt x – 1 = t.
Khi x tiến đến 1 thì t tiến đến 0.
2. Đạo hàm của hàm số y = sinx
Định lý 2.
Hàm số y = sinx có đạo hàm tại mọi và (sinx)’ = cosx.
QUẢNG CÁO
Chú ý:
Nếu y = sinu và u = u(x) thì: (sinu)’ = u’.cosu
Ví dụ 2. Tính đạo hàm của hàm số
Lời giải
3. Đạo hàm của hàm số y = cosx
Định lý 3.
Hàm số y = cosx có đạo hàm tại mọi và (cosx)’ = - sinx.
Chú ý:
Nếu y = cosu và u = u(x) thì: (cosu)’ = - u’.sinu
Ví dụ 3. Tính đạo hàm của hàm số tại .
Lời giải
Đặt
Thay vào y’ ta được:
Vậy giá trị của đạo hàm của hàm số tại là
4. Đạo hàm của hàm số y = tanx
Định lý 4.
Hàm số y = tanx có đạo hàm tại mọi và (tanx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (tanu)’ =
Ví dụ 4. Tính đạo hàm
Lời giải
Đặt u = 2 + tanx
5. Đạo hàm của hàm số y = cotx
Định lý 5.
Hàm số y = cotx có đạo hàm tại mọi và (cotx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (cotu)’ =
Ví dụ 5. Tính đạo hàm của hàm y = cot x2.
Lời giải
y’ = (cot x2)’ = (x2)’.=.
6. Bảng quy tắc tính đạo hàm tổng hợp:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
