Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 10 sách Chân trời sáng tạo năm 2024 – 2025. Tài liệu gồm 2 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 1 Toán 10. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 10 Chân trời sáng tạo bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây
Xem thử tài liệu tại đây: Link tài liệu
Đề thi Học kì 1 Toán lớp 10 Chân trời sáng tạo có đáp án năm 2024 - 2025 - Đề 1
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 1)
Phần I: Trắc nghiệm (6 điểm – 30 câu).
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi!
b) Số 15 là số nguyên tố.
c) Tổng các góc của một tam giác là
d) là số nguyên dương.
A. 3 B. 2
C. 4 D. 1
Câu 2: Trong các mệnh đề dưới đây mệnh đề nào đúng?
A.
B.
C.
D. chia hết cho 4.
Câu 3: Cho và . Hãy chọn khẳng định đúng.
A.
B.
C.
D.
Câu 4: Cho , là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?
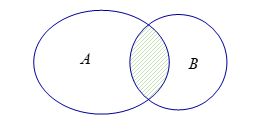
A. B.
C. D.
Câu 5: Trong số học sinh của lớp 10A có bạn được xếp loại học lực giỏi, bạn được xếp loại hạnh kiểm tốt, trong đó có bạn vừa được xếp loại học lực giỏi vừa được xếp loại hạnh kiểm tốt. Khi đó, lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hoặc hạnh kiểm tốt.
A. 20 B. 30
C. 35 D. 25
Câu 6: Cho ; . Điều kiện để là
A. B.
C. D.
Câu 7: Trong các cặp số sau đây, cặp nào là nghiệm của bất phương trình
A.
B.
C.
D.
Câu 7: Hình dưới đây là hình biểu diễn của bất phương trình nào (miền nghiệm là miền màu xanh)?
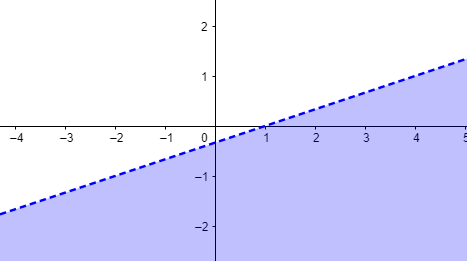
A. B.
C. D.
Câu 8: Miền nghiệm của bất phương trình: là mặt phẳng chứa điểm.
A. (3,0) B. (3,1)
C. (2,1) D. (0,0)
Câu 9: Công việc nào sau đây không phụ thuộc vào các công việc của môn thống kê ?
A. Thu thập số liệu.
B. Trình bày số liệu.
C. Phân tích và xử lý số liệu.
D. Ra quyết định dựa trên số liệu
Câu 10: Cho mẫu số liệu thống kê .Mốt của mẫu số liệu trên bằng bao nhiêu?
A. 5 B. 10
C. 2 D. 6
Câu 11: Cho dãy số liệu thống kê: 48,36,33,38,32,48,42,33,39. Khi đó số trung vị là
A. 32 B. 36
C. 38 D. 40
Câu 12: Cho dãy số liệu thống kê: .Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 12 B. 14
C. 13 D. 12.5
Câu 13: Điều tra về số học sinh của 1 trường THPT có 1120 học sinh khối 10, 1075 học sinh khối 11 và 900 học sinh khối 12. Hỏi kích thước mấu là bao nhiêu?
A. 1220 B. 1075
C. 900 D. 3095
Câu 14: Chọn câu đúng trong bốn phương án trả lời đúng sau đây: độ lệch chuẩn là:
A. Bình phương của phương sai.
B. Một nửa của phương sai.
C. Căn bậc hai phương sai.
D. Không phải các công thức trên.
Câu 15: Tìm tập xác định của hàm số
A. B.
C. D.
Câu 16: Điểm nào sau đây không thuộc đồ thị hàm số
A.
B.
C.
D.
Câu 17: Cho hàm số Tính
A. B.
C. D.
Câu 18: Xét tính đồng biến, nghịch biến của hàm số trên khoảng và trên khoảng . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên , đồng biến trên .
B. Hàm số đồng biến trên , nghịch biến trên .
C. Hàm số nghịch biến trên các khoảng và .
D. Hàm số đồng biến trên các khoảng và .
Câu 19: Cho hàm số bậc hai . Trục đối xứng của đồ thị hàm số là:
A. B.
C. D.
Câu 20: Tìm tất cả các giá trị thực của tham số để hàm số xác định trên
A. B.
C. D.
Câu 21: Tam giác có . Số đo góc bằng:
A. B.
C. D.
Câu 22: Tam giác có và . Tính độ dài cạnh .
A.
B.
C.
D.
Câu 23: Tam giác có . Tính bán kính của đường tròn ngoại tiếp tam giác .
A.
B.
C.
D.
Câu 24: Tam giác vuông tại có cm, cm. Tính bán kính của đường tròn nội tiếp tam giác đã cho.
A. cm. B. cm
C. cm. D. cm.
Câu 25: Cho hai điểm và phân biệt. Điều kiện để là trung điểm là:
A.
B.
C.
D.
Câu 26: Cho . Khẳng định nào sau đây đúng?
A. và cùng hướng.
B. và cùng độ dài.
C. là hình bình hành.
D.
Câu 27: Cho hình bình hành có là giao điểm của hai đường chéo. Hỏi vectơ bằng vectơ nào trong các vectơ sau?
A.
B.
C.
D.
Câu 28: Cho hình vuông cạnh Tính
A.
B.
C.
D.
Câu 29: Cho hình thoi có và Tính
A.
B.
C.
D.
Câu 30: Cho hình bình hành có , góc nhọn và diện tích bằng Tính
A.
B.
C.
D.
Phần II. Tự luận (4 điểm):
Câu 1:
a. Cho hai tập hợp và . Tìm .
b. Cho là một tham số thực và hai tập hợp , . Tìm các giá trị để .
Câu 2: Cho hàm số có đồ thị (P). Biết hàm số đi qua M (3, 0)
a. Xác định hàm số
b. Vẽ bảng biến thiên, vẽ đồ thị (P).
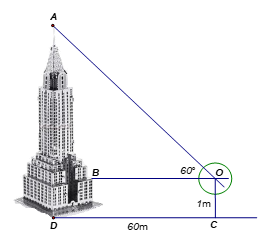
Câu 3: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng , giả sử chiều cao của giác kế là . Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh của tháp. Đọc trên giác kế số đo của góc . Tính chiều cao của tháp, làm tròn kết quả đến hàng phần trăm.
Câu 4: Tìm tập các hợp điểm thỏa mãn với là ba đỉnh của tam giác.
Hướng dẫn giải:
Phần I: Trắc nghiệm (6 điểm)
|
1.B |
2.A |
3.A |
4.D |
5.B |
6.C |
7.A |
8.C |
9.D |
10.A |
|
11.C |
12.A |
13.D |
14.C |
15.C |
16.C |
17.C |
18.B |
19.A |
20.D |
|
21.C |
22.B |
23.C |
24.C |
25.C |
26.B |
27.B |
28.A |
29.D |
30.D |
Câu 1 (NB):
Phương pháp:
Mệnh đề có tính đúng hoặc sai.
Cách giải:
b, c là mệnh đề
Chọn B.
Câu 2 (NB):
Phương pháp:
Tìm giá trị để mệnh đề đúng hoặc sai để khẳng định.
Cách giải:
A: Đúng vì nên .
Chọn A.
Câu 3 (TH):
Phương pháp:
Dùng định nghĩa các phép toán trên tập hợp.
Cách giải:
A. Đúng vì vừa thuộc tập A, vừa thuộc tập B.
B. HS nhầm là vừa thuộc A hoặc B.
C. HS nhầm là thuộc A và không thuộc B.
D. HS nhầm là thuộc B và không thuộc A.
Chọn A.
Câu 4 (NB):
Phương pháp:
Cách giải:
Theo biểu đồ Ven thì phần gạch sọc trong hình vẽ là tập hợp .
Chọn D.
Câu 5 (TH):
Phương pháp:
Tính số học sinh chỉ xếp loại giỏi, chỉ xếp hạnh kiểm tốt. Từ đó tính số học sinh có học lực giỏi hoặc hạnh kiểm tốt.
Cách giải:
Từ giả thiết bài toán, ta có:
Số các học sinh chỉ có học lực giỏi là: .
Số các học sinh chỉ được xếp loại hạnh kiểm tốt là: .
Tổng số học sinh có học lực giỏi hoặc hạnh kiểm tốt là .
Vậy có học sinh được khen thưởng.
Chọn B.
Câu 6 (VD):
Phương pháp:
Dùng định nghĩa phép toán trên tập hợp hoặc vẽ tia số.
Cách giải:
Ta có: .
Chọn C.
Câu 7 (NB):
Phương pháp:
Thay tọa độ x, y vào bât phương trình và kiểm tra tính đúng sai
Cách giải:
Vì 2.0+3.0 = 0 <1 nên (0,0) thuộc miền nghiệm của bất phương trình
Chọn D.
Câu 7 (TH):
Phương pháp:
Lấy điểm bất kì thuộc hoặc không thuộc miền nghiệm để kiểm tra bất phương trình trong đáp án
Cách giải:
Ta thấy O(0,0) không thuộc miền nghiệm nên loại B,C
Đường thẳng qua (1,0) nên đáp án A đúng
Chọn A.
Câu 8 (TH):
Phương pháp:
Rút gọn bất phương trình và thay tọa độ các điểm vào bất phương trình để kiểm tra tính đúng sai.
Cách giải:
Vì thay x = 2, y = 1 vào bất phương trình ta thấy – 2 + 3.1 =1 nên (2,1) thuộc miền nghiệm
Chọn C.
Câu 9 (NB):
Phương pháp:
Cách giải:
Ra quyết định dựa trên số liệu không phụ thuộc vào công việc của môn Thống kê.
Chọn D.
Câu 10 (NB):
Phương pháp:
Mốt của dấu hiệu là giá trị có tần số lớn nhất.
Cách giải:
Vì 5 có tần suất là 2, còn 6,2,9,10,8 đều có tần suất là 1 nên mốt của dấu hiệu là 5.
Chọn A.
Câu 11 (TH):
Phương pháp:
Lập bảng tần số, sắp xếp các giá trị thống kê theo thứ tự không giảm.
Nếu có n (n lẻ) n = 2k+1 giá trị thì số trung vị bằng giá trị thứ k
Nếu có n (chẵn) n= 2k giá trị thì số trung vị bằng trung bình cộng 2 giá trị k-1 và k+1.
Cách giải:
|
32 |
33 |
36 |
38 |
39 |
42 |
48 |
|
1 |
2 |
1 |
1 |
1 |
1 |
2 |
Vì có 7 giá trị nên trung vị bằng số liệu thứ 4 là 38
Chọn C.
Câu 12 (TH):
Phương pháp:
Số trung bình là
Cách giải:
Chọn A.
Câu 13 (TH):
Phương pháp:
Kích thước mẫu là số các số liệu thống kê.
Cách giải:
Kích thước mẫu bằng 1120+1075+900 = 3095
Chọn D.
Câu 14 (NB):
Phương pháp:
Độ lệch chuẩn là căn bậc hai của phương sai.
Cách giải:
Độ lệch chuẩn là căn bậc hai của phương sai.
Chọn C.
Câu 15 (TH):
Phương pháp:
Chú ý không rút gọn biểu thức trước khi tìm tập xác định.
Cách giải:
Hàm số xác định khi
Vậy tập xác định của hàm số là
Chọn C.
Câu 16 (TH):
Phương pháp:
Thay tọa độ từng điểm và kiểm tra.
Cách giải:
Xét đáp án A, thay và vào hàm số ta được: thỏa mãn.
Xét đáp án B, thay và vào hàm số ta được : thỏa mãn.
Xét đáp án C, thay và vào hàm số ta được không thỏa mãn.
Chọn C.
Câu 17 (TH):
Phương pháp:
Kiểm tra các giá trị cần tính thuộc điều kiện nào của hàm số trước khi tính.
Cách giải:
Khi thì
Khi thì .. Vậy
Chọn C.
Câu 18 (TH):
Phương pháp:
Tìm đỉnh dồ thị hàm số và vẽ bảng biến thiên.
Cách giải:
Đỉnh S (2, 1), bề lõm quay lên nên hàm số đồng biến trên và nghịch biến trên .
Chọn B.
Câu 19 (TH):
Phương pháp:
Trục đối xứng của hàm số bậc hai là
Cách giải:
Trục đối xứng của hàm số bậc hai là
Chọn A.
Câu 20 (VDC):
Phương pháp:
Tìm tập xác định của hàm số theo m
Cho tập hợp tìm được là tập con của
Cách giải:
Hàm số xác định khi .
TH1: Nếu thì . Suy ra tập xác định của hàm số là
Khi đó, hàm số xác định trên khi và chỉ khi .Không thỏa mãn điều kiện .
TH2: Nếu thì . Suy ra tập xác định của hàm số là .
Khi đó, hàm số xác định trên khi và chỉ khi (Thỏa mãn điều kiện ). Vậy thỏa yêu cầu bài toán.
Chọn D.
Câu 21 (NB):
Phương pháp:
Áp dụng định lý cosin
Cách giải:
Chọn C.
Câu 22 (TH):
Phương pháp:
Áp dụng định lý cosin
Cách giải:
Theo định lí hàm cosin, ta có
Chọn B.
Câu 23 (TH):
Phương pháp
Áp dụng công thức Herong.
Cách giải:
Đặt Áp dụng công thức Hê – rông, ta có
Vậy bán kính cần tìm là
Chọn C.
Câu 24 (TH):
Phương pháp:
Dùng công thức
Cách giải:
Dùng Pitago tính được , suy ra .
Diện tích tam giác vuông .Lại có
Chọn C.
Câu 25 (NB):
Phương pháp:
I là trung điểm của AB thì IA = IB và , ngược hướng
Cách giải:
IA = IB và , ngược hướng nên
Chọn C.
Câu 26 (TH):
Phương pháp:
Dùng định nghĩa hai vecto bằng nhau.
Cách giải:
Ta có . Do đó:
và ngược hướng.
và cùng độ dài.
là hình bình hành nếu và không cùng giá.
Chọn B.
Câu 27 (NB):
Phương pháp:
Dùng quy tắc cộng hai veto và hai vecto bằng nhau.
Cách giải:
Chọn B.
Câu 28 (NB):
Phương pháp:
Tích vô hướng
Cách giải:
Ta có nên .
Chọn A.
Câu 29 (TH):
Phương pháp:
Tích vô hướng
Cách giải:
Gọi giao điểm của AC và BD là O, giả thiết không cho góc, ta phân tích các vectơ theo các vectơ có giá vuông góc với nhau.
Ta có .
Chọn D.
Câu 30 (VD):
Phương pháp:
Tích vô hướng
Cách giải:
Ta có . Diện tích tam giác ABC là:
Mặt khác góc giữa hai vecto là góc ngoài góc .
Suy ra .
Chọn D.
Phần II: Tự luận (4 điểm)
Câu 1 (TH):
Phương pháp:
Dùng định nghĩa hoặc biểu diễn trên tia số.
Cách giải:
a. Biểu diễn trên trục số ta được:
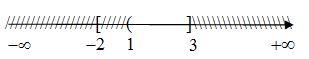
b. Ta có , .
.
Câu 2 (TH):
Phương pháp:
Xác định đỉnh, trục đối xứng, các điểm mà đồ thị đi qua
Cách giải:
a. Vì đi qua M (3, 0) nên thay x = 3, y = 0 ta có
0 = 9 – 2(m + 1).3 + 3m - 3. Suy ra 9 – 6m – 6 + 3m – 3 = 0. Suy ra m = 0.
Vậy hàm số là
b. Đỉnh S của (P) có hoành độ . Suy ra tung độ đỉnh S là y = 1 – 2 - 3 = - 4.
Vậy S (1, - 4), trục đối xứng x = 1
Bảng biến thiên:
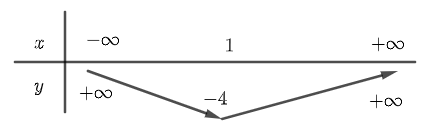
Đồ thị:
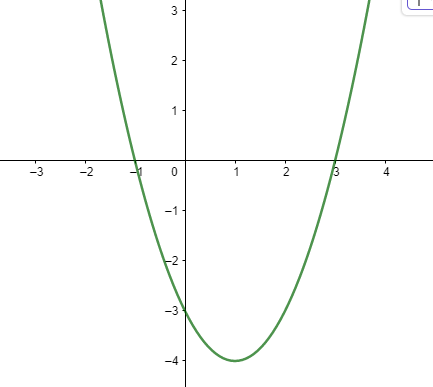
Đồ thị hàm số là 1 parabol có bề lõm quay lên, có đỉnh S (1,-4), trục đối xứng x = 1, cắt trục tung tại (0, -3), có giá trị nhỏ nhất bằng 0
Câu 3 (TH):
Phương pháp:
Dùng giá trị lượng giác trong tam giác vuông.
Cách giải:
Xét tam giác ABO vuông tại B. Khi đó m
Ta có BD = OC =1 m.
Vậy chiều cao của tháp là AB + BD = m
Câu 4 (TH):
Phương pháp:
Tính chất trọng tâm tam giác, chứng minh .
Cách giải:
Gọi G là trọng tâm tam giác ABC. Suy ra
Ta có
Chứng tỏ hay M nhìn đoạn BG dưới một góc vuông nên tập hợp các điểm M là đường tròn đường kính BG.
Đề thi Học kì 1 Toán lớp 10 Chân trời sáng tạo có đáp án năm 2024 - 2025 - Đề 2
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 2)
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
|
TT |
Nội dung kiến |
Đơn vị kiến thức |
Mức độ nhận thức |
Tổng |
% |
|||||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
Số CH |
Thời |
|||||||||
|
Số |
Thời |
Số |
Thời |
Số |
Thời gian (phút) |
Số |
Thời |
TN |
TL |
|||||
|
1 |
1. Mệnh đề. Tập hợp |
1.1. Mệnh đề |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
3 |
4 |
|
1.2. Tập hợp. Các phép toán trên tập hợp |
|
|
1 |
2 |
|
|
|
|
1 |
0 |
||||
|
2 |
2. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
Bất phương trình, hệ bất phương trình bậc nhất hai ẩn và ứng dụng |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
1 |
2 |
|
3 |
3. Hàm số bậc |
3.1. Hàm số và đồ thị |
1 |
1 |
2 |
4 |
|
|
|
|
3 |
0 |
24 |
22 |
|
3.2. Hàm số bậc hai |
1 |
1 |
2 |
4 |
1 |
6 |
1 |
8 |
3 |
2 |
||||
|
4 |
4. Hệ thức lượng trong tam giác |
4.1. Giá trị lượng giác của một góc từ 0° đến 180° |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
12 |
10 |
|
4.1. Định lí côsin và định lí sin |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
||||
|
4.2. Giải tam giác và ứng dụng thực tế |
|
|
|
|
1 |
6 |
|
|
1 |
0 |
||||
|
5 |
5. Vectơ |
5.1. Khái niệm vectơ |
2 |
2 |
1 |
2 |
|
|
|
|
3 |
0 |
31 |
34 |
|
5.2. Tổng và hiệu của hai vectơ |
1 |
1 |
3 |
6 |
|
|
|
|
4 |
0 |
||||
|
5.3. Tích của vectơ với một số |
1 |
1 |
1 |
2 |
1 |
6 |
1 |
7 |
3 |
1 |
||||
|
5.4. Tích vô hướng của 2 vectơ |
|
|
2 |
4 |
|
|
|
|
2 |
0 |
||||
|
6 |
6. Số đúng và số gần đúng |
6.1. Số gần đúng |
2 |
2 |
2 |
4 |
|
|
|
|
4 |
0 |
19 |
28 |
|
6.2. Mô tả bằng bảng dữ liệu |
2 |
2 |
|
|
|
|
|
|
2 |
0 |
||||
|
6.3. Các số đặc trưng đo xu thế trung tâm |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
||||
|
|
|
6.4. Các số đặc trưng đo độ phân tán |
|
|
1 |
2 |
1 |
6 |
|
|
1 |
1 |
||
|
Tổng |
|
15 |
15 |
18 |
36 |
4 |
24 |
2 |
15 |
35 |
4 |
90 |
|
|
|
Tỉ lệ (%) |
|
|
|
|
|
70 |
30 |
|
100 |
|||||
|
Tỉ lệ chung (%) |
|
|
|
|
|
|
100 |
|||||||
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút
|
TT |
Nội dung |
Đơn vị |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ nhận thức |
|||
|
Nhận |
Thông |
Vận |
Vận dụng |
||||
|
1 |
1. Mệnh |
1.1. Mệnh đề |
Nhận biết: – Nhận biết được thế nào là mệnh đề toán học, tính đúng/sai của các mệnh đề toán học trong trường hợp đơn giản. |
1 |
|
|
|
|
1.2. Tập hợp. Các phép toán trên tập hợp |
Thông hiểu – Thực hiện được phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù của một tập con) và biết dùng biểu đồ Ven để biểu diễn chúng trong những trường hợp cụ thể. |
|
1 |
|
|
||
|
2 |
2. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
Bất phương trình, hệ bất phương trình bậc nhất hai ẩn và ứng dụng |
Nhận biết: – Nhận biết được bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
1 |
|
|
|
|
3 |
3. Hàm số bậc hai và đồ thị |
3.1. Hàm số và đồ thị |
Nhận biết: – Nhận biết được những mô hình thực tế (dạng bảng, biểu đồ, công thức) dẫn đến khái niệm hàm số. Thông hiểu: – Mô tả được các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá trị, hàm số đồng biến, hàm số nghịch biến, đồ thị của hàm số. – Mô tả được các đặc trưng hình học của đồ thị hàm số đồng biến, hàm số nghịch biến. |
1 |
2 |
|
|
|
3.2. Hàm số bậc hai |
Nhận biết: – Nhận biết được các tính chất cơ bản của Parabol như đỉnh, trục đối xứng. Thông hiểu: – Tính được bảng giá trị của hàm số bậc hai. – Vẽ được Parabol (parabol) là đồ thị hàm số bậc hai. – Nhận biết và giải thích được các tính chất của hàm số bậc hai thông qua đồ thị. Vận dụng: – Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn. (ví dụ: xác định độ cao của cầu, cổng có hình dạng Parabol, ...). Vận dụng cao: - Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết các bài toán chứa tham số. |
1 |
2 |
1 |
1 |
||
|
4 |
4. Hệ thức lượng trong tam giác |
4.1. Giá trị lượng giác của một góc từ 0° đến 180° |
Nhận biết: – Nhận biết được giá trị lượng giác của một góc từ 0° đến 180°. – Nhận biết được hệ thức liên hệ giữa giá trị lượng giác của các góc phụ nhau, bù nhau. Thông hiểu: – Tính được giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng máy tính cầm tay. |
1 |
1 |
|
|
|
4.2. Định lí côsin và định lí sin |
Thông hiểu: – Tính được giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng máy tính cầm tay. – Giải thích được các hệ thức lượng cơ bản trong tam giác: định lí côsin, định lí sin, công thức tính diện tích tam giác. |
1 |
1 |
|
|
||
|
4.3. Giải tam giác và ứng dụng thực tế |
Vận dụng: – Mô tả được cách giải tam giác và vận dụng được vào việc giải một số bài toán có nội dung thực tiễn (ví dụ: xác định khoảng cách giữa hai địa điểm khi gặp vật cản, xác định chiều cao của vật khi không thể đo trực tiếp,...). |
|
|
1 |
|
||
|
5 |
5. Vectơ |
5.1. Khái niệm vectơ |
Nhận biết: – Nhận biết được khái niệm vectơ, vectơ bằng nhau, vectơ-không. Thông hiểu: – Mô tả được một số đại lượng trong thực tiễn bằng vectơ. – Thực hiện được các phép toán trên vectơ (tổng và hiệu hai vectơ, tích của một số với vectơ, tích vô hướng của hai vectơ) và mô tả được những tính chất hình học (ba điểm thẳng hàng, trung điểm của đoạn thẳng, trọng tâm của tam giác,...) bằng vectơ. Vận dụng: – Sử dụng được vectơ và các phép toán trên vectơ để giải thích một số hiện tượng có liên quan đến Vật lí và Hoá học (ví dụ: những vấn đề liên quan đến lực, đến chuyển động,...). – Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán liên quan đến thực tiễn (ví dụ: xác định lực tác dụng lên vật,...) Vận dụng cao: - Tìm tập hợp các điểm thỏa mãn một đẳng thức vectơ. |
2 |
1 |
|
|
|
5.2. Tổng và hiệu của hai vectơ |
1 |
3 |
|
|
|||
|
5.3. Tích của vectơ với một số |
1 |
1 |
1 |
1 |
|||
|
5.4. Tích vô hướng của 2 vectơ |
|
2 |
|
|
|||
|
6 |
6. Số đúng và số gần đúng |
6.1. Số gần đúng |
Nhận biết: - Nhận biết được khái niệm số đúng, số gần đúng, độ chính xác. - Biết được cách biểu diễn số liệu bằng bảng hoặc biểu đồ. Thông hiểu: - Biết cách tính các số đo xu thế trung tâm, các số đặc trưng cho độ phân tán của mẫu số liệu. - Biết được ý nghĩa của các số đo xu thế trung tâm, các số đặc trưng đo độ phân tán được sử dụng. |
2 |
2 |
|
|
|
6.2. Mô tả bằng bảng dữ liệu |
2 |
|
|
|
|||
|
6.3. Các số đặc trưng đo xu thế trung tâm |
1 |
1 |
|
|
|||
|
6.4. Các số đặc trưng đo độ phân tán |
|
1 |
1 |
|
|||
|
Tổng |
|
15 |
18 |
4 |
2 |
||
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. Câu nào sau đây không là mệnh đề?
A. Bạn học giỏi quá!;
B. Tam giác đều là tam giác có ba cạnh bằng nhau;
C. 3 < 1;
D. 4 – 5 = 1.
Câu 2. Tập xác định D của hàm số là
A. D = [– 2; 2] \ {0};
B. D = [– 2; 2];
C. D = (– 2; 2);
D. D = ℝ.
Câu 3. Cho A = (– 1; 5] và B = (2; 7). Tập hợp A ∩ B bằng:
A. (2; 5];
B. [2; 5];
C. (2; 5);
D. [2; 5).
Câu 4. Cho tập hợp , . Tất cả giá trị của m để là
A. m ≤ 2;
B. m ≥ – 1;
C. m > 2;
D. m > – 2.
Câu 5. Miền nghiệm của hệ bất phương trình là
A. Miền tam giác;
B. Một nửa mặt phẳng;
C. Miền ngũ giác;
D. Miền tứ giác.
Câu 6. Giá trị cos113° + cos45° + cos67° bằng
A. ;
B. 1;
C. ;
D. 0.
Câu 7. Cho tam giác ABC có AC = 2, BC = 5 và . Số đo của góc A là:
A. 50°35’;
B. 51°34’;
C. 77°25’;
D. 7°6’.
Câu 8. Trong tam giác ABC, khẳng định nào sau đây đúng?
Câu 9. Cho hai vectơ và thỏa mãn và . Góc giữa hai vectơ và bằng
A. 30°;
B. 90° ;
C. 60° ;
D. 45°.
Câu 10. Cho hình vuông ABCD tâm O cạnh a. Tính ta được :
Câu 11. Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
A. 12,096;
B. 12,09638;
C. 12,0964;
D. 12,10.
Câu 12. Cho hình vuông ABCD. Vectơ bằng vectơ nào sau đây?
Câu 13. Cho hình thang ABCD . Mệnh đề nào dưới đây đúng?
A. Hai vectơ cùng phương;
B. Hai vectơ cùng hướng;
C. Hai vectơ cùng phương;
D. Hai vectơ ngược hướng.
Câu 14. Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
A. y = – 2x2 + 4x + 1;
B. y = 2x2 + 4x + 3;
C. y = 2x2 – 2x + 1;
D. y = x2 – x + 5.
Câu 15. Cho hình bình hành ABCD . Đẳng thức vectơ nào sau đây đúng:
Câu 16. Cho tam giác ABC vuông tại A, , M là trung điểm của BC và có . Tính cạnh AB, AC:
A. AB = a, AC = ;
B. AB = , AC = ;
C. AB = a, AC = a;
D. AB = , AC = a.
Câu 17. Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
A. 1,24;
B. 1,2;
C. 1,236;
D. 1.
Câu 18. Hàm số nào dưới đây là hàm nghịch biến với mọi x ∈ ℝ?
A. y = 2x + 1;
B. y = – |x|;
C. y = x2 + 2x;
D. y = x – 1.
Câu 19. Cho các hàm số: f(x) = , g(x) = và h(x) = x2 – x. Trong các hàm số đã cho, số hàm chẵn là:
A. 0;
B. 1;
C. 2;
D. 3.
Câu 20. Cho hàm số y = (m – 2021)x + m – 2. Điều kiện để hàm số đồng biến trên ℝ là
A. m < 2021;
B. m > 2021;
C. 2 < m < 2021;
D. m ≥ 2021.
Câu 21. Cho bảng biến thiên sau:
Đồ thị hàm số bậc hai tương ứng với bảng biến thiên trên là :
A. y = x2 + 2x – 1;
B. y = x2 – 2x + 2;
C. y = 2x2 – 4x + 4;
D. y = – 3x2 + 6x – 1.
Câu 22. Cho hình chữ nhật ABCD tâm O. Gọi E, F lần lượt là trung điểm của OA và CD. Biết . Tính giá trị biểu thức a + b:
A. ;
B. ;
C. ;
D. 1.
Câu 23. Giá trị ngoại lệ trong mẫu là
A. giá trị ở chính giữa trong dãy không giảm của mẫu số liệu;
B. giá trị xuất hiện nhiều nhất trong các giá trị của mẫu số liệu;
C. giá trị quá nhỏ hay quá lớn với đa số các giá trị của mẫu số liệu;
D. giá trị trung bình cộng của các giá trị của mẫu số liệu.
Câu 24. Số liệu xuất hiện nhiều nhất trong mẫu số liệu được gọi là:
A. Số trung bình cộng;
B. Trung vị;
C. Tứ phân vị;
D. Mốt.
Câu 25. Hàm số bậc hai có bảng biến thiên như hình vẽ có tọa độ điểm đỉnh là
A. I(– 3; 3);
B. I(0; – 3);
C. I(– 3; 0);
D. I(0; 0).
Câu 26. Cho điểm I là trung điểm của đoạn thẳng AB. Hỏi đẳng thức nào sau đây đúng?
Câu 27. Tìm m để hàm số y = (2m – 3)x + m + 1 đồng biến trên .
Câu 28. Cho hình thoi ABCD có cạnh bằng a và . Độ dài bằng
Câu 29. Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?
Câu 30. Cho hàm số y = f(x) có bảng biến thiên như sau. Hàm số đã cho đồng biến trên khoảng:
Câu 31. Chu vi của hình chữ nhật có chiều rộng là x = 3,456 ± 0,01 và chiều dài là y = 12,732 ± 0,015 và ước lượng sai số tuyệt đối mắc phải là
A. C = 32,376 ± 0,025; ∆C ≤ 0,05;
B. C = 32,376 ± 0,05; ∆C ≤ 0,025;
C. C = 32,376 ± 0,5; ∆C ≤ 0,5;
D. C = 32,376 ± 0,05; ∆C ≤ 0,05.
Câu 32. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng ở vị trí C. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 25° và 42°. Biết khoảng cách giữa hai vị trí A và B là 80 m. Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
A. 116 m;
B. 78 m;
C. 104 m;
D. 86 m.
Câu 33. Kết quả điều tra số con của 30 hộ gia đình thuộc một thôn được ghi lại trong bảng sau:
Số trung vị của dãy số liệu trên là
A. 3;
B. 2,5;
C. 2;
D. 4.
Câu 34. Biểu đồ dưới đây thể hiện diện tích lúa cả năm của hai tỉnh An Giang và Kiên Giang từ năm 2010 đến năm 2019 (đơn vị: nghìn hecta):
Trong khoảng từ năm 2010 đến 2013 năm mà diện tích lúa tỉnh Kiên Giang gần gấp 1,2 lần diện tích lúa của tỉnh An Giang nhất là
A. 2010;
B. 2011;
C. 2012;
D. 2013.
Câu 35. Cho tam giác ABC có các góc . Tỉ số bằng
II. PHẦN TỰ LUẬN (3 điểm)
Bài 1 (1,0 điểm). Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải bán với giá bao nhiêu sau khi giảm giá để lợi nhuận thu được là cao nhất.
Bài 2 (1,0 điểm). Cho tam giác ABC có G là trọng tâm. Gọi D và E lần lượt là các điểm thỏa mãn đẳng thức .
a) Phân tích vectơ theo hai vectơ và .
b) Tìm x để ba điểm D, G, E thẳng hàng. Với giá trị tìm được của x, hãy tính tỉ số .
Bài 3 (1,0 điểm). Người ta tiến hành phỏng vấn một số người về chất lượng của một sản phẩm mới, người điều tra yêu cầu cho điểm sản phẩm (thang điểm 100) kết quả như sau:
|
80 |
65 |
51 |
58 |
77 |
12 |
75 |
58 |
|
73 |
79 |
42 |
62 |
84 |
56 |
51 |
82 |
a) Tìm phương sai và độ lệch chuẩn. Nhận xét về các kết quả nhận được.
b) Tìm giá trị bất thường.
HƯỚNG DẪN ĐÁP ÁN VÀ THANG ĐIỂM
I. PHẦN TRẮC NGHIỆM
|
Câu 1 |
A |
Câu 8 |
A |
Câu 15 |
B |
Câu 22 |
D |
Câu 29 |
D |
|
Câu 2 |
A |
Câu 9 |
A |
Câu 16 |
A |
Câu 23 |
C |
Câu 30 |
B |
|
Câu 3 |
A |
Câu 10 |
B |
Câu 17 |
B |
Câu 24 |
D |
Câu 31 |
D |
|
Câu 4 |
C |
Câu 11 |
C |
Câu 18 |
D |
Câu 25 |
C |
Câu 32 |
B |
|
Câu 5 |
A |
Câu 12 |
C |
Câu 19 |
A |
Câu 26 |
D |
Câu 33 |
C |
|
Câu 6 |
C |
Câu 13 |
C |
Câu 20 |
B |
Câu 27 |
D |
Câu 34 |
D |
|
Câu 7 |
A |
Câu 14 |
A |
Câu 21 |
C |
Câu 28 |
B |
Câu 35 |
B |
Hướng dẫn chi tiết:
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1.
Hướng dẫn giải
Đáp án đúng là A
Câu “Bạn học giỏi quá!” là câu cảm thán không xác định được tính đúng sai nên câu này không phải mệnh đề. Do đó A đúng.
Câu 2.
Hướng dẫn giải
Đáp án đúng là A
Hàm số xác định khi và chỉ khi .
Do đó tập xác định của hàm số là: D = [– 2; 2] \ {0}.
Vậy đáp án đúng là A.
Câu 3.
Hướng dẫn giải
Đáp án đúng là A
Ta có:
Khi đó A ∩ B = (2; 5].
Câu 4.
Hướng dẫn giải
Đáp án đúng là: C
Để thì m – 1 > 1 ⇔ m > 2.
Câu 5.
Hướng dẫn giải
Đáp án đúng là: A
Miền nghiệm của hệ bất phương trình là miền trong tam giác không tô màu trong hình.
Câu 6.
Hướng dẫn giải
Đáp án đúng là: C
cos113° + cos45° + cos67°
= cos(180° – 67°) + cos67° + cos45°
= – cos67° + cos67° + cos45°
= 0 +
= .
Câu 7.
Hướng dẫn giải
Đáp án đúng là: A
Áp dụng định lí sin trong tam giác ABC, ta được:
Câu 8.
Hướng dẫn giải
Đáp án đúng là: A
Áp dụng định lí cosin trong tam giác ABC ta có:
.
Câu 9.
Hướng dẫn giải
Đáp án đúng là: A
Câu 10.
Hướng dẫn giải
Đáp án đúng là: B
Câu 11.
Hướng dẫn giải
Đáp án đúng là C
Hàng của chữ số khác 0 đầu tiên của độ chính xác là hàng phần chục nghìn. Quy tròn số đến hàng phần chục nghìn ta được số gần đúng của là: 12,0964.
Câu 12.
Hướng dẫn giải
Đáp án đúng là: C
Vectơ cùng hướng với .
Câu 13.
Hướng dẫn giải
Đáp án đúng là: C
Hai vectơ cùng phương nhưng ngược hướng. Do đó C đúng và B sai.
Hai vectơ cùng hướng. Do đó D sai.
Hai vectơ không cùng phương. Do đó A sai.
Câu 14.
Hướng dẫn giải
Đáp án đúng là A
Ta có:
Hàm số bậc hai y = – 2x2 + 4x + 1 có a = – 2, b = 4, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 + 4x + 3 có a = 2, b = 4, c = 3. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 – 2x + 1 có a = 2, b = – 2, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = x2 – x + 5 có a = 1, b = –1, c = 5. Khi đó trục đối xứng là x = .
Câu 15.
Hướng dẫn giải
Đáp án đúng là: B
Áp dụng quy tắc hình bình hành ta được: .
Câu 16.
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC vuông tại A, có:
AM = BC =.
Xét tam giác ABM:
Áp dụng định lí cosin trong tam giác ABM, có:
AB2 = AM2 + BM2 – 2.AM.BM.
⇔ AB2 =
⇔ AB2 = a2
⇔ AB = a
Áp dụng định lí Pythagore trong tam giác ABC, ta được:
AC2 = BC2 – AB2 = 3a2 – a2 = 2a2
⇔ AC = a.
Vậy AB = a và AC = a.
Câu 17.
Hướng dẫn giải
Đáp án đúng là B
Hàng lớn nhất của độ chính xác là hàng phần trăm thì ta cần làm tròn đến hàng phần mười. Khi đó ta có số quy tròn của số gần đúng a là 1,2.
Câu 18.
Hướng dẫn giải
Đáp án đúng là: D
Hàm số y = ax + b nghịch biến trên ℝ khi a < 0. Do đó D đúng và A sai.
Hàm số y = – |x| vừa đồng biến và nghịch biến trên ℝ.
Hàm số y = x2 + 2x vừa đồng biến và nghịch biến trên ℝ.
Câu 19.
Hướng dẫn giải
Đáp án đúng là: A
+) Xét hàm số: f(x) = , có TXĐ: D = [ – 1; +∞).
Lấy x ∈ D và – x ∈ D
Khi đó f(– x) = ≠ f(x).
Do đó hàm số không chẵn cũng không lẻ.
+) Xét hàm số g(x) = có TXĐ D = ℝ
Lấy x ∈ D và – x ∈ D
Khi đó: g( – x) = = – g(x).
Do đó hàm số đã cho là hàm lẻ.
+) Xét hàm số h(x) = x2 – x
Lấy x ∈ D và – x ∈ D
Khi đó: h( – x) = (– x)2 – (– x) = x2 + x ≠ h(x).
Do đó hàm số đã cho là hàm không chẵn cũng không lẻ.
Vậy không có hàm số nào chẵn.
Câu 20.
Hướng dẫn giải
Đáp án đúng là B
Để hàm số y = (m – 2021)x + m – 2 đồng biến trên ℝ khi m – 2021 > 0 ⇔ m > 2021.
Vậy với m > 2021 thì hàm số đồng biến trên ℝ.
Câu 21.
Hướng dẫn giải
Đáp án đúng là C
Gọi hàm số bậc hai cần tìm là: y = ax2 + bx + c (với a, b, c ∈ ℝ, a ≠ 0)
Dựa vào bảng biến thiên ta thấy a > 0 nên đáp án D sai.
Ta có: xI = ⇔ b = – 2a. Do đó A sai.
Ta lại có: yI = ⇔ ∆ = – 8a ⇔ b2 – 4ac = – 8a ⇔ 4a2 – 4ac = – 8a ⇔ a – c = – 2 ⇔ c = a + 2
+) Nếu a = 1 thì b = – 2 và c = 3. Do đó B sai.
+) Nếu a = 2 thì b = – 4 và c = 4. Do đó C đúng.
Câu 22.
Hướng dẫn giải
Đáp án đúng là D
Câu 23.
Hướng dẫn giải
Đáp án đúng là: C
Giá trị ngoại lệ là giá trị quá nhỏ hoặc quá lớn so với các giá trị khác trong mẫu số liệu.
Câu 24.
Hướng dẫn giải
Đáp án đúng là:
Số liệu xuất hiện nhiều nhất trong mẫu số liệu được gọi là mốt của số liệu, kí hiệu là M0.
Câu 25. Hướng dẫn giải
Đáp án đúng là: C
Dựa vào bảng biến thiên ta có điểm đỉnh I có tọa độ I(– 3; 0).
Câu 26.
Hướng dẫn giải
Đáp án đúng là: D
Vì I là trung điểm của đoạn thẳng AB nên ta có: .
Câu 27.
Hướng dẫn giải
Đáp án đúng là: D
Để hàm số đã cho đồng biến trên ℝ thì 2m – 3 > 0 ⇔ m > .
Câu 28.
Hướng dẫn giải
Đáp án đúng là B
Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B mà . Do đó tam giác ABC đều
Suy ra AB = BC = AC = a.
Ta có:
.
Câu 29.
Hướng dẫn giải
Đáp án đúng là D
Câu 30.
Hướng dẫn giải
Đáp án đúng là: B
Hàm số đồng biến (đi lên) trên khoảng .
Câu 31.
Hướng dẫn giải
Đáp án đúng là: D
Ta có: 3,446 ≤ x ≤ 3,466 và 12,717 ≤ y ≤ 12,747
Khi đó chu vi C = 2(x + y) của hình chữ nhật nằm trong khoảng: 32,326 ≤ C ≤ 32,426
Suy ra 32,376 – 0,05 ≤ C ≤ 32,376 + 0,05 hay C = 32,376 ± 0,05.
Ta có độ chính xác là d = 0,05
Suy ra sai số tuyệt đối của C là: ∆C ≤ 0,05.
Câu 32.
Hướng dẫn giải
Đáp án đúng là: B
Kẻ CH vuông góc với bờ AB.
Xét tam giác ABC, có:
Vậy khoảng cách từ ngọn hải đăng tới bờ là khoảng 78 m.
Câu 33.
Hướng dẫn giải
Đáp án đúng là: C
Ta có bảng tần số sau:
|
Số con (x) |
0 |
1 |
2 |
3 |
4 |
|
Tần số (n) |
2 |
4 |
17 |
5 |
2 |
Dựa vào bảng tần số trên ta có số trung vị của dãy số liệu là trung bình cộng của số liệu thứ 15 và số liệu thứ 16 là: Q2 = .
Câu 34.
Hướng dẫn giải
Đáp án đúng là: D
Năm 2010: Diện tích lúa của Kiên Giang là 640 (hecta), của An Giang là 590 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 640 : 590 ≈ 1,08 (lần) diện tích lúa của An Giang.
Năm 2011: Diện tích lúa của Kiên Giang là 690 (hecta), của An Giang là 610 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 690 : 610 ≈ 1,13 (lần) diện tích lúa của An Giang.
Năm 2012: Diện tích lúa của Kiên Giang là 720 (hecta), của An Giang là 620 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 720 : 620 ≈ 1,16 (lần) diện tích lúa của An Giang.
Năm 2013: Diện tích lúa của Kiên Giang là 760 (hecta), của An Giang là 649 (hecta). Do đó diện tích lúa của Kiên Giang gấp: 760 : 649 ≈ 1,17 (lần) diện tích lúa của An Giang.
Câu 35.
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC, có:
II. Tự luận (3 điểm)
Bài 1 (1,0 điểm).
Hướng dẫn giải
Gọi số tiền mà doanh nghiệp A dự định giảm giá là x ( triệu đồng) (0 ≤ x ≤ 4).
Tiền lãi khi bán được một xe là: 31 – x – 27 = 4 – x (triệu đồng).
Số lượng xe bán được khi đã giảm giá là: 600 + 200x (xe).
Lợi nhuận cửa hàng thu được là: (600 + 200x)(4 – x) = – 200x2 + 200x + 2 400 (triệu đồng).
Xét hàm số bậc hai y = – 200x2 + 200x + 2 400, có:
Đỉnh I có tọa độ: xI = ; yS = .
Hay
Ta có bảng biến thiên:
Dựa vào bảng biến thiên ta thấy, hàm số đạt giá trị lớn nhất là 2 450 khi x = .
Vậy doanh nghiệp phải bán với giá 30,5 triệu đồng để lợi nhuận thu được là cao nhất.
Bài 2 (1,0 điểm).
Hướng dẫn giải
a) Gọi M là trung điểm của BC
Xét tam giác ABC, có:
Bài 3 (1,0 điểm).
Hướng dẫn giải
Ta có bảng tần số sau:
|
Điểm |
12 |
42 |
51 |
56 |
58 |
62 |
65 |
73 |
75 |
77 |
79 |
80 |
82 |
84 |
|
Tần số |
1 |
1 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
a) Số trung bình cộng:
Độ lệch chuẩn:
.
Nhận xét: Mức độ chênh lệch giữa các điểm là khá lớn.
b) Dãy số liệu có tất cả 16 số liệu, nên số trung vị là trung bình cộng của dãy số liệu ở vị trí 8 và vị trí thứ 9 ta được: .
Nửa số liệu bên trái gồm: 12; 42; 51; 51; 56; 58; 58; 62 gồm 8 giá trị. Do đó tứ phân vị thứ nhất là .
Nửa số liệu bên trái gồm: 65; 73; 75; 77; 79; 80; 82; 84 gồm 8 giá trị. Do đó tứ phân vị thứ ba là .
Suy ra khoảng tứ phân vị là: ∆Q = Q3 – Q1 = 78 – 53,5 ≈ 24,5.
Ta có: Q3 + 1,5.∆Q = 114,75 và Q1 – 1,5.∆Q = 16,75.
Ta thấy 12 < 16,75 nên 12 là giá trị ngoại lệ.
Đề thi Học kì 1 Toán lớp 10 Chân trời sáng tạo có đáp án năm 2024 - 2025 - Đề 3
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 3)
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1: Cho định lý “Hai góc đối đỉnh thì bằng nhau”. Mệnh đề nào sau đây đúng?
A. Hai góc bằng nhau là điều kiện cần và đủ để hai góc đó đối đỉnh;
B. Hai góc đối đỉnh là điều kiện cần để hai góc đó bằng nhau;
C. Hai góc bằng nhau là điều kiện đủ để hai góc đó đối đỉnh;
D. Hai góc đối đỉnh là điều kiện đủ để hai góc đó bằng nhau.
Câu 2: Cho tập hợp A = {x ∈ ℝ| – 1 ≤ x < 3}. Xác định phần bù của tập hợp A trong ℝ.
A. ;
B. ;
C. ;
D. .
Câu 3: Hệ nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
Câu 4: Một bệnh viện thống kê số ca nhập viện do tai nạn giao thông mỗi ngày trong tháng 9/2020 ở bảng sau:
|
Số ca |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
12 |
15 |
|
Số ngày |
2 |
3 |
4 |
6 |
3 |
2 |
2 |
3 |
2 |
1 |
1 |
1 |
Khoảng tứ phân vị của dãy số liệu trên là:
A. 3,5;
B. 2;
C. 5;
D. 7.
Câu 5: Cho hàm số y = x2 – 2x – 2 có đồ thị là parabol (P) và đường thẳng (d) có phương trình y = x + m. Giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B sao cho OA2 + OB2 đạt giá trị nhỏ nhất là:
A. ;
B. ;
C. m = 1;
D. m = 2.
Câu 6: Hà ghi lại số liệu từ trang web của Tổng cục thống kê bảng dân số Việt Nam qua các năm từ 2015 đến 2020:
|
Năm |
Số dân |
|
2015 |
92 677 076 |
|
2016 |
93 640, 422 |
|
2017 |
94 600 648 |
|
2018 |
95 545 962 |
|
2019 |
96 462 106 |
|
2020 |
97 338 579 |
Bạn Hà đã ghi nhầm dân số của năm nào?
A. 2015;
B. 2016;
C. 2019;
D. 2020.
Câu 7: Hàm số nào dưới đây là hàm số không chẵn cũng không lẻ?
A. y = – 2|x – 1|;
B. y = x3 – 5x;
C. ;
D. y = – x.
Câu 8: Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
A. y = – 2x2 + 4x + 1;
B. y = 2x2 + 4x + 3;
C. y = 2x2 – 2x + 1;
D. y = x2 – x + 5.
Câu 9: Tập xác định D của hàm số là
A. D = [– 2; 2] \ {0};
B. D = [– 2; 2];
C. D = (– 2; 2);
D. D = ℝ.
Câu 10: Cho hàm số y = (m – 2021)x + m – 2. Điều kiện để hàm số đồng biến trên ℝ là
A. m < 2021;
B. m > 2021;
C. 2 < m < 2021;
D. m ≥ 2021.
Câu 11: Cho , với 0° < α < 90°. Giá trị của cosα bằng:
Câu 12: Tính giá trị biểu thức sau: sin12° + sin178° + cos106° + cos74°
A. 2sin12°;
B. 2cos74°;
C. cos74°;
D. sin12°.
Câu 13: Cho tam giác ABC có AB = 2, và . Độ dài cạnh AC là:
A. 2,55;
B. 3,10;
C. 1,57;
D. 1,29.
Câu 14: Cho bảng biến thiên sau:
Đồ thị hàm số bậc hai tương ứng với bảng biến thiên trên là :
A. y = x2 + 2x – 1;
B. y = x2 – 2x + 2;
C. y = 2x2 – 4x + 4;
D. y = – 3x2 + 6x – 1.
Câu 15: Phát biểu nào sau đây là sai?
A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
B. Vectơ là đoạn thẳng có hướng.
C. Hai vectơ cùng hướng thì cùng phương.
D. Hai vectơ cùng phương thì cùng hướng.
Câu 16: Cho hình vuông ABCD. Hãy chọn khẳng định đúng.
Câu 17: Cho hình vẽ sau:
Trong các vectơ trên hình, có bao nhiêu vectơ cùng phương với vectơ ?
A. 3;
B. 5;
C. 6;
D. 7.
Câu 18: Để lắp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 9 km, rồi nối từ vị trí C đến B dài 12km. Biết góc tạo bởi 2 đoạn dây AC và CB là 52°. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?
A. 9,6;
B. 11,4;
C. 92,0;
D. 71,0.
Câu 19: Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Chọn khẳng định đúng trong các khẳng định sau:
Câu 20: Cho hình bình hành ABCD. Biểu thức bằng:
A. ;
B. ;
C. ;
D. .
Câu 21: Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ bằng:
A. 1;
B. 6;
C. ;
D. 3.
Câu 22: Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
A. 12,096;
B. 12,09638;
C. 12,0964;
D. 12,10.
Câu 23: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Đặt , . Hãy phân tích vectơ theo 2 vectơ và :
Câu 24: Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
A. 1,24;
B. 1,2;
C. 1,236;
D. 1.
Câu 25: Cho hình thoi ABCD có cạnh bằng 4. . Tính :
A. 8;
B. 16;
C. 24;
D. 32.
Câu 26: Cho hình thang vuông ABCD có . Tính :
A. 0;
B. ;
C. ;
D. 1.
Câu 27: Cho mẩu tin sau:
Trong tháng 01/2021 có 47 dự án được cấp phép mới với số vốn đăng kí đạt gần 1,3 tỉ USD, giảm khoảng 81,8% về số dự án và 70,3% về số vốn đăng kí so với cùng kì năm trước; 46 lượt dự án đã cấp phép từ các năm trước đăng kí điều chỉnh vốn đầu tư với số vốn tăng thêm trên 0,5 tỉ USD, tăng gần 41,4%.
Trong các số liệu đã cho trong bài, số số gần đúng là:
A. 2;
B. 3;
C. 4;
D. 5.
Câu 28: Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ bằng
A. a;
B. ;
C. ;
D. .
Câu 29: Lớp 10A có 40 học sinh. Tỉ lệ số lượng mỗi loại học lực của học sinh lớp 10A được biểu diễn bằng biểu đồ sau:
Hỏi số lượng học sinh khá của lớp 10A là:
A. 1;
B. 2;
C. 15;
D. 22.
Câu 30: Một xạ thủ bắn súng 10 lần liên tiếp, số điểm của xạ thủ đạt được được ghi lại trong bảng sau:
|
Số lần |
Lần 1 |
Lần 2 |
Lần 3 |
Lần 4 |
Lần 5 |
Lần 6 |
Lần 7 |
Lần 8 |
Lần 9 |
Lần 10 |
|
Số điểm |
8 |
6 |
7 |
6 |
9 |
8 |
10 |
7 |
7 |
8 |
Số trung vị của số liệu trên là:
A. 6,5;
B. 7;
C. 8;
D. 7,5.
Câu 31: Thực hiện đo chiều cao (đơn vị cm) của các bạn học sinh tổ 1 của lớp 10D và được ghi lại như sau: 154; 172; 164; 145; 160; 151; 152; 181. Chiều cao trung bình của các bạn tổ 1 là:
A. 155;
B. 160;
C. 170;
D. 150.
Câu 32: Số huy chương vàng trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam trong các giải đấu ở châu Á trong các năm từ 2010 đến 2019 được thống kê trong bảng sau:
|
Năm |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
Số huy chương |
39 |
43 |
115 |
52 |
56 |
62 |
130 |
82 |
74 |
120 |
Độ lệch chuẩn của số liệu trên là:
A. 77,3;
B. 1002,61;
C. 31,664;
D. 91.
Câu 33: Máy bay A bay với vận tốc , máy bay B bay cùng hướng và có tốc độ chỉ bằng một nửa máy bay A. Biểu diễn vectơ vận tốc của máy bay B theo vectơ vận tốc của máy bay A là:
A. ;
B. ;
C. ;
D. .
Câu 34: Khoảng đồng biến và nghịch biến của hàm số y = là:
A. (– ∞; –1) và (–1; + ∞);
B. ℝ\{– 1};
C. (– ∞; –1);
D. (–1; + ∞).
Câu 35: Tứ giác ABCD có . Khi đó tứ giác ABCD là hình:
A. hình thang;
B. hình bình hành;
C. hình vuông;
D. hình chữ nhật.
II. PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 1 (1 điểm).
Cho hình chữ nhật ABCD, M là một điểm bất kì. Chứng minh: .
Câu 2 (0,5 điểm). Cho tam giác ABC có và --> Gọi I là điểm thỏa mãn Tính độ dài đoạn thẳng AI
Câu 3 (1 điểm). Cổng chào Yên Lạc có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng (tính từ mặt đất đến điểm cao nhất của cổng).
Câu 4 (0,5 điểm). Nam đo được đường kính của một hình tròn là 24 ± 0,2 cm. Nam tính được chu vi đường tròn là C = 75,36. Hãy ước lượng sai số tuyệt đối của C, biết 3,141 < π < 3,142.
HƯỚNG DẪN ĐÁP ÁN VÀ THANG ĐIỂM
I. PHẦN TRẮC NGHIỆM
|
Câu 1 |
D |
Câu 8 |
A |
Câu 15 |
D |
Câu 22 |
C |
Câu 29 |
C |
|
Câu 2 |
B |
Câu 9 |
A |
Câu 16 |
B |
Câu 23 |
D |
Câu 30 |
D |
|
Câu 3 |
B |
Câu 10 |
B |
Câu 17 |
D |
Câu 24 |
B |
Câu 31 |
B |
|
Câu 4 |
C |
Câu 11 |
C |
Câu 18 |
A |
Câu 25 |
C |
Câu 32 |
C |
|
Câu 5 |
A |
Câu 12 |
A |
Câu 19 |
B |
Câu 26 |
A |
Câu 33 |
A |
|
Câu 6 |
B |
Câu 13 |
A |
Câu 20 |
A |
Câu 27 |
D |
Câu 34 |
A |
|
Câu 7 |
A |
Câu 14 |
C |
Câu 21 |
D |
Câu 28 |
B |
Câu 35 |
A |
Hướng dẫn chi tiết:
Câu 1: Cho định lý “Hai góc đối đỉnh thì bằng nhau”. Mệnh đề nào sau đây đúng?
A. Hai góc bằng nhau là điều kiện cần và đủ để hai góc đó đối đỉnh;
B. Hai góc đối đỉnh là điều kiện cần để hai góc đó bằng nhau;
C. Hai góc bằng nhau là điều kiện đủ để hai góc đó đối đỉnh;
D. Hai góc đối đỉnh là điều kiện đủ để hai góc đó bằng nhau.
Hướng dẫn giải
Đáp án đúng là D
Từ định lý “Hai góc đối đỉnh thì bằng nhau”, ta có thể phát biểu lại định lí này như sau:
Hai góc đối đỉnh là điều kiện đủ để hai góc đó bằng nhau. Do đó D đúng và B sai.
Hai góc bằng nhau là điều kiện cần để hai góc đó đối đỉnh. Do đó C sai.
Vì hai góc bằng nhau nhưng chưa chắc đối đỉnh do đó đáp án A là sai.
Câu 2: Cho tập hợp A = {x ∈ ℝ| – 1 ≤ x < 3}. Xác định phần bù của tập hợp A trong ℝ.
Hướng dẫn giải
Đáp án đúng là B
Ta có: A = {x ∈ ℝ| – 1 ≤ x < 3} = [ – 1; 3)
Khi đó ℝ \ A = ℝ \ [ – 1; 3) = (– ∞; – 1) ∪ [3; + ∞).
Câu 3: Hệ nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
Hướng dẫn giải
Đáp án đúng là B
Hệ bất phương trình bậc nhất hai ẩn là hệ gồm các bất phương trình bậc nhất hai ẩn. Do đó đáp án B là đúng.
Câu 4: Một bệnh viện thống kê số ca nhập viện do tai nạn giao thông mỗi ngày trong tháng 9/2020 ở bảng sau:
|
Số ca |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
12 |
15 |
|
Số ngày |
2 |
3 |
4 |
6 |
3 |
2 |
2 |
3 |
2 |
1 |
1 |
1 |
Khoảng tứ phân vị của dãy số liệu trên là:
A. 3,5;
B. 2;
C. 5;
D. 7.
Hướng dẫn giải
Đáp án đúng là C
Dãy số liệu trên có 30 số liệu.
Số trung vị của dãy số liệu là số trung bình cộng của số liệu ở vị trí thứ 15 và 16: Q2 = .
Số trung vị của nửa số liệu bên trái là: Q1 = 2.
Số trung vị của nửa số liệu bên phải là: Q2 = 7.
Khoảng tứ phân vị ∆Q = Q2 – Q1 = 7 – 2 = 5.
Câu 5: Cho hàm số y = x2 – 2x – 2 có đồ thị là parabol (P) và đường thẳng (d) có phương trình y = x + m. Giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B sao cho OA2 + OB2 đạt giá trị nhỏ nhất là:
A. ;
B. ;
C. m = 1;
D. m = 2.
Hướng dẫn giải
Đáp án đúng là A
Xét phương trình hoành độ giao điểm:
x2 – 2x – 2 = x + m (1)
⇔ x2 – 3x – 2 – m = 0
Ta có: ∆ = (– 3)2 – 4.1.(– 2 – m) = 17 + 4m
Để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B thì phương trình (1) có hai nghiệm phân biệt ⇔ ∆ = 17 + 4m > 0 ⇔ m > >>.
Gọi x1 và x2 là nghiệm của phương trình (1).
Áp dụng định lí Vi – et ta được: .
Đặt A(x1; y1) và B(x2; y2)
Vậy OA2 + OB2 đạt giá trị nhỏ nhất bằng khi m = .
Câu 6: Hà ghi lại số liệu từ trang web của Tổng cục thống kê bảng dân số Việt Nam qua các năm từ 2015 đến 2020:
|
Năm |
Số dân |
|
2015 |
92 677 076 |
|
2016 |
93 640, 422 |
|
2017 |
94 600 648 |
|
2018 |
95 545 962 |
|
2019 |
96 462 106 |
|
2020 |
97 338 579 |
Bạn Hà đã ghi nhầm dân số của năm nào?
A. 2015;
B. 2016;
C. 2019;
D. 2020.
Hướng dẫn giải
Đáp án đúng là B
Dân số Việt Nam năm 2016 là 93 640 422 (người). Do đó bạn Hà ghi sai số liệu năm 2016.
Câu 7: Hàm số nào dưới đây là hàm số không chẵn cũng không lẻ?
A. y = – 2|x – 1|;
B. y = x3 – 5x;
C. ;
D. y = – x.
Hướng dẫn giải
Đáp án đúng là A
Tập xác định của các hàm số đã cho là D = ℝ
Lấy x ∈ D khi đó – x ∈ D, ta có:
+) y(– x) = – 2|(– x) – 1| = – 2|x + 1| ≠ y(x).
Do đó hàm số không chẵn cũng không lẻ.
+) y(– x) = (– x)3 – 5(– x) = - x3 + 5x = - (x3 – 5x) = – y(x).
Do đó hàm số là hàm số lẻ.
+) .
Do đó hàm số là hàm số chẵn.
+) y(– x) = – (– x) = x = – y(x).
Do đó hàm số là hàm lẻ.
Câu 8: Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
A. y = – 2x2 + 4x + 1;
B. y = 2x2 + 4x + 3;
C. y = 2x2 – 2x + 1;
D. y = x2 – x + 5.
Hướng dẫn giải
Đáp án đúng là A
Ta có:
Hàm số bậc hai y = – 2x2 + 4x + 1 có a = – 2, b = 4, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 + 4x + 3 có a = 2, b = 4, c = 3. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 – 2x + 1 có a = 2, b = – 2, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = x2 – x + 5 có a = 1, b = –1, c = 5. Khi đó trục đối xứng là x = .
Câu 9: Tập xác định D của hàm số là
A. D = [– 2; 2] \ {0};
B. D = [– 2; 2];
C. D = (– 2; 2);
D. D = ℝ.
Hướng dẫn giải
Đáp án đúng là A
Hàm số xác định khi và chỉ khi .
Do đó tập xác định của hàm số là: D = [– 2; 2] \ {0}.
Vậy đáp án đúng là A.
Câu 10: Cho hàm số y = (m – 2021)x + m – 2. Điều kiện để hàm số đồng biến trên ℝ là
A. m < 2021;
B. m > 2021;
C. 2 < m < 2021;
D. m ≥ 2021.
Hướng dẫn giải
Đáp án đúng là B
Để hàm số y = (m – 2021)x + m – 2 đồng biến trên ℝ khi m – 2021 > 0 ⇔ m > 2021.
Vậy với m > 2021 thì hàm số đồng biến trên ℝ.
Câu 11: Cho , với 0° < α < 90°. Giá trị của cosα bằng:
Hướng dẫn giải
Đáp án đúng là C
Ta có: tan2α + 1 =
⇔ cos2α =
⇔ cos2α =
⇔ cosα = (0° < α < 90°).
Vậy chọn đáp án C
Câu 12: Tính giá trị biểu thức sau: sin12° + sin178° + cos106° + cos74°
A. 2sin12°;
B. 2cos74°;
C. cos74°;
D. sin12°.
Hướng dẫn giải
Đáp án đúng là A
sin12° + sin178° + cos106° + cos74°
= sin12° + sin(180° – 12°) + cos(180° – 74°) + cos74°
= sin12° + sin12° – cos74° + cos74°
= 2.sin12°.
Câu 13: Cho tam giác ABC có AB = 2, và . Độ dài cạnh AC là:
A. 2,55;
B. 3,10;
C. 1,57;
D. 1,29.
Hướng dẫn giải
Đáp án đúng là A
Xét tam giác ABC, có: (định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC, ta được:
Câu 14: Cho bảng biến thiên sau:
Đồ thị hàm số bậc hai tương ứng với bảng biến thiên trên là :
A. y = x2 + 2x – 1;
B. y = x2 – 2x + 2;
C. y = 2x2 – 4x + 4;
D. y = – 3x2 + 6x – 1.
Hướng dẫn giải
Đáp án đúng là C
Gọi hàm số bậc hai cần tìm là: y = ax2 + bx + c (với a, b, c ∈ ℝ, a ≠ 0)
Dựa vào bảng biến thiên ta thấy a > 0 nên đáp án D sai.
Ta có: xI = ⇔ b = – 2a. Do đó A sai.
Ta lại có: yI = ⇔ ∆ = – 8a ⇔ b2 – 4ac = – 8a ⇔ 4a2 – 4ac = – 8a ⇔ a – c = – 2 ⇔ c = a + 2
+) Nếu a = 1 thì b = – 2 và c = 3. Do đó B sai.
+) Nếu a = 2 thì b = – 4 và c = 4. Do đó C đúng.
Câu 15: Phát biểu nào sau đây là sai?
A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
B. Vectơ là đoạn thẳng có hướng.
C. Hai vectơ cùng hướng thì cùng phương.
D. Hai vectơ cùng phương thì cùng hướng.
Hướng dẫn giải
Đáp án đúng là D
Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng. Do đó D là phát biểu sai.
Câu 16: Cho hình vuông ABCD. Hãy chọn khẳng định đúng.
Hướng dẫn giải
Đáp án đúng là B
Ta có: là hai vectơ không cùng phương dù chúng có cùng độ dài. Suy ra . Do đó A sai.
Ta có: (quy tắc hình bình hành). Do đó B đúng.
Nếu độ dài cạnh của hình vuông là a thì = a và . Suy ra . Do đó C sai.
Hai vectơ và cùng phương cùng độ dài nhưng ngược hướng. Suy ra . Do đó D sai.
Câu 17: Cho hình vẽ sau:
Trong các vectơ trên hình, có bao nhiêu vectơ cùng phương với vectơ ?
A. 3;
B. 5;
C. 6;
D. 7.
Hướng dẫn giải
Đáp án đúng là D
Hai vec tơ cùng phương là hai vectơ có giá song song hoặc trùng nhau. Khi đó các vectơ cùng phương với vectơ là .
Vậy có tất cả 7 vectơ cùng phương với vectơ .
Câu 18: Để lắp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 9 km, rồi nối từ vị trí C đến B dài 12km. Biết góc tạo bởi 2 đoạn dây AC và CB là 52°. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?
A. 9,6;
B. 11,4;
C. 92,0;
D. 71,0.
Hướng dẫn giải
Đáp án đúng là A
Áp dụng định lí cos vào tam giác ABC ta được:
AB2 = AC2 + CB2 – 2.AC.CB.cos52°
= 92 + 122 – 2.9.12.cos52°
≈ 92,0
⇔ AB ≈ 9,6 m.
So với việc nối thẳng từ A đến B phải tốn thêm số mét dây là: 9 + 12 – 9,6 ≈ 11,4 (m).
Câu 19: Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Chọn khẳng định đúng trong các khẳng định sau:
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là B
+) Ta có: và là hai vectơ cùng phương cùng độ dài nhưng ngược hướng. Do đó . Suy ra A sai.
+) Xét tam giác ABC, có:
O là trung điểm của AC
N là trung điểm của BC
Suy ra ON là đường trung bình của tam giác ABC
Khi đó ON // AB và ON = AB = AM = MB.
Do đó . Suy ra B đúng.
+) Ta có: và là hai vectơ có cùng độ dài nhưng không cùng hướng. Do đó . Suy ra C sai.
+) Ta có: và là hai vectơ không cùng độ dài và không cùng hướng. Do đó . Suy ra D sai.
Câu 20: Cho hình bình hành ABCD. Biểu thức bằng:
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là A
Ta có:
Câu 21: Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ bằng:
A. 1;
B. 6;
C. ;
D. 3.
Hướng dẫn giải
Đáp án đúng là D
Vì ABC là tam giác đều nên O là trọng tâm tam giác ABC. Khi đó
Ta có:
Ta lại có: M là điểm nằm trên đường tròn nên MO = 1.
.
Câu 22: Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
A. 12,096;
B. 12,09638;
C. 12,0964;
D. 12,10.
Hướng dẫn giải
Đáp án đúng là C
Hàng của chữ số khác 0 đầu tiên của độ chính xác là hàng phần chục nghìn. Quy tròn số đến hàng phần chục nghìn ta được số gần đúng của là: 12,0964.
Câu 23: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Đặt , . Hãy phân tích vectơ theo 2 vectơ và :
Hướng dẫn giải
Đáp án đúng là D
Câu 24: Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
A. 1,24;
B. 1,2;
C. 1,236;
D. 1.
Hướng dẫn giải
Đáp án đúng là B
Hàng lớn nhất của độ chính xác là hàng phần trăm thì ta cần làm tròn đến hàng phần mười. Khi đó ta có số quy tròn của số gần đúng a là 1,2.
Câu 25: Cho hình thoi ABCD có cạnh bằng 4. . Tính :
A. 8;
B. 16;
C. 24;
D. 32.
Hướng dẫn giải
Đáp án đúng là C
Ta có hình vẽ sau:
Vì ABCD là hình thoi nên AC ⊥ BD tại O
⇒ (tính chất hình thoi)
Xét tam giác ABC vuông tại O, có:
AO = sin.AB = sin60°.4 = .
⇒ AC = 2.AO = 2.= .
Ta có:
Khi đó: .
Câu 26: Cho hình thang vuông ABCD có . Tính :
A. 0;
B.;
C. ;
D. 1.
Câu 27: Cho mẩu tin sau:
Trong tháng 01/2021 có 47 dự án được cấp phép mới với số vốn đăng kí đạt gần 1,3 tỉ USD, giảm khoảng 81,8% về số dự án và 70,3% về số vốn đăng kí so với cùng kì năm trước; 46 lượt dự án đã cấp phép từ các năm trước đăng kí điều chỉnh vốn đầu tư với số vốn tăng thêm trên 0,5 tỉ USD, tăng gần 41,4%.
Trong các số liệu đã cho trong bài, số số gần đúng là:
A. 2;
B. 3;
C. 4;
D. 5.
Hướng dẫn giải
Đáp án đúng là D
Trong các số liệu đã cho trong bài, ta có:
- Các số đúng là: 47; 46.
- Các số gần đúng là: 1,3; 81,8%; 70,3%; 0,5; 41,4%.
Vậy có 5 số số gần đúng.
Câu 28: Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ bằng
A. a;
B. ;
C.;
D. .
Hướng dẫn giải
Đáp án đúng là B
Ta có:
Khi đó .
Câu 29: Lớp 10A có 40 học sinh. Tỉ lệ số lượng mỗi loại học lực của học sinh lớp 10A được biểu diễn bằng biểu đồ sau:
Hỏi số lượng học sinh khá của lớp 10A là:
A. 1;
B. 2;
C. 15;
D. 22.
Hướng dẫn giải
Đáp án đúng là C
Tỉ lệ học sinh khá trong lớp 10A là 37,5% nên số học sinh đạt học lực khá của lớp 10A là:
37,5%.40 = 15 (học sinh)
Vậy lớp 10A có 15 học sinh đạt học lực khá.
Câu 30: Một xạ thủ bắn súng 10 lần liên tiếp, số điểm của xạ thủ đạt được được ghi lại trong bảng sau:
|
Số lần |
Lần 1 |
Lần 2 |
Lần 3 |
Lần 4 |
Lần 5 |
Lần 6 |
Lần 7 |
Lần 8 |
Lần 9 |
Lần 10 |
|
Số điểm |
8 |
6 |
7 |
6 |
9 |
8 |
10 |
7 |
7 |
8 |
Số trung vị của số liệu trên là:
A. 6,5;
B. 7;
C. 8;
D. 7,5.
Hướng dẫn giải
Đáp án đúng là D
Sắp xếp dãy số liệu theo thứ tự không giảm ta được: 6; 6; 7; 7; 7; 8; 8; 8; 9; 10.
Dãy số liệu trên có 10 số liệu nên số trung vị là trung bình cộng của số liệu thứ 5 và 6: Q2 = .
Câu 31: Thực hiện đo chiều cao (đơn vị cm) của các bạn học sinh tổ 1 của lớp 10D và được ghi lại như sau: 154; 172; 164; 145; 160; 151; 152; 181. Chiều cao trung bình của các bạn tổ 1 là:
A. 155;
B. 160;
C. 170;
D. 150.
Hướng dẫn giải
Đáp án đúng là B
Chiều cao trung bình của tổ 1 là:
Câu 32: Số huy chương vàng trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam trong các giải đấu ở châu Á trong các năm từ 2010 đến 2019 được thống kê trong bảng sau:
|
Năm |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
Số huy chương |
39 |
43 |
115 |
52 |
56 |
62 |
130 |
82 |
74 |
120 |
Độ lệch chuẩn của số liệu trên là:
A. 77,3;
B. 1002,61;
C. 31,664;
D. 91.
Hướng dẫn giải
Đáp án đúng là C
Số trung bình của số liệu trên là:
Câu 33: Máy bay A bay với vận tốc , máy bay B bay cùng hướng và có tốc độ chỉ bằng một nửa máy bay A. Biểu diễn vectơ vận tốc của máy bay B theo vectơ vận tốc của máy bay A là:
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là A
Vì vectơ vận tốc của máy bay B cùng hướng theo vectơ vận tốc của máy bay A và có độ lớn bằng một nửa vectơ nên .
Câu 34: Khoảng đồng biến và nghịch biến của hàm số y = là:
A. (– ∞; –1) và (–1; + ∞);
B. ℝ\{– 1};
C. (– ∞; –1);
D. (–1; + ∞).
Hướng dẫn giải
Đáp án đúng là A
Tập xác định D = ℝ\{– 1}
Lấy x1, x2 là hai số tùy ý thuộc (– ∞; –1) và (–1; + ∞) sao cho x1 < x2 ta có:
+) Nếu x1, x2 ∈ (– ∞; –1) thì x1 + 1, x2 + 1 < 0 mà x2 – x1 > 0
Suy ra nên f(x1) > f(x2).
Do đó hàm số đã đồng biến trên (– ∞; –1).
+) Nếu x1, x2 ∈ (–1; + ∞) thì x1 + 1, x2 + 1 > 0 mà x2 – x1 > 0
Suy ra nên f(x1) > f(x2).
Do đó hàm số đã đồng biến trên (–1; + ∞).
Vậy hàm số đồng biến trên các khoảng (– ∞; –1) và (–1; + ∞).
Câu 35: Tứ giác ABCD có . Khi đó tứ giác ABCD là hình:
A. hình thang;
B. hình bình hành;
C. hình vuông;
D. hình chữ nhật.
Hướng dẫn giải
Đáp án đúng là A
Ta có:
⇔
⇔
Do đó và cùng phương nên AB // CD
Vì vậy ABCD là hình thang.
II. PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 1 (1 điểm).
Cho hình chữ nhật ABCD, M là một điểm bất kì. Chứng minh: .
Hướng dẫn giải
Đáp án đúng là
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC và BD. Do đó: và
Ta có:
Câu 2 (0,5 điểm). Cho tam giác ABC có và Gọi I là điểm thỏa mãn Tính độ dài đoạn thẳng AI
Hướng dẫn giải
Xét tam giác ABC, có:
nên I thuộc vào đoạn thẳng BC và thỏa mãn IC = 2IB.
Áp dụng định lí cos trong tam giác ABC, ta được:
BC2 = AB2 + AC2 – 2AB.AC.cosA =
⇒ BC = a
⇒ AB = BC = a
⇒ Tam giác ABC cân tại B
⇒
Ta lại có IC = 2IB nên IC = , IB =
Xét tam giác IAC có:
Áp dụng định lí cos, ta được:
IA2 = AC2 + IC2 – 2.AC.IC.cos
=
⇔ IA = .
Vậy IA = .
Câu 3 (1 điểm). Cổng chào Yên Lạc có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng (tính từ mặt đất đến điểm cao nhất của cổng).
Hướng dẫn giải
Vì cổng có hình dạng parabol nên có phương trình y = ax2 + bx + c (a ≠ 0) (1)
Đặt hệ trục tọa độ như hình vẽ:
Ta có: A(– 81; 0) và B(81; 0) và M(– 71; 43)
Thay lần lượt tọa độ các điểm vào (1) ta được:
0 = a.(– 81)2 + b(– 81) + c ⇔ 6 561a – 81b + c = 0 (2)
0 = a.812 + b.81 + c ⇔ 6 561a + 81b + c = 0 (3)
43 = a.(– 71)2 + b(– 71) + c ⇔ 5 041 a – 71b + c = 43 (4)
Lấy vế với vế của phương trình (2) trừ (3) ta được: – 162b = 0 ⇔ b = 0.
Khi đó:
(2) ⇔ 6 561a + c = 0
(4) ⇔ 5 041 a + c = 43
Từ đó ta có hệ phương trình:
Suy ra ta có phương trình: y = – 0,03x2 + 185,6.
Điểm H thuộc vào trục Oy nên xH = 0 ⇒ yH = – 0,03.02 + 185,6 = 185,6.
Vì vậy chiều cao của cổng chính là đoạn OH và bằng 185,6 m.
Câu 4 (0,5 điểm). Nam đo được đường kính của một hình tròn là 24 ± 0,2 cm. Nam tính được chu vi đường tròn là C = 75,36. Hãy ước lượng sai số tuyệt đối của C, biết 3,141 < π < 3,142.
Hướng dẫn giải
Gọi và lần lượt là đường kính và chu vi của đường tròn.
Ta có: 24 – 0,2 ≤ ≤ 24 + 0,2 hay 23,8 ≤ ≤ 24,2
Suy ra 3,141.23,8 ≤ .π ≤ 24,2.3,42 ⇔ 74,7558 ≤ ≤ 76,0364
⇔ 74,7558 – 75,36 ≤ – 75,36 ≤ 76,0364 – 75,36
⇔ – 0,6042 ≤ – 75,36 ≤ 0,6764.
Vậy sai số tuyệt đối của C nằm trong khoảng từ – 0,6042 đển 0,6764.
Đề thi Học kì 1 Toán lớp 10 Chân trời sáng tạo có đáp án năm 2024 - 2025 - Đề 4
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 4)
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
Câu 1: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?
a) Huế là một thành phố của Việt Nam.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Hãy trả lời câu hỏi này!
d)
e)
f) Bạn có mang theo máy tính không?
g)
A. 1. B. 2. C. 3. D. 4.
Câu 2: Hãy viết số quy tròn của số gần đúng biết
A. 17700. B. 17800. C. 17500. D. 17600.
Câu 3: Cho hình bình hành có là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai?
A. B.
C. D.
Câu 4: Lớp 10E có học sinh giỏi Toán, học sinh giỏi Lý, học sinh giỏi Hóa, học sinh giỏi cả Toán và Lý, học sinh giỏi cả Toán và Hóa, học sinh giỏi cả Lý và Hóa, học sinh giỏi cả môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10E là
A. B. C. D.
Câu 5: Miền nghiệm của bất phương trình: là nửa mặt phẳng chứa điểm:
A. B. C. D.
Câu 6: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
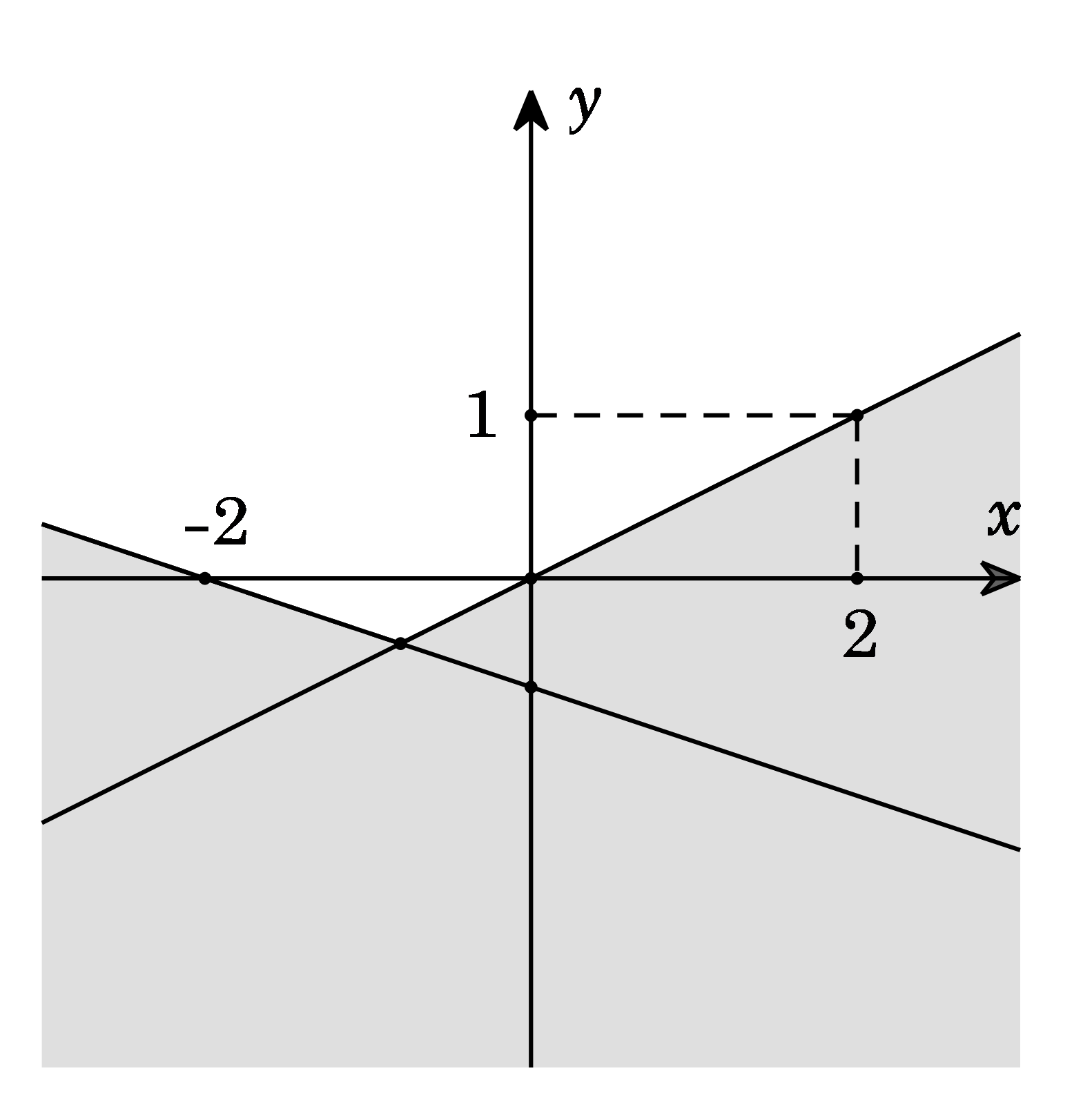
A. B. C. D.
Câu 7: Tam giác có và . Tính bán kính của đường tròn ngoại tiếp tam giác .
A. . B. . C. . D. .
Câu 8: Hai chiếc tàu thủy cùng xuất phát từ một vị trí , đi thẳng theo hai hướng tạo với nhau góc . Tàu chạy với tốc độ hải lí một giờ. Tàu chạy với tốc độ hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
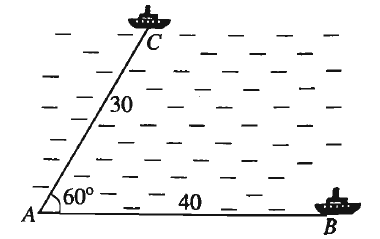
Kết quả gần nhất với số nào sau đây?
A. hải lí.
B. hải lí.
C. hải lí.
D. hải lí.
Câu 9: Tính giá trị biểu thức .
A. B. C. D.
Câu 10: Cho hình vuông cạnh . Tính
A. B. C. D.
Câu 11: Tìm tập xác định của hàm số
A. B. C. D.
Câu 12: Cho hàm số . Điểm nào sau đây thuộc đồ thị hàm số:
A. . B. . C. . D. .
Câu 13: Gọi là trọng tâm của . Đặt . Xác định giá trị của để .
A. B. C. D.
Câu 14: Tam giác có . Tính diện tích tam giác .
A. . B. . C. . D. .
Câu 15: Hàm số , đồng biến trong khoảng nào sau đậy?
A. B. C. D.
Câu 16: Sản lượng lúa của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng tần số sau đây: (đơn vị: tạ)

Độ lệch chuẩn là
A. 1,24 B. 1,54 C. 22,1 D. 4,70
Câu 17: Cho tập hợp là ước chung của . Hãy liệt kê các phần tử của tập hợp .
A. B.
C. D.
Câu 18: Cho hai tập hợp Mệnh đề nào sau đây đúng?
A. B. C. D.
Câu 19: Điểm thuộc miền nghiệm của hệ bất phương trìnhnào sau đây?
A. B.
C. D.
Câu 20: Giá trị nhỏ nhất của biểu thức trên miền xác định bởi hệ là
A. B. C. D.
Câu 21: Hàm số bậc hai nào sau đây có đồ thị là parabol có hoành độ đỉnh là và đi qua ?
A. . B. .
C. . D. .
Câu 22: Cho biết Giá trị của bằng bao nhiêu?
A. B. C. D.
Câu 23: Cho tam giác ABC. Trên cạnh BC lấy điểm sao cho . Khi đó, vectơ bằng
A. B. C. D.
Câu 24: Cho hai vecto bất kỳ; . Khẳng định nào sau đây không đúng?
A. B. C. D.
Câu 25: Tam giác vuông tại có cm, cm. Tính bán kính của đường tròn nội tiếp tam giác đã cho.
A. cm. B. cm. C. cm. D. cm.
Câu 26: Một miếng đất hình chữ nhật có chiều rộng và chiều dài . Tính chu vi của miếng đất đã cho.
A. B.
C. D.
Câu 27: Khoảng biến thiên của mẫu số liệu 1 1 1 2 2 2 3 3 4 20 là:
A. 1. B. 3,9. C. 19. D. 20.
Câu 28: Cho parabol có đồ thị như hình sau
Phương trình của parabol này là
A. . B. . C. . D. .
Câu 29: Bảng biến thiên của hàm số là:
A.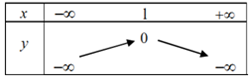 B.
B. 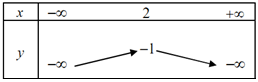
C. 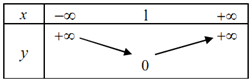 D.
D. 
Câu 30: Cho tam giác đều có cạnh bằng Tính tích vô hướng
A. B. C. D.
Phần 2: Tự luận (3 điểm)
Câu 1: Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được
cho ở bảng sau:
|
Ngày |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Nhiệt độ |
23 |
25 |
26 |
27 |
27 |
27 |
27 |
21 |
19 |
18 |
(Nguồn: https://nchmf.gov.vn)
a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.
b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.
Câu 2: Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn
a)
b)
c)
Câu 3: Tìm parabol (P) biết (P) có đỉnh và giao với Oy tại điểm có tung độ bằng -1. Vẽ đồ thị hàm số tìm được.
----- HẾT -----
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (30 câu – 6 điểm)
|
1.B |
2.D |
3.C |
4.B |
5.C |
6.C |
7.C |
8.B |
9.B |
10.D |
|
11.A |
12.A |
13.A |
14.B |
15.C |
16.B |
17.C |
18.A |
19.C |
20.C |
|
21.D |
22.D |
23.A |
24.D |
25.A |
26.C |
27.A |
28.C |
29.B |
30.C |
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
a) Mẫu số liệu thống kê nhiệt độ nhận được từ bảng là:
23 25 26 27 27 27 27 21 19 18
b)
* Nhiệt độ trung bình của 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 là:
()
* Phương sai
* Độ lệch chuẩn
Câu 2 (VD):
a) Gọi I là trung điểm ta có:
Vậy tập hợp điểm là đường tròn tâm , bán kính .
b) Gọi là điểm thoả mān:
L là điểm thoả mān:
Ta có:
Tập hợp điểm là đường trung trực của đoạn thẳng .
c) Với I là trung điểm của . Gọi là điểm thoả mān:
Ta có:
const
Vậy tập hợp điểm là đường tròn tâm bán kính .
Câu 3 (VD):
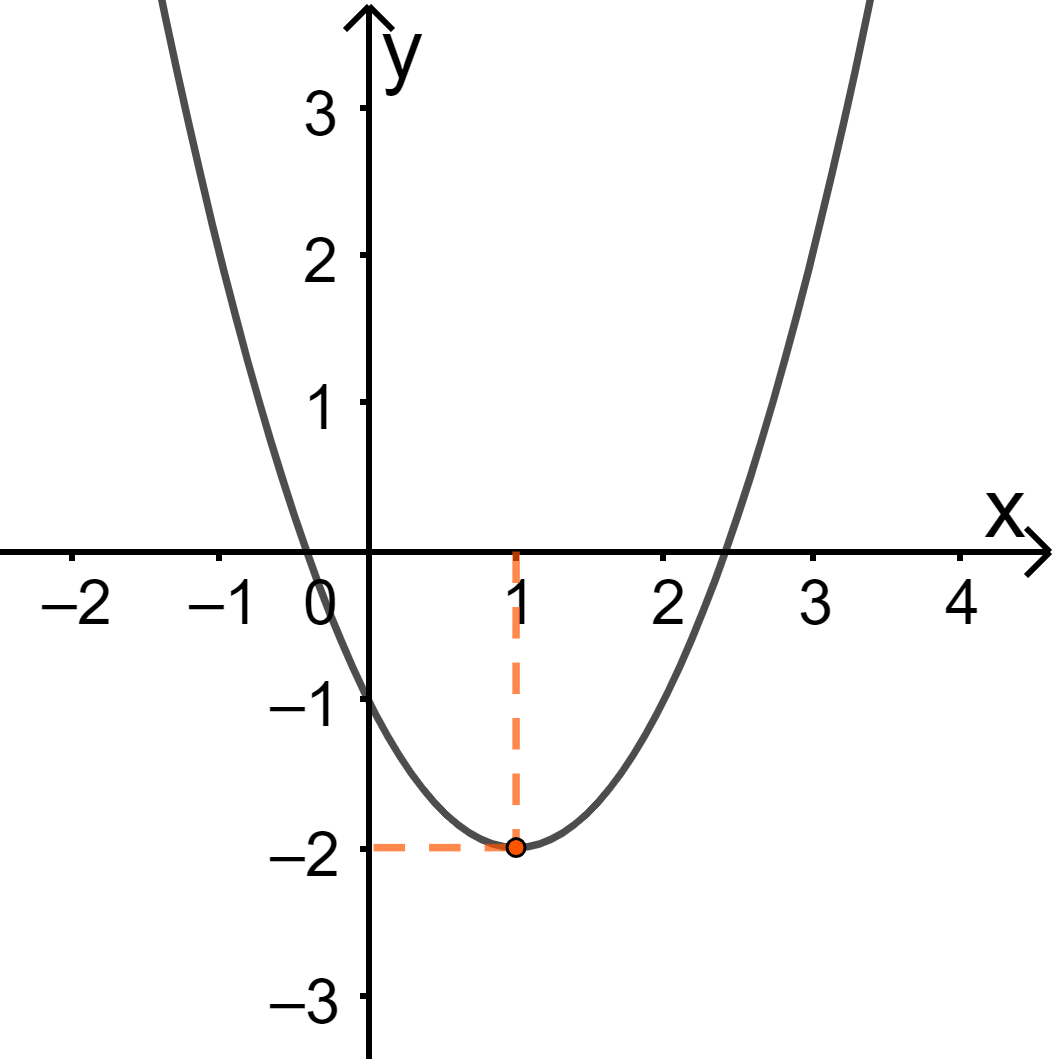
Parabol (P) giao với Oy tại điểm có tọa độ , do đó
(P) có hoành độ đỉnh
Điểm thuộc (P) nên hay
Từ đó ta có hệ phương trình
Vậy parabol cần tìm là
* Vẽ parabol
Đỉnh
Trục đối xứng
Giao với Oy tại A(0;-1), lấy điểm B(2;-1) đối xứng với A qua trục đối xứng
Lấy điểm C(-1;2) và D(3;2) thuộc đồ thị.
