Tailieumoi.vn xin giới thiệu tài liệu Trắc nghiệm Toán lớp 6 Bài 2: Tính chất cơ bản của phân số sách Chân trời sáng tạo. Tài liệu gồm 24 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:

Trắc nghiệm Toán lớp 6 Bài 2: Tính chất cơ bản của phân số

Phần 1. Trắc nghiệm Tính chất cơ bản của phân số

Dạng 1. Tính chất cơ bản của phân số

Câu 1. Quy đồng mẫu số hai phân số $\frac{2}{7};\frac{5}{-8}$ được hai phân số lần lượt là:

A.$\frac{16}{56};\frac{-35}{56}$

B.$\frac{16}{56};\frac{35}{56}$

C.$\frac{16}{56};\frac{35}{-56}$

D.$\frac{-16}{56};\frac{-35}{56}$

Trả lời:

Ta quy đồng $\frac{2}{7}$ và $\frac{-5}{8}(MSC:56)$

$\frac{2}{7}=\frac{2.8}{7.8}=\frac{16}{56};\frac{-5}{8}=\frac{-5.7}{8.7}=\frac{-35}{56}$

Đáp án cần chọn là: A

Câu 2. Mẫu số chung của các phân số $\frac{2}{5};\frac{23}{18};\frac{5}{75}$ là:

A. 180

B. 500

C. 750

D. 450

Trả lời:

Ta có:

5 = 5.1

18 = 2.3²

75 = 3.5²

⇒ BCNN(5; 18; 75) = 2.3².5² = 450

Vậy ta có thể chọn một mẫu chung là 450

Đáp án cần chọn là: D

Câu 3. Mẫu chung nguyên dương nhỏ nhất của các phân số$\frac{19}{3^2\mathrm{.7.11}};\frac{23}{3^3{.7}^2.19}$

A. 3³.7²

B. 3³.7³.11.19

C. 3².7².11.19

D. 3³.7².11.19

Trả lời:

BCNN hay mẫu chung nguyên dương nhỏ nhất của hai mẫu đã cho là

3³.7².11.19

Đáp án cần chọn là: D

Câu 4. Rút gọn phân số $\frac{\left(-2\right).3+6.5}{9.6}$ về dạng phân số tối giản ta được phân số có tử số là

A.$\frac{4}{9}$

B. 31

C. – 1

D. 4

Trả lời:

Ta có:

$\frac{\left(-2\right).3+6.5}{9.6}=\frac{-6+30}{54}=\frac{24}{54}=\frac{24:6}{54:6}=\frac{4}{9}$

Vậy tử số cuả phân số cần tìm là: 4

Đáp án cần chọn là: D

Câu 5. Phân số bằng phân số $\frac{301}{403}$ mà có tử số và mẫu số đều là số dương, có ba chữ số là phân số nào?

A.$\frac{151}{201}$

B.$\frac{602}{806}$

C.$\frac{301}{403}$

D.$\frac{903}{1209}$

Trả lời:

+$\frac{301}{403}=\frac{301.2}{403.2}=\frac{602}{806}\left(TM\right)$

+$\frac{301}{403}=\frac{301.3}{403.3}=\frac{903}{1209}\left(L\right)$

Do đó ở các trường hợp nhân cả tử và mẫu với một số tự nhiên lớn hơn 3 ta cũng đều loại được.

Ngoài ra phân số $\frac{301}{403}$tối giản nên không thể rút gọn được.

Vậy phân số cần tìm là $\frac{602}{806}$

Đáp án cần chọn là: B

Câu 6. Chọn câu sai. Với a; b; m Z; b;m ≠ 0 thì

A.$\frac{a}{b}=\frac{a.m}{b.m}$

B.$\frac{a}{b}=\frac{a+m}{b+m}$

C.$\frac{a}{b}=\frac{-a}{-b}$

D.$\frac{a}{b}=\frac{a:n}{b:n}$với n là ước chung của a; b.

Trả lời:

Dựa vào các tính chất cơ bản của phân số:

$\frac{a}{b}=\frac{a.m}{b.m}$ với m∈Z và m ≠ 0; $\frac{a}{b}=\frac{a:n}{b:n}$ với n ƯC(a;b) và ab = −a − b thì các đáp án A, C, D đều đúng.

Đáp án B sai.

Đáp án cần chọn là: B

Câu 7. Tìm số a; b biết $\frac{24}{56}=\frac{a}{7}=\frac{-111}{b}$

A. a = 3, b = −259

B. a = −3, b = −259

C. a = 3, b = 259

D. a = −3, b = 259

Trả lời:

Ta có:

$$\begin{gathered} \frac{24}{56}=\frac{24:8}{56:8}=\frac{3}{7}\Rightarrow a=3 \\ \frac{3}{7}=\frac{3.\left(-37\right)}{7.\left(-37\right)}=\frac{-111}{-259}=\frac{-111}{b}\Rightarrow b=-259 \end{gathered}$$

Vậy a = 3; b = - 259

Đáp án cần chọn là: A

Câu 8. Tìm x biết $\frac{2323}{3232}=\frac{x}{32}$

A. 101

B. 32

C. – 23

D. 23

Trả lời:

Ta có: $\frac{2323}{3232}=\frac{2323:101}{3232:101}=\frac{23}{32}=\frac{x}{32}\Rightarrow x=23$

Đáp án cần chọn là: D

Câu 9. Tìm x biết $\frac{-5}{-14}=\frac{20}{6-5x}$

A. x = 10

B. x = −10

C. x = 5

D. x = 6

Trả lời:

$\frac{-5}{-14}=\frac{\left(-5\right).\left(-4\right)}{\left(-14\right).\left(-4\right)}=\frac{20}{56}=\frac{20}{6-5x}$

⇒ 56 = 6 − 5x

56 – 6 = −5x

50 = −5x

x = 50:(−5)

x = −10

Đáp án cần chọn là: B

Câu 10. Phân số $\frac{-m}{-n};n,m\in Z;n\ne 0$ bằng phân số nào sau đây

A.$\frac{m}{n}$

B.$\frac{n}{m}$

C.$\frac{-n}{m}$

D.$\frac{m}{-n}$

Trả lời:

Ta có:$\frac{-m}{-n}=\frac{m}{n}$

Đáp án cần chọn là: A

Dạng 2. Các dạng toán về tính chất cơ bản của phân số

Câu 1. Rút gọn biểu thức $A=\frac{3.\left(-4\right).60-60}{50.20}$

A.$\frac{-13}{25}$

B.$\frac{-18}{25}$

C.$\frac{-6}{25}$

D.$\frac{-39}{50}$

Trả lời:

Ta có:

$$\begin{gathered} A=\frac{3.\left(-4\right).60-60}{50.20}=\frac{\left[3.\left(-4\right)-1\right].60}{50.20} \\ =\frac{-13.60}{50.20}=\frac{-13.3}{50}=\frac{-39}{50} \end{gathered}$$

Đáp án cần chọn là: D

Câu 2. Phân số nào sau đây là kết quả của biểu thức $\frac{\mathrm{2.9.52}}{22.\left(-72\right)}$ sau khi rút gọn đến tối giản?

A.$\frac{-13}{22}$

B.$\frac{13}{22}$

C.$\frac{-13}{18}$

D.$\frac{-117}{198}$

Trả lời:

$\frac{\mathrm{2.9.52}}{22.\left(-72\right)}=\frac{{2.3}^2{.2}^2.13}{\mathrm{2.11.}\left(-2^3{.3}^2\right)}=\frac{2^3{.3}^2.13}{-2^4{.3}^2.11}=\frac{13}{-2.11}=\frac{-13}{22}$

Đáp án cần chọn là: A

Câu 3. Biểu thức $\frac{5^{12}{.3}^9-5^{10}{.3}^{11}}{5^{10}{.3}^{10}}$ sau khi đã rút gọn đến tối giản có mẫu số dương là:

A. 16

B. 3

C.$\frac{16}{5}$

D.$\frac{16}{3}$

Trả lời:

$\frac{5^{12}{.3}^9-5^{10}{.3}^{11}}{5^{10}{.3}^{10}}=\frac{5^{10}{.3}^9.\left(5^2-3^2\right)}{5^{10}{.3}^{10}}=\frac{5^{10}{.3}^9.16}{5^{10}{.3}^{10}}=\frac{16}{3}$

Vậy mẫu số của phân số đó là 3

Đáp án cần chọn là: B

Câu 4. Sau khi rút gọn biểu thức $\frac{5^{11}{.7}^{12}+5^{11}{.7}^{11}}{5^{12}{.7}^{12}+{9.5}^{11}{.7}^{11}}$ ta được phân số $\frac{a}{b}$. Tính tổng a + b.

A. 26

B. 13

C. 52

D. 8

Trả lời:

$\frac{5^{11}{.7}^{12}+5^{11}{.7}^{11}}{5^{12}{.7}^{12}+{9.5}^{11}{.7}^{11}}=\frac{5^{11}{.7}^{11}\left(7+1\right)}{5^{11}{.7}^{11}\left(5.7+9\right)}=\frac{8}{44}=\frac{2}{11}$

Do đó a = 2, b = 11 nên a + b = 13

Đáp án cần chọn là: B

Câu 5. Tìm phân số bằng với phân số $\frac{200}{520}$ mà có tổng của tử và mẫu bằng 306

A.$\frac{84}{222}$

B.$\frac{200}{520}$

C.$\frac{85}{221}$

D.$\frac{100}{260}$

Trả lời:

Ta có: $\frac{200}{520}=\frac{5}{13}$ nên có dạng tổng quát là $\frac{5k}{13k}$(k∈Z, k ≠ 0)

Do tổng và tử và mẫu của phân số cần tìm bằng 306 nên:

5k + 13k = 306

18k = 306

k = 306:18

k = 17

Vậy phân số cần tìm là $\frac{5.17}{13.17}=\frac{85}{221}$

Đáp án cần chọn là: C

Câu 6. Phân số nào dưới đây là phân số tối giant?

A.$\frac{-2}{4}$

B.$\frac{-15}{-96}$

C.$\frac{13}{27}$

D.$\frac{-29}{58}$

Trả lời:

Đáp án A: ƯCLN(2;4)=2≠1 nên loại.

Đáp án B: ƯCLN(15;96)=3≠1 nên loại.

Đáp án C: ƯCLN(13;27)=1 nên C đúng.

Đáp án D: ƯCLN(29;58)=29≠1 nên D sai.

Đáp án cần chọn là: C

Câu 7. Nhân cả tử số và mẫu số của phân số $\frac{14}{23}$ với số nào để được phân số $\frac{168}{276}$ ?

A. 14

B. 23

C. 12

D. 22

Trả lời:

Ta có: 168:14 = 12 và 276:23 = 12 nên số cần tìm là 12.

Đáp án cần chọn là: C

Câu 8. Rút gọn phân số $\frac{600}{800}$ về dạng phân số tối giản ta được:

A.$\frac{1}{2}$

B.$\frac{6}{8}$

C.$\frac{3}{4}$

D.$\frac{-3}{4}$

Trả lời:

Ta có: ƯCLN(600,800) = 200 nên: $\frac{600}{800}=\frac{600:200}{800:200}=\frac{3}{4}$

Đáp án cần chọn là: C

Câu 9. Hãy chọn phân số không bằng phân số $\frac{-8}{9}$ trong các phân số dưới đây?

A.$\frac{16}{-18}$

B.$\frac{-72}{81}$

C.$\frac{-24}{-27}$

D.$\frac{-88}{99}$

Trả lời:

Đáp án A: $\frac{16}{-18}=\frac{-16}{18}=\frac{-16:2}{18:2}=\frac{-8}{9}$ nên A đúng

Đáp án B: $\frac{-72}{81}=\frac{-72:9}{81:9}=\frac{-8}{9}$ nên B đúng

Đáp án C:$\frac{-24}{-27}=\frac{24}{27}=\frac{24:3}{27:3}=\frac{8}{9}\ne \frac{-8}{9}$nên C sai

Đáp án D: $\frac{-88}{99}=\frac{-88:11}{99:11}=\frac{-8}{9}$ nên D đúng

Đáp án cần chọn là: C

Câu 10. Rút gọn phân số$\frac{4.8}{64.\left(-7\right)}$ ta được phân số tối giản là:

A.$\frac{-1}{7}$

B.$\frac{-1}{14}$

C.$\frac{4}{-56}$

D.$\frac{-1}{70}$

Trả lời:

Ta có:$\frac{4.8}{64.\left(-7\right)}=\frac{4.8}{\mathrm{2.4.8.}\left(-7\right)}=\frac{1}{2.\left(-7\right)}=\frac{-1}{14}$

Đáp án cần chọn là: B

Câu 11. Viết dạng tổng quát của các phân số bằng với phân số $\frac{-12}{40}$

A.$\frac{-3k}{10k},k\in Z$

B.$\frac{-3k}{10},k\in Z,k\ne 0$

C.$\frac{-3k}{10k},k\in Z,k\ne 0$

D.$\frac{-3}{10}$

Trả lời:

- Rút gọn phân số: $\frac{-12}{40}=\frac{-12:4}{40:4}=\frac{-3}{10}$

- Dạng tổng quát của phân số đã cho là:$\frac{-3k}{10k},k\in Z,k\ne 0$

Đáp án cần chọn là: C

Câu 12. Tìm phân số tối giản $\frac{a}{b}$ biết rằng lấy tử cộng với 6, lấy mẫu cộng với 14 thì ta được phân số bằng $\frac{3}{7}$ .

A.$\frac{4}{5}$

B.$\frac{7}{3}$

C.$\frac{3}{7}$

D.$\frac{-3}{7}$

Trả lời:

$\frac{a+6}{b+14}=\frac{3}{7}$

7.(a + 6) = 3.(b + 14)

7a + 42 = 3b + 42

7a = 3

Đáp án cần chọn là: C

Câu 13. Cho các phân số $\frac{6}{n+8};\frac{7}{n+9};\frac{8}{n+10};\mathrm{...};\frac{35}{n+37}$ . Tìm số tự nhiên n nhỏ nhất để các phân số trên tối giản.

A. 35

B. 34

C. 37

D. 36

Trả lời:

Các phân số đã cho đều có dạng$\frac{a}{a+\left(n+2\right)}$

Và tối giản nếu a và n + 2 nguyên tố cùng nhau

Vì: [a + (n + 2)] – a = n + 2

với a = 6; 7; 8;.....; 34; 35

Do đó n + 2 nguyên tố cùng nhau với các số 6; 7; 8;.....; 34; 35

Số tự nhiên n + 2 nhỏ nhất thỏa mãn tính chất này là 37

Ta có n + 2 = 37 nên n = 37 – 2 = 35

Vậy số tự nhiên nhỏ nhất cần tìm là 35

Đáp án cần chọn là: A

Câu 14. Rút gọn phân số $\frac{-12a}{24},a\in Z$ ta được:

A.$\frac{a}{2}$

B.$\frac{1}{2}$

C.$\frac{-1}{2}$

D.$\frac{-a}{2}$

Trả lời:

Ta có:$\frac{-12a}{24}=\frac{\left(-1\right)\mathrm{.12.}a}{12.2}=\frac{\left(-1\right).a}{2}=\frac{-a}{2}$

Đáp án cần chọn là: D

Phần 2. Lý thuyết  Tính chất cơ bản của phân số

1. Tính chất 1

Tính chất 1: Nếu nhân cả tử số và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.

Ví dụ 1. Cho phân số 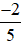. Nhân cả tử và mẫu của phân số  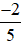với 3, ta được:

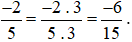
Khi đó, ta có phân số mới là 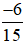 bằng phân số đã cho là .

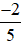Nhận xét: Có thể biểu diễn số nguyên ở dạng phân số với mẫu số (khác 0) tùy ý.

- Áp dụng tính chất 1, ta có thể quy đồng mẫu số hai phân số bằng cách nhân tử và mẫu mỗi phân số với số nguyên thích hợp.

Ví dụ 2. Có thể biểu diễn số −8 ở dạng phân số có mẫu số là 3 như sau:

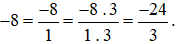
Ví dụ 3. Quy đồng mẫu số hai phân số .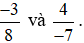

Lời giải: 

Quy đồng mẫu số hai phân số ta thực hiện như sau:

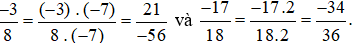
Nhận xét: Mẫu số giống nhau ở hai phân số là −56 còn gọi là mẫu số chung của hai phân số.

Khi quy đồng mẫu số hai phân số, có thể có nhiều cách chọn mẫu số chung.

Chú ý: Có thể quy đồng mẫu số của nhiều phân số bằng cách tìm mẫu số chung của nhiều phân số.

Ví dụ 4. Quy đồng mẫu số của ba phân số .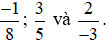

Lời giải: 

Quy đồng mẫu số ba phân số, ta nhân cả tử và mẫu của mỗi phân số nhân với tích hai mẫu số của hai phân số còn lại.

Ta thực hiện như sau:

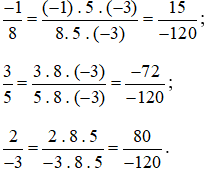
Mẫu số chung của ba phân số trên là −120.

2. Tính chất 2

Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.

Ví dụ 5. Cho phân số 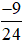. Chia cả tử và mẫu của phân số  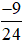cho 3, ta được:

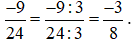
Khi đó, ta có phân số mới là 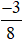 bằng phân số đã cho là .

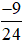Áp dụng tính chất 2, ta có thể rút gọn phân số bằng cách chia cả tử và mẫu cho cùng ước chung khác 1 và −1.

Ví dụ 6. Rút gọn phân số .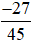

Lời giải: 

Chia cả tử và mẫu của phân số 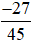 cho 9, ta được:

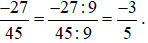
Nhận xét: Sau khi rút gọn ta được phân số mới là 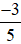 bằng phân số đã cho là .

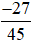Chú ý: Khi rút gọn phân số, có thể được nhiều kết quả, nhưng các phân số ở các kết quả đó đều bằng nhau.

Ví dụ 7. Rút gọn phân số .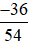

Lời giải: 

Chia cả tử và mẫu của phân số 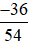 cho 2, ta được:

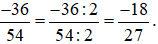
Chia cả tử và mẫu của phân số 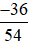 cho 3, ta được:

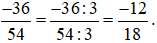
Chia cả tử và mẫu của phân số 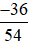 cho 6, ta được:

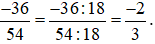
Nhận xét: Khi rút gọn phân số 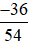, ta thu được nhiều kết quả như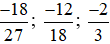  

Các phân số 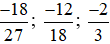 đều bằng nhau.

Tổng quát: .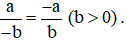

Chú ý: Mỗi phân số đều có nhiều phân số bằng nó.

Ví dụ 8. Viết phân số 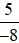 thành phân số có mẫu dương.

Lời giải: 

Phân số 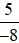 có mẫu là số nguyên âm. 

Do đó để viết phân số 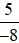 thành phân số có mẫu dương thì ta chia cả tử và mẫu của phân số này cho cùng một số nguyên âm và là ước chung của 5 và (−8) là (−1).

Khi đó ta có:

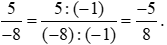
Vậy phân số 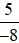 được viết thành phân số có mẫu dương là .

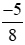Xem thêm các bài trắc nghiệm Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 1: Phân số với tử số và mẫu số là số nguyên

Trắc nghiệm Bài 2: Tính chất cơ bản của phân số

Trắc nghiệm Bài 3: So sánh phân số

Trắc nghiệm Bài 4: Phép cộng và phép trừ phân số

Trắc nghiệm Bài 5: Phép nhân và phép chia phân số