Tailieumoi.vn xin giới thiệu chuyên đề Phép đối xứng tâm thuộc chương trình Toán 11. Chuyên đề gồm 5 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.

Chuyên đề Phép đối xứng tâm

Phần 1: Tìm ảnh của một điểm qua phép đối xứng tâm cực hay

A. Phương pháp giải

Biểu thức toạ độ của phép đối xứng tâm

Trong hệ tọa độ Oxy:

• Nếu tâm đối xứng là O(0;0), với mỗi M(x;y) gọi M' = D_O(M) = (x';y') thì 

• Nếu tâm đối xứng I(a;b) bất kì, với mỗi M(x;y) gọi M' = D_I(M) = (x';y') thì 

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy. Tìm ảnh của điểm M(-2020;2019) qua phép đối xứng tâm O(0;0)

Hướng dẫn giải:

Biểu thức tọa độ của phép đối xứng tâm O(0;0) là 

Ví dụ 2: Trong mặt phẳng tọa độ Oxy. Tìm ảnh của điểm M(2;–1) qua phép đối xứng tâm I(1;2) là:

Hướng dẫn giải:

Ví dụ 3: Trong mặt phẳng Oxy, biết M'(5;3) là ảnh của M qua phép đối xứng tâm I(4;1). Tìm tọa độ điểm M.

Hướng dẫn giải:

+ Giải sử M(x,y). Thay biểu thức tọa độ của phép đối xứng tâm I(4;1) ta được: 

Ví dụ 4: Trong mặt phẳng Oxy, Cho M(3;7) và M'(5;3). Biết M’ là ảnh của M qua phép đối xứng tâm I. Tìm tọa độ điểm I.

Hướng dẫn giải:

Phần 2: Tìm ảnh của một đường thẳng qua phép đối xứng tâm cực hay

A. Phương pháp giải

[Cách 1]. Sử dụng tính chất:

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

[Cách 2]. Sử dụng biểu thức tọa độ (phương pháp quỹ tích)

Trong hệ tọa độ Oxy

● Nếu tâm đối xứng là O(0;0), với mỗi M(x;y) gọi M' = D_O(M) = (x';y') thì 

● Nếu tâm đối xứng I(a;b) bất kì, với mỗi M(x;y) gọi M' = D_I(M) = (x';y') thì 

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng Oxy cho đường thẳng d có phương trình: x + y + 2 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng tâm I(1;0)

Hướng dẫn giải:

d:x + y + 2 = 0 lấy 2 điểm A(0,-2), B(-2,0) thuộc d.

Gọi A’, B’ là ảnh của A,B qua phép đối xứng tâm I. Khi đó ta có:

Gọi d’ là ảnh của d qua phép đối xứng tâm I. Khi đó d’ đi qua 2 điểm A’B’ nên có phương trình d': x⁡ + y⁡- 4 = 0

Vậy ảnh của d là d': x⁡ + y⁡- 4 = 0

Ví dụ 2: Trong mặt phẳng Oxy cho đường thẳng d có phương trình: 2x + y + 1 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng tâm I(1;0)

Hướng dẫn giải:

• d: 2x + y + 1 = 0 lấy 2 điểm A(0,-1), B (-1,1) thuộc d. Gọi A’, B’ là ảnh của A, B qua phép đối xứng tâm I. Khi đó ta có:

• Gọi d’ là ảnh của d qua phép đối đối xứng tâm I. Khi đó, d’ đi qua 2 điểm A’ và B’ nên có phương trình d’: đi qua A’( 2;1), 

Phương trình d’: 2(x - 2) + 1(y - 1) = 0 hay 2x + y - 5 = 0

Vậy ảnh của d là d': 2x ⁡ + y - 5 = 0

Ví dụ 3: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0, điểm I(2;-4). Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng tâm I

Hướng dẫn giải:

Lấy M(x;y) thuộc d, phép đối xứng tâm I(x₀,y₀) biến M(x;y) thành M'(x',y') thì 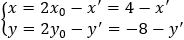. Thay vào phương trình d ta được

2(4 - x') - 6(-8 - y') + 5 = 0 ⇔ 2x' - 6y' - 61 = 0 hay 2x - 6y - 61 = 0.

Phần 3: Tìm ảnh của một đường tròn qua phép đối xứng tâm cực hay

A. Phương pháp giải

[1]. PP1: Sử dụng tính chất: Phép đối xứng tâm biến đường tròn thành đường tròn có cùng bán kính.

Bước 1. Xác định tâm I , bán kính R của (C)

Bước 2. Tìm ảnh I’ của tâm I qua phép đối xứng tâm

Bước 3. Viết phương trình đường tròn có tâm I’ và bán kính R’=R

[2]. PP2: Sử dụng biểu thức tọa độ (Phương pháp quỹ tích)

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, tìm phương trình đường tròn (C') là ảnh của đường tròn (C): (x - 5)² + (y + 3)² = 16 qua phép đối xứng tâm O(0;0).

Hướng dẫn giải:

Gọi I' là điểm đối xứng của I(5;-3) qua tâm O(0;0), suy ra I'(-5;3).

Phép đối xứng tâm bảo toàn khoảng cách nên R' = R = 4

Vậy đường tròn (C') có tâm I'(-5;3), bán kính R' = 3 nên (C'): (x + 5)² + (y - 3)² = 16

Cách 2. Biểu thức tọa độ của phép đối xứng tâm O(0;0) là 

Thay vào (C) ta được (-x' - 5)² + (-y' + 3)² = 16 ⇔ (x' + 5)² + (y' - 3)² = 16.

Ví dụ 2: Trong mặt phẳng Oxy cho đường tròn (O;R): x² + y² + 2x - 6y + 6 = 0 điểm I(1;2). Tìm ảnh của (O;R) qua phép đối xứng tâm I

Hướng dẫn giải:

Gọi M(x;y) là điểm bất kỳ thuộc (O;R) và (E). Từ công thức chuyển trục ta có:

 (2 - x')² + (4 - y')² + 2(2 - x') - 6(4 - y') + 6 = 0

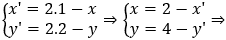
⇔ x'² + y'² - 6x' - 2y' + 6 = 0

⇔ x² + y² - 6x - 2y + 6 = 0

Cách 2. x² + y² + 2x - 6y + 6 = 0 có tâm J(-1;3), R = 2

Ta chỉ tìm J’(x;y) là ảnh của J qua phép đối xứng tâm I(1;2) bằng công thức chuyển trục tọa độ: 

Do đó (O’): (x - 3)² + (y - 1)² = 4 là ảnh của (O;R) qua phép đối xứng tâm I.

Ví dụ 3: Trong mặt phẳng Oxy, tìm ảnh của đường trònx² + (y – 2)² = 4. qua phép đối xứng tâm I(-2;-1):

Hướng dẫn giải:

Đường tròn có tâm O(0,2), bán kính r = 2

Gọi O' là ảnh của O qua phép đối xứng tâm I khi đó ta có

x_O' = 2x_I - x_O = -4; y_O' ⁡ = 2y_I - y_O = -4 ⇒ O'(-4;-4)

Như vậy ảnh của đường tròn qua phép đối xứng tâm là: (x + 4)² + (y + 4)² = 4

Phần 4: Cách tìm tâm đối xứng của một hình cực hay

A. Phương pháp giải

Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó.

Khi đó ta nói H là hình có tâm đối xứng.

B. Ví dụ minh họa

Ví dụ 1: Tìm tâm đối xứng biến điểm A(1;3) thành điểm A'(1;7).

Hướng dẫn giải:

Từ giả thiết, suy ra I(a;b) là trung điểm của 

Vậy tâm đối xứng cần tìm là: I(1;5)

Ví dụ 2: Trong mặt phẳng Oxy cho đường thẳng d: x - 2y + 2 = 0 và d’: x - 2y - 8 = 0. Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó.

Hướng dẫn giải:

Để thỏa mãn yêu cầu bài toán thì ta làm như sau:

- Gọi M(x;y) thuộc d, M’(x’;y’) thuộc d’. Giả sử tâm đối xứng là I(a;b), thì theo công thức chuyển trục:

- Để trục Ox thành chính nó thì tâm đối xứng phải có dạng: I(a;0) tức là b = 0

- Từ hai kết quả trên ta có:

Ví dụ 3: Tìm tâm đối xứng của các hình sau

a) Hình tròn

b) Hình bình hành.

Hướng dẫn giải:

a)Tâm đối xứng của hình tròn là tâm của hình tròn đó.

b)Tâm đối xứng của hình hình bình hành là giao điểm của hai đường chéo.