Tài liệu Bộ đề thi Toán lớp 7 học kì 1 năm học 2024 - 2025 gồm 13 đề thi tổng hợp từ đề thi môn Toán 7 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 1 Toán lớp 7. Mời các bạn cùng đón xem:
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
Bài 1 (2,5 điểm)Thực hiện phép tính:
a) \[\frac{8}{{15}}.\frac{7}{{13}} + \frac{8}{{15}}.\frac{6}{{13}}\]
b) \[\frac{5}{2} - {\left( { - \frac{{2018}}{{2019}}} \right)^0} + {\left( { - 3} \right)^2}:\frac{2}{7}\]
c) \[3.\,\sqrt {\frac{1}{9}} + \sqrt {36} - 2.\,\sqrt {25} \]
Bài 2 (1,5 điểm) Tìm x biết:
a) \(\frac{2}{3} - \left( {\frac{3}{4} + x} \right) = \frac{1}{3}\)
b) \(\left| {x - \frac{5}{2}} \right| - \frac{1}{2} = \frac{9}{2}\)
Bài 3 (1 điểm) Tìm hai số a, b biết rằng: 2a = 5b và 3a + 4b = 46
Bài 4 (1,5 điểm). Một cửa hàng có 3 tấm vải dài tổng cộng 93m. Sau khi bán đi 1/2 tấm vải thứ nhất, 2/3 tấm vải thứ hai, 4/5 tấm vài thứ ba thì số mét vải còn lại ở ba tấm vải bằng nhau. Tính chiều dài mỗi tấm vải lúc đầu.
Bài 5 (3,5 điểm) Cho tam giác DEF nhọn, kẻ DK\( \bot \) EF (K \( \in \)EF). Trên tia đối của tia KD lấy điểm A sao cho KA = KD.
a) Chứng minh \(\Delta \)DKE = \(\Delta \)AKE
b) Chứng minh rằng EF là tia phân giác của góc DEA.
c) Chứng minh rằng \(\widehat {EDF} = \widehat {EAF}\)
d) Gọi H là trung điểm của EF, trên tia đối của tia HD ta lấy điểm B sao cho H là trung điểm của DB. Chứng minh rằng BF = AE.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 2)
Bài 1 (1,5 điểm). Thực hiện phép tính:
a) \[\frac{3}{2} - \frac{3}{2}:\frac{{ - 1}}{{{2^3}}}\]
b) \[23\frac{1}{3}:\frac{{ - 1}}{{{2^2}}} - 13\frac{1}{3}:\frac{{ - 1}}{{{2^2}}} + 5\sqrt {\frac{9}{{25}}} \]
Bài 2 (1,5 điểm). Cho hàm số: \[y = 3x\]
a) Vẽ đồ thị hàm số trên.
b) Điểm \[M\left( { - 2;\,\, - 6} \right)\] có thuộc đồ thị hàm số \[y = 3x\]? Vì sao?
Bài 3 (2,5 điểm). Tìm x, y biết:
a) \[\frac{1}{3} + \frac{2}{3}:x = - 2\]
b) \(7x = 3y\) và \(2x - y = 16\)
c) Một nhân viên văn phòng có thể đánh máy được 160 từ trong 2,5 phút. Hỏi cần bao nhiêu phút để người đó đánh được 800 từ ? (giả thiết rằng thời gian để đánh được các từ là như nhau).
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A có \[\widehat B = {60^ \circ }\]. Vẽ \[AH \bot BC\] tại \[H\].
a) Tính số đo \[\widehat {HAB}\].
b) Trên cạnh AC lấy điểm D sao cho AD = AH. Gọi I là trung điểm của cạnh HD.
Chứng minh \[\Delta AHI = \Delta ADI\]. Từ đó suy ra \[AI \bot HD\].
c) Tia AI cắt cạnh HC tại điểm K.
Chứng minh \[\Delta AHK = \Delta ADK\], từ đó suy ra AB // KD.
d) Trên tia đối của tia HA lấy điểm E sao cho HE = AH. Chứng minh H là trung điểm của BK và ba điểm D, K, E thẳng hàng.
Bài 5 (1,0 điểm).
a) Tính: \(\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{19.21}}\)
b) Chứng minh: \(A = \frac{1}{{1.3}} + \frac{1}{{3.5}} + ... + \frac{1}{{\left( {2n - 1} \right)\left( {2n + 1} \right)}} < \frac{1}{2}\)
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 3)
Bài 1 (2 điểm): Thực hiện phép tính:
a) \[\frac{7}{2} \cdot \frac{{11}}{6} - \frac{7}{2} \cdot \frac{5}{6}\]
b) \[3\frac{3}{3} \cdot \frac{1}{3} - \frac{3}{4} \cdot \frac{1}{3}\]
c) \[\left| {\frac{{11}}{3}} \right| - {\left( {\frac{{ - 1}}{2}} \right)^2} - 4\frac{1}{2}\]
d) \({\left( {\frac{3}{2} - \frac{5}{4} + \frac{1}{3}} \right)^2}:\left( {\frac{4}{3} + 2\frac{3}{2} - \frac{3}{4}} \right)\)
Bài 2 (1,5 điểm): Tìm x biết:
a) \(3 - x = {\left( {\frac{{ - 3}}{2}} \right)^2}\)
b) \(\frac{3}{{x - 2}} = \frac{1}{5}\) với \[x \ne - 2\]
c) \(9 - 8\left| {2 - x} \right| = 3\)
Bài 3 (1,5 điểm):
Trong buổi tổng kết cuối năm, ban tổ chức câu lạc bộ em yêu thích bộ môn đã thưởng 210 quyển vở cho câu lạc bộ môn Toán, Văn, Anh theo tỉ lệ 6, 5, 4. Hỏi mỗi câu lạc bộ đã nhận được bao nhiêu quyển vở
Bài 4 (1 điểm): Cho hai tam giác ABC vuông tại A, góc ABC bằng 500. Kẻ AH vuông góc với Bc tại H. Tính góc HAC.
Bài 5 (3,5 điểm):
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = AM.
a) Chứng minh: ∆ ABM = ∆ ECM
b) Chứng minh: AB = CE và AB // CE
c) Chứng minh: AC // BE
d) Trên đoạn thẳng AB lấy điểm I, trên đoạn thẳng CE lấy điểm K sao cho AI = EK. Chứng minh: 3 điểm I, M, K thẳng hàng.
Bài 6 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: \[A = 9 - \left| {2x - \frac{1}{{10}}} \right|\]
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 4)
Bài 1: (2,5 điểm) Thực hiện phép tính:
a) \(\frac{{ - 7}}{{10}} + \frac{6}{{23}} + \frac{{17}}{{10}} + \frac{{17}}{{23}}\)
b) \[\sqrt {144} - \left| {\frac{{ - 5}}{4}} \right|{\rm{:}}{\left( {\frac{1}{3} - \frac{1}{2}} \right)^2}\]
c) \[\frac{{{3^{29}}{\rm{. }}{{\rm{4}}^{16}}}}{{{{27}^9}{\rm{.}}{{\rm{8}}^{11}}}}\]
Bài 2: (1,5 điểm) Tìm x, biết:
a) \[\frac{7}{5} - x = \frac{2}{3}\]
b) \( - \frac{2}{3}x{\rm{ + 1,2 = }}{\left( { - \frac{1}{2}} \right)^2}\)
Bài 3: (1,0 điểm) Trong đợt phát động phong trào “Thu hồi pin cũ, góp phần giữ xanh môi trường” năm học 2019 – 2020. Kết thúc phong trào trường THCS A thu được 250 cục pin cũ của các em học sinh khối 6, khối 7, khối 8, khối 9. Biết rằng số cục pin cũ đã nộp của các khối 6, khối 7, khối 8, khối 9 lần lượt tỉ lệ với 9; 7; 5; 4. Hỏi mỗi khối đã nộp bao nhiêu cục pin cũ?
Bài 4: (1,0 điểm) Cho hàm số y = f(x) = 3x – 2. Tính f(1), f(–2).
Bài 5: (1,0 điểm) Mẹ bạn Mai dự định tổ chức sinh nhật lần thứ 13 cho bạn Mai (số người tham dự buổi tiệc gồm Mai và các bạn của Mai) tại Nhà hàng gà rán KFC. Giá một phần ăn của mỗi người tham dự là 79 000 đồng.
a) Gọi số tiền mẹ bạn Mai phải trả cho buổi tiệc sinh nhật là y (đồng), số người tham dự buổi tiệc là x (người). Em hãy viết công thức để thể hiện số tiền phải trả theo số người tham dự buổi tiệc.
b) Mẹ bạn Mai đã thanh toán số tiền cho buổi tiệc là 790 000 đồng. Hỏi có bao nhiêu bạn của Mai đã tham dự buổi tiệc?
Bài 6: (0,5 điểm) Có một con ốc sên leo lên một cột điện cao 15m. Cứ 12 tiếng đầu nó bò lên 3m; 12 tiếng sau nó lại bò xuống 2m. Hỏi bao lâu nó bò tới đỉnh cột?
Bài 7: (2,5 điểm) Cho DABC có AB = AC. Gọi M là trung điểm BC.
a) Chứng minh DABM = DACM.
b) Trên cạnh AM lấy điểm K bất kỳ. Chứng minh KB = KC.
c) Tia BK cắt cạnh AC tại F, tia CK cắt cạnh AB tại E. Chứng minh EF // CB
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 5)
Bài 1 (2,25 điểm) Thực hiện phép tính:
a) \[\frac{2}{5}\,\, + \,\,\frac{{15}}{4}\,\,.\,\,\left( { - 2\,\, + \,\,\frac{6}{5}} \right)\,\,\]
b) \[\frac{3}{4}\,\, + \,\,\left[ {{{\left( { - \frac{1}{2}} \right)}^3}\,:\,\,\frac{5}{4}\,\, - \,\,0,25\,.\,\sqrt {\frac{9}{{25}}\,\,} } \right]\,\]
Bài 2 (2,25 điểm) Tìm x, biết:
a) \[\frac{{ - 3}}{4}x\,\, + \,\,\frac{7}{{11}}\,\, = \,\,\frac{3}{{22}}\]
b) \[\,\left| {\,1\frac{1}{3}\,\, - \,\,0,4x\,} \right|\,\, - \,\,\frac{5}{{12}}\,\, = \,\,\frac{1}{4}\]
Bài 3 (2,0 điểm):
a) Khối 7 của trường THCS A có 4 lớp. Trong hội thi Văn hay Chữ tốt, cả khối có 156 bạn tham gia. Biết rằng số bạn tham gia dự thi của các lớp 7A, 7B, 7C, 7D lần lượt tỉ lệ với 8; 10; 9; 12. Em hãy tính số bạn tham gia thi Văn hay Chữ tốt của mỗi lớp nói trên.
b) Lớp 7A nhận chăm sóc mảnh vườn kề bên lớp. Sau khi đo đạc, bạn An nói: “Tỉ số của chiều rộng và chiều dài của mảnh vườn này là 0,6”. Bạn Bình nói: “Mảnh vườn này có chiều rộng ngắn hơn chiều dài 4m”. Biết rằng hai bạn đều nói đúng. Em hãy tính diện tích của mảnh vườn nói trên.
Bài 4 (3,5 điểm):
Cho tam giác ABC, M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh DABM = DDCM.
b) Trên tia DC lấy điểm E sao cho C là trung điểm của đoạn thẳng DE.
Chứng minh: DABC = DCEA.
c) Gọi I là trung điểm của đoạn thẳng AC. Chứng minh ba điểm B, I, E thẳng hàng.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 6)
Câu 1 (2 điểm): Tính giá trị của các biểu thức
a) \[5\frac{5}{{27}} + \frac{7}{{23}} + 0,5 + \frac{{ - 5}}{{27}} + \frac{{16}}{{23}}\]
b) \(\frac{{19}}{{11}}.\frac{6}{5} + \frac{{{6^2}}}{{11}}.\frac{6}{5} - \sqrt {25} \)\(\)
c) \(2.\sqrt {\frac{{25}}{{64}}} + {\left( { - 2018} \right)^0} - \left| {\frac{{ - 1}}{4}} \right|\)
Câu 2 (2,5 điểm): Tìm \[x\], biết:
a) \({\left( {\frac{3}{2}} \right)^2} - 2x = \frac{1}{4}\)
b) \(\frac{2}{7}x + \frac{1}{2} = \frac{{ - 3}}{4}:\sqrt {\frac{{49}}{{64}}} \)
c) \(\frac{{{2^{x + 1}}}}{{ - 8}} = \frac{{ - 2}}{4}\)
d) \(\,\,\left| {x + \frac{3}{4}} \right| - \frac{1}{2} = 0\)
Câu 3 (1,5 điểm): Trong một hội thi thiết kế tập san, vẽ tranh tuyên truyền phòng chống HIV/AIDS, ban tổ chức nhận được 250 bức tranh của bốn khối 6; 7; 8; 9. Biết rằng số bức tranh của các khối 6, 7, 8, 9 lần lượt tỉ lệ với 2; 5; 8; 10. Hỏi khối 7; 8 đã gửi về ban tổ chức bao nhiêu bức tranh?
Câu 4 (0,5 điểm): Một máy photocopy siêu tốc in được 1 bản trong \(\frac{1}{3}\) giây. Hỏi với tốc độ như vậy, để in được 3060 đề kiểm tra thì máy phải in trong thời gian bao nhiêu phút?
Câu 5 (0,5 điểm): Bạn Hòa đặt xe Grab đi từ nhà đến trường với vận tốc 50km/h hết 15 phút. Hỏi lúc về Hòa đi xe đạp điện với bạn Bình cũng theo con đường ấy với vận tốc 25km/h thì hết bao nhiêu phút?
Câu 6 (3 điểm): Cho ΔABC có ba góc nhọn (AB < AC). Gọi M là trung điểm của BC. Vẽ tia AM, trên tia AM lấy điểm D sao cho MA = MD.
a) Chứng minh ΔAMB = ΔDMC
b) Vẽ AH ^ BC tại H; DK ^ BC tại K. Chứng minh AH = DK
c) Gọi E là trung điểm của AH, F là trung điểm của DK. Chứng minh E, M, F thẳng hàng.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 7)
Câu 1. (2,0 điểm) Thực hiện các phép tính:
\[a)\,\,\frac{2}{3} - \frac{5}{3}:\frac{3}{4} + 25\% \]
\[b)\,\,{\left( { - \,\frac{1}{4}} \right)^2}\,.\,\,8\,\,\, + \,\,\sqrt {1\frac{9}{{16}}} \,\,:\,\,2\frac{1}{2}\,\, - \,\,\,\left| {\frac{{ - 3}}{4}} \right|\,\]
Câu 2. (1,5 điểm) Tìm x, biết:
\(a)\,\, - 1,5 + \frac{{15}}{2}x = \frac{3}{4}\)
\[b)\,\,\,\left| {x - \frac{1}{3}} \right| + \frac{1}{2} = \frac{5}{8}\]
Câu 3. (1,0 điểm) Cho biết hai đại lượng \[x\] và \[y\] tỉ lệ thuận với nhau và khi x = 20 thì y = 12.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.
b) Tính giá trị của \[x\] khi \[{\mathop{\rm y}\nolimits} = \frac{{ - 1}}{3}\].
Câu 4. (0,5 điểm) “…Theo thống kê sơ bộ của các bệnh viện, trong tổng số bệnh nhân mắc bệnh về đốt sống cổ, số người trong độ tuổi từ 10–20 tuổi chiếm 15%. Người mắc bệnh có tuổi nhỏ nhất chỉ mới tám tuổi và tỉ lệ phát bệnh trong lứa tuổi thanh thiếu niên ngày một cao. Nguyên nhân chủ yếu vẫn là ngồi học trong thời gian dài, tư thế ngồi không đúng, nhất là phải mang cặp (ba lô) quá nặng….Theo một nghiên cứu, học sinh tiểu học và trung học cơ sở nên mang cặp có trọng lượng không được vượt quá 10% trọng lượng cơ thể học sinh.”
Bạn Hải học lớp 7A cân nặng 52kg. Hàng ngày bạn đi học mang một ba lô nặng 4kg. Hôm nay bạn cần đem thêm một số quyển tập mới, mỗi quyển nặng 270g để quyên tặng học sinh vùng khó khăn. Hỏi bạn Hải có thể mang theo nhiều nhất bao nhiêu quyển tập mới để trọng lượng ba lô phù hợp với lời khuyên nói trên.
Câu 5. (1,0 điểm) Để có một ly nước chanh ngon, người ta thường pha các nguyên liệu gồm nước cốt chanh, nước đường và nước lọc theo tỉ lệ 1: 4: 7. Để pha 1,2 lít nước chanh theo công thức đó thì cần bao nhiêu lít nước cốt chanh, bao nhiêu lít nước đường?
Câu 6. (1,0 điểm) Một xí nghiệp dự định giao cho nhóm 48 công nhân thực hiện một dự án trong 12 ngày. Tuy nhiên, khi bắt đầu công việc thì một số công nhân bị điều động đi làm việc khác, do đó thời gian làm việc thực tế của nhóm công nhân còn lại kéo dài thêm 6 ngày so với dự định. Hỏi số công nhân bị điều động đi làm việc khác là bao nhiêu công nhân? (Giả sử năng suất làm việc của mỗi công nhân như nhau).
Câu 7. (3,0 điểm) Cho \[\Delta ABC\] có \[AB = AC\], góc A nhọn. Gọi M là trung điểm của BC. Kẻ BH vuông góc với AC (H Î AC). Trên tia HM, lấy điểm K sao cho M là trung điểm của HK.
a) Chứng minh: \[\Delta MHB = \Delta MKC\]
b) Trên tia đối của tia HB lấy điểm I sao cho HI = HB. Chứng minh: \[IC\,{\rm{//}}HK\]
c) Chứng minh: \[\widehat {BAC} = 2.\widehat {BIC}\]
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 8)
A/ PHẦN TRẮC NGHIỆM: (3,0 điểm)
Câu 1: Chọn câu trả lời đúng: Kết quả phép tính \(\frac{{ - 3}}{8} + \frac{5}{6}\) là:
A. \(\frac{{11}}{{24}}\)
B. \(\frac{{22}}{{48}}\)
C. \(\frac{{ - 11}}{{24}}\)
D. \(\frac{{ - 22}}{{48}}\)
Câu 2: Chọn câu trả lời đúng: Kết quả phép tính 0,75\(.\frac{1}{{ - 3}}\) là:
A. \( - \frac{3}{{12}}\)
B. \( - \frac{1}{4}\)
C. \(\frac{1}{4}\)
D. \(\frac{3}{{12}}\)
Câu 3: Chọn câu trả lời đúng: Cho \(\left| a \right| = \frac{2}{5}\) thì:
A. \[a = \frac{2}{5}\]
B. \[a = - \frac{2}{5}\]
C. \[a = 1\] hoặc \[a = \frac{2}{5}\]
D. \[a = \frac{2}{5}\] hoặc \[a = - \frac{2}{5}\]
Câu 4: Chọn câu trả lời đúng: Kết quả phép tính \({\left( {\frac{{ - 1}}{2}} \right)^3}\) là:
A. \(\frac{1}{6}\)
B. \(\frac{{ - 1}}{6}\)
C. \(\frac{{ - 1}}{8}\)
D. \(\frac{1}{8}\)
Câu 5: Chọn câu trả lời đúng: Cho tam giác ABC. Ta có:
A. \(\angle A + \angle B = {180^0}\)\(\)
B.\(\angle A + \angle B + \angle C = {160^0}\)
C.\(\angle \)\(A + \angle B + \angle C\)= 1\({80^0}\)
D.\(\angle A + \angle B + \angle C\)\(\langle \)\({180^0}\)
Câu 6: Tìm câu trả lời sai: Cho hai tam giác ABC = tam giác DEF (g – c – g ) thì:
A. AB = DE
B.\(\angle C = \angle F\)
C.\(\angle B = \angle E\)
D. BC = EF
B/ PHẦN TỰ LUẬN: (7,0 điểm)
Bài 1: (1,5 điểm). Thực hiện phép tính (bằng cách hợp lý nếu có thể)
a/ \( - 1\frac{1}{2}.21\frac{1}{3} + 1\frac{1}{2}.1\frac{1}{3}\)
b/ \( - {3^2} - {\left( {\frac{1}{2}} \right)^{ - 2}}:{2^2} + {\left( {\frac{2}{3}} \right)^0}:{\left( {\frac{3}{4}} \right)^{ - 1}}\)
c/\(\sqrt {12} + \sqrt {27} - \sqrt 3 \)
Bài 2: (1,5 điểm). Tìm x biết:
a/ \(5\frac{2}{3}x + 1\frac{2}{3} = 4\frac{1}{2}\)
b/ \(\frac{x}{{27}} = \frac{{ - 2}}{9}\)
c/ \(\left| {x - 1,5} \right| = 2\)
Bài 3: (1,5 điểm). Ba ban Lâm, Chí, Dũng có 60 cây bút và số bút tỉ lệ với 3, 4, 5. Tính số bút của mỗi bạn.
Bài 4: (2,0 điểm). Cho góc nhọn xOy, Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.
a/ Chứng minh OAD = OCB
b/ Chứng minh IA = IC
c/ Chứng minh OI là tia phân giác của\(\angle xOy\)
Bài 5: (0,5 điểm) Tìm GTLN của biểu thức: \({\mathop{\rm A}\nolimits} = \left| {x - 1004} \right| - \left| {x + 1003} \right|\).
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 9)
I. TRẮC NGHIỆM (3,0 điểm): Khoanh tròn chữ cái đúng
Câu 1. Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \[ - \frac{3}{4}\]?
A. \[\frac{{ - 6}}{2}\]
B. \[\frac{8}{{ - 6}}\]
C. \[\frac{9}{{ - 12}}\]
D. \[\frac{{ - 12}}{9}\]
Câu 2. Số \[\frac{{ - 5}}{{12}}\] là kết quả của phép tính:
A. \[\frac{{ - 1}}{6} + \frac{{ - 3}}{{12}}\]
B. \[1 - \frac{{ - 7}}{{12}}\]
C. \[\frac{{ - 7}}{{12}} + 1\]
D. \[1 - \frac{7}{{12}}\]
Câu 3/ Nếu \[\sqrt x \]= 9 thì x bằng:
A. 3
B. 6
C. 9
D. 81
Câu 4/ Biết y tỉ lệ thuận với x và khi x = -3 thì y = 1. Khi x = 1 thì y bằng:
A. \[\frac{1}{3}\]
B. \[ - \frac{1}{3}\]
C. 3
D. \[ - 3\]
Câu 5/ Tam giác ABC có, \[\widehat B = \widehat C\], \[\widehat A = {136^ \circ }\]. Góc \[B\] bằng:
A. \[{44^ \circ }\]
B. \[{32^ \circ }\]
C. \[{27^ \circ }\]
D. \[{22^ \circ }\]
Câu 6/ Cách phát biểu nào sau đây diễn đạt đúng tính chất góc ngoài của tam giác:
A. Mỗi góc ngoài của tam giác bằng tổng hai góc trong.
B. Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
C. Mỗi góc ngoài của tam giác bằng tổng ba góc trong.
D.Mỗi góc ngoài của tam giác bằng tổng một góc trong và một góc kề với nó.
II. TỰ LUẬN (7,0 điểm)
Câu 7: (1,0 điểm) thực hiện phép tính: \(\left( {2\frac{2}{3} + 1\frac{1}{3}} \right):\frac{1}{4} - 25\)
Câu 8: (1,0 điểm) Tìm x biết: \(\frac{3}{4} - \left( {x + \frac{1}{2}} \right) = \frac{4}{5}\)
Câu 9: (2,0 điểm) Cho biết 30 công nhân xây xong một ngôi nhà hết 90 ngày. Hỏi 15 công nhân xây ngôi nhà đó hết bao nhiêu ngày? (giả sử năng suất làm việc của mỗi công nhân là như nhau)
Câu 10: (3,0 điểm) Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh:\(\Delta AEC = \Delta BED\)
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 10)
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Hãy viết vào bài làm chữ cái A, B, C hoặc D đứng trước câu trả lời đúng.
Câu 1. Kết quả phép tính \(\frac{{ - 7}}{3}:\sqrt {\frac{{25}}{{36}}} \cdot \frac{{11}}{{12}}\) là:
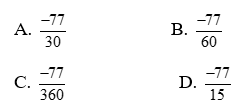
Câu 2. Giá trị của x thỏa mãn \[x.{\left( {\frac{4}{7}} \right)^4} = {\left( {\frac{4}{7}} \right)^6}\] là:
|
A. \(\frac{4}{7}\) |
B. \(\frac{8}{{14}}\) |
C. \(\frac{{16}}{7}\) |
D. \(\frac{{16}}{{49}}\) |
Câu 3. Nếu 15 lít dầu hỏa nặng 12kg thì 24kg dầu hỏa chứa đầy trong thùng:
|
A. 27 lít |
B. 7,5 lít |
C. 30 lít |
D. 15 lít |
Câu 4. Cho \(\Delta {\mathop{\rm ABC}\nolimits} = \,\,\Delta MNP\). Phát biểu nào trong các phát biểu sau đây là sai?
|
A. AB = MN |
B. \(\widehat {\mathop{\rm B}\nolimits} = \widehat {\,N}\) |
C. \(\widehat {\mathop{\rm B}\nolimits} = \widehat {\,P}\) |
D. PM = CA |
Câu 5. Cho tam giác ABC và tam giác MNP có BC = PN, \(\widehat {\mathop{\rm C}\nolimits} = \,\widehat {\mathop{\rm P}\nolimits} \). Thêm một điều kiện nào trong các điều kiện sau để \(\Delta {\mathop{\rm ABC}\nolimits} = \Delta {\mathop{\rm MNP}\nolimits} \) theo trường hợp góc-cạnh-góc:
|
A. BA = NP |
B. \(\widehat {\mathop{\rm B}\nolimits} = \,\widehat {\mathop{\rm N}\nolimits} \) |
C. \(\widehat {\mathop{\rm M}\nolimits} = \,\widehat {\mathop{\rm A}\nolimits} \) |
D. AC=MN |
Câu 6. Cho hình vẽ. Biết a//b. Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B sao cho \(\widehat {{{\mathop{\rm A}\nolimits} _1}} = \,\,2\widehat {{{\mathop{\rm B}\nolimits} _1}}\). Khi đó \(\widehat {{{\mathop{\rm B}\nolimits} _1}}\) bằng:
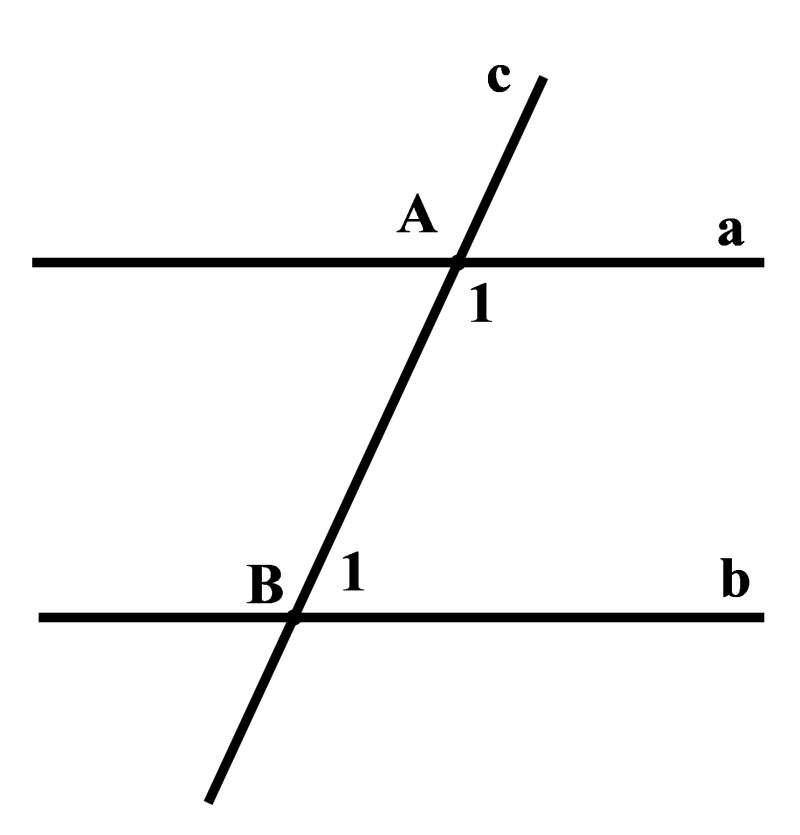
|
A. 60o |
B. 45o |
|
C. 75o |
D. 120o |
II. PHẦN TỰ LUẬN (7,0 điểm)
Câu 7. Tìm x, biết:
a)\(\left( {0,5.x - \frac{3}{7}} \right):\frac{1}{2} = 1\frac{1}{7}\)
b) \(\left| {2 - 3x} \right| - 5 = - 1\)
c) \({\left( {\frac{1}{5} - \frac{3}{2}x} \right)^2} = \frac{9}{4}\)
Câu 8. Ba lớp 7A, 7B và 7C đi lao động và được phân công khối lượng công việc như nhau. Lớp 7A hoàn thành công việc trong 3 giờ, lớp 7B hoàn thành công việc trong 4 giờ và lớp 7C hoàn thành công việc trong 5 giờ. Tính số học sinh của mỗi lớp, biết rằng tổng số học sinh của ba lớp là 94 học sinh (giả sử năng suất làm việc của mỗi học sinh đều như nhau).
Câu 9. Cho tam giác ABC có AB = AC. Vẽ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi I là giao điểm của BD và CE. Chứng minh rằng:
a) BD = CE
b) EI = DI
c) Ba điểm A, I, H thẳng hàng (với H là trung điểm của BC).
Câu 10. So sánh 230 + 330 + 430 và 3.2410
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 11)
I - Phần trắc nghiệm: (3,0 điểm)
Hãy khoanh tròn vào chữ cái trước phương án trả lời đúng:
Câu 1: Nếu \(\sqrt x \) = 2 thì x2 bằng bao nhiêu?
A. 2
B. 16
C. 8
D. 4
Câu 2: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \(\frac{3}{{ - \,4}}\)?
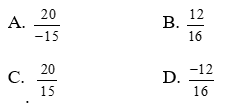
Câu 3: Điểm nào sau đây thuộc đồ thị của hàm số y = – 3x ?
A. Q(\(\frac{2}{3};\,2)\)
B. M(\( - \frac{1}{3};\, - \,1)\)
C. N(\( - \frac{1}{3};\,1)\)
D. P(\(\frac{1}{3};\,1)\)
Câu 4: Hai đường thẳng song song là hai đường thẳng:
A. Có ít nhất 2 điểm chung B. Không có điểm chung
C. Không vuông góc với nhau D. Chỉ có một điểm chung
Câu 5: Giả thiết nào dưới đây suy ra được \(\Delta MNP\,\, = \,\,\Delta M'N'P'\)?
A. \(\hat M\,\, = \,\,\hat M';\,\,MN\, = \,M'N';\,MP\, = \,M'P'\)
B. \(\hat M\,\, = \,\,\hat M';\,\,MP\, = \,M'P';\,NP\, = \,N'P'\)
C. \(\hat M\,\, = \,\,\hat M';\,\,\hat N\,\, = \,\,\hat N';\,\,\hat P\,\, = \,\,\hat P'\)
D. \(\hat M\,\, = \,\,\hat M';\,\,MN\, = \,M'N';\,NP\, = \,N'P'\)
Câu 6: Cho x và y là hai đại lượng tỉ lệ thuận và khi x = 6 thì y = 4. Hệ số tỉ lệ k của y đối với x là:
A. k = 24
B. k = \(\frac{3}{2}\)
C. k = \(\frac{1}{{24}}\)
D. k = \(\frac{2}{3}\)
Câu 7: Nếu tam giác ABC có và \({\rm{A\hat BC}}\,\, = \,\,{\rm{A\hat CB}}\)thì số đo của góc \(A\hat BC\) bằng:
A. 450
B. 650
C. 750
D. 550
Câu 8: Nếu góc xOy có số đo bằng 470 thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?
A. 1330
B. 430
C. 740
D. 470
Câu 9: Kết quả của phép nhân (– 3)6 . (– 3)2 bằng:
A. (– 3)12
B. (– 3)3
C. (– 3)4
D. (– 3)8
Câu 10: Cho x và y là hai đại lượng tỉ lệ nghịch và khi x = – thì y = 4. Hỏi khi x = 2 thì y bằng bao nhiêu?
A. – 1
B. 2
C. 1
D. – 2
Câu 11: Tam giác ABC có = , = 1360. Góc B bằng:
A. 440
B. 320
C. 270
D. 220
Câu 12: Biết y tỉ lệ thuận với x và khi x = -3 thì y = 1. Khi x = 1 thì y bằng:
A. \[\frac{1}{3}\]
B. -\[\frac{1}{3}\]
C. 3
D. -3
II-Phần tự luận: 7,0 điểm
Bài 1: Tính giá trị của các biểu thức sau:
a) \(15\frac{1}{4}\,\,:\,\,( - \,\frac{5}{7})\,\, - \,25\frac{1}{4}\,\,:\,\,( - \,\frac{5}{7})\)
b) \(\sqrt {0,16} \,\, - \,\,\sqrt {0,25} \)
Bài 2: Tìm x, biết:
a) \(\left| {\,x\,\, - \,\,\frac{1}{3}\,} \right|\,\, = \,\,\frac{1}{2}\)
b) \((\frac{1}{3}\,.\,x)\,\,:\,\,\frac{2}{3}\,\, = \,\,4\frac{3}{8}\)
Bài 3: Tính số đo góc A của tam giác ABC biết số đo các góc A, B, C của tam giác đó tỉ lệ với các số 3; 5; 7.
Bài 4: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh: OE là tia phân giác của góc xOy
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 12)
Câu 1. (1,0 điểm)Với hai đại lượng x và y, khi nào y là hàm số của x?
cho hàm số y = f(x) = -2x + 1 hãy tính các giá trị f(-1); f(2).
Câu 2. ( 1,5 điểm) Thực hiện phép tính (một cách hợp lý, nếu có thể):
a) \[\frac{{15}}{{34}} + \frac{7}{{21}} + \frac{{19}}{{34}} - \frac{{20}}{{15}} + \frac{3}{7}\]
b) \[16\frac{2}{7}:\left( { - \frac{3}{5}} \right) - 28\frac{2}{7}:\left( { - \frac{3}{5}} \right)\]
Câu 3. (1,5 điểm) Tìm x và y biết:
a) \[\sqrt x = 3\]
b) \[\left| x \right|\] = 2
c) \[\frac{x}{5} = \frac{y}{{11}}\] và x – y = - 12
Câu 4. (1,5 điểm) Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k, khi x = 4 thì y = 8.
a) Tìm hệ số tỉ lệ k của y đối với x.
b) Biểu diễn y theo x.
c) Tính giá trị của y khi x = 5; x =-10
Câu 5. (2,0 điểm)
a) Nêu tính chất một đường thẳng cắt hai đường thẳng song song.
b) Cho hình vẽ, giải thích vì sao AC//BD?
c)Tìm số đo \(\widehat {ACD}\).
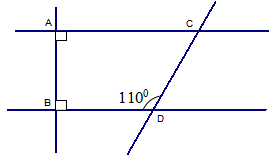
Câu 6. (2,5 điểm) Cho \(\Delta \)ABC có AB = AC, tia phân giác của góc A cắt BC tại H. Chứng minh rằng:
a) HB = HC
b)\(\widehat {ABH} = \widehat {ACH}\)
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Bài thi môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 13)
Câu 1. (2 điểm) Thực hiện phép tính:
a) \[\frac{7}{6} - \frac{1}{6}:\frac{2}{3}\]
b) \[23\frac{1}{4} \cdot \frac{7}{5} - 13\frac{1}{4} \cdot \frac{7}{5}\]
c) \[0,5.\sqrt {100} - \frac{1}{4} \cdot \sqrt {16} + {\left( { - \frac{2}{3}} \right)^2}\]
d) \[\frac{{{3^{27}}}}{{{9^5}\,.\,{3^{16}}}}\]
Câu 2. (2 điểm) Tìm x biết:
a) \[\frac{3}{2}x + \frac{1}{4} = \frac{5}{2}\]
b) \[2\frac{2}{3}:x = 1\frac{7}{9}:0,02\]
Câu 3. (1 điểm) Cho hàm số: \[y = f\left( x \right) = x - 2\]
a) Tính \[f\left( { - 1} \right);\,\,f\left( 0 \right)\].
b) Tìm x để \[f\left( x \right) = 0\].
Câu 4. (1 điểm) Biết ba cạnh của một tam giác tỉ lệ với 2;3;5 và chu vi của nó bằng 45cm.
Tính các cạnh của tam giác đó.
Câu 5. (3 điểm) Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại D.
a) Chứng minh: ADB = ADC.
b) Kẻ DH vuông góc với AB (HÎAB), DK vuông góc với AC (KÎAC). Chứng minh DH = DK
c) Biết . Tính số đo các góc của tam giác ABC
Câu 6. (1 điểm)
Biết \[{1^2} + {2^2} + {3^2} + \ldots + {10^2} = 385\]. Tính tổng sau: \[A = {100^2} + {200^2} + 300{}^2 + \ldots + {1000^2}\]