Tài liệu Bộ đề thi Toán lớp 7 học kì 1 có đáp án năm học 2024 - 2025 gồm 04 đề thi tổng hợp từ đề thi mônToán 7 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 1 Toán lớp 7. Mời các bạn cùng đón xem:

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 1)

A. TRẮC NGHIỆM:          (3 điểm)

Hãy chọn một chữ cái đứng trước câu trả lời mà em cho là đúng ghi vào giấy làm bài :

Câu 1: Tổng 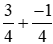 bằng:

Câu 2:  Biết: 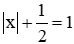 thì x bằng:

Câu 3: Từ tỉ lệ thức 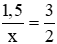 thì giá trị x bằng:

A. 1                     

B. 2                               

C. 3                     

D. 4

Câu 4:  Cho 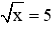 thì  x bằng:

Câu 5: Nếu một đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc...... thì a//b. Cụm từ trong chỗ trống (...) là:

A. so le trong bằng nhau                    

B. đồng vị            

C. trong cùng phía bằng nhau           

D. Cả A, B đều đúng

Câu 6: Cho a ⊥ b và b ⊥ c thì:

A. a//b                 

B. a//c                            

C. b//c                           

D. a//b//c

Câu 7: Cho tam giác ABC có 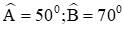. Số đo góc ngoài tại đỉnh C bằng:

A. 60⁰                               

B. 120⁰                                            

C. 70⁰                            

D. 50⁰

Câu 8: Cho ΔABC =  ΔMNP suy ra

A. AB = MP

B. CB = NP       

C. AC = NM                  

D. Cả B và C đúng.

Câu 9: Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ –2 thì y và x liên hệ với nhau theo công thức:

Câu 10: Cho y tỉ lệ nghịch với x theo hệ số tỉ lệ là a, khi x = 3 thì y = 6. Vậy hệ số tỉ lệ a bằng:

A. 2                     

B. 0,5                            

C. 18                   

D. 3

Câu 11: Cho hàm số y = f(x) = 3x + 1.Thế thì  f(-1)  bằng:

A. 2                     

B. – 2                                      

C. 4                     

D. – 4

Câu 12: Trong các điểm sau, điểm nào thuộc đồ thị hàm số y = 2x.

A. (- 1; - 2)           

B. (- 1; 2)                       

C. (- 2: - 1)           

D. ( - 2; 1)

B. TỰ LUẬN:      (7 điểm)

Bài 1: (1,5 điểm)    

Bài 2: (1,5 điểm)    Tính diện tích của một hình chữ nhật biết tỉ số giữa 2 kích thước của chúng là 0,8 và chu vi của hình chữ nhật đó là 36m.

Bài 3: (1,0 điểm)  Vẽ đồ thị hàm số 

Bài 4: (2,5 điểm)  Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.

a) Chứng minh ΔABH = ΔACH

b) Chứng minh AH ⊥ BC

c) Vẽ HD ⊥ AB (D ∈ AB)  và HE ⊥ AC (E ∈ AC). Chứng minh: DE // BC

Bài 5: (0,5 điểm)  Tìm x biết: |2x - 1| + |1 - 2x| = 8

Đáp án và Hướng dẫn làm bài

A. TRẮC NGHIỆM:     (3 điểm)

Mỗi câu  đúng ghi (0,25 điểm) x 12 câu = 3 điểm

Câu 1.

  

Chọn đáp án D

Câu 2.

Chọn đáp án D

Câu 3.

Chọn đáp án A

Câu 4.

Chọn đáp án C

Câu 5.

Theo dấu hiệu nhận biết hai đường thẳng song song: "Nếu một đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì a//b".

Chọn đáp án A

Câu 6.

Ta có: a ⊥ b; b ⊥ c thì a // c (quan hệ giữa tính vuông góc và tính song song)

Chọn đáp án B

Câu 7.

Theo định lý góc ngoài của tam giác, số đo góc ngoài tại đỉnh C là:

  

Chọn đáp án B

Câu 8.

Ta có: ΔABC = ΔMNP

Suy ra: AB = MN; AC = MP; BC = NP (các cạnh tương ứng)

Chọn đáp án B

Câu 9.

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ – 2 thì y và x liên hệ với nhau theo công thức: y = -2x

Chọn đáp án D

Câu 10.

Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ là a nên y = 

Khi x = 3 thì y = 6 nên 6 = 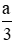 ⇒ a = 6.3 = 18 

Chọn đáp án C

Câu 11.

f(-1) = 3.(-1) + 1 = -3 + 1 = -2

Chọn đáp án B

Câu 12.

+) A(-1; -2)

2. (-1) = -2 nên điểm A thuộc đồ thị hàm số y = 2x.

+) B(-1; 2)

2.(-1) = -2 ≠ 2 nên điểm B không thuộc đồ thị hàm số y = 2x

+) C(-2; -1)

2.(-2) = -4 ≠ -1 nên điểm C không thuộc đồ thị hàm số y = 2x

+) D(-2; 1)

2.(-2) = - 4 ≠ 1 nên điểm D không thuộc đồ thị hàm số y = 2x

Chọn đáp án A

B. TỰ LUẬN:      (7 điểm)

Bài 1.

Bài 2.

Gọi độ dài chiều rộng và chiều dài của hình chữ nhật lần lượt là a, b (m) (a, b > 0)  (0,25 điểm)

Theo đề bài ta có: 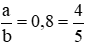 và (a + b).2 = 36         (0,25 điểm)

Suy ra: 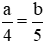 và a + b = 18                                  (0,25 điểm)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   (0,25 điểm)

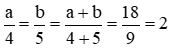
Suy ra: a = 8; b = 10                                

Độ dài chiều rộng và chiều dài của hình chữ nhật lần lượt là 8m và 10m  (0,25 điểm)

Vậy diện tích của hình chữ nhật là: 8. 10 = 80m²  (0,25 điểm)

Bài 3.

Cho x = 3 suy ra y = 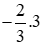 = - 2, ta có A(3; -2)             (0,25 điểm)                                      

Học sinh đánh dấu điểm A và vẽ đồ thị đúng trên mặt phẳng tọa độ Oxy

(0,5 điểm)

Vậy đồ thị hàm số đã cho là đường thẳng OA.  (0,25 điểm)

Bài 4.

Vẽ đúng hình, ghi GT, KL đúng được 0,5 điểm

a) Xét ΔABH và ΔACH có:

  AH cạnh chung

   (AH là tia phân giác của góc BAC)

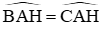
  AB = AC (gt)

Suy ra: ΔABH = ΔACH (c – g – c)               (0,75 điểm)

b)

   (AH là tia phân giác của góc BAC)

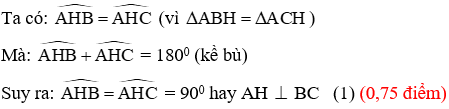
(0,75 điểm)

c) Gọi I là giao điểm của AH và DE

Xét hai tam giác vuông: ΔADH và ΔAEH có:

  AH cạnh chung

   (AH là tia phân giác của góc BAC)

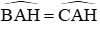
Suy ra: ΔADH = ΔAEH (ch – gn)                               (0,25 điểm)

Xét ΔADI và ΔAEI có:

  AI: cạnh chung

   (AH là tia phân giác của góc BAC)

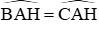
  AD = AE (ΔADH = ΔAEH)

Suy ra: ΔADI = ΔAEI (c – g – c)

Bài 5.

Ta có: |2x - 1| + |1 - 2x| = 8  (1)

Vì 2x – 1 và 1 – 2x là hai số đối nhau, nên: |2x - 1| = |1 - 2x| (2)

Từ (1) và (2) suy ra: 2|2x - 1| = 8 hay |2x - 1| = 4  (0,25 điểm)

Suy ra: 2x – 1 = 4 hoặc 2x – 1 = - 4

.....................Hết.........................

 

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 2)

I. TRẮC NGHIỆM (3,0 điểm)

Hãy chọn phương án trả lời đúng.

Câu 1:  Kết quả phép tính 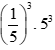  là:

A. 1           

B. 3                     

C. -5           

D. 5

Câu 2:  Cho hàm số 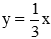 , khi đó hệ số tỉ lệ k là:

A. 1           

B. 3                     

C.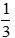             

D. 4

Câu 3:  Cho hình vẽ, ta có:

Câu 4: Cho hình vẽ, ta có:

Câu 5. Kết quả của phép tính 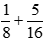  là:

Câu 6. Cho hàm số y = |2x - 1|, giá trị của hàm số tại x = -1 là:

A. 1           

B. -3                    

C. 3            

D. -1

II. TỰ LUẬN (7,0 điểm)

Câu 1: (1,0 điểm) Thực hiện các phép tính sau:

Câu 2: (1,0 điểm)

 Ba đội máy san đất cùng làm một khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 6 ngày, đội thứ hai trong 10 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy (các máy có cùng năng suất), biết đội thứ hai có ít hơn đội thứ ba 3 máy.

Câu 3: (1,0 điểm) 

Cho hàm số y = f(x) = ax    (a ≠ 0)

a) Tìm a biết đồ thị hàm số đi qua điểm A(1; 3)

b) Vẽ đồ thị ứng với giá trị a vừa tìm được.

Câu 4: (1,5 điểm)

Cho hình vẽ:

a) Vì sao m // n ?

b) Tính số đo góc BCD.

Câu 5: (2 điểm)

Cho tam giác ABC vuông ở A. Biết 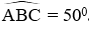 . Lấy điểm M là trung điểm AC. Trên tia đối của tia MB lấy điểm E sao cho MB = ME.

a) Tính số đo góc ACB.

b) Chứng minh ∆AMB = ∆CME.

Câu 6: (0,5  điểm)

Cho 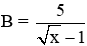. Tìm x ∈ Z để B có giá trị nguyên.

Đáp án và Hướng dẫn làm bài

I. TRẮC NGHIỆM (3 điểm)

Mỗi câu đúng được 0,5 điểm

Câu 1:

Chọn đáp án A

Câu 2:

Chọn đáp án C

Câu 3:

Theo hình vẽ ta có: 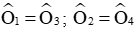 (các góc đối đỉnh)

Chọn đáp án B

Câu 4:

Xét tam giác ABC và tam giác DGE có:

  

Do đó: ΔABC = ΔDEG (c.g.c)

Chọn đáp án D

Câu 5:

Chọn đáp án A

Câu 6:

Thay x = -1 vào hàm số ta được:

y = |2.(-1) - 1| = |-3| = 3

Chọn đáp án C

II. TỰ LUẬN

Câu 1.

Câu 2.

Gọi số máy của 3 độ lần lượt là  x; y; z ( x; y; z ∈ N*)

Theo đề ra ta có: z - y = 3                                              (0,25 điểm)

Vì số máy và thời gian làm việc là hai đại lượng tỉ lệ nghịch nên:

  

Theo tính chất của dãy tỉ số bằng nhau ta có:

  

Vậy số máy của 3 đội lần lượt là: 20; 12; 15 máy.                 (0,25 điểm)

Câu 3.

a) Vì đồ thị hàm số y = ax đi qua điểm A(1; 3) nên: 

3 = a.1 ⇒ a = 3 : 1 = 3

Vậy hàm số là y = 3x với hệ số a = 3.              (0,5 điểm)

b) Đồ thị hàm số y = 3x đi qua A(1; 3)  và O(0; 0).

Vẽ đường thẳng đi qua A(1; 3)  và O(0; 0) ta được đồ thị của hàm số y = 3x.

Vậy đồ thị hàm số y = 3x là đường thẳng OA. (0,5 điểm)

Câu 4.

a) Theo hình vẽ ta có: m ⊥ AB và n ⊥ AB

Do đó: m // n             (0,75 điểm)

b) Vì m // n

Câu 5.

(0,25 điểm)

Chứng minh

a) Áp dụng định lý tổng 3 góc trong tam giác ABC ta có:

b) Xét ∆AMB và ∆CME có:

AM = CM (M là trung điểm của AC)

 (2 góc đối đỉnh)

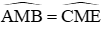
MB = ME (gt)

Do đó: ∆AMB = ∆CME (c.g.c)              (1 điểm)

Câu 6.

Để B có nghĩa thì x ≥ 0 và x ≠ 1

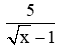
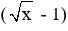
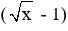
B =   giá trị nguyên khi    là ước của 5.

⇒  ∈ {-5;-1;1;5}                                       (0,25 điểm)

Vậy x ∈ {0; 4; 36} thì B đạt giá trị nguyên.                    (0,25 điểm)

...........................................Hết.....................................

 

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 3)

Bài 1.(1,0 điểm). Hãy viết chữ cái đứng trước phương án trả lời đúng trong các câu sau vào bài làm.

1. Nếu 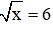  thì x bằng :

A. 6                       

B. -36                          

C. 36                      

D. 12

2. Cho hàm số y = 5x² – 2. Điểm nào sau  đây thuộc đồ thị hàm số trên:

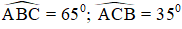
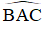
3. Cho ΔABC có . Tia phân giác của  cắt BC tại D.

Số đo 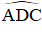 là: 

4. Cho ΔABC = ΔMNP. Biết AB = 10 cm, MP = 8 cm, NP = 7 cm. Chu vi của  là:

A. 30 cm                     

B. 25 cm                  

C. 15 cm              

D. 12,5 cm

Bài 2. (1,0 điểm).  Xác định tính Đúng/Sai của các khẳng định sau:

1.  Nếu x tỉ lệ thuận với y theo hệ số tỉ lệ 2 thì y cũng tỉ lệ thuận với x theo hệ số tỉ lệ là 2.

2. Trên mặt phẳng tọa độ, tất cả các điêm có hoành độ bằng 0 đều nằm trên trục tung.

3. Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

4. Mỗi góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó của tam giác đó.

Bài 3. (2,0 điểm).

Câu 1: Thực hiện các phép tính :

Câu 2: Tìm x biết :

Bài 4. (2,0 điểm).

Câu 1: Để làm một công việc trong 8 giờ cần 35 công nhân. Nếu có 40 công nhân cùng làm thì công việc đó được hoàn thành trong mấy giờ ? (Năng suất các công nhân là như nhau) .

Câu 2: Cho hàm số y = a.x (a ≠ 0). Biết rằng đồ thị của hàm số đó đi qua điểm A(-4; 1).

a.  Hãy xác định hệ số a;

b.  Các điểm M(4 ;-1) và N(2;3) có thuộc đồ thị của hàm số trên không ? Vì sao?

Bài 5.(3,0 điểm).  Cho có AB = AC; D là điểm bất kì trên cạnh AB. Tia phân giác của góc A cắt cạnh DC ở M, cắt cạnh BC ở I.

a) Chứng minh CM = BM.

b)  Chứng minh AI là đường trung trực của đoạn thẳng BC.          

c)  Từ D kẻ DH ⊥ BC (H ∈ BC). Chứng minh .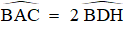

Bài 6. (1,0 điểm) Tìm giá trị nhỏ nhất của biểu thức: A = 3.|1 - 2x| - 5

Đáp án và Hướng dẫn làm bài

Bài 1: (1,0 điểm). Mỗi câu đúng cho 0,25 điểm.

Chọn đáp án C

2. Thay lần lượt tọa độ của các điểm ở đáp án vào hàm số:

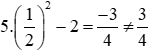
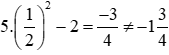
Ta có:   nên điểm A không thuộc đồ thị hàm số y = 5x² - 2

  nên điểm B không thuộc đồ thị hàm số y = 5x² - 2

+) C(2; -18)

5.2² - 2 = 18 ≠ -18 nên điểm C không thuộc đồ thị hàm số y = 5x² - 2

+) D(-1; 3)

5.(-1)² - 2 = 3 nên điểm D thuộc đồ thị hàm số y = 5x² - 2.

Chọn đáp án D

3.

Theo định lý tổng ba góc trong tam giác ABC ta có:

Ta có: 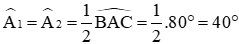  (AD là tia phân giác trong góc BAC)

Lại có góc ADC là góc ngoài tại đỉnh D của tam giác ABD nên theo tính chất góc ngoài của tam giác ta có: 

Chọn đáp án B

4.

Ta có: ΔABC = ΔMNP

Suy ra: AB = MN = 10 cm; BC = NP = 7 cm; AC = MP = 8 cm.

Chu vi tam giác ABC là: AB + BC + AC = 10 + 7 + 8 = 25 cm.

Chọn đáp án B

Bài 2: (1,0 điểm). Mỗi câu đúng cho 0,25 điểm.

1. Nếu x tỉ lệ thuận với y theo hệ số tỉ lệ 2 thì y cũng tỉ lệ thuận với x theo hệ số tỉ lệ là .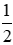

2. Điểm O(0; 0) có hoành độ là 0 vừa thuộc trục hoành, và vừa thuộc trục tung.

3. Đúng theo trường hợp bằng nhau thứ hai của tam giác.

4. Đúng theo định lý góc ngoài của tam giác.

 

  Bài 3. (2,0 điểm).

Câu 1. (1,0 điểm).

Câu 2. (1,0 điểm).

Bài 4. (2,0 điểm).

Câu 1 (1,0 điểm)

Gọi thời gian để 40 công nhân hoàn thành công việc đó là (giờ)  với 0 < x < 8   (0,25 điểm)

Vì cùng làm một công việc và năng suất các công nhân là như nhau nên số công nhân tỉ lệ nghịch với thời gian hoàn thành công việc, do đó ta có:

Vậy 40 công nhân thì hoàn thành công việc đó trong 7 giờ.     (0,25 điểm)

Câu 2( 1,0 điểm)

a)   Vì đồ thị của hàm số y = a.x (a ≠ 0) đi qua điểm A(-4 ;1) nên ta có:

Vậy với 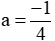 thì đồ thị của hàm số y = a.x (a ≠ 0) đi qua điểm A(-4; 1). (0,25 điểm)

Bài 5. (3,0 điểm).

Vẽ hình đúng, ghi GT, KL đúng (0,5 điểm)

a) Xét ΔABM và ΔACM có:

AB = AC (gt)                                               (0,25 điểm)

  (AI là tia phân giác của góc BAC)        (0,25 điểm)

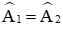
AM cạnh chung                           (0,25 điểm)

Do đó  ΔABM = ΔACM (c.g.c).

Suy ra BM = CM (hai cạnh tương ứng)        (0,25 điểm)

b) Xét ΔABI và ΔACI có:

  AB = AC (gt)

   (AI là tia phân giác của góc BAC)       

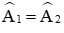
  AI là cạnh chung.     

Do đó ΔABI = ΔACI (c.g.c).(0,25 điểm)

Suy ra BI = CI  (hai cạnh tương ứng).    (1)

và 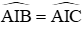 (hai góc tương ứng).                  (0,25 điểm)    

+ Mà 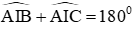 (Vì là hai góc kề bù).   

Nên 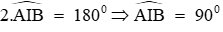 suy ra  AI ⊥ BC  tại I. (2)  (0,25 điểm)

Từ (1) và (2) suy ra AI là đường trung trực của đoạn thẳng BC.  (0, 25 điểm)

c)

+ Ta có: DH ⊥ BC (GT).

  AI ⊥ BC(chứng minh trên)

Suy ra DH // AI (quan hệ giữa tính vuông góc với tính song song )

  ( vì là hai góc đồng vị ).  (3)               (0,25 điểm)

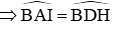
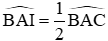
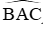
+ Ta lại có:   (vì AI là tia phân giác của ) .(4)

Từ (3) và (4) suy ra 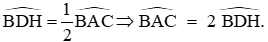 (0,25 điểm)

Bài 6: ( 1,0 điểm ).      

Vậy GTNN của biểu thức A là -5 đạt được khi 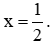.  (0,25 điểm)

......................................Hết.................................

 

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 - Năm học 2024 - 2025

Bài thi môn: Toán lớp 7

Thời gian làm bài: 90 phút

(Đề 4)

 

I. TRẮC NGHIỆM (2 điểm):

Hãy chọn câu trả lời đúng nhất.

Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỷ  ?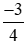

Câu 2: Số 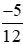 là kết quả của phép tính:

Câu 3: Cho x và y là hai đại lượng tỉ lệ thuận và x = 6 thì y = 4. Hệ số tỉ lệ k của y đối với x là:

Câu 4: Căn bậc hai của 9 bằng:

A. 3                             

B. -3                           

C. 3 và -3                

D. 81

Câu 5: Cách viết nào dưới đây là đúng?

A. |-0,55| = -0,55

B. |-0,55| = 0,55

C. -|-0,55| = 0,55

D. -|0,55| = 0,55

Câu 6: Kết quả của phép tính (-5)².(-5)³ là:

Câu 7: Tam giác ABC có 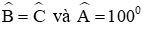. Góc B bằng:

Câu 8: Hai đường thẳng song song là hai đường thẳng:

A. Có ít nhất hai điểm chung.

B. Không có điểm chung.

C. Không vuông góc với nhau.

D. Chỉ có một điểm chung.

II. TỰ LUẬN (8 điểm)

Bài 1 (1,5 điểm): Thực hiện phép tính.

Bài 2 (1,5 điểm): Cho hàm số y = f(x) = (m + 1)x  

     Tìm m để f(2) = 4. Vẽ đồ thị hàm số với m tìm được.

Bài 3 (1,5 điểm): Tìm x, y, z  biết:

Bài 4 (3 điểm): Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của MA lấy điểm K sao cho MK = MA.

a) Chứng minh ΔAMC = ΔKMB và CK song song AB.

b) Biết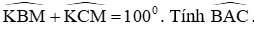   

Bài 5(0,5đ): Cho tam giác ABC. Tia phân giác của góc B cắt AC tại M. Tia phân giác của góc C cắt AB tại N. Giả sử BN + CM = BC. Hãy tính số đó góc A.

Đáp án và Hướng dẫn làm bài

I. PHẦN TRẮC NGHIỆM (2,0 điểm) Mỗi câu đúng được 0,25 điểm

Câu 1.

  

Chọn đáp án C

Câu 2.

  

Chọn đáp án A

Câu 3.

Vì x và y là hai đại lượng tỉ lệ thuận nên ta có y = kx

Với x = 6 thì y = 4 nên thay vào ta được: 4 = k.6 

Chọn đáp án D

Câu 4.

9 có hai căn bậc hai là 

Chọn đáp án C

Câu 5.

Ta có: |-0,55| = 0,55 ; -|-0,55| = -0,55; -|0,55| = -0,55

Chọn đáp án B

Câu 6.

Ta có: (-5)².(-5)³ = (-5)²⁺³ = (-5)⁵

Chọn đáp án A

Câu 7.

Theo định lý tổng ba góc trong tam giác ABC ta có:

Chọn đáp án D

Câu 8.

Hai đường thẳng song song là hai đường thẳng không có điểm chung (định nghĩa hai đường thẳng song song).

Chọn đáp án B

II. PHẦN TỰ LUẬN (8 điểm)

Bài 1.

Bài 2.

a) Ta có f(2) = 4

Thay x = 2 vào hàm số ta được:  (m + 1).2 = 4

⇒  m + 1 = 2 ⇒  m = 1

Vậy m = 1 thì f(2) = 4.                        (0,75 điểm)

b) Với m =1 thì ta có hàm số: y = f(x) = 2x

Lấy x = 1 thì y = 2.1 = 2 nên điểm A(1; 2) thuộc đồ thị hàm số y = 2x

Vậy đồ thị hàm số y = 2x là đường thẳng OA. (0,75 điểm)

Bài 3.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy x =10; y = 6; z = 8                         (0,25 điểm)

Bài 4.

 (0,5 điểm)

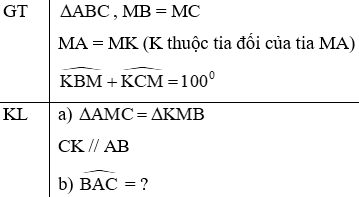
Chứng minh

a)    Xét tam giác  AMC và KMB có:

AM = MK (gt)

MB = MC (M là trung điểm của BC)

 (hai góc đối đỉnh)

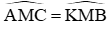
Do đó: ΔAMC = ΔKMB(c.g.c)                   (0,75 điểm)

Chứng minh tương tự ta cũng có: ΔAMB = ΔKMC (c.g.c)               (0,5 điểm)

Suy ra: 

Mà hai góc này ở vị trí so le trong

Nên CK // AB                    (0,5 điểm)

b) Chứng minh được ΔABC = ΔKCB (c.c.c) 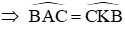 (0,25 điểm)

Xét ΔKBC có:

 (hai góc đối đỉnh)

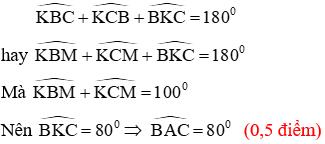
Bài 5.

Gọi BM giao CN là O. Trên cạnh BC lấy điểm E sao cho BN = BE mà BN + CM = BC (gt) ⇒ CE = CM.

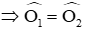
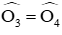
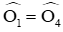
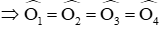
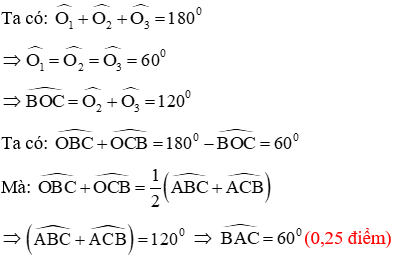
Ta chứng minh ΔBNO = ΔBEO (c.g.c)  . Chứng minh tương tự  . Mà  (hai góc đối đỉnh)   (0,25 điểm)

 (hai góc đối đỉnh)

......................Hết............................