Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 7: Ôn tập chương 3 Hình học có đáp án chi tiết, chọn lọc. Tài liệu có 23 trang gồm 18 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 7. Hi vọng với bộ câu hỏi trắc nghiệm Ôn tập chương 3 Hình học có đáp án này sẽ giúp bạn ôn luyện kiến thức để đạt kết quả cao trong bài thi môn Toán 7 sắp tới.
Giới thiệu về tài liệu:
- Số trang: 23 trang
- Số câu hỏi trắc nghiệm: 18 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Ôn tập chương 3 Hình học có đáp án – Toán lớp 7:
Câu 1: Cho tam giác ABC vuông tại A có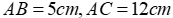 
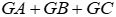
. Gọi G là trọng tâm tam giác ABC, khi đó 
bằng (làm tròn đến 2 chữ số sau dấu phẩy)
A. 11,77 cm
B. 17,11 cm
C. 11,71 cm
D. 17,71 cm
Lời giải:
Gọi AM, BN, CE là ba đường trung tuyến của tam giác ABC
∆ABC vuông tại A nên theo định lí Pytago ta có:
Ta có: AM, BN, CE là các đường trung tuyến ứng với các cạnh BC, AC, AB của tam giác vuông ABC
Suy ra M, N, E lần lượt là trung điểm của các cạnh BC, AC, AB
Áp dụng định lí Pytago với tam giác AEC vuông tại A ta có:
Ta có tam giác ABC vuông tại A, AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
Đáp án cần chọn là: D
Câu 2: Cho tam giác ABC có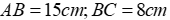 
. Tính độ dài cạnh AC biết độ dài này (theo đơn vị cm) là một số nguyên tố lớn hơn bình phương của 4
A. 17 cm
B. 19 cm
C. 20 cm
D. 17 cm và 19 cm
Lời giải:
+) 
(thỏa mãn bất đẳng thức tam giác)
+) 
(thỏa mãn bất đẳng thức tam giác)
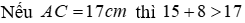
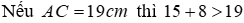
Vậy độ dài cạnh AC có thể là 17 cm và 19 cm
Đáp án cần chọn là: D
Câu 3: Cho tam giác MON, trung tuyến MI, biết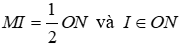 
. Khẳng định nào sau đây đúng?
A. Tam giác MON vuông tại M
B. Tam giác MON vuông tại N
C. Tam giác MON vuông tại O
D. Tam giác MON đều
Lời giải:
Xét tam giác MON có: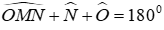 
(định lí tổng ba góc trong tam giác)
Suy ra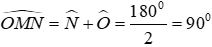 
nên tam giác MON vuông tại M
Đáp án cần chọn là: A
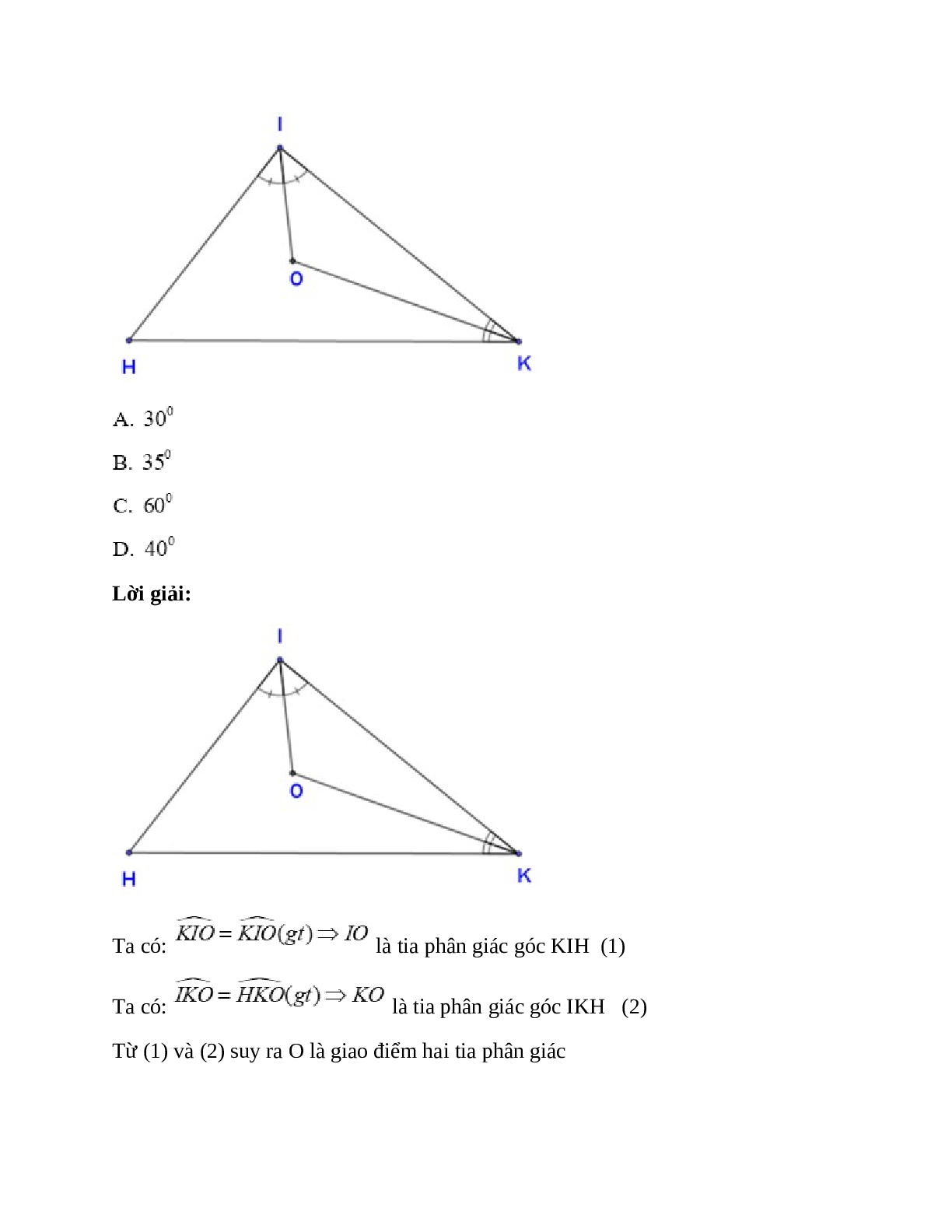
Câu 4: Cho hình vẽ. Biết 
Lời giải:
Ta có: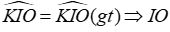 
là tia phân giác góc KIH (1)
Ta có: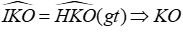 
là tia phân giác góc IKH (2)
Từ (1) và (2) suy ra O là giao điểm hai tia phân giác
Do đó O thuộc tia phân giác của góc H (tính chất ba đường phân giác trong tam giác)
Suy ra: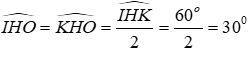 
(tính chất đường phân giác)
Đáp án cần chọn là: A
Câu 5: Cho tam giác vuông MNP như hình vẽ. Trực tam giác MNP là
A. M
B. N
C. P
D. Điểm nằm trong tam giác MNP
Lời giải:
Ta có: MN ⊥ NP nên MN; NP là các đường cao của tam giác MNP mà hai đường này giao nhau tại N nên N là trực tâm tam giác MNP
Đáp án cần chọn là: B
Câu 6: Cho tam giác ABC vuông tại A có BD là phân giác góc ABD (D ∈ AC), kẻ DE vuông góc với BC (E ∈ BC). Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chọn câu đúng
Lời giải:
+) DE vuông góc với BC nên ta có tam giác BDE là tam giác vuông
⇒ B, D nằm trên đường trung trực của AE và BD là đường trung trực của AE. Do đó A đúng
+) Xét hai tam giác vuông ADF và EDC ta có:
Vậy ∆ADF = ∆EDC (hai cạnh góc vuông bằng nhau)
Suy ra DF = DC (hai cạnh tương ứng). Do đó B đúng
+)Trong tam giác vuông ADF, AD là cạnh góc vuông, DF là cạnh huyền nên DA < DF
Mà DF = DC (cmt). Từ đó, suy ra AD < DC. Do đó C đúng
Vậy cả a, b, c đều đúng
Đáp án cần chọn là: D
Câu 7: Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F. Từ B kẻ đường thẳng với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau tại D. Chọn câu sai
Lời giải:
+) Tam giác ABC cân tại A có AM là đường trung tuyến nên AM đồng thời là tia phân giác
Ta có: ME vuông góc với AB tại E nên AEM là tam giác vuông tại E, MF vuông góc với AC tại F nên AMF là tam giác vuông tại F
Xét hai tam giác vuông AEM và AFM có:
Do đó, hai điểm A, M nằm trên đường trung trực EF
Vậy AM là đường trung trực EF
+) Xét hai tam giác vuông ∆ABD vuông tại B, ∆ACD vuông tại C ta có:
AB = AC (do tam giác ABC cân tại A)
AD là cạnh chung
Vậy ∆ABD = ∆ACD (cạnh huyền - cạnh góc vuông)
Suy ra DB = DC (hai cạnh tương ứng bằng nhau)
Do đó D thuộc tia phân giác của góc A (1) (vì điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó)
Lại có AM là tia phân giác của góc A, hay M thuộc tia phân giác của góc A (2)
Từ (1) và (2) suy ra 3 điểm A, M, D thẳng hàng
Ta chưa đủ điều kiện để chỉ ra M là trung điểm của AD
Đáp án cần chọn là: D
Câu 8: Cho tam giác ABC vuông tại A, góc B bằng 60°. Vẽ AH vuông góc với BC tại H. Lấy điểm D thuộc tia đối của tia HA sao cho
8.1: So sánh AB và AC, BH và HC
Lời giải:
+) Tam giác ABC vuông tại A nên ta có:
Trong tam giác ABC ta có 
Xét tam giác ABC vuông tại A có:
BH là hình chiếu của AB trên BC; HC là hình chiếu của AC trên BC
Mà AC > AB (cmt)
Suy ra BH < HC
Đáp án cần chọn là: A
8.2: Tính số đo của góc BDC
Lời giải:
+ Ta có: AH vuông góc với BC tại H và điểm D thuộc tia đối của tia HA nên tam giác AHC vuông tại A, tam giác DHC vuông tại H
Xét hai tam giác vuông AHC và DHC có:
AH = HD (gt)
HC là cạnh chung
Vậy ∆AHC = ∆DHC (hai cạnh góc vuông)
+)Ta có: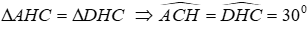 
(hai góc tương ứng) và AC = DC (hai cạnh tương ứng)
Xét hai tam giác ABC và DBC có:
BC cạnh chung
Đáp án cần chọn là: D
Câu 9: Cho tam giác ABC. Gọi O là giao điểm của các đường phân giác của tam giác đó. Từ O kẻ OD,OE,OF lần lượt vuông góc với AB, AC, AB. Trên tia đối của tia AC, BA, CB lấy theo thứ tự ba điểm A1; B1; C1 sao cho AA1 = BC; BB1 = AC; CC1 = AB
9.1: Chọn câu đúng
Lời giải:
+) Do OD, OE, O F lần lượt vuông góc với AB,AC,AB nên các tam giác AOE, AOF, BOF, BOD, COE, COD là các tam giác vuông
O là giao điểm các đường phân giác nên suy ra OD = OE = OF
Xét hai tam giác vuông AOE và AOF ta có:
AO là cạnh chung
OE = OF
Vậy ΔAOE = ΔAOF (cạnh huyền - cạnh góc vuông)
Suy ra AE = AF (hai cạnh tương ứng)
Chứng minh tương tự ta có: BD = BF; CD = CE
Đáp án cần chọn là: A
9.2: Chọn câu đúng
Lời giải:
Đáp án cần chọn là: D
Câu 10: Chọn câu đúng. Cho tam giác ABC vuông tại B theo định lí Pytago ta có:
Lời giải:
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:
Đáp án cần chọn là: B
Câu 11: Chọn đáp án đúng nhất. Tam giác ABC có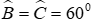 
thì tam giác ABC là tam giác:
A. Cân
B. Vuông
C. Đều
D. Vuông cân
Lời giải:
Áp dụng định lí tổng ba góc trong tam giác ta có
Đáp án cần chọn là: C
Câu 12: Tam giác cân có góc ở đỉnh là 80°. Số đo góc ở đáy là:
Lời giải:
Gỉa sử tam giác ABC cân tại A có: Â = 80°. Ta sẽ tìm số đo góc B hoặc góc C
Áp dụng định lí tổng ba góc trong tam giác ta có:
Đáp án cần chọn là: A
Câu 13: Cho tam giác ABC có: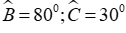 
, khi đó tam giác:
Lời giải:
Áp dụng định lí tổng ba góc trong tam giác ta có:
Tam giác ABC có: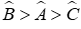 
nên áp dụng quan hệ giữa cạnh và góc trong tam giác suy ra 
Đáp án cần chọn là: B
Câu 14: Chọn đáp án đúng. Cho tam giác ABC có đường cao AH. Biết B nằm giữa H và C. Ta có:
Lời giải:
Vì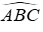 
là góc ngoài tại đỉnh B của tam giác AHB nên:
Hay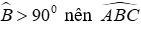 
là góc tù và là góc lớn nhất trong tam giác ABC
Đáp án cần chọn là: B
Câu 15: Cho ∆ABC vuông tại A có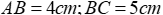 
. So sánh các góc của tam giác ABC
Lời giải:
Vì tam giác ABC vuông tại A nên theo định lí Pytago có:
Đáp án cần chọn là: C
Câu 16: Cho tam giác MNP cân ở M, trung tuyến MA, trọng tâm G. Biết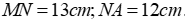 
. Khi đó độ dài MG là:
Lời giải:
Vì ∆MNP cân tại M có MA là trung tuyến nên MA cũng là đường cao (tính chất các đường trong tam giác cân)
Xét ∆MNA vuông tại A, theo định lí Pytago ta có:
Vì MA là trung tuyến, G là trọng tâm nên tính chất trọng tâm tam giác ta có:
Đáp án cần chọn là: D
Câu 17: Cho tam giác ABC, biết số đo các góc tỉ lệ với nhau theo tỉ số: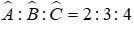 
. Hãy so sánh ba cạnh của tam giác ABC
Lời giải:
Theo bài ra ta có: 
Suy ra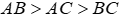 
(quan hệ giữa góc và cạnh đối diện trong ∆ABC)
Đáp án cần chọn là: A
Câu 18: Cho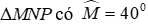 
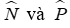
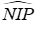
, các đường phân giác NH và PK của 
cắt nhau tại I. Khi đó 
bằng:
Lời giải:
Xét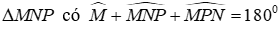 
(định lí tổng ba góc trong một tam giác)
Vì NH là phân giác của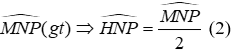 
(tính chất tia phân giác)
Vì PK là phân giác của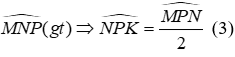 
(tính chất tia phân giác)
Xét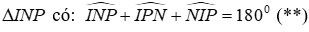 
(định lí tổng ba góc trong tam giác)
Từ (*) và (**) 
Đáp án cần chọn là: C
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
