Tuyển tập đề thi học sinh giỏi toán lớp 9 thành phố Hà Nội

Quý Lê Xuân Ngày: 08-03-2024 Lớp 9

Tải xuống 65 1.1 K 7

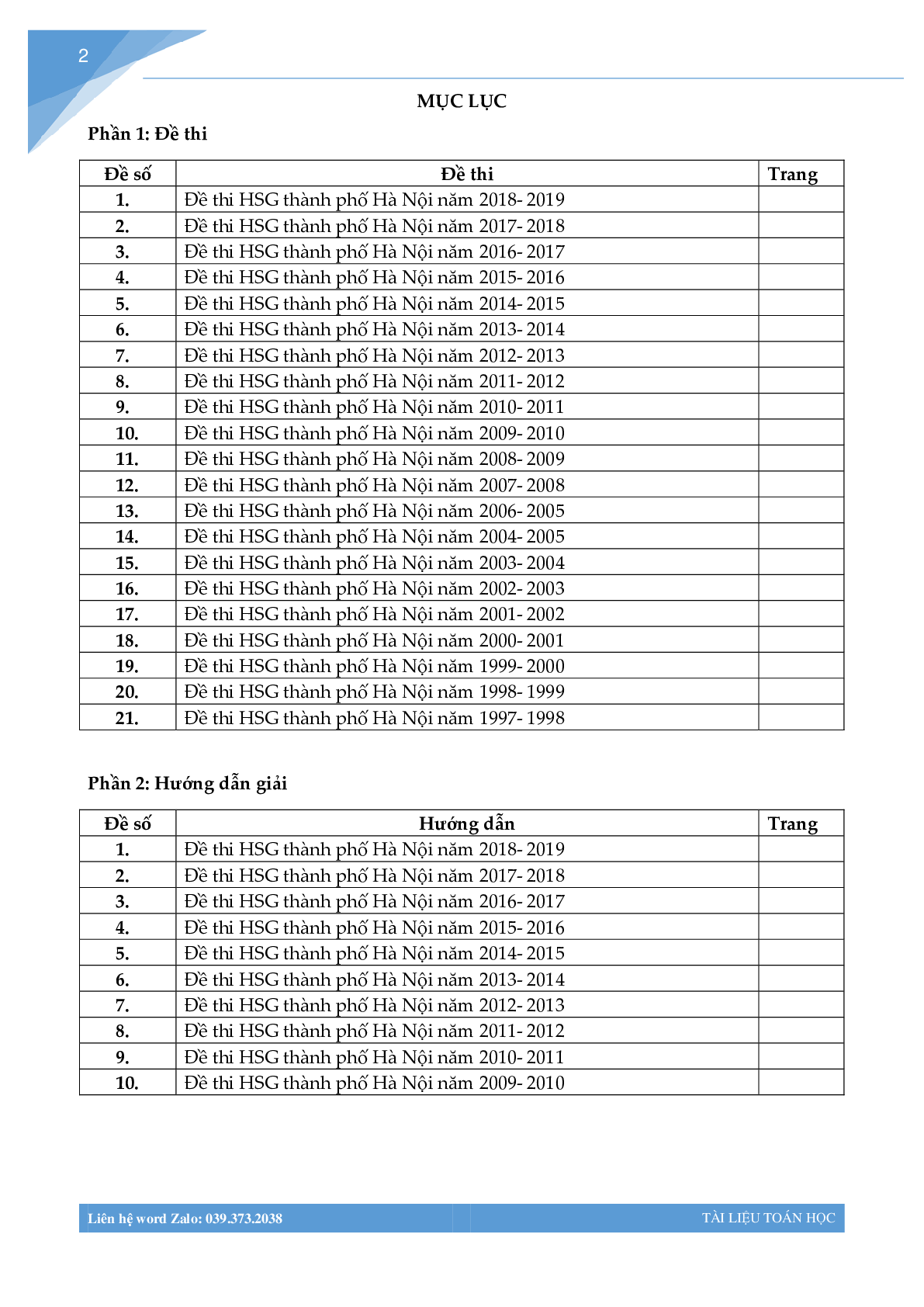
Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đề thi học sinh giỏi toán lớp 9 thành phố Hà Nội, tài liệu bao gồm 65 trang, tuyển chọn Đề thi học sinh giỏi toán lớp 9 thành phố Hà Nội (có đáp án và lời giải chi tiết – nếu có), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

KÌ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 9 THCS NĂM HỌC 2018 – 2019
MÔN THI: TOÁN

Câu 1: (5,0 điểm)
a) Giải phương trình: $\sqrt[3]{2 - x} = 1 - \sqrt{x - 1}$

b) Cho $S = (1 - \frac{2}{2.3}) (1 - \frac{2}{3.4}) . . . (1 - \frac{2}{2020.2021})$ là một tích của 2019 thừa số. Tính S (kết quả để dưới dạng phân số tối giản).

Câu 2: (5,0 điểm)

a) Biết a; b là các số nguyên dương thỏa mãn $a^{2} - a b + b^{2}$ chia hết cho 9, chứng minh rằng cả a và b đều chia hết cho 3.

b) Tìm tất cả các số nguyên dương n sao cho $9^{n} + 11$ là tích của k $(K \in N, k \geq 2)$ số tự nhiên liên tiếp.

Câu 3: (3,0 điểm)

a) Cho x; y; z là các số thực dương nhỏ hơn 4 . Chứng minh rằng trong các số $\frac{1}{x} + \frac{1}{4 - y}, \frac{1}{y} + \frac{1}{4 - z}, \frac{1}{z} + \frac{1}{4 - x}$ luôn tồn tại ít nhất một số lớn hơn hoặc bằng 1.

b) Với các số thực dương a, b, c thay đổi thỏa mãn điều kiện $a^{2} + b^{2} + c^{2} + 2 a b c = 1,$ tìm giá trị lớn nhất của biểu thức P=ab+bc+ca-abc

Câu 3: (6,0 điểm) Cho tam giác ABC vuông tại A (AB<AC). Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh
BC, CA, AB lần lượt tại D, E, F. Gọi S là giao điểm của AI và DE .

a) Chứng minh rằng tam giác IAB đồng dạng với tam giác EAS .

b) Gọi K là trung điểm của AB và O là trung điểm của
.BC Chứng minh rằng ba điểm K, O, S thẳng hàng.

c) Gọi M là giao điểm của KI và AC. Đường thẳng chứa đường cao AH của tam giác ABC cắt đường thẳng DE tại N . Chứng minh rằng AM = AN .

Câu 4: (1,0 điểm) Xét bảng ô vuông cỡ 10 x 10 gồm 100 hình vuông có cạnh 1 đơn vị. Người ta điền vào mỗi ô vuông của bảng một số nguyên tùy ý sao cho hiệu hai số được điền ở hai ô chung cạnh bất kỳ đều có giá trị tuyệt đối không vượt quá 1. Chứng minh rằng tồn tại một số nguyên xuất hiện trong bảng ít nhất 6 lần.

Xem thêm