Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 1 Bài 10: Chia đơn thức cho đơn thức. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 10: Chia đơn thức cho đơn thức. Mời các bạn đón xem:
Bài tập Toán 11 Chương 1 Bài 10: Chia đơn thức cho đơn thức
A. Bài tập Chia đơn thức cho đơn thức.
I. Bài tập trắc nghiệm
Bài 1: Kết quả nào sau đây đúng?
A. (10xy2) : (2xy) = 5xy
B. (-x4y5z) : (x3y2z) = xy3
C. (-xy2)2 : (x2y3) = y
D. (-3x2y2z) : (-yz) = -3x2y
Lời giải:
Ta có:
+
⇒ Đáp án A sai.
+
⇒ Đáp án B sai.
+
⇒ Đáp án C đúng.
+
⇒ Đáp án D sai.
Chọn đáp án C.
Bài 2: Kết quả của phép tính ( - 3 )6 : (- 2 )3 là ?
A.
B.
C.
D.
Lời giải:
Ta có: ( - 3 )6 : ( - 2 )3 = 36:( - 23 ) = 729:( - 8 ) =
Chọn đáp án C.
Bài 3: Giá trị của biểu thức A = ( xy2)3 : ( xy )3 tại x= -1, y =1 là ?
A. A= -1
B. A= 1
C. A= 0
D. A= 2
Lời giải:
Ta có A = ( xy2)3 :( xy )3 = ( x3y6 ):( x3y3 ) = y3
Với x= -1, y =1 ta có A = 13 = 1.
Chọn đáp án B.
Bài 4: Rút gọn biểu thức: A = 210 : (-2)5
A. 32
B. – 32
C. – 4
D. 4
Lời giải:
Ta có: (-2)5 = (-1.2)5 = (-1)5 . 25 = -25
Do đó: A = 210 : (-25) = 210 : (-25) = -210 – 5 = -25 = -32
Chọn đáp án B
Bài 5: Tính (-7)20 : (-7)18
A. 49
B. –49
C. – 14
D. 14
Ta có: (-7)20 : (-7)18 = (-7)20 – 18 = (-7)2 = 49
Chọn đáp án A
Bài 6: Tính x17 : (-x)8
A. –x8
B. x11
C. –x9
D. x9
Ta có: (-x)8 = (-1.x)8 = (-1)8.x8 = x8
Do đó x17 : (-x)8 = x17 : x8 = x9
Chọn đáp án D
Bài 7: Tính
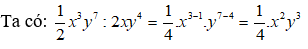
Chọn đáp án A
Bài 8: Tính
A. 2x2y3
B. y2
C. 2x2y5
D. x2y3
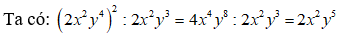
Chọn đáp án C
Bài 9: Tính
A. –xy
B. –x2y2
C. -3xy
D. 3x3y4
Lời giải:
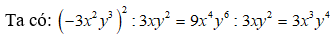
Chọn đáp án D
Bài 10: Tính
Lời giải:
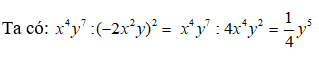
Chọn đáp án A
Bài 11: Kết quả của phép chia (2x3 – x2 +10x) : x là
A. x2 – x + 10
B. 2x2 – x + 10
C. 2x2 – x – 10
D. 2x2 + x + 10
Lời giải:
Ta có (2x3 – x2 +10x) : x
= (2x3 : x) – (x2 : x) + (10x : x) = 2x2 – x + 10
Đáp án cần chọn là: B
Bài 12: Kết quả của phép chia (6xy2 + 4x2y – 2x3) : 2x là
A. 3y2 + 2xy – x2
B. 3y2 + 2xy + x2
C. 3y2 – 2xy – x2
D. 3y2 + 2xy
Lời giải:
(6xy2 + 4x2y – 2x3) : 2x
= 6xy2 : 2x + 4x2y : 2x – 2x3 : 2x
= 3y2 + 2x – x2
Đáp án cần chọn là: A
Bài 13: Chia đa thức (3x5y2 + 4x3y2 – 8x2y2) cho đơn thức 2x2y2 ta được kết quả là?
A. x3 + 2x
B. x3 + 2x - 4
C. x3 + 2x - 4
D. x3y + 2xy - 4
Lời giải:
Ta có (3x5y2 + 4x3y2 – 8x2y2) : 2x2y2
= (3x5y2 : 2x2y2) + (4x3y2 : 2x2y2) – (8x2y2 : 2x2y2)
= x3 + 2x - 4
Đáp án cần chọn là: B
Bài 14: Chia đa thức (4x2yz4 + 2x2y2z2 – 3xyz) cho đơn thức xy ta được kết quả là
A. 4xz4 + 2xyz2 – 3z
B. 4xz4 + 2xyz2 + 3z
C. 4xz4 – 2xyz2 + 3z
D. 4xz4 + 4xyz2 + 3z
Lời giải:
Ta có (4x2yz4 + 2x2y2z2 – 3xyz) : xy
= (4x2yz4 : xy) + (2x2y2z2 : xy) – (3xyz : xy)
= 4xz4 + 2xyz2 – 3z
Đáp án cần chọn là: A
Bài 15: Chọn câu đúng
A. 24x4y3 : 12x3y3 = 2xy
B. 18x6y5 : (-9x3y3) = 2x3y2
C. 40x5y2 : (-2x4y2) = -20x
D. 9a3b4x4 : 3a2b2x2 = 3ab3x2
Lời giải:
Ta có
+) 24x4y3 : 12x3y3 = (24 : 12).(x4 : x3).(y3 : y3) = 2x nên A sai
+) 18x6y5 : (-9x3y3) = (18 : (-9)).(x6 : x3).(y5 : y3)= -2x3y2 nên B sai
+) 40x5y2 : (-2x4y2) = (40 : (-2)).(x5 : x4).(y2 : y2) = -20x nên C đúng
+) 9a3b4x4 : 3a2b2x2 = (9 : 3).(a3 : a2).(b4 : b2).(x4 : x2) = 3ab2x2 nên D sai
Đáp án cần chọn là: C
II. Bài tập tự luận
Bài 1: Làm tính chia:
a) x10 : (-x)8;
b) (-x)5 : (-x)3;
c) (-y)5 : (-y)4.
Lời giải:
a) x10 : (-x)8 = x10 : x8 = x10 – 8 = x2
b) (-x)5 : (-x)3= (-x)5 – 3 = (-x)2 = x2
c) (-y)5 : (-y)4 = (-y)5 – 4 = -y
Bài 2: Chứng mình rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = x2y3:(- xy) + 2x(y - 1)(y + 1)
Lời giải:
Ta có A = x2y3:(xy) + 2x(y - 1)(y + 1) = - 2x2 - 1y3 - 1 + 2x(y - 1)(y + 1)
= - 2xy2 + 2x(y2 - 1) = - 2xy2 + 2xy2 - 2x = - 2x
⇒ Giá trị của biểu thức A không phụ thuộc vào biến y.
Bài 3: Tính giá trị của biểu thức 15x4y3z2 : 5xy2z2 với x = 2, y = -10, z = 2004
Lời giải:
15x4y3z2 : 5xy2z2 với x = 2, y = -10, z = 200
Ta có 15x4y3z2 : 5xy2z2 = 3 . x4 – 1 . y3 – 2 . z2 – 2 = 3x3y
Tại x = 2, y = -10, z = 2004
Ta được: 3 . 23(-10) = 3 . 8 . (-10) = -240.
Bài 4: Làm tính chia:
a, x2yz : xyz
b, x3y4 : x3y
Lời giải:
a, x2yz : xyz = (x2 : x)(y : y)(z : z) = x
b, x3y4 : x3y = (x3 : x3)(y4 : y) = y3
Bài 5: Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết:
a, x4 : xn
b, xn : x3
c, 5xny3 : 4x3y2
d, xnyn+1 : x2y5
Lời giải:
a, x4 : xn = x4-n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4
suy ra: n ∈ {0; 1; 2; 3; 4}
b, xn : x3 = xn- 3 là phép chia hết nên n – 3 ≥ 0 ⇒ n ≥ 3
c, 5xny3 : 4x3y2 = 54 (xn : x2)(y3 : y2) = 54 xn-2 là phép chia hết
Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2
d, xnyn + 1 : x2y5 = (xn : x2)(yn+1 : y5) = xn-2.yn-4 là phép chia hết
suy ra: n – 4 ≥ 0 ⇒ n ≥ 4
Bài 6: Tính giá trị của biểu thức sau:
(- x2y5)2 : (- x2y5) tại x = và y = - 1
Lời giải:
Ta có: (- x2y5)2 : (- x2y5) = - x2y5
Thay x = và y = - 1 vào biểu thức ta được:
-()2.(-1)5 = - .(-1) =
Bài 7: Giá trị của biểu thức A = (xy2)3:(xy)3 tại x= -1, y =1 là?
Lời giải:
Ta có A = (xy2)3:(xy)3 = (x3y6):(x3y3) = y3.
Với x= -1, y =1 ta có A = 13 = 1.
Bài 8: Tính giá trị của các biểu thức sau
a) P = 12x4y2:(- 9xy2) tại x= -3, y= 1,005.
b) Q = 3x4y3:2xy2 tại x= 2, y= 1.
Lời giải:
a) Ta có P = 12x4y2:(- 9xy2) = - 9x4 - 1y2 - 2 = - x3
Với x= -3, y= 1,005 ta có P = - (- 3)3 = 36.
Vậy P = 36
b) Ta có Q = 3x4y3:2xy2 = x4 - 1y3 - 2 = x3y.
Với x= 2, y= 1 ta có Q = ( 2 )3.1 = 12.
Vậy Q = 12
Bài 9: Rút gọn rồi tính giá trị của biểu thức P = 15x4y2 : (-3xy2) tại x = -2, y = 1.
Lời giải:
Ta có: P = 15x4y2 : (-3xy2) = -5x3y0 = -5x3 (Lưu ý: y0 = 1)
Thay x = -2, y = 1 ta được:
P = -5.(-2)3 = -5. (-8) = 40
Bài 10: Tính giá trị của biểu thức 32x6y5z10 : 8x4y3z10 với x = 3, y = 2, z = 1996
Lời giải:
32x6y5z10 : 8x4y3z10
= 4x6-4y5-3z10-10
= 4x2y2
= 4.32.22
=144
III. Bài tập vận dụng
Bài 1: Làm phép tính chia các biểu thức sau:
a) 43 : (-4)2;
b) ()5: ()3
c) (-12)3 : 83.
Bài 2: Tìm số tự nhiên n để phép chia sau là phép chia hết: 4xnyn+1 : 3x4y6.
Bài 3: Chia đơn thức (-3x)5 cho đơn thức (-3x)2 ta được kết quả là?
Bài 4: Giá trị số tự nhiên n để phép chia xn : x6 thực hiện được là?
Bài 5: Tìm điều kiện của số tự nhiên n (n > 0) để đơn thức B = 4x4y4 chia hết đơn thức C = xn-1y4 là?
Bài 6: Rút gọn biểu thức: A = 210 : (-2)5.
Bài 7: Tính x17 : (-x)8
Bài 8: Tìm số tự nhiên n (n>0) để A chia hết cho B?
A = 4x4y4 , B = xn-1y4
Bài 9: Tìm n thuộc N* để 15xn+2y8 chia hết cho x8yn?
Bài 10: Chứng minh rằng biểu thức A = (-15x3y6) : (-5xy2) không âm với mọi giá trị của biến.
B. Lý thuyết Chia đơn thức cho đơn thức.
Khái niệm: Cho A và B là hai đơn thức, B ≠ 0.
Ta nói đơn thức A chia hết cho đơn thức B nếu tìm được một đơn thức Q sao cho
A = B.Q
A được gọi là đơn thức bị chia, B được gọi là đơn thức chia, Q được gọi là đơn thức thương.
Kí hiệu: Q = A : B hoặc .
Nhận xét: Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Quy tắc: Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:
- Chia hệ số của đơn thức A cho hệ số của đơn thức B.
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được với nhau.
Chú ý: Với mọi x ≠ 0, m, n ∈ ℕ, m ≥ n thì
xm : xn = xm – n nếu m > n
xm : xn = 1 nếu m = n.
Ví dụ:
a) 15x2y5z : 5xy3z = (15 : 5)(x2 : x)(y5 : y3)(z : z) = 3xy2.
b) 35x5y2 : (−7x4y) =[35 : (−7)](x5 : x4)(y2 : y) = −5xy.

