Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề Đạo hàm môn Toán lớp 11 có lời giải chi tiết, tài liệu bao gồm 28 trang giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi môn Hóa học sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Chuyên đề Đạo hàm hay, chọn lọc

I. ĐẠO HÀM TẠI MỘT ĐIỂM

1. Định nghĩa đạo hàm tại một điểm

    Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Nếu tồn tại giới hạn (hữu hạn)

    

thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x₀ và kí hiệu là f’(x₀) (hoặc y’(x₀)), tức là

    

Chú ý:

    Đại lượng Δx = x – x₀ gọi là số gia của đối số x tại x₀.

    Đại lượng Δy = f(x) – f(x₀) = f(x₀ + Δx) – f(x₀) được gọi là số gia tương ứng của hàm số. Như vậy

2. Cách tính đạo hàm bằng định nghĩa

    Bước 1. Giả sử Δx là số gia của đối số x tại x₀, tính Δy = f(x₀ + Δx) – f(x₀).

3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

Định lí 1

    Nếu hàm số y = f(x) có đạo hàm tại x₀ thì nó liên tục tại x₀.

Chú ý:

    a) Nếu y = f(x) gián đoạn tại x₀ thì nó không có đạo hàm tại x₀.

    b) Nếu y = f(x) liên tục tại x₀ thì có thể không có đạo hàm tại x₀.

4. Ý nghĩa hình học của đạo hàm

Định lí 2

    Đạo hàm của hàm số y = f(x) tại điểm x₀ là hệ số góc của tiếp tuyến M₀T của đồ thị hàm số tại điểm M₀(x₀; f(x₀)).

Định lí 3

    Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là

        y – y₀ = f’(x₀)(x – x₀)

    trong đó y₀ = f(x₀).

5. Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời: v(t₀) = s’(t₀).

Cường độ tức thời: I(t₀) = Q’(t₀).

II. ĐẠO HÀM TRÊN MỘT KHOẢNG

Định nghĩa

    Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.

    Khi đó, ta gọi hàm số f’: (a; b) → R

    x → f’(x)

    là đạo hàm của hàm số y = f(x) trên khoảng (a; b), kí hiệu là y’ hay f’(x).

III. Các dạng bài tập

Dạng 1: Tìm số gia của hàm số

Phương pháp giải:

Để tính số gia của hàm số y = f(x) tại điểm x₀ tương ứng với số gia ∆x cho trước ta áp dụng công thức: ∆y = f(x₀ + ∆x) − f(x₀).

Ví dụ minh họa:

Ví dụ 1: Tìm số gia của hàm số y = f(x) = x³ – 3x² + 2, biết rằng:

a) x₀ = 1; ∆x = 1

b) x₀ = 1; ∆x = −0,1

Lời giải

a) Số gia của hàm số là: 

∆y = f(x₀ + ∆x) − f(x₀) = f(2) − f(1)

= 2³ − 3.2² + 2 − (1³ −  3.1² +2) = − 2

.b) Số gia của hàm số là: 

∆y = f(x₀ + ∆x) − f(x₀) = f(0,9) − f(1)

= 0,9³ − 3.0,9² +2 − (1³ −  3.1² +2) = 0,299.

Ví dụ 2: Tìm số gia của hàm số:

a) y = 2x + 3

b) y = 2x² – 3x + 1 tại x₀ = 1

Lời giải

a) Số gia của hàm số là: 

∆y = f(x₀ + ∆x) − f(x₀) 

= 2(x₀ + ∆x) + 3 − (2x₀ + 3) = 2∆x

b) Số gia của hàm số là:

∆y = f(1 + ∆x) − f(1)

= 2(1 + ∆x)² − 3(1 + ∆x) + 1 − (2.1² − 3.1 +1)

= 2 + 4∆x + 2(∆x)² − 3 − 3∆x +1 − 0

= 2(∆x)² + ∆x.

Dạng 2: Tính đạo hàm bằng định nghĩa

Phương pháp giải: 

Muốn tính đạo hàm của hàm số tại điểm x₀ theo định nghĩa, ta có 2 cách:

Cách 1: 

Bước 1: Với ∆x là số gia của đối số tại x₀ ta tính ∆y = f(x₀ + ∆x) − f(x₀)

Bước 2: Tính giới hạn 

Cách 2: Đạo hàm của hàm số tại x₀ là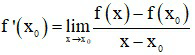  

Chú ý: Nếu không tồn tại giới hạn hữu hạn tại x₀ thì hàm số không có đạo hàm tại x₀.

Ví dụ minh họa:

Ví dụ 1: Tính đạo hàm (bằng định nghĩa) của các hàm số sau:

a) y = 2x² + x + 1 tại x₀ = 2.

b) 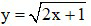tại x₀ = 1.

c) 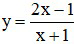 tại x₀ = 3

Lời giải

a) Cách 1: Với  là số gia của đối số x₀ = 2. 

Khi đó hàm số số gia tương ứng:

∆y = f(x₀ + ∆x) − f(x₀)

= 2(2 + ∆x)² + (2 + ∆x) + 1 − (2.2² − 2 +1)

= 8 + 8∆x + 2(∆x)² + 2 + ∆x +1 − 11

= 9∆x + 2(∆x)² = ∆x(9 + 2∆x) .

Ta có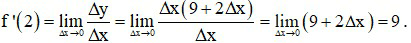  

Cách 2: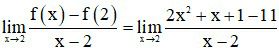  

 

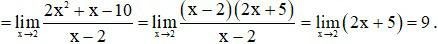
Kết luận theo định nghĩa, hàm số có đạo hàm tại x₀ = 2 và f '(2) = 9.

b) Cách 1: Với ∆x là số gia của đối số x₀ = 1. 

Khi đó hàm số số gia tương ứng:

∆y = f(x₀ + ∆x) − f(x₀) = f(1 + ∆x) − f(1)

 

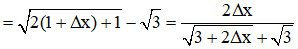
Ta có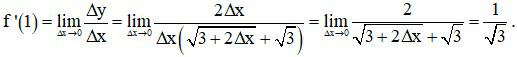  

Cách 2: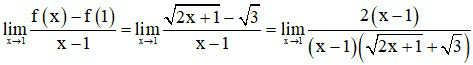  

Kết luận theo định nghĩa, hàm số có đạo hàm tại x₀ = 1 và  .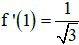

c) Cách 1: Với  là số gia của đối số x₀ = 3. 

Khi đó hàm số số gia tương ứng:

∆y = f(x₀ + ∆x) − f(x₀) = f(3 + ∆x) − f(3)

Ta có  .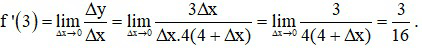

Cách 2: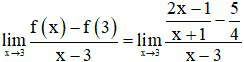  

 

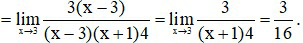
.Kết luận theo định nghĩa, hàm số có đạo hàm tại x₀ = 3 và  .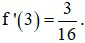

Ví dụ 2: Tính đạo hàm (bằng định nghĩa) của các hàm số sau:

a) y = x³ tại x₀

b) 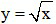tại x₀ 

Lời giải

a) Với  là số gia của đối số x₀. 

Khi đó hàm số số gia tương ứng:

∆y = f(x₀ + ∆x) − f(x₀) = (x₀ + ∆x)³ − x₀³

= x₀³ + 3x₀²∆x + 3x₀.(∆x)² + (∆x)³ − x₀³

= 3x₀²∆x + 3x₀.(∆x)² + (∆x)³

Ta có: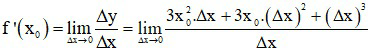  

Vậy đạo hàm của hàm số tại x₀ là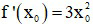  

b) Với ∆x là số gia của đối số x₀. 

Khi đó hàm số số gia tương ứng:

∆y = f(x₀ + ∆x) − f(x₀) =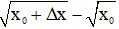  

Ta có: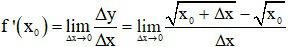  

 

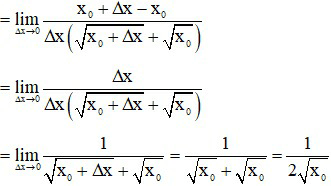
Dạng 3: Mối liên hệ giữa đạo hàm và tính liên tục của hàm số

Phương pháp giải: 

Định lí: Nếu hàm số f(x) có đạo hàm tại x₀ thì f(x) liên tục tại x₀.

Chú ý: Nếu hàm số không liên tục tại x₀ thì không có đạo hàm tại x₀.

Ví dụ minh họa:

Ví dụ 1: Hàm số y = f(x) = |x| liên tục tại x = 0 nhưng không tồn tại đạo hàm tại x = 0:

Lời giải

Ta có: 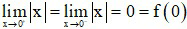 nên hàm số f(x) = |x| liên tục tại x = 0. 

Ta có: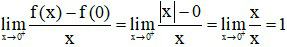  

 

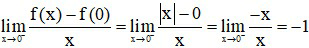
Nên 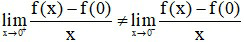 nên hàm số không có đạo hàm tại x = 0.

IV. Bài tập tự luyện

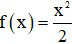
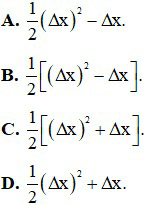
Câu 1. Số gia của hàm số  ứng với số gia ∆x của đối số x tại x₀ = – 1 là

 

Câu 2. Tỉ số 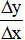 của hàm số f(x) = 2x(x – 1) theo x và ∆x là

A. 4x +2∆x +2.                                       

B. 4x + 2(∆x)² − 2.

C. 4x + 2∆x − 2.                                     

D. 4x∆x + 2(∆x)² − 2∆x.

Câu 3. Số gia của hàm số f(x) = x³ ứng với x₀ = 2 và ∆x = 1 bằng bao nhiêu?

A. – 19 .                B. 7 .                         C. 19.                        D. –7.

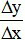
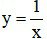
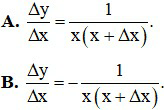
Câu 4. Tính tỷ số  của hàm số  theo x và ∆x

 

Câu 5. Đạo hàm của hàm số f(x) = 2x + 1 tại x₀ = 1

A. 2                       B. 3                           C. 4                           D. 5

Câu 6. Đạo hàm của hàm số f(x) = x³ tại x₀ = 1

A. 4                       B. 3                           C. 5                           D. 6

Câu 7. Đạo hàm của hàm số y = x³ + x – 2 tại x₀ = – 2 là

A. 13.                     B. 12.                       C. 10.                        D. – 8.

Câu 8. Đạo hàm của hàm số 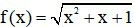 tại điểm x₀ = 2

 

Câu 9. Đạo hàm của hàm số 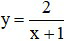 tại x₀ = 2 là

 

Câu 10. Đạo hàm của hàm số 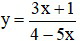 tại x₀ = 1 là

A. 15.                    B. – 15.                     C. – 17.                     D. 17.

Câu 11. Đạo hàm của hàm số 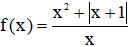 tại x₀ = – 1.

A. 2                       B. 0                           C. 3                           D. Đáp án khác

Câu 12. Đạo hàm của hàm số f(x) = x² – x tại điểm x₀ ứng với số gia ∆x là:

Câu 13. Cho hàm số 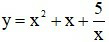 . Khẳng định nào là đúng:

A. Hàm số liên tục trên R, không có đạo hàm trên R.

B. Hàm số liên tục trên R, có đạo hàm trên R.

C. Hàm số không liên tục trên R, không có đạo hàm trên R.

D. Hàm số không liên tục trên R, có đạo hàm trên R.

Câu 14. Cho hàm số y = |2x – 3|. Khẳng định nào là đúng:

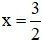
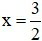
A. Hàm số liên tục tại  , không có đạo hàm tại  .

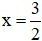
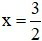
B. Hàm số liên tục tại  , có đạo hàm tại  .

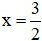
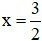
C. Hàm số không liên tục tại  , không có đạo hàm tại  .

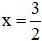
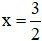
D. Hàm số không liên tục tại  , có đạo hàm tại  .

Câu 15. Cho hàm số y = f(x) =x² - 2|x + 3|. Khẳng định nào là đúng:

A. Hàm số liên tục trên R, không có đạo hàm trên R.

B. Hàm số liên tục trên R, có đạo hàm trên R.

C. Hàm số không liên tục trên R, không có đạo hàm trên R.

D. Hàm số không liên tục trên R, có đạo hàm trên R.

Bảng đáp án