Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Hàm số - Đồ thị hàm số Toán lớp 7, tài liệu bao gồm 17 trang, tuyển chọn bài tập Hàm số - Đồ thị hàm số đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Hàm số - Đồ thị hàm số gồm các nội dung chính sau:

A. Phương pháp giải

- tóm tắt lý thuyết ngắn gọn.

B. Một số ví dụ

- gồm 10 ví dụ minh họa đa dạng của các dạng bài tập Hàm số - Đồ thị hàm số có lời giải chi tiết.

C. Bài tập vận dụng

- gồm 15 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng bài tập Hàm số - Đồ thị hàm số.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

HÀM SỐ - ĐỒ THỊ CỦA HÀM SỐ

A. Phương pháp giải

1. Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

2. Khi y là hàm số của x ta có thể viết $y=f\left(x\right),y=g\left(x\right)\mathrm{...}$

Tập xác định của hàm số là tập hợp tất cả các giá trị của biến số.

Hàm số có thể được cho bằng bảng, bằng công thức, bằng sơ đồ mũi tên, bằng đồ thị.

Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng.

3. Mặt phẳng tọa độ Oxy được xác định bởi hai trục số vuông góc với nhau: trục hoành Ox và trục tung Oy; giao điểm hai trục O là gốc tọa độ.

Trên mặt phẳng tọa độ, mỗi điểm M xác định một cặp số $\left(x_0;y_0\right)$; ngược lại mỗi cặp số $\left(x_0;y_0\right)$ xác định một điểm M. Cặp số $\left(x_0;y_0\right)$ gọi là tọa độ của điểm M; $x_0$ là hoành độ, $y_0$ là tung độ của điểm M. Ta viết $M\left(x_0;y_0\right)$.

4. Đồ thị của hàm số $y=f\left(x\right)$ là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng $\left(x;y\right)$ trên mặt phẳng tọa độ. $\left(x;y\right)$

5. Đồ thị của hàm số $y=ax\left(a\ne 0\right)$ là một đường thẳng đi qua gốc tọa độ.

6. Đồ thị hàm số $y=\frac{a}{x}\left(a;x\ne 0\right)$ là hai nhánh (hai đường cong), một nhánh nằm ở góc phần tư thứ I và một nhánh nằm ở góc phần tư thứ III khi $a>0$ và một nhánh nằm ở góc phần tư thứ II và một nhánh nằm ở góc phần tư thứ IV khi $a<0$.

B. Một số ví dụ

Ví dụ 1: Cho các cặp số  sau:

$\left(-2;-3\right);\left(-1,5;-4\right);\left(1,2;5\right);\left(\frac{5}{7};8\frac{2}{5}\right);\left(18;\frac{1}{3}\right);\left(-3;-2\right)$.

a) Lập bảng giá trị các cặp số.

b) Vẽ sơ đồ mũi tên.

c) Giải thích tại sao bảng vừa lập xác định y là một hàm số của x?

d) Hàm số đó có thể được cho bởi công thức nào?

P Tìm cách giải: Ta cần kiểm tra xem mỗi giá trị của đại lượng x có được tương ứng với một và chỉ một giá trị của đại lương y. Từ quan hệ của x và y viết công thức của hàm số.

Giải

a) Bảng giá trị các cặp số:

b) Sơ đồ mũi tên:

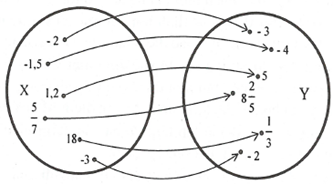
c) Trong bảng trên ta thấy mỗi giá trị của x đều được tương ứng $-xy=f\left(x\right)$ g với một và chỉ một giá trị của y là hàm số của x (việc lập bảng và sơ đồ mũi tên cũng đã chứng tỏ điều ấy).

d) Hàm số có thể được cho bởi công thức $y=\frac{6}{x}$ với $x\in \left\{-2;-1,5;1,2;\frac{5}{7};18;-3\right\}$

Ví dụ 2: Cho hàm số  được xác định bởi công thức $f\left(x\right)=-5x^2+6$

a) Tính $f\left(3\right);f\left(-3\right);f\left(-\frac{1}{3}\right);$

b) Tìm x để $f\left(x\right)=-74;f\left(x\right)=1;$

c) Chứng tỏ với $x\in R$ thì $f\left(x\right)=f\left(-x\right)$.