Phương pháp giải Sự tương giao giữa hai đồ thị hàm số 2024 (lý thuyết và bài tập)

Hoài Phạm Thị Thu Ngày: 25-10-2024 Lớp 12

Tải xuống 74 3.9 K 36

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Sự tương giao giữa hai đồ thị hàm số Toán lớp 12, tài liệu bao gồm 74 trang, tuyển chọn 217 bài tập Sự tương giao giữa hai đồ thị hàm số đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ HÀM SỐ

A. LÝ THUYẾT

1. Khái niệm tương giao.

Cho hàm số y = f (x) có đồ thị (C₁) và y = g (x) có đồ thị (C₂)

Phương trình hoành độ giao điểm của (C₁) và (C₂) là:

$f (x) = g (x)$ (1)

Khi đó:

Số giao điểm của (C₁) và (C₂) bằng với số nghiệm của phương trình (1).

Nghiệm x₀của phương trình (1) chính là hoành độ x₀của giao điểm.

Để tính tung độ y₀của giao điểm, ta thay hoành độ x₀vào y = f (x) hoặc y = g (x)

Điểm M(x₀;y₀) là giao điểm của (C₁) và (C₂)

2. Ví dụ minh họa:

Ví dụ 1. Biết đường thẳng $y = - \frac{9}{4} x - \frac{1}{24}$ cắt đồ thị hàm số $y = \frac{x^{3}}{3} + \frac{x^{2}}{2} - 2 x$ tại một điểm duy nhất, ký hiệu (x₀;y₀) là tọa độ điểm đó. Tìm y₀

_{A. $y_{0} = \frac{13}{12}$ B. $y_{0} = \frac{12}{13}$ C. $y_{0} = - \frac{1}{2}$ D. $y_{0} = - 2$}

Lời giải

..........................................................................................................................................................................................
.............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Ví dụ 2. Gọi M , N là giao điểm của đường thẳng (d): y = x - 1 và đường cong $(C) : y = \frac{2 x - 1}{x + 5}$ .Hoành độ trung

điểm I của đoạn thẳng MN bằng

A.1. B.2 . C. -1. D. -2 .

Lời giải

B. BÀI TẬP VỀ SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ HÀM SỐ

Bài 1. Tiếp tuyến của đồ thị hàm số 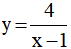100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) tại điểm có hoành độ x₀ = 2 có phương trình là:

A. y = -2x - 2

B. y = -4x + 12

C. y = x -1

D. y = -2x + 2

Bài 2. Cho hàm số y = x³ + x²- 6x+ 1. Phương trình tiếp tuyến tại điểm A(0; 1)

A. y = -2x+ 1

B. y = 2x+ 1

C. y = - 6x+ 1

D. y = 3x+ 1

Bài 3. Cho hàm số y = 2x² + 4x+ 1. Tiếp tuyến của đồ thị hàm số tại điểm có tung độ -1 có phương trình là

A. y = x+ 1

B.y = x

C. y = 1

D. y = -1

Bài 4. Cho đồ thị (C) của hàm số y = x³ + 6x² – 12x+ 1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm uốn.

A. y = - 24 x- 7

B. y = 10 x+ 2

C. y = 24 x + 1

D. Đáp án khác

Bài 5. Cho đồ thị của hàm số (C) 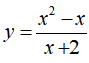100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1.

100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản)

Bài 6. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số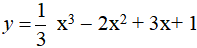 100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) có phương trình là:

A. y = 1

B. y = 0

C. y = x+ 1

D. y = x - 1

Bài 7. Cho hàm số 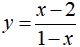100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:

A. y = - x + 1

B. y = - x+ 2

C. y = - 2x + 4

D. y = x - 2

Bài 8. Hệ số góc của tiếp tuyến của đồ thì hàm số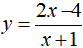 100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) tại giao điểm của đồ thị hàm số với trục tung bằng.

A. -2

B. 2

C. 6

D. 3

Bài 9. Phương trình tiếp tuyến của đồ thị hàm số 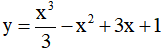100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) có hệ số góc k = 3 là

100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản)

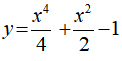
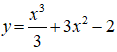
Bài 10. Hệ số góc của tiếp tuyến của đồ thị hàm số 100 Bài tập Sự tương giao của đồ thị hàm số có lời giải (cơ bản) tại điểm có hoành độ x₀ = 1 bằng: