Tính giá trị của biểu thức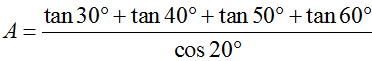 
bằng :
Giải bởi Vietjack
Chọn D.
Ta có:
Hệ quả
1) sinα và cosα xác định với mọi α ∈ R. Hơn nữa, ta có
sin(α + k2π) = sin α, ∀k ∈ Z;
cos(α + k2π) = cos α, ∀k ∈ Z
2) Vì –1 ≤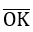 
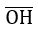
≤ 1; –1 ≤ 
≤ 1 nên ta có
–1 ≤ sin α ≤ 1
–1 ≤ cos α ≤ 1
3) Với mọi m ∈ R mà –1 ≤ m ≤ 1 đều tồn tại α và β sao cho sin α = m và cos β = m.
4) tanα xác định với mọi α ≠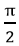 
+ kπ (k ∈ Z)
5) cotα xác định với mọi α ≠ kπ (k ∈ Z)
6) Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung = α trên đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
| Giá trị lượng giác |Góc phần tư | I | II | III | IV |
| cos α | + | - | - | + |
| sin α | + | + | - | - |
| tan α | + | - | + | - |
| cot α | + | - | + | - |
Xem thêm một số kiến thức liên quan:
Cho góc α thỏa mãn tanα = 2 và 1800< α < 2700 . Tính P = cosα + sinα
Cho hai góc nhọn a và b với tan a = 1/7 và tan b = 3/4. Tính tổng 2 góc đó?
Cho x và y là các góc nhọn, cotx = 3/4, cot y = 1/7. Tổng 2 góc đó là:
Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x) có giá trị không đổi và bằng
Cho A; B: C là ba góc của một tam giác không vuông. Hệ thức nào sau đây sai?
Cho A ; B; C là ba góc của một tam giác . Hãy chỉ ra hệ thức sai
Rút gọn biểu thức A = cos2( x - a) + cos2x - 2cos a.cos x.cos( a - x).
Cho A; B; C là ba góc của một tam giác. Hãy chỉ ra hệ thức sai
Cho biểu thức: A = sin2(a + b) – sin2a - sin2b. Đưa biểu thức trên về dạng tích:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
