Cho góc α thỏa mãn: 3cosα+ 2sinα = 2  và sinα < 0. Tính sinα

Chọn A.

Ta có 3cosα+ 2sinα = 2  hay (3cosα+ 2sinα = 2 )² = 4

Tương đương: 9 cos² α + 12 cosα .sin α + 4sin²α = 4

Hay 5cos²α +  12 cosα .sin α = 0

Từ đó: cosα= 0 hoặc 5cosα + 12 sinα = 0

+ Nếu cosα = 0 thì sinα =1: loại ( vì sinα < 0).

+ 5cosα + 12 sinα = 0 

ta có hệ phương trình 

SỐ ĐO CỦA CUNG VÀ GÓC LƯỢNG GIÁC

1. Độ và radian

a) Đơn vị radian

Trên đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số đo 1 rad.

b) Quan hệ giữa độ và radian

c) Độ dài của một cung tròn

Trên đường tròn bán kính R, cung nửa đường tròn có số đo là π rad và có độ dài là πR. Vậy cung có số đo α rad của đường tròn bán kính R có độ dài

l = Rα.

2. Số đo của một cung lượng giác

Số đo của một cung lượng giác 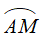 (A ≠ M) là một số thực âm hay dương.

Kí hiệu số đo của cung 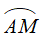 là sđ .

Ghi nhớ

Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của 2π.

Ta viết

sđ 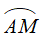 = α + k2π , k ∈ Z

trong đó α là số đo của một cung lượng giác tùy ý có điểm đầu là A, điểm cuối là M

3. Số đo của một góc lượng giác

Số đo của góc lượng giác (OA, OC) là số đo của cung lượng giác 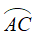 tương ứng.

Chú ý Vì mỗi cung lượng giác ứng với một góc lượng giác và ngược lại, đồng thời số đo của các cung và góc lượng giác tương ứng là trùng nhau, nên từ nay về sau khi ta nói về cung thì điều đó cũng đúng cho góc và ngược lại.

4. Biểu diễn cung lượng giác trên đường tròn lượng giác

Chọn điểm gốc A(1; 0) làm điểm đầu của tất cả các cung lượng giác trên đường tròn lượng giác. Để biểu diễn cung lượng giác có số đo α trên đường tròn lượng giác ta cần chọn điểm cuối M của cung này. Điểm cuối M được xác định bởi hệ thức sđ 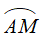 = α

Xem thêm một số kiến thức liên quan:

315 bài tập trắc nghiệm cung và góc lượng giác, công thức lượng giác

Tổng hợp lí thuyết và bài tập hay về Cung và góc lượng giác có giải chi tiết