Đề cương ôn tập cung và góc lượng giác

Quang Trung Ngày: 08-03-2024 Lớp 10

Tải xuống 12 1.4 K 9

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đề cương ôn tập cung và góc lượng giác, tài liệu bao gồm 12 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Đề cương ôn tập cung và góc lượng giác

Chương VI. Lượng giác

Đề cương ôn tập chương VI

A. Lý thuyết cần nhớ

1. Công thức cơ bản.

( ${\sin ^2}x + {\cos ^2}x = 1$, suy ra: ${\sin ^2}x = 1 - {\cos ^2}x$ và ${\cos ^2}x = 1 - {\sin ^2}x$;

( $1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}$, suy ra: ${\cos ^2}x = \frac{1}{{1 + {{\tan }^2}x}}$

( $1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}$, suy ra: ${\sin ^2}x = \frac{1}{{1 + {{\cot }^2}x}}$

$\Theta \tan x = \frac{{\sin x}}{{\cos x}};\cot x = \frac{{\cos x}}{{\sin x}};\tan x \cdot \cot x = 1.$

2. Công thức cộng. (Dùng để tách góc, hoặc ghép góc)

$\Theta \sin (a + b) = \sin a\cos b + \sin b\cos a$

(v) $\cos (a - b) = \cos a\cos b + \sin a\sin b$.

$\Theta \sin (a - b) = \sin a\cos b - \sin b\cos a$.

$ \odot \tan (a + b) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}$.

( $\cos (a + b) = \cos a\cos b - \sin a\sin b$.

$\Theta \tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}$.

3. Công thức góc nhân đôi. (Dùng để giảm góc)

$\Theta \sin 2\alpha = 2\sin \alpha \cos \alpha $.

(v) $\cos 2\alpha = 2{\cos ^2}\alpha - 1 = 1 - 2{\sin ^2}\alpha $

$\Theta \cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha .$

$\Theta \tan 2\alpha = \frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }}$.

4. Công thức hạ bậc. (Dùng để làm mất bình phương)

$ \odot {\sin ^2}\alpha = \frac{{1 - \cos 2\alpha }}{2}$.

$ \odot {\cos ^2}\alpha = \frac{{1 + \cos 2\alpha }}{2}.$

$ \odot {\tan ^2}\alpha = \frac{{1 - \cos 2\alpha }}{{1 + \cos 2\alpha }},\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.$

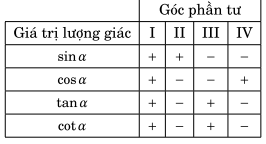
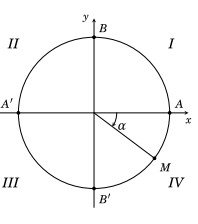
5. Dấu của các tỉ số lương giác tương ứng trên các góc phần tư.

Để xác định dấu của các giá trị lượng giác của một góc $\alpha $ ta xác định vị trí điểm cuối của cung $AM = \alpha $ trên đường tròn lượng giác. Điểm M thuộc góc phần tư nào thì ta áp dụng bảng xác định dấu của các giá trị lượng giác.

Đề cương ôn tập cung và góc lượng giác (ảnh 1)

Đề cương ôn tập cung và góc lượng giác (ảnh 2)

B. Các dạng toán tự luận

Dạng 1. Cho trước 1 tỉ số lượng giác, tính các tỉ số lượng giác còn lại

1. Ta thực hiện theo các bước:

Sử dụng công thức thích hợp để tính tỉ số tiếp theo (chú ý nhóm công thức cơ bản);

Ứng với miền của $\alpha $ đề cho, xem Mục 5 . để chọn kết quả đúng.

Tính toán các tỉ số còn lại.

2. Nếu đề cho trước 1 tỉ số lượng giác, yêu cầu tính giá trị biểu thức. Ta thường biến đổi biểu thức đó về giá trị đã cho. Sau đó, thay kết quả.

Ví dụ minh họa

Ví dụ 1

Biết $\sin \alpha = \frac{1}{3}$ và $\alpha \in \left( {\frac{\pi }{2};\pi } \right)$. Tính giá trị của $\cos \alpha ;\tan \alpha $ và $\cot \alpha $.

Lời giải.

Từ ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$ nên

${\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - \frac{1}{9} = \frac{8}{9} \Rightarrow \cos \alpha = \pm \frac{{2\sqrt 2 }}{3}$.

$\Theta $ $\alpha \in \left( {\frac{\pi }{2};\pi } \right)$ nên $\cos \alpha < 0$. Suy ra $\cos \alpha = - \frac{{2\sqrt 2 }}{3}$.

$\Theta \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \frac{1}{{2\sqrt 2 }};\cot \alpha = \frac{1}{{\tan \alpha }} = - 2\sqrt 2 $.

Ví dụ 2

Cho $\cos \alpha = \frac{3}{5}$, với $\alpha \in \left( {\frac{{3\pi }}{2};2\pi } \right)$. Tính giá trị của $\sin 2\alpha $ và $\tan 2\alpha $.

Lời giải.

Ta có

${\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha = \frac{{16}}{{25}} \Rightarrow \sin \alpha = \pm \frac{4}{5}$

$\Theta $ Do $\alpha \in \left( {\frac{{3\pi }}{2};2\pi } \right)$ nên $\sin \alpha < 0 \Rightarrow \sin \alpha = - \frac{4}{5}$

$\Theta \sin 2\alpha = 2\sin \alpha \cos \alpha = 2 \cdot \frac{3}{5} \cdot \frac{{ - 4}}{5} = \frac{{ - 24}}{{25}}$

$\Theta \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \frac{3}{4} \Rightarrow \tan 2\alpha = \frac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = - \frac{{24}}{7}$

Ví dụ 3

Cho $\tan \alpha = - \frac{3}{4}$, với $\frac{\pi }{2} < \alpha < \pi $. Tính giá trị của $\sin \alpha ,\sin 2\alpha $ và $\cos 2\alpha $.

Lời giải.

Ta có $\frac{1}{{{{\cos }^2}\alpha }} = 1 + {\tan ^2}\alpha = 1 + \frac{9}{{16}} = \frac{{25}}{{16}} \Rightarrow {\cos ^2}\alpha = \frac{{16}}{{25}}$

$ \odot {\sin ^2}\alpha = 1 - {\cos ^2}\alpha = \frac{9}{{25}} \Rightarrow \sin \alpha = \pm \frac{3}{5}$.

๑ Do $\frac{\pi }{2} < \alpha < \pi $ nên $\sin \alpha > 0$, do đó $\sin \alpha = \frac{3}{5}$.

๑Do $\frac{\pi }{2} < \alpha < \pi $ nên $\cos \alpha < 0$, do đó $\cos \alpha = - \frac{4}{5}$.

- $\sin 2\alpha = 2\sin \alpha \cos \alpha = - \frac{{24}}{{25}}$

- $\cos 2\alpha = 2{\cos ^2}\alpha - 1 = \frac{7}{{25}}$

Ví dụ 4

Cho $\sin \alpha = \frac{3}{5}$ với $\frac{\pi }{2} < \alpha < \pi $. Tính giá trị của biểu thức

$P = \cos \left( {\frac{{9\pi }}{2} - \alpha } \right) + 2\tan \left( {\alpha + \frac{{3\pi }}{2}} \right).$

Lời giải.

Áp dụng công thức cộng, ta có

$P = \cos \frac{{9\pi }}{2} \cdot \cos \alpha + \sin \frac{{9\pi }}{2} \cdot \sin \alpha = \sin \alpha - 2\cot \alpha $.

$\Theta {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = \frac{{16}}{{25}} \Rightarrow \cos \alpha = \pm \frac{4}{5}$

$\Theta $ Do $\frac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha = - \frac{4}{5}$ và $\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = - \frac{4}{3}$

$\Theta $ Suy ra, $P = \sin \alpha - 2\cot \alpha = \frac{{49}}{{15}}$.

Ví dụ 5

Cho $\tan \alpha = 3$. Tính giá trị biểu thức $B = \frac{{\sin \alpha - \cos \alpha }}{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha + 2\sin \alpha }}$.

Lời giải.

Ta biến đổi biểu thức $B$ về $\tan \alpha $ như sau:

$\begin{array}{l}B = \frac{{\frac{{\sin \alpha }}{{{{\cos }^3}\alpha }} - \frac{{\cos \alpha }}{{{{\cos }^3}\alpha }}}}{{\frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} + \frac{{3{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }} + \frac{{2\sin \alpha }}{{{{\cos }^3}\alpha }}}}\\ = \frac{{\tan \alpha \left( {{{\tan }^2}\alpha + 1} \right) - \left( {{{\tan }^2}\alpha + 1} \right)}}{{{{\tan }^3}\alpha + 3 + 2\tan \alpha \left( {{{\tan }^2}\alpha + 1} \right)}}\\ = \frac{{3(9 + 1) - (9 + 1)}}{{27 + 3 + 2.3(9 + 1)}} = \frac{2}{9}{\rm{. }}\left( {} \right)\end{array}$

Luyện tập 1

Bài 1. Cho $\cos \alpha = - \frac{{12}}{{13}}$ và $\frac{\pi }{2} < \alpha < \pi $. Tính $\sin \alpha $ và $\tan \alpha $.

Bài 2. Tính các giá trị lượng giác còn lại của góc $\alpha $, biết

a) $\sin \alpha = \frac{1}{3}$ và $90^{°} < α < 180^{°}$ ;

b) $\cos \alpha = - \frac{2}{3}$ và $\pi < \alpha < \frac{{3\pi }}{2}$.

Bài 3. Tính các giá trị lượng giác còn lại của góc $\alpha $, biết

a) $\tan \alpha = 2$ và $\pi < \alpha < 2\pi $;

b) $\cos \alpha = 0,8$ và $\tan \alpha + \cot \alpha > 0$.

Bài 4. Cho $\sin \alpha = \frac{{12}}{{13}}$ và $\frac{\pi }{2} \le \alpha \le \pi $. Tính các giá trị lượng giác còn lại của góc $\alpha $.

Bài 5. Cho $\tan \alpha = 3$ và $\alpha \in \left( {\pi ;\frac{{3\pi }}{2}} \right)$. Tính các giá trị lượng giác còn lại của góc $\alpha $.

Bài 6. Cho $\sin \alpha = - \frac{3}{5}$ và $\frac{{3\pi }}{2} < \alpha < 2\pi $. Tính $\cos \alpha ,\tan \alpha $; $\cos 2\alpha $ và $\sin \left( {\alpha + \frac{{19\pi }}{4}} \right)$.

Bài 7. Cho $\tan \alpha = - 2$ và $\frac{\pi }{2} < \alpha < \pi $. Tính $\cos \alpha ,\cos \left( {\alpha - \frac{{3\pi }}{4}} \right)$; $\cot \alpha $ và $\tan 2\alpha $.

Bài 8. Cho $\cos \alpha = \frac{2}{3}$ và $\frac{{3\pi }}{2} \le \alpha \le 2\pi $.

a) Tính $\tan \alpha ,\sin 2\alpha ,\tan 2\alpha $.

b) Tính $A = \frac{{9{{\sin }^2}\alpha + \sqrt 5 \cdot \tan \alpha }}{{5 + 6\cos \alpha }}$

c) Tính $\sin 2\alpha ,\cos 2\alpha ,\tan 2\alpha ,\cot 2\alpha $.

d) Tính $\sin \left( {\alpha + \frac{\pi }{4}} \right)$ và $\cos \left( {\frac{\pi }{3} - \alpha } \right)$.

Bài 9. Cho $0 \le \alpha \le \frac{\pi }{2}$. Xác định dấu của các giá trị lượng giác sau:

a) $\sin \left( {\alpha + \frac{\pi }{4}} \right)$

b) $\cos \left( {\alpha - \frac{\pi }{2}} \right)$

c) $\tan ( - \alpha )$.

Bài 10. Cho $\tan \alpha = 2$, tính giá trị biểu thức $M = {\cos ^2}\alpha - {\sin ^2}\alpha $.

Bài 11. Cho $\cot \alpha = 3$. Tính giá trị biểu thức $M = \frac{{2\sin \alpha - 3\cos \alpha }}{{5{{\sin }^3}\alpha + {{\cos }^3}\alpha }}$.

Bài 12. Cho $\cos \alpha = \frac{2}{3}$. Tính giá trị biểu thức $A = \frac{{\tan \alpha + 3\cot \alpha }}{{\tan \alpha + \cot \alpha }}$.

Bài 13. Cho $\sin x + \cos x = \frac{1}{2}$ và $\frac{\pi }{4} \le x \le \frac{\pi }{2}$. Tính $\sin 2x$ và $\cos 2x$.

Dạng 2. Rút gọn biểu thức hoạcc chứng minh đẳng thức

1. Các phương pháp thường dùng:

๑ Biến đổi vế phức tạp của đẳng thức về vế đơn giản;

$\Theta $ Biến đổi tương đương để đẳng thức đi đến kết quả hiển nhiên đúng;

๑ Phối hợp cả hai cách trên.

2. Chú ý:

$ \odot $ Nếu trong đẳng thức, các góc đều giống nhau, ta ưu tiên nhóm công thức cơ bản (Nhóm 1);

๑ Nếu trong đẳng thức, có xuất hiện góc gấp đôi và bình phương tỉ số lượng giác, ta ưu tiên nhóm nhân đôi và hạ bậc (Nhóm 3,4);

๑ Nếu cần tách góc, ta ưu tiên nhóm công thức cộng (Nhóm 2).

Ví dụ minh họa

Ví dụ 1

Rút gọn biểu thức:

a) $A = {\sin ^2}x + {\sin ^2}x{\tan ^2}x$

b) $B = \frac{{2{{\sin }^2}x - 1}}{{{{\sin }^2}x - \sin x\cos x}}$.

c) $A = {\cos ^2}\alpha \left( {{{\sin }^2}\alpha + 1} \right) + $ ${\sin ^4}\alpha $

Lời giải.

$\begin{array}{l}A = {\sin ^2}x + {\sin ^2}x{\tan ^2}x = {\sin ^2}x\left( {1 + {{\tan }^2}x} \right)\\ = {\sin ^2}x \cdot \frac{1}{{{{\cos }^2}x}} = {\tan ^2}x\end{array}$.

$\begin{array}{l}B = \frac{{2{{\sin }^2}x - 1}}{{{{\sin }^2}x - \sin x\cos x}} = \frac{{2{{\sin }^2}x - \left( {{{\sin }^2}x + {{\cos }^2}x} \right)}}{{\sin x(\sin x - \cos x)}}\\ = \frac{{\sin x + \cos x}}{{\sin x}} = 1 + \cot x\end{array}$;

$\begin{array}{l}A = {\sin ^2}\alpha \left( {1 - {{\sin }^2}\alpha } \right) + {\cos ^2}\alpha + {\sin ^4}\alpha \\ = {\sin ^2}\alpha - {\sin ^4}\alpha + {\cos ^2}\alpha + {\sin ^4}\alpha = 1\end{array}$.

Ví dụ. 2

Rút gọn các biểu thức:

a) $A = \frac{{\sqrt 2 \cos a - 2\cos \left( {\frac{\pi }{4} + a} \right)}}{{ - \sqrt 2 \sin a + 2\sin \left( {\frac{\pi }{4} + a} \right)}}.$

b) $B = (\tan a - \tan b)\cot (a - b) - \tan a\tan b$.

Lời giải.

a) Ta có

$\begin{array}{l}A = \frac{{\sqrt 2 \cos a - 2\left( {\cos \frac{\pi }{4}\cos a - \sin \frac{\pi }{4}\sin a} \right)}}{{ - \sqrt 2 \sin a + 2\left( {\sin \frac{\pi }{4}\cos a + \cos \frac{\pi }{4}\sin a} \right)}}\\ = \frac{{\sqrt 2 \sin a}}{{\sqrt 2 \cos a}} = \tan a\end{array}$.

b) Ta có $B = \tan (a - b)(1 + \tan a\tan b)\cot (a - b) - \tan a\tan b = 1$.

Xem thêm